Эллипс и его уравнения

Элементы эллипса

Чтобы полностью понять формирование эллипса, необходимо знать каждый его элемент. Это фокусы, центр, большая ось и малая ось. По ним можно проследить важные взаимосвязи в эллипсе.

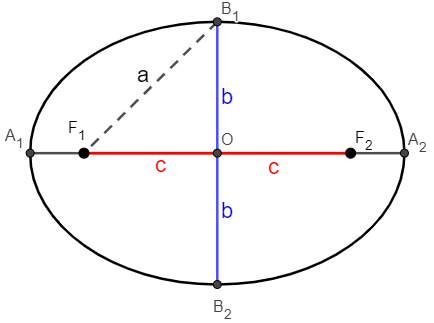
• Центр эллипса представлен точкой O.

• Уже F баллов₁ и F₂ представляют собой фокусы эллипса.

• точки A₁ и₂ являются концами горизонтальной оси эллипса, а точки B₁ и B₂ являются концами его вертикальной оси.

• Расстояние между B₁ и B₂ равна 2b (длина эллипса на малой оси).

• Расстояние между A₁ и₂ равна 2a (длина эллипса на большой оси).

• Фокусное расстояние между F₁ и F₂ равно 2c.

Наблюдение: Важно понимать, что F1B1 имеет длину, равную половине горизонтальной оси, то есть dF1B1 = а. Таким образом, при анализе треугольника A также можно увидеть важную связь Пифагора.1OB1

Обратите внимание, что он прямоугольный треугольник. Следовательно, мы можем применить теорема Пифагора

a² = b² + c²

Есть еще одна возможность для эллипса, когда самая длинная ось является вертикальной осью. В этом случае элементы остаются прежними.

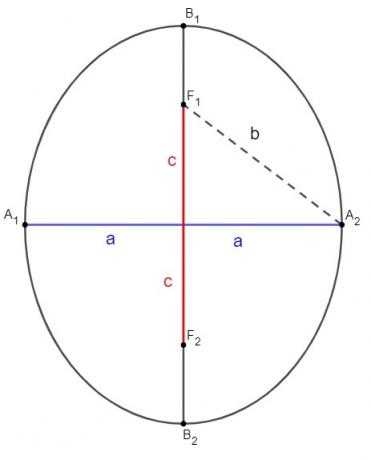
В этом случае мы также можем применить теорему Пифагора, получив следующее:

b² = a² + c²

Читайте тоже: Что такое элементы многоугольника?

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

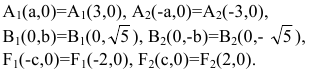
Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Соотношения между элементами эллипса[]

Файл:Ellipse parameters.gif

Части эллипса (описание см. в разделе «Связанные определения»)

•  a{\displaystyle ~{\boldsymbol {a}}} — большая полуось;
•  b{\displaystyle ~{\boldsymbol {b}}} — малая полуось;
•  c{\displaystyle ~{\boldsymbol {c}}} — фокальное расстояние (полурасстояние между фокусами);
•  p{\displaystyle ~{\boldsymbol {p}}} — фокальный параметр;
•  rp{\displaystyle ~{\boldsymbol {r}}_{p}} — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
•  ra{\displaystyle ~{\boldsymbol {r}}_{a}} — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);

 a2=b2+c2{\displaystyle ~a^{2}=b^{2}+c^{2}}

e=ca=1−b2a2(≤e<1).{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leq e<1).}.

 p=b2a{\displaystyle ~p={\frac {b^{2}}{a}}}

	a{\displaystyle ~{\boldsymbol {a}}}	b{\displaystyle ~{\boldsymbol {b}}}	c{\displaystyle ~{\boldsymbol {c}}}	p{\displaystyle ~{\boldsymbol {p}}}	rp{\displaystyle ~{\boldsymbol {r_{p}}}}	ra{\displaystyle ~{\boldsymbol {r_{a}}}}
a{\displaystyle ~{\boldsymbol {a}}} – большая полуось	a{\displaystyle ~{\boldsymbol {a}}}	a=b1−e2{\displaystyle ~a={\frac {b}{\sqrt {1-e^{2}}}}}	a=ce{\displaystyle ~a={\frac {c}{e}}}	a=p1−e2{\displaystyle ~a={\frac {p}{1-e^{2}}}}	a=rp1−e{\displaystyle ~a={\frac {r_{p}}{1-e}}}	a=ra1+e{\displaystyle ~a={\frac {r_{a}}{1+e}}}
b{\displaystyle ~{\boldsymbol {b}}} – малая полуось	b=a1−e2{\displaystyle ~b=a{\sqrt {1-e^{2}}}}	b{\displaystyle ~{\boldsymbol {b}}}	b=c 1−e2e{\displaystyle ~b={\frac {c~{\sqrt {1-e^{2}}}}{e}}}	b=p1−e2{\displaystyle ~b={\frac {p}{\sqrt {1-e^{2}}}}}	b=rp1+e1−e{\displaystyle ~b=r_{p}{\sqrt {\frac {1+e}{1-e}}}}	b=ra1−e1+e{\displaystyle ~b=r_{a}{\sqrt {\frac {1-e}{1+e}}}}
c{\displaystyle ~{\boldsymbol {c}}} – фокальное расстояние	c=ae{\displaystyle ~c=ae}	c=be1−e2{\displaystyle ~c={\frac {be}{\sqrt {1-e^{2}}}}}	c{\displaystyle ~{\boldsymbol {c}}}	c=pe1−e2{\displaystyle ~c={\frac {pe}{1-e^{2}}}}	c=rpe1−e{\displaystyle ~c={\frac {r_{p}e}{1-e}}}	c=rae1+e{\displaystyle ~c={\frac {r_{a}e}{1+e}}}
p{\displaystyle ~{\boldsymbol {p}}} – фокальный параметр	p=a(1−e2){\displaystyle ~p=a(1-e^{2})}	p=b 1−e2{\displaystyle ~p=b~{\sqrt {1-e^{2}}}}	p=c 1−e2e{\displaystyle ~p=c~{\frac {1-e^{2}}{e}}}	p{\displaystyle ~{\boldsymbol {p}}}	p=rp(1+e){\displaystyle ~p=r_{p}(1+e)}	p=ra(1−e){\displaystyle ~p=r_{a}(1-e)}
rp{\displaystyle ~{\boldsymbol {r}}_{p}} – перифокусное расстояние	rp=a(1−e){\displaystyle ~r_{p}=a(1-e)}	rp=b 1−e1+e{\displaystyle ~r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}}	rp=c 1−ee{\displaystyle ~r_{p}=c~{\frac {1-e}{e}}}	rp=p1+e{\displaystyle ~r_{p}={\frac {p}{1+e}}}	rp{\displaystyle ~{\boldsymbol {r}}_{p}}	rp=ra1−e1+e{\displaystyle ~r_{p}=r_{a}{\frac {1-e}{1+e}}}
ra{\displaystyle ~{\boldsymbol {r}}_{a}} – апофокусное расстояние	ra=a(1+e){\displaystyle ~r_{a}=a(1+e)}	ra=b 1+e1−e{\displaystyle ~r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}}	ra=c 1+ee{\displaystyle ~r_{a}=c~{\frac {1+e}{e}}}	ra=p1−e{\displaystyle ~r_{a}={\frac {p}{1-e}}}	ra=rp 1+e1−e{\displaystyle ~r_{a}=r_{p}~{\frac {1+e}{1-e}}}	ra{\displaystyle ~{\boldsymbol {r}}_{a}}

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

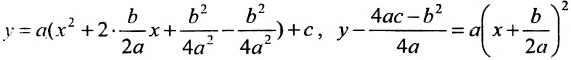
и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

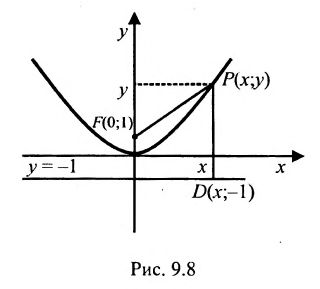
Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Уравнение эллипсоида

Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.

Рассмотрим сферу радиуса R с центром в начале координат:

где Х, У, Z — текущие координаты точки сферы.

Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными

В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем

Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.

Подставляя эти формулы в уравнение (1), будем иметь

где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.

Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).

Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями

а = b = 6377 км и с = 6356 км.

Если а = b = с, то эллипсоид превращается в сферу.

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Гипербола
• Парабола
• Многогранник
• Решение задач на вычисление площадей
• Шар в геометрии
• Правильные многогранники в геометрии
• Многогранники
• Окружность

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Уравнение касательной к эллипсу.

Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть \(M_{0}(x_{0}, y_{0})\) — точка на эллипсе и \(y_{0} \neq 0\). Через \(M_{0}\) проходит график некоторой функции \(y=f(x)\), который целиком лежит на эллипсе. (Для \(y_{0} > 0\) это график \(f_{1}(x)=b\sqrt{1-x^{2}/a^{2}}\), для \(y_{0} < 0\) — график \(f_{2}(x)=-b\sqrt{1-x^{2}/a^{2}}\). Не уточняя знака \(y_{0}\), обозначим подходящую функцию \(f(x)\).) Для нее выполнено тождество
$$
\frac{x^{2}}{a^{2}}+\frac{(f(x))^{2}}{b^{2}}=1.\nonumber
$$
Дифференцируем его по \(x\):
$$
\frac{2x}{a^{2}}+\frac{2ff’}{b^{2}}=0.\nonumber
$$
Подставляя \(x=x_{0}\) и \(f(x_{0}=y_{0})\), находим производную от \(f\) в точке \(x_{0}\), равную угловому коэффициенту касательной:
$$
f'(x_{0})=\frac{b^{2}}{a^{2}} \frac{x_{0}}{y_{0}}.\nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-\frac{b^{2}}{a^{2}} \frac{x_{0}}{y_{0}}(x-x_{0}).\nonumber
$$
Упрощая это уравнение, учтем, что \(b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}\), так как \(M_{0}\) лежит на эллипсе. Результату можно придать вид
$$
\frac{xx_{0}}{a^{2}}+\frac{yy_{0}}{b^{2}}=1.\label{ref8}
$$

При выводе уравнения \eqref{ref8} мы исключили вершины эллипса \((a, 0)\) и \((-a, 0)\), положив \(y_{0} \neq 0\). Для этих точек оно превращается, соответственно, в уравнения \(x=a\) и \(x=-a\). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение \eqref{ref8} определяет касательную для любой точки \(M_{0}(x_{0}, y_{0})\) на эллипсе.

Утверждение 5.

Касательная к эллипсу в точке \(M_{0}(x_{0}, y_{0})\) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Нам надо сравнить углы \(\varphi_{1}\) и \(\varphi_{2}\), составленные векторами \(\overrightarrow{F_{1}M_{0}}\) и \(\overrightarrow{F_{2}M_{0}}\) с вектором \(\boldsymbol{n}\), перпендикулярным касательной (рис. 8.5). Из уравнения \eqref{ref8} находим, что \(\boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})\), и потому
$$
(\overrightarrow{F_{1}M_{0}}, \boldsymbol{n})=\frac{x_{0}}{a^{2}}(x_{0}-c)+\frac{y_{0}}{b^{2}}y_{0}=1-\frac{x_{0}c}{a^{2}}=\frac{a-\varepsilon x_{0}}{a}.\nonumber
$$
Используя \eqref{ref4}, мы получаем отсюда, что \(\cos \varphi_{1}=1/(a|\boldsymbol{n}|)\). Аналогично находим \(\cos \varphi_{2}=1/(a|\boldsymbol{n}|)\). Утверждение доказано.

Рис. 8.5.

Эксцентриситет эллипса

Определение

Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается

Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:

 Рис. 3

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим – полуфокусное расстояние.

Строим фокусы и на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках  и . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Определение.

Пусть по определению
$$
c^{2}=a^{2}-b^{2}\label{ref2}
$$
и \(c \geq 0\).

Фокусами называются точки \(F_{1}\) и \(F_{2}\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности \(c=0\), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Определение.

Отношение
$$
\varepsilon=\frac{c}{a}\label{ref3}
$$
называется эксцентриситетом эллипса.

Отметим, что \(\varepsilon < 1\).

Утверждение 2.

Расстояние от произвольной точки \(M(x, y)\), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы \(x\):
$$
r_{1}=|F_{1}M|=a-\varepsilon x,\ r_{2}=|F_{2}M|=a+\varepsilon x.\label{ref4}
$$

Очевидно, что \(r_{1}^{2}=(x-c)^{2}+y^{2}\). Подставим сюда выражение для \(y^{2}\), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-\frac{b^{2}x^{2}}{a^{2}}.\nonumber
$$

Учитывая равенство \eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+\frac{c^{2}x^{2}}{a^{2}}=(a-\varepsilon x)^{2}.\nonumber
$$
Так как \(x \leq a\) и \(\varepsilon < 1\), отсюда следует, что справедливо первое из равенств \eqref{ref4}: \(r_{1}=a-\varepsilon x\). Второе равенство доказывается аналогично.

Утверждение 3.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса \(2a\).

Необходимость. Если мы сложим равенства \eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.\label{ref5}
$$Достаточность. Пусть для точки \(M(x, y)\) выполнено условие \eqref{ref5}, то есть
$$
\sqrt{(x-c)^{2}+y^{2}}=2a-\sqrt{(x+c)^{2}+y^{2}}.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=a\sqrt{(x+c)^{2}+y^{2}}.\label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref{ref2}. Мы придем к \(b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\), равносильному уравнению эллипса \eqref{ref1}.

С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=\frac{a}{\varepsilon},\\ x=-\frac{a}{\varepsilon}.\label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.

Рис. 8.4. Фокусы и директрисы эллипса.

Утверждение 4.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса \(\varepsilon\).

Докажем это предложение для фокуса \(F_{2}(-c, 0)\). Пусть \(M(x, y)\) — произвольная точка эллипса. Расстояние от \(M\) до директрисы с уравнением \(x=-a/\varepsilon\) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+\frac{a}{\varepsilon}|=\frac{1}{\varepsilon}(\varepsilon x+a).\nonumber
$$
Из формулы \eqref{ref4} мы видим теперь, что \(r_{2}/d_{2}=\varepsilon\).

Обратно, пусть для какой-то точки плоскости \(r_{2}/d_{2}=\varepsilon\), то есть
$$
\sqrt{(x+c)^{2}+y^{2}}=\varepsilon \left(x+\frac{a}{\varepsilon}\right).\nonumber
$$
Так как \(\varepsilon=c/a\), это равенство легко приводится к виду \eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.

Радиотелескоп СКА

Этот радиотелескоп является самым большим в своем роде и, как ожидается, начнет работать в 2021 году. Его площадь поверхности составляет 1 квадратный километр, поэтому он называется SKA (на английском языке это аббревиатура от Массив квадратных километров).

Воспользовавшись свойством отражения эллипсов, структура состоит из массива из 3000 антенн эллиптической формы шириной около 15 м, распределенных между Австралией и Южной Африкой. Можно надеяться, что с помощью этого инструмента, в 50 раз более чувствительного, чем те, которые используются сейчас, можно взглянуть на Вселенную, когда она была еще намного моложе: всего на миллиард лет.

Эллипс и его каноническое уравнение

Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».

Каноническое уравнение эллипса имеет вид , где   – положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:

Как построить эллипс?

Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:

Пример 1

Построить эллипс, заданный уравнением

Решение: сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения  заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае : Отрезок  называют большой осью эллипса; отрезок  – малой осью; число  называют большой полуосью эллипса; число  – малой полуосью. в нашем примере: .

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы. И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса  на черновике быстренько выражаем: 

Далее уравнение распадается на две функции: – определяет верхнюю дугу эллипса; – определяет нижнюю дугу эллипса.

Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами . Настукаем три смс-ки на калькуляторе: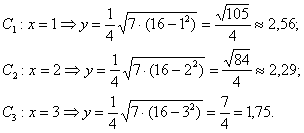 Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки  (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию: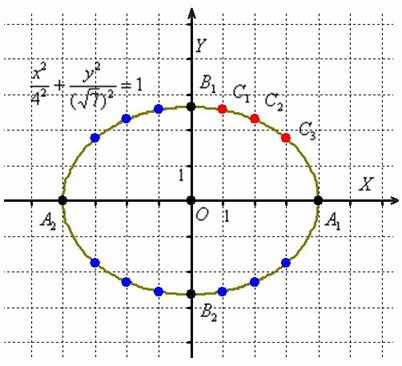 Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Кривые второго порядка — определение и построение с примерами решения

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Элементы эллипса

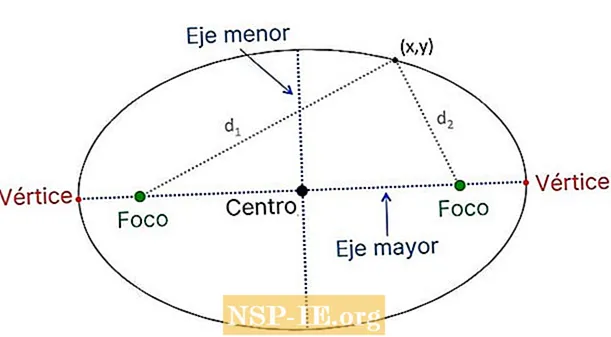
Основные элементы эллипса

Это основные элементы эллипса:

1. Прожекторы, неподвижные точки, расположенные на самой длинной оси эллипса.
2. Вершины, — две точки эллипса, через которые проходит линия, соединяющая фокусы.
3. Большая ось, — хорда, соединяющая вершины и содержащая фокусы.
4. Центр, середина большой оси, которая на рисунке соответствует координатной точке (h, k). Каждый фокус находится на одинаковом расстоянии от центра и на расстоянии c того же самого.
5. Малая ось, — хорда, проходящая через центр и перпендикулярная большой оси.
6. Радио векторы, сегменты, которые соединяют каждый фокус с точкой P на эллипсе.
7. Фокальная ось, прямая, на которой расположены очаги.
8. Фокусное расстояние, — расстояние между фокусами, обозначенное как 2c.
9. Вторичный вал, ось, перпендикулярная большой оси, которая также является посредником сегмента, соединяющего фокусы.
10. Центр симметрии, точка, совпадающая с центром эллипса, где пересекаются его оси симметрии.
11. Оси симметрии, линии, содержащие большую и малую оси эллипса.