Психология форм в дизайне ux

Линзы. Оптическая сила линзы

Линза – это прозрачное тело, ограниченное двумя сферическими или криволинейными поверхностями, одна из которых может быть плоской.

Тонкая линза – физическая модель линзы, в которой ее толщиной можно пренебречь по сравнению с диаметром линзы.

Классификация линз

1. По форме:

• выпуклые – это линзы, у которых средняя часть толще, чем края;
• вогнутые – это линзы, у которых края толще, чем средняя часть.

2. По оптическим свойствам:

собирающие – это линзы, после прохождения которых параллельный пучок лучей собирается в одной точке;

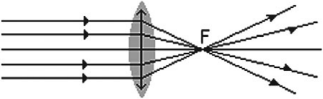
рассеивающие – это линзы, после прохождения которых параллельный пучок лучей рассеивается.

Условные обозначения:

Величины, характеризующие линзу

Главная оптическая ось – это прямая, проходящая через центры сферических поверхностей линзы.

Оптический центр линзы – это точка пересечения главной оптической оси с линзой, проходя через которую луч не изменяет своего направления.

Побочная оптическая ось – это любая прямая, проходящая через оптический центр линзы под произвольным углом к главной оптической оси.

Фокус линзы – это точка, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси.

Обозначение – ​\( F \)​.

Фокусное расстояние – это расстояние от оптического центра линзы до ее фокуса. Обозначение – \( F \), единица измерения – м.

Фокальная плоскость – это плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.

Побочный фокус – это точка пересечения побочной оптической оси с фокальной плоскостью.

Оптическая сила линзы – это величина, обратная фокусному расстоянию.

Обозначение – ​\( D \)​, единица измерения – диоптрия (дптр):

1 дптр – это оптическая сила линзы с фокусным расстоянием 1 м.

Важно!
Оптическая сила линзы зависит от показателя преломления линзы и от радиусов кривизны сферических поверхностей, ограничивающих линзу:

где ​\( n_л \)​ – показатель преломления линзы, ​\( n_{ср} \)​ – показатель преломления среды, ​\( R_1 \)​ и \( R_2 \) – радиусы сферических поверхностей.

Если поверхности выпуклые, то ​\( R_1 \)​ > 0 и \( R_2 \) > 0, если поверхности вогнутые, то \( R_1 \) < 0 и \( R_2 \) < 0.

Если одна из поверхностей линзы плоская, например первая, то ​\( R_1\to\infty \)​, а вторая поверхность выпуклая: \( R_2 \) > 0, то

Прямолинейное распространение света

Закон распространения света:
свет в прозрачной однородной среде распространяется прямолинейно.

Экспериментальным доказательством прямолинейности распространения света является образование тени.

Тень – это область пространства, куда не попадает свет от источника.

Полутень – это область пространства, куда частично попадает свет от источника.

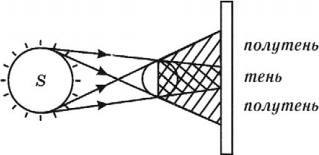
Если источник света точечный, то на экране образуется четкая тень предмета.

Если источник неточечный, то на экране образуется размытая тень (области тени и полутени).

Образованием тени при падении света на непрозрачный предмет объясняются такие явления, как солнечное и лунное затмения.

Современная оптика[]

Основные закономерности оптики

‎Электромагнитный спектр принято делить на радиоволны, инфракрасное, видимое, ультрафиолетовое, рентгеновское и гамма-излучения. Эти участки спектра различаются не по своей природе, а по способу генерации и приёма излучения. Поэтому между ними нет резких переходов, сами участки перекрываются, а границы между ними условны.

Волновые и квантовые закономерности являются общими для всего спектра электромагнитного излучения. В зависимости от длины волны, на первый план выступают разные явления, разные методы исследования и разные практические применения. Поэтому на оптику нельзя смотреть как на замкнутую дисциплину, изучающую только видимую область спектра, отделенную от других областей чёткими границами. Закономерности и результаты, найденные в этих других областях, могут оказаться применимыми в видимой области спектра и наоборот.

Современная оптика охватывает области оптической науки и разработок, которые стали популярными в 20-ом столетии. Эти области оптической науки в основном касаются электромагнитных или квантовых свойств света, но на самом деле включают другие области.

Рентгеновская оптика преломления

Основная статья: Рентгеновская оптика преломления

Линза из кремния для преломления Х-лучей

Единичная параболическая линза

Рентгеновская оптика преломления — оптика, отличаются новыми свойствами и характкристиками, обеспечивающая преломление и фокусировку Х-лучей аналогично тонким линзам на базе преломляющих линз, фокусирующих оптических элементов, на базе киноформных преломляющих профилей и оптических элементов призм, полученных из кремния.

Нанооптика

Наносреда из электромагнитно-двойных пар золотых точек

В наносозданной среде получен эффект взамодействия электромагнитных волн с сильным магнитным ответом в зоне видимого спектра электромагнитных волн («видимых-легких частот»), включая полосу с отрицательным магнетизмом. Среда сделана из электромагнитночувствительных двойных пар золотых точек с геометрией и симметрией, тщательно разработанной на нанометрическом уровне. Возникающий магнитный ответ величиной 600-700 ТГц (1012Гц) получается благодаря возбуждению антисимметричного плазменного резонанса. Высокочастотная проходимость проявляет себя качественно с новым эффектом оптического взаимодействия в данных наносредах. Это впервые показывает возможность применения электромагнетизма в зоне видимых частот и прокладывает путь в видимой оптике для получения оптических систем с лучшими показателями преломления, прозрачности к определённым лучам света.

Физиологическая оптика

Основная статья: Зрение

Основная статья: Бионический глаз

Глаз человека

Физиологическая оптика — наука о зрительном восприятии света глазами. Она объединяет сведения по биофизике, биохимии, биотехнологиям, психологии зрительного восприятия и др. В настоящее время выдающиеся достижения в области офтальматологии связаны с достижениями в биотехнологиях привело , например, в области создания фотосенсоров с матрицей на базе органических соединений, способных вживаться в атрофированную сетчатку глаза слепых и возвращать им зрение (См. Бионический глаз).

У истоков развития науки об оптике было Зрительное восприятие, зрение, строение глаза. Само название (от др.-греч. ὀπτική — в переводе оптика) определила область в физике под названием Оптика. Линза (биологическая)— не что иное как хрусталик глаза, сетчатка же глаза — основа появления светочувствительных фотоматериалов, глаз — это биологисеский фотоаппарат. Откуда направление в физике —Оптика закономерно изучает взаимодействие спектра видимых и примыкающих к ним электромагнитных лучей со средой и веществом.

Волоконная оптика

Основная статья: Волоконная оптика

Световод

Волоконная оптика — раздел оптики, который изучает физические явления, возникающие и протекающие в оптических волокнах, включая продукцию отраслей точного машиностроения на основе оптических волокон.

Волоконная оптика — сочетание прикладной науки и производства, востребованные проектом на основе применения оптических волокон.

Темы, связанные с современной оптикой

• Адаптивная оптика
• Круглый дихроизм
• Кристаллическая оптика
• Дифракция
• Волновод
• Голография
• Интегральная оптика
• Исчисление Джонса
• Лазер
• Микрооптика
• Неотображение оптики
• Нелинейная оптика
• Оптические методы моделирования
• Оптическое распознавание образов
• Оптический компьютер
• Оптический Вихрь
• Фотометрия
• Фотоника
• Квантовая оптика
• Радиометрия
• Статистическая оптика
• «Беспризорный» свет
• Оптика тонких плёнок
• Рентгеновская оптика преломления
• Рентгеновское зеркало
• Отражение рентгеновских лучей‎
• Бионическое зрение

Баланс

Ощущение гармонии в композиции может быть весьма субъективно. При этом есть некоторые правила баланса, которые работают для всех примерно одинаково.

Баланс в композиции заключается в расположении элементов таким образом, чтобы они были стабильны и устойчивы или, наоборот, обладали динамикой за счёт неуравновешенности. Значимость элемента могут формировать его размер, контраст, насыщенность и форма.

Симметрия

При симметричном балансе одна сторона изображения — зеркально отражённая копия другой. Получается, что на двух сторонах изображения по обе стороны от оси, проходящей через центр, находятся равные по значимости элементы.

Симметрия легко считывается, она понятна и вызывает чувство устойчивости. Однако часто подобные композиции слишком статичны и потому могут казаться скучными. Это происходит из-за того, что изображение предсказуемо — ведь обе его половины практически идентичны.

Логотип Shell симметричен и выглядит «простым»Изображение: Wikimedia Commons

Асимметричный баланс — следствие неравнозначности каждой из сторон композиции. Так, например, доминирующий элемент может быть только на одной стороне, а уравновешивать его будут пара или несколько менее значительных объектов на другой.

Асимметрия идеально подходит для минималистского дизайна. Она помогает создать динамику при минимуме деталей, поскольку во время движения глаз получает каждый раз новую информацию — переходит от более крупных элементов к более мелким или от тёмных оттенков к более светлым.

Логотип YouTube выглядит динамичным из-за асимметрииИзображение: Wikimedia Commons

Асимметрия всегда выглядит интереснее, поскольку в неё заложено больше визуального разнообразия. Однако она требует более серьёзной работы, ведь достичь баланса между отдельными элементами сложнее.

Радиальный баланс — это симметрия в нескольких направлениях. Элементы располагаются вокруг центральной точки композиции, как спицы велосипедного колеса. Часто радиально сбалансированные конструкции заключены в круг, но дизайнеры экспериментируют и с другими формами — квадратами, треугольниками, восьмиугольниками, звёздами. В такой композиции центральная точка становится главным местом притяжения.

В основе логотипа Mitsubishi — радиальный балансИзображение: Wikimedia Commons

Мозаичный баланс можно определить как организованный хаос. В композиции отсутствуют чёткие смысловые центры, а элементы имеют одинаковый по значимости «вес». Отсутствие иерархии должно приводить к, казалось бы, визуальному шуму, но равновесие сохраняется благодаря отсутствию чёткого фокуса внимания из-за равнозначности элементов.

Логотип Microsoft — пример мозаичного балансаИзображение: Wikimedia Commons

Сбалансированный дизайн всегда выглядит гармоничнее, потому что информация в нём организована, что помогает избегать напряжения из-за визуального хаоса.

Золотое сечение

Соотношение объектов, которое имеет наиболее приятные для восприятия пропорции формы или структуры, получило название золотого сечения.

Оно определяет отношение большей части к меньшей так же, как и большей к целому. Из-за этого его удобно применять для подбора размеров элементов. Древние греки вывели универсальное число этой пропорции — 1,68. Увеличивая элементы относительно друг друга согласно этому соотношению, можно получать гармоничные структуры.

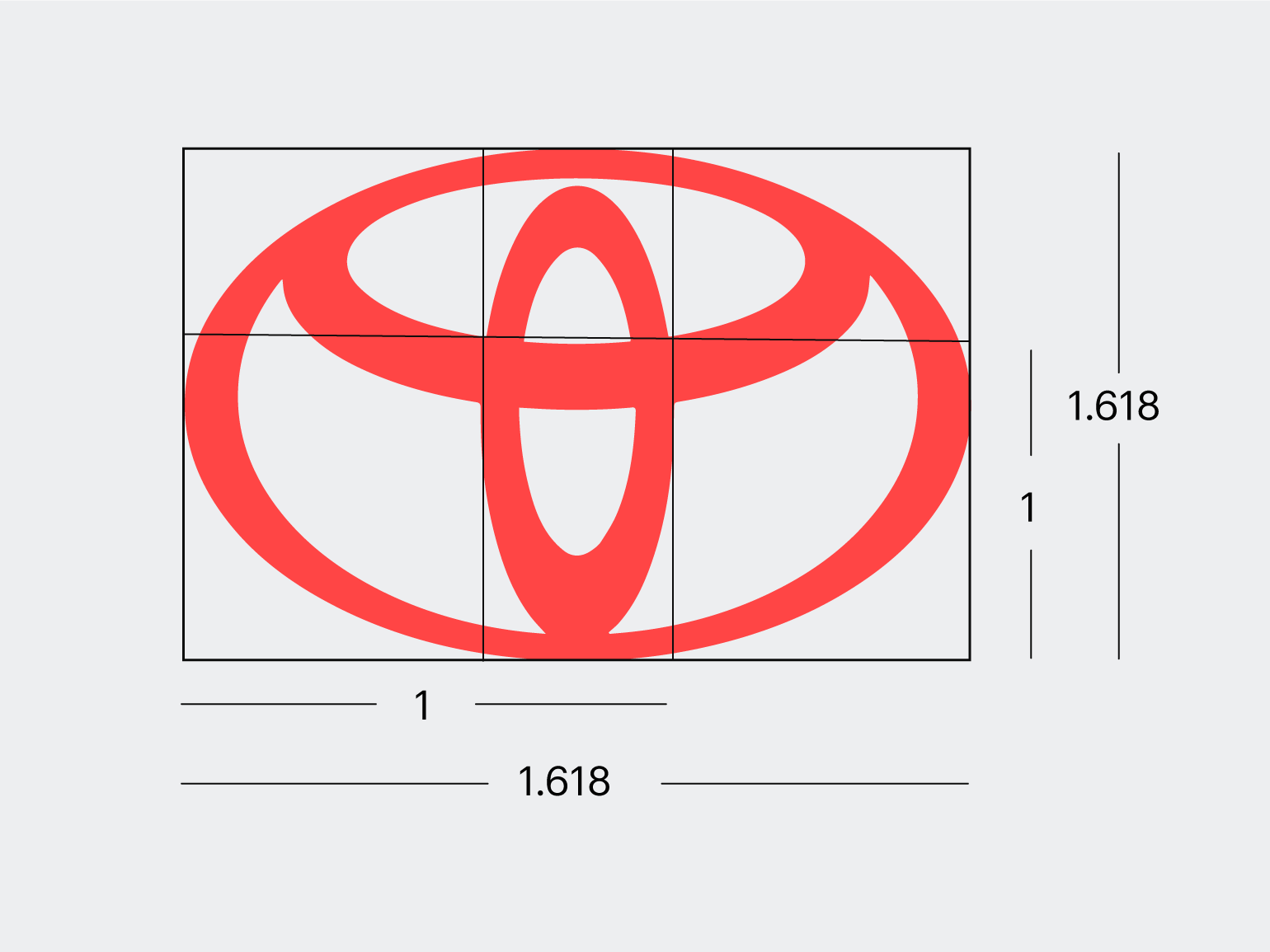
В логотипе Toyota использовано золотое сечениеИзображение: Polina Vari для Skillbox Media

Также для создания гармоничных композиций используется золотая спираль, организованная по принципу золотого сечения — на её линии располагают ключевые элементы.

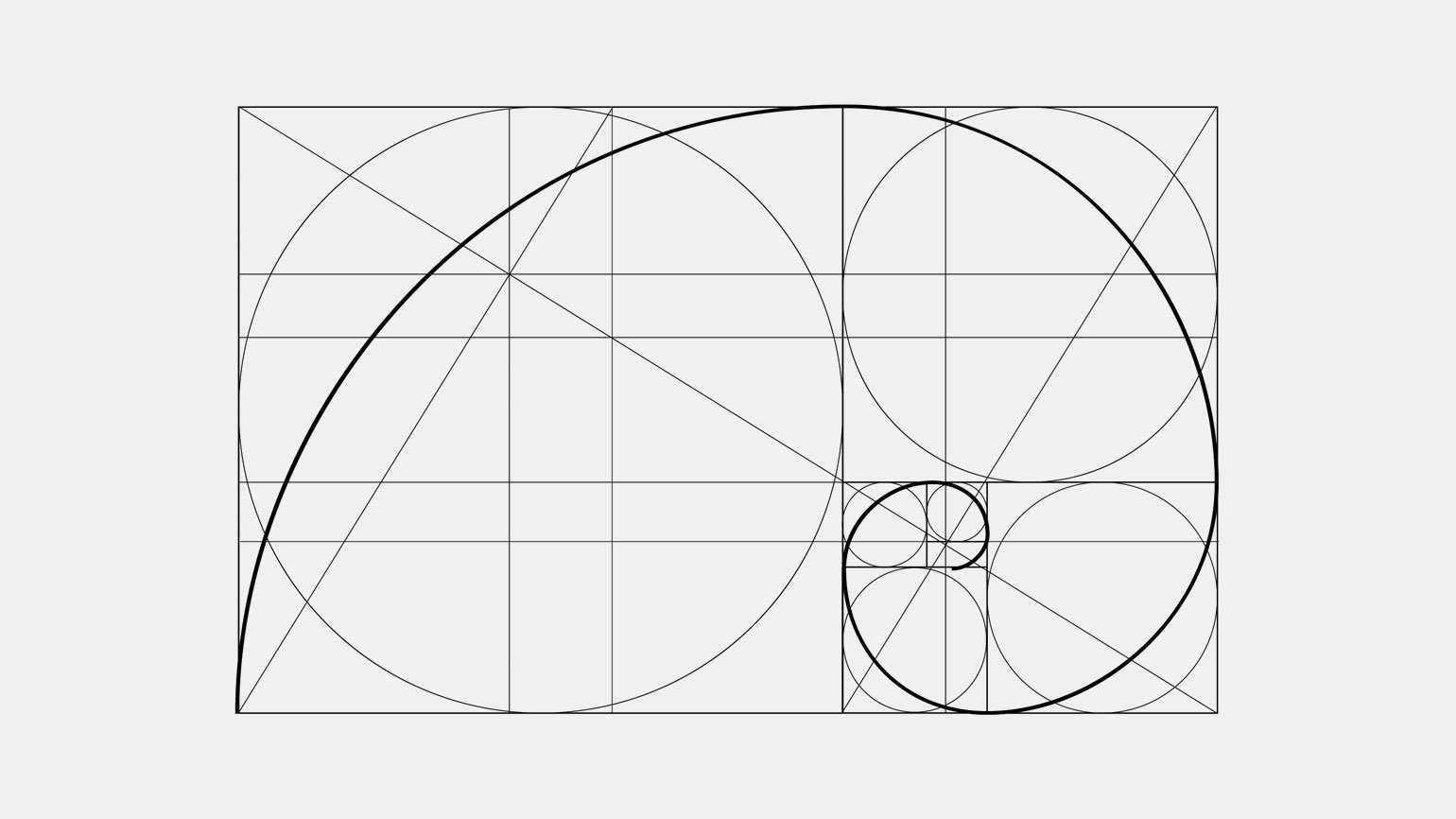
Построение золотой спиралиИзображение: Oleh Svetiukha / Shutterstock

Негативное и позитивное пространство

Важное значение имеют не только сами элементы, но и то пространство, которое их разделяет. Позитивным пространством называют те места, которые занимают сами элементы

Негативным — то пространство, которое находится между ними.

Негативное пространство имеет большое значение при группировке элементов, отделении главного от второстепенного. Оно же делает дизайн воздушным. Также с помощью незаполненных областей можно создавать оптические иллюзии, например добавлять скрытые элементы.

В логотипе компании FedEx, которая занимается почтовыми и курьерскими доставками, между буквами E и X спрятана стрелкаИзображение: Wikimedia Commons

Координатное представление[]

Каноническое уравнение

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

x2a2+y2b2=1.{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.}

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Для определённости положим, что <b⩽a.{\displaystyle 0<b\leqslant a.} В этом случае величины a{\displaystyle a} и b{\displaystyle b} — соответственно, большая и малая полуоси эллипса.

Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:

|F1F2|=2a2−b2,e=a2−b2a<1.{\displaystyle \left|F_{1}F_{2}\right|=2{\sqrt {a^{2}-b^{2}}},\;\;\;e={\frac {\sqrt {a^{2}-b^{2}}}{a}}<1.}

Координаты фокусов эллипса:

(ae,),(−ae,).{\displaystyle \left(ae,\,0\right),\;\;\;\left(-ae,\,0\right).}

Эллипс имеет две директрисы, уравнения которых можно записать как

x=ae,x=−ae.{\displaystyle x={\frac {a}{e}},\;\;\;x=-{\frac {a}{e}}.}

Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен

p=b2a.{\displaystyle p={\frac {b^{2}}{a}}.}

Фокальные радиусы, т. е. расстояния от фокусов до произвольной точки кривой (x,y){\displaystyle \left(x,\,y\right):}

r1=a+ex,r2=a−ex.{\displaystyle r_{1}=a+ex,\;\;\;r_{2}=a-ex.}

Уравнение диаметра, сопряжённого хордам с угловым коэффициентом k{\displaystyle k:}

y=−b2a2kx.{\displaystyle y=-{\frac {b^{2}}{a^{2}k}}x.}

Уравнение касательных, проходящих через точку (x1,y1){\displaystyle \left(x_{1},y_{1}\right):}

y−y1x−x1=−x1y1±b2x12+a2y12−a2b2a2−x12{\displaystyle {\frac {y-y_{1}}{x-x_{1}}}={\frac {-x_{1}y_{1}\pm {\sqrt {b^{2}x_{1}^{2}+a^{2}y_{1}^{2}-a^{2}b^{2}}}}{a^{2}-x_{1}^{2}}}}

Уравнение касательных, имеющих данный угловой коэффициент k{\displaystyle k:}:

y=kx±k2a2+b2.{\displaystyle y=kx\pm {\sqrt {k^{2}a^{2}+b^{2}}}.}

Уравнение нормали в точке (x1,y1){\displaystyle \left(x_{1},y_{1}\right):}

y−y1x−x1=a2y1b2x1.{\displaystyle {\frac {y-y_{1}}{x-x_{1}}}={\frac {a^{2}y_{1}}{b^{2}x_{1}}}.}

Параметрическое уравнение

Каноническое уравнение эллипса может быть параметризовано:

{x=acos⁡ty=bsin⁡t⩽t⩽2π,{\displaystyle {\begin{cases}x=a\,\cos t\\y=b\,\sin t\end{cases}}\;\;\;0\leqslant t\leqslant 2\pi ,}

где t{\displaystyle t\,} — параметр уравнения.

Уравнение в полярных координатах

Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах (ρ,ϕ){\displaystyle \left(\rho ,\phi \right)} будет иметь вид

ρ=p1±ecos⁡ϕ,{\displaystyle \rho ={\frac {p}{1\pm e\cos \phi }},}

где e{\displaystyle e} — эксцентриситет, а p{\displaystyle p} — фокальный параметр.
При положительном знаке перед e{\displaystyle e} второй фокус эллипса будет находиться в точке (π,−2c),{\displaystyle \left(\pi ,-2c\right),} а при отрицательном — в точке (π,2c).{\displaystyle \left(\pi ,2c\right).}.

Вывод  

Пусть r₁ и r₂ расстояния до данной точки эллипса из первого и второго фокусов.
Пусть, также полюс системы координат находится в первом фокусе, а угол ϕ{\displaystyle \phi } отсчитывается от направления на второй полюс.
Тогда, из определения эллипса,

r1+r2=2a{\displaystyle r_{1}+r_{2}=2a}.

Отсюда,

r22=(2a−r1)2=4a2−4ar1+r12{\displaystyle r_{2}^{2}=\left(2a-r_{1}\right)^{2}=4a^{2}-4ar_{1}+r_{1}^{2}}.

С другой стороны, из теоремы косинусов

r22=r12+4c2−4r1ccos⁡ϕ{\displaystyle r_{2}^{2}=r_{1}^{2}+4c^{2}-4r_{1}c\cos \phi }.

Исключая r2{\displaystyle r_{2}} из последних двух уравнений, получаем

r1=a2−c2a−ccos⁡ϕ{\displaystyle r_{1}={\frac {a^{2}-c^{2}}{a-c\cos \phi }}}

Учитывая, что

p=a(1−e2){\displaystyle p=a(1-e^{2})},

получаем искомое уравнение.

Другое уравнение в полярных координатах:

ρ2=b21−e2cos2⁡ϕ.{\displaystyle \rho ^{2}={\frac {b^{2}}{1-e^{2}\cos ^{2}\phi }}.}

Эллипс и его каноническое уравнение

Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».

Каноническое уравнение эллипса имеет вид , где – положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:

Как построить эллипс?

Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:

Пример 1

Построить эллипс, заданный уравнением

Решение
: сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения заключается в том, что оно позволяет моментально определить вершины эллипса
, которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае :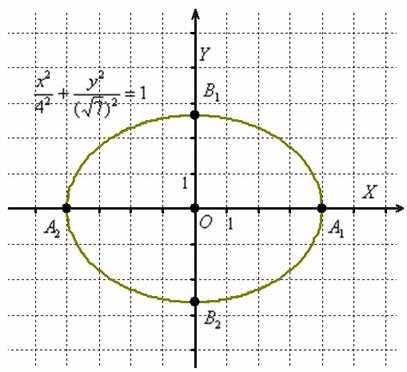Отрезок
называют большой осью
эллипса;отрезок
– малой осью
;число
называют большой полуосью
эллипса; число
– малой полуосью
.
в нашем примере: .

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы . И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса на черновике быстренько выражаем:

Далее уравнение распадается на две функции: – определяет верхнюю дугу эллипса; – определяет нижнюю дугу эллипса.

Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат
. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами . Настукаем три смс-ки на калькуляторе:
Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию: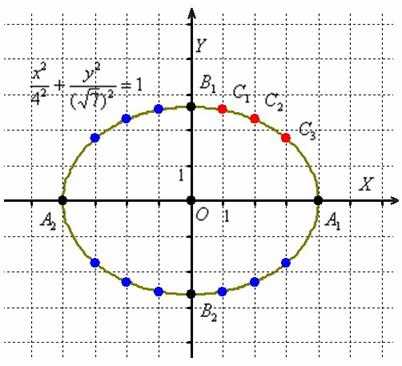
Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Уравнение эллипса

Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

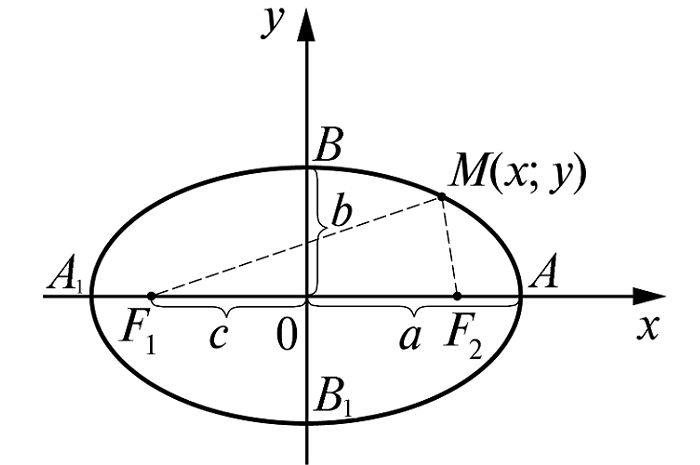
Для составления уравнения достаточно воспользоваться определением, введя обозначение:

а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F₁(-c;0); F₂(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,

a 2 b 2 = a 2 y 2 + x 2 b 2 ,

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Как построить эллипс

Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.

Построение эллипса по его большой и малой осям

Считается самым простым, не требующим серьёзных навыков.

Проведите две перпендикулярные оси;

От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;

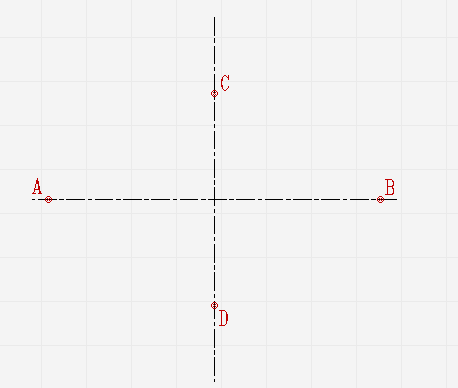
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;

Проведите ещё диаметры в различных направлениях;

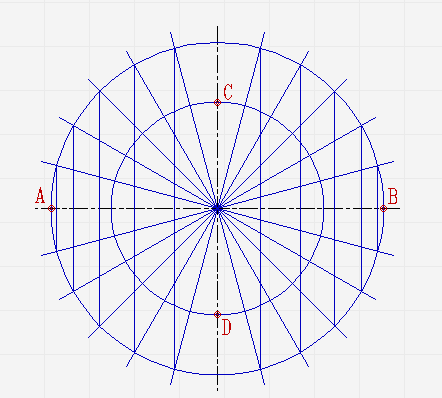
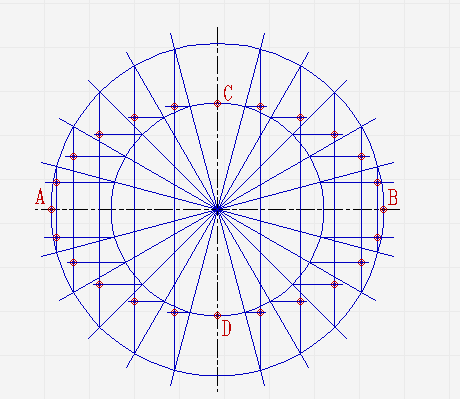
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;

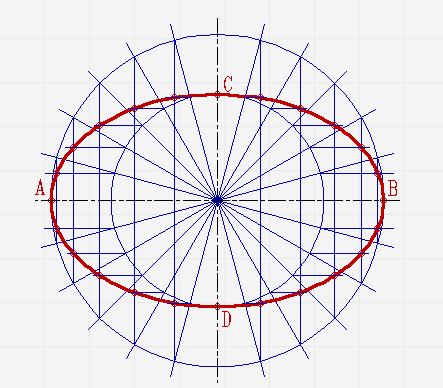
Соедините полученные точки плавной линией.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Как построить эллипс с помощью циркуля

Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.

Порядок действий следующий:

• Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
• Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
• Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P₁ и P₂. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q₁ и Q₂. Отрезки P₁P₂ и Q₁Q₂ будут большой и малой полуосями будущего эллипса;
• Установите раствор циркуля на величину a. Поместите циркуль в точке Q₁ или Q₂. После этого обозначьте циркулем на отрезке P₁P₂ точки F_{1 и} F₂. Это будут фокусы фигуры.
• Отметьте на P₁P₂ любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P₁. Затем начертите окружность данного радиуса из фокуса F₁. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P₂, но уже с центром из F₂;
• Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P₁P₂;
• Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.

Ритм

Ритм в композиции создаёт упорядоченное движение. Ритмические узоры строятся из похожих элементов и интервалов между ними.

Существует три основных типа ритма:

Регулярный ритм: интервалы между элементами предсказуемы или сами элементы схожи по размеру и длине. Регулярный ритм статичен, но делает дизайн живым за счёт контраста.

Логотип IBM построен на регулярном ритме чередующихся полосИзображение: Wikimedia Commons

Плавный ритм: повторяющиеся элементы следуют изгибам и волнистым линиям. Каждый из них при этом уникален, хоть и похож на предыдущий. В природе подобный ритм встречается в окрасе животных — тигров или зебр, он образуется на годовых кольцах деревьев или отпечатке пальца. Такое ритмическое построение создаёт ощущение плавного движения, встречаемого в природе.

В логотипе Zebra Technologies до редизайна использовали плавный, природный ритмИзображение: Zebra Technologies

Прогрессирующий ритм возникает, когда формы или фигуры при каждом своём повторении последовательно меняют форму, размер, также он может быть задан изменяющимися интервалами между элементами. Это создаёт иллюзию движения.

Логотип Spotify «излучает» звук за счёт прогрессирующего ритмаИзображение: Wikimedia Commons

Вариации в структуре всегда заставляют её выглядеть интереснее. Ритм предсказуем, а неожиданное отличие элемента выпадает из структуры и на мгновение приостанавливает движение взгляда.

Логотип Центра Помпиду состоит из линий с равномерным ритмом, которые рассекает диагональ, символизирующая лестницу на фасаде зданияИзображение: Wikimedia Commons

Психология форм в дизайне UX — практическое применение

Формы являются важными элементами во всех направлениях проектирования. Они могут служить компонентами визуальной композиции, а также инструментом организации контента, который делит или связывает элементы дизайна в группы. Чтобы сделать хороший дизайн, эксперты должны учитывать значение форм и влияние, которое они оказывают на мнение пользователей.

Графические дизайнеры часто имеют дело с небольшими, но содержательными элементами, такими как логотип и иконками. Мощный логотип должен передать правильное сообщение, которое будет выступать в роли лица бренда. Если формы выбраны надлежащим образом для логотипа, они помогут передать правильное настроение без дополнительных слов. Например, в случае логотипа для финансовой компании один из подходов может применяться для применения форм, которые передают чувство доверия и баланса, например, квадрат или треугольник.

Различные формы часто встречаются в пользовательских интерфейсах цифровых продуктов. Они могут использоваться как кнопки или иконки, а также применяются для организации контента на макете. Например, текстовые блоки часто собираются в прямоугольной или квадратной форме, что позволяет пользователям быстро сканировать текст. Используя различные формы, дизайнеры могут создавать эффективную информационную архитектуру для продукта. Элементы макета могут быть структурированы в определенных формах, чтобы пользователи легко находили основную информацию. Например, если мы разместим контент в треугольной форме, разместив на нем жизненно важный компонент, глаза людей автоматически перейдут на пик.

Психология фигур играет большую роль в типографии. Существует огромное количество шрифтов, и все они оказывают индивидуальное влияние на визуальное восприятие. Некоторые макеты применяют круглые формы как доминирующие, и они кажутся более женственными и мягкими, в отличие от тех, у кого прямые линии и острые углы, которые более формальны и иногда агрессивны

Вот почему важно обратить внимание на то, какие формы доминируют в выбранном шрифте, чтобы избежать конфликта между контекстом и визуальным представлением

Человеческий ум полон секретов, и часто трудно предсказать возможные реакции. Однако наука о психологии помогает дизайнерам подготовиться и понять, как работает наш мозг, по крайней мере, на каком-то базовом уровне. Знание психологии дизайнеров форм позволяет создавать профессиональные логотипы наряду с пользовательскими интерфейсами для решения проблемных задач для веб-и мобильных продуктов.Источник

Построение изображений в плоском зеркале

Построение изображения в плоском зеркале основано на законах отражения света.

Алгоритм построения изображения в плоском зеркале

1. Проведите из данной точки на поверхность луч под произвольным углом. В точке падения луча на границу раздела сред проведите перпендикуляр.
2. Отметьте угол падения ​\( \alpha \)​.
3. Постройте равный ему угол отражения ​\( \beta \)​.
4. Проведите из данной точки перпендикуляр к поверхности зеркала ​\( (\alpha=0) \)​.
5. Постройте равный ему угол отражения ​\( (\beta=0) \)​ (эти лучи совпадают).
6. Проведите пунктирной линией продолжения отраженных лучей за зеркало.
7. Найдите точку пересечения продолжений отраженных лучей (эта точка является изображением данной точки в плоском зеркале).
8. Аналогично постройте изображение второй точки.
9. Соедините полученные изображения точек пунктирной линией.

Изображение предмета в плоском зеркале мнимое, прямое, по размерам равное предмету, находящееся за зеркалом на таком же расстоянии, на каком предмет находится перед зеркалом.

Важно!
Если на поверхность плоского зеркала падает сходящийся пучок лучей, то изображение получается действительным

Если поверхность двух плоских зеркал образует угол ​\( \varphi \)​, то количество изображений в такой системе зеркал можно определить по формуле:

где ​\( N \)​ – количество изображений.

Продолжаем решать задачи на эллипс вместе

Если

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где

Пример 7. Дан эллипс

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е.

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.