Фигуры вращения: цилиндр, конус, шар

Задача на определение площади конической поверхности

Решим простую задачу. Необходимо найти площадь боковой поверхности конуса, если известно, что его высота h равна диаметру основания, а генератриса составляет 15 см.

Запишем соответствующую формулу для S_b, из которой будет видно, какие величины следует рассчитать. Имеем:

S_b = pi*r*g.

Значение генератрисы g известно из условия задачи. Остается определить радиус фигуры.

Генератриса, высота и радиус связаны друг с другом следующим равенством:

g2 = h2 + r2.

Из условия следует, что 2*r = h. Подставляя значение h в выражение, получим:

g2 = (2*r)2 + r2 = 5*r2 =>

r = g/√5.

Теперь формулу для радиуса основания подставляем в выражение для S_b, получаем:

S_b = pi/√5*g2.

Мы получили конечную формулу, из которой видно, что площадь искомой поверхности зависит только от длины генератрисы. Подставляя g = 15 см, получаем ответ на задачу: S_b ≈ 315,96 см2.

Просмотры: 53

Тест с ответами: “Цилиндр”

1. Дан цилиндр, длина диаметра основания которого в два раза меньше длины образующей. Объем этого цилиндра равен 108п. Вычислите диаметр основания: а) 6 + б) 14 в) 12

2. Что представляет сечение цилиндра, проведенное плоскостью, перпендикулярно оси: а) овал б) круг + в) прямоугольник

3. Вычислите длину радиуса основания равностороннего цилиндра, площадь полной поверхности которого равна 24п: а) 48 б) 12 в) 2 +

4. Что представляет осевое сечение цилиндра: а) прямоугольник + б) треугольник в) овал

5. Объем цилиндра равен произведению площади … на высоту: а) стороны б) вершины в) основания +

6. Что представляет боковая поверхность цилиндра: а) треугольник б) прямоугольник + в) круг

7. Сечение, проходящее параллельно основаниям цилиндра, является: а) прямоугольником б) квадратом в) кругом +

8. Объем цилиндра равен 64π, а площадь боковой поверхности – 32π. Найдите площадь полной поверхности цилиндра, деленную на π: а) 64 + б) 72 в) 48

9. Цилиндр, осевым сечением которого является квадрат, называется: а) правильным круглым б) эллиптическим в) равносторонним +

10. Про прямые круговые цилиндры C1 и C2 известно, что у C1 радиус основания в два раза больше, чем у C2, но у C2 высота в три раза больше, чем у C1. Найдите отношение объёма цилиндра C2 к объёму C1: а) 1 б) 0,75 + в) 1,2

11. Если диаметр основания и образующая цилиндра равны друг другу, то осевым сечением является: а) квадрат + б) круг в) прямоугольник

12. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали: а) 24 л б) 14 л + в) 12 л

13. Геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её: а) цилиндр + б) конус в) квадрат

14. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра: а) 1,20 б) 1,5 в) 1,25 +

15. Сечение, проходящее параллельно оси цилиндра, может быть: а) либо прямоугольником, либо квадратом + б) только квадратом в) только прямоугольником

16. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого: а) 18 см б) 3 см + в) 9 см

17. Если диаметр основания и образующая цилиндра не равны друг другу, то осевым сечением является: а) квадрат б) круг в) прямоугольник +

18. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали: а) 1100 см3 б) 1000 см3 + в) 100 см3

19. Вычислите длину высоты равностороннего цилиндра, площадь осевого сечения которого равна 25: а) 50 б) 12,5 в) 5 +

20. Пусть V, r, h соответственно объем, радиус и высота цилиндра. Найдите объем, если r=2√2 cм, h=3 см: а) 43π см3 б) 24π см3 + в) 31π см3

21. Сколько образующих можно провести в цилиндре: а) много + б) одну в) две

22. Радиус основания цилиндра равен 7, а высота – 10. Найдите площадь боковой поверхности цилиндра, деленную на π: а) 124 б) 140 + в) 104

23. Какой вид не может иметь сечение цилиндра: а) овал б) квадрат в) треугольник +

24. Шар вписан в цилиндр. Площадь поверхности шара равна 41. Найдите площадь полной поверхности цилиндра: а) 60 б) 61,5 + в) 55

25. Вращением какой геометрической фигуры можно получить цилиндр: а) прямоугольного треугольника вокруг гипотенузы б) прямоугольного треугольника вокруг катета в) прямоугольника вокруг одной из сторон +

26. Площадь боковой поверхности цилиндра равна 18π, а диаметр основания равен 9. Найдите высоту цилиндра: а) 4 б) 2 + в) 36

27. Площадь полной поверхности цилиндра: а) S=2п(r+h) + б) S= r(r+h) в) S=пr(r+h)

28. Поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей): а) поверхность основания цилиндра б) коническая поверхность в) цилиндрическая поверхность +

29. Площадь боковой поверхности цилиндра: а) S=пrh + б) S=2r в) S=r2

30. Отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка: а) сторона цилиндра б) высота цилиндра + в) вершина цилиндра

Элементы конуса

Определение. Вершина конуса – это точка (K), из которой исходят лучи.Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):

L2 = R2 + H2

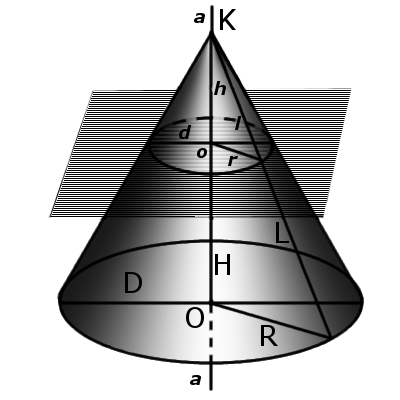
Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:

где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:

где R – радиус основы, а H – высота конуса.

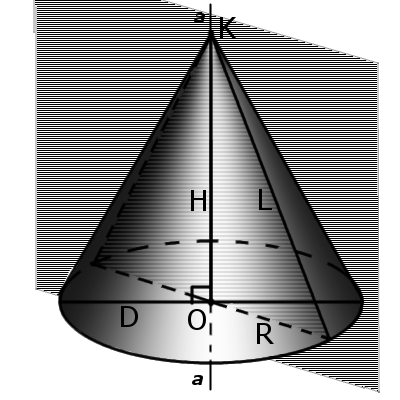
Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.

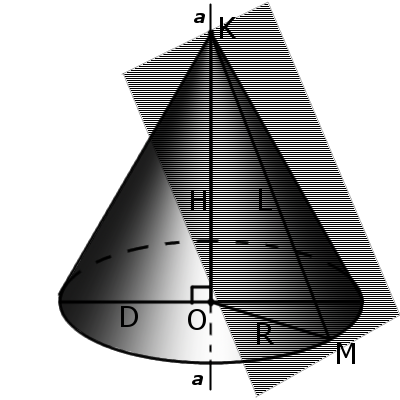
Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.

Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).

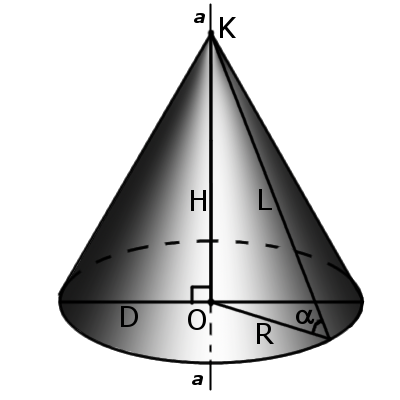
Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.

Формула. Объём кругового конуса:

где R – радиус основы, а H – высота конуса.

Формула. Площадь боковой поверхности (S_b) прямого конуса через радиус R и длину образующей L:

S_b = πRL

Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:

Sp = π RL + π R2

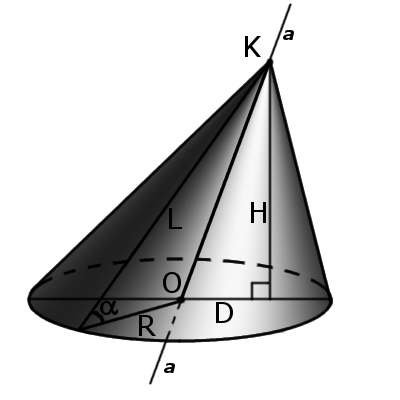
Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.

Формула. Объём любого конуса: V = 1 SH 3

где S – площадь основы, а H – высота конуса.

Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.

Формула. Объём усеченного конуса: V = 1 (S2H – S1h ) 3

где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.

Усеченный конус и его осевое сечение

Усеченный конус получается из правильного конуса с помощью секущей плоскости, параллельной основанию. Получившаяся фигура под плоскостью будет усеченным конусом. Это показано на картинке.

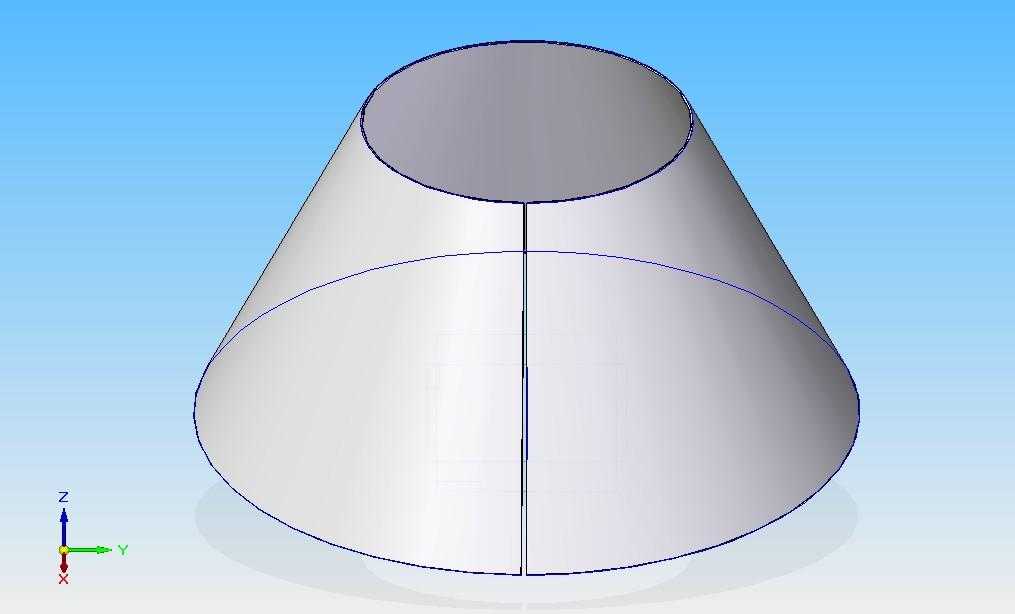
Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r1 и r2. Расстояние между основаниями называется высотой и обозначается буквой h.

Осевое сечение рассматриваемого конуса будет квадратом, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r1 и 2*r2 соответственно. Этот квадрат будет равнобедренной трапецией, как показано на рисунке ниже.

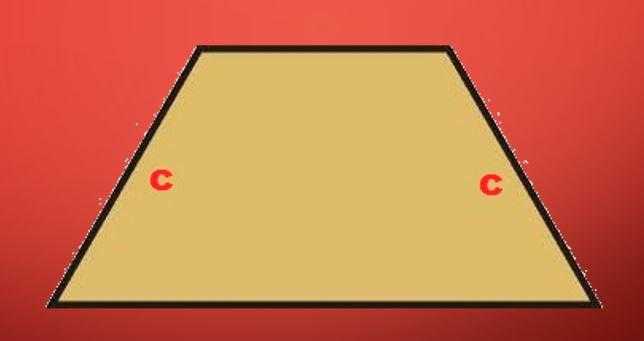
Этот факт позволяет использовать выражение для трапеции для записи формулы площади поперечного сечения усеченного осевого конуса. Он будет иметь вид:

S = (2*r1 + 2*r2)/2*h = h*(r1 + r2)

То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.

Для решения геометрических задач также может понадобиться формула связи между образующей фигуры и ее параметрами r1, r2 и h. Соответствующее выражение будет иметь вид:

g2 = h2+ (r1 — r2)2

Его довольно легко получить самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r1 — r2).

Примеры задач

Задание 1 Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.

Решение: Используем соответствующую формулу с известными нам величинами: S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см2.

Задание 2 Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.

Решение: Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):l2 = (4 см)2 + (3 см)2 = 25 см2.l = 5 см.

Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь: S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см2.

Круглый конус

Площадь боковой поверхности конуса будем рассматривать на примере круглой прямой фигуры. Такой конус представляет собой круглое основание, на которое опирается коническая поверхность. Эта фигура показана ниже.

Все генератрисы этой фигуры равны между собой. Их длина всегда больше радиуса основания. Расстояние от вершины конуса до его круглого основания называется высотой. Высота пересекает круг в его центре, поэтому конус называется прямым.

Получить этот конус не представляет никакой сложности. Для этого следует взять любой треугольник, имеющий прямой угол, и вращать его вокруг одного из катетов так, как показано ниже на схеме.

Если обозначить гипотенузу этого треугольника буквой g, а его катеты h и r, тогда будет справедливо равенство:

g2 = h2 + r2.

Для полученного конуса g — это генератриса, h — высота, r — радиус круга.

Свойства

Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2

Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cos⁡β=r/l α=180°-2β

Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)

Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h

Урок геометрии на тему «Цилиндр». 11-й класс

Оборудование и материалы:

Учитель: Тема нашего урока “Цилиндр”. С данным геометрическим телом вы знакомы давно. Какие предметы из окружающей среды напоминают вам цилиндр?

Учитель: На партах у вас развертки цилиндров. Сейчас каждый из вас заготовит цилиндр.

Прямым круговым цилиндром называют цилиндр, у которого в основании лежат круги, а образующая перпендикулярна основаниям. В дальнейшем прямой круговой цилиндр будем называть просто “цилиндр”. Его элементы: ось, радиус, высота, образующая, основания, боковая поверхность.

Нанесите на заготовленный цилиндр данные элементы и подумайте над определениями этих понятий.

Проверим, насколько верно вы дали определения.

Цилиндрическим телом или цилиндром называется тело, ограничение замкнутой цилиндрической поверхностью и двумя пересекающими её параллельными плоскостями:

— часть цилиндрической поверхности, ограничивающей цилиндр — боковая поверхность;

— части секущих параллельных плоскостей, выделяемые цилиндрической поверхностью — его основания;

— часть образующей цилиндрической поверхности — образующая цилиндра

— если в основании цилиндра круг — цилиндр круговой.

Цилиндр можно рассматривать как тело, полученное вращением прямоугольника вокруг одной из его сторон.

Рассмотрите и подумайте, как можно провести сечения, и какие геометрические фигуры получатся в результате. (Прямоугольник, овал или эллипс, круг.)

Посмотрим, как они выглядят и воспроизведем на заготовках.

Учитель: Необходимо найти площади боковой и полной поверхностей цилиндра. Как они вычисляются.

Учитель: Переходим к проверке практической работы.

Проверочная работа

Тесты по геометрии на тему “Цилиндр”

Взаимопроверка теста

Ответы теста :1в- 2, 2в-3, 3в-3, 4в-2, 5в-3, 6в-4, 7в-1, 8в-2, 9в-3, 10в-4

Учитель подводит итоги урока, анализирует уровень усвоения теоретического материала, задает задание на дом.

Примеры задач

Решение: Используем соответствующую формулу с известными нам величинами: S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см 2 .

Задание 2 Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.

Боковая поверхность усеченной фигуры

Выше было сказано, что представляет собой боковая поверхность для конуса усеченного. Разрезая ее вдоль одной из генератрис, получим следующий результат.

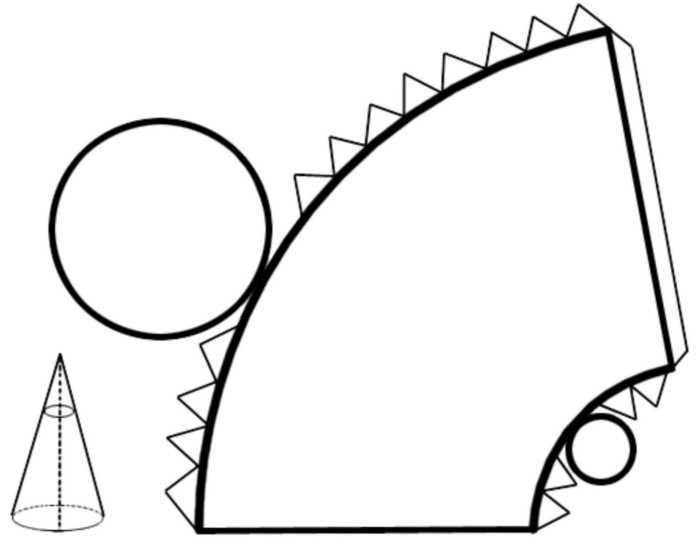
Два круга представляют собой основания. Четырехугольная фигура, ограниченная двумя прямыми отрезками и двумя дугами — это искомая боковая поверхность усеченного конуса, площадь которой необходимо найти. Решим эту задачу.

Заметим, что эта поверхность представляет собой сектор круга, у которого вырезана центральная часть. Обозначим радиус внешней дуги как g. Тогда радиус внутренней дуги будет равен g — l. Используя результаты решения предыдущей пропорции при определении угла сектора x, можно записать следующее равенство:

x = 2*pi*r₁/g = 2*pi*r₂/(g-l) =>

g = l*r₁/(r₁-r₂).

Искомая площадь S_b равна разнице площадей секторов, построенных с помощью радиусов g и g-l. Используя формулу для площади сектора, полученную выше, можно записать:

S_b = pi*g*r₁ — pi*(g-l)*r₂.

Подставляя в это выражение формулу для g, получаем конечное равенство для площади боковой поверхности конуса усеченного:

S_b = pi*l*(r₁+r₂).

Формула вычисления площади конуса

1. Боковая поверхность

Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.

S_бок. = πRl

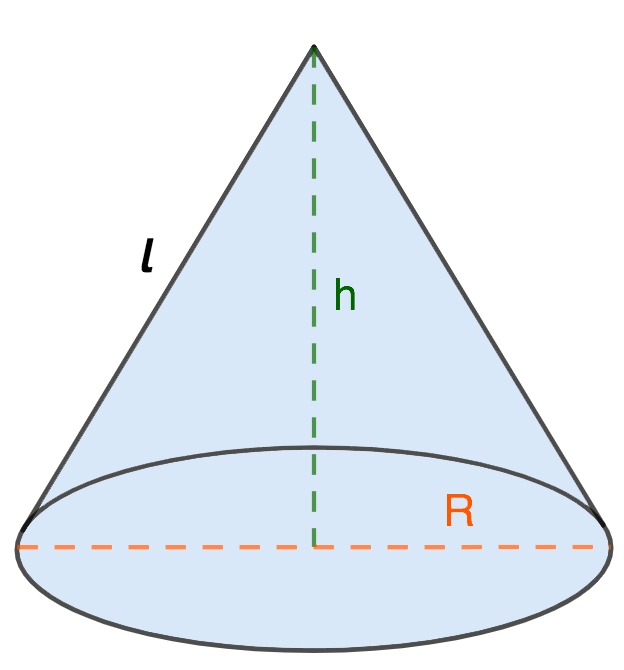
Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

Основанием конуса является круг, площадь которого вычисляется так:

S_осн. = πR2

Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:

S_осн. = π(d/2)2

3. Полная площадь

Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:

S_полн. = πRl + πR2 = πR(l + R)

рассчитать площадь поверхностирассчитать площадь поверхностиПолная площадь черезПолная площадь черезПолная площадь черезФормула площади полнойПолная площадь черезполной площади поверхности Площадь конуса Площадь усеченногоплощадь поверхности конусаплощадь поверхности конусаБоковая поверхность черезБоковая поверхность черезБоковая поверхность черезбоковой поверхности конуса

окружностикалькуляторобъемапирамидыпериметраправильнойматематикарисцилиндраpiонлайнгеометриятрапециинахождениемстатьясектородногосвойствакубапустьугловназываютвписаннойточкусайташараконическуювокругработыalphaпароль

Аналитическое описание

Вертикальный круговой конус (двойной конус) с острием в начале координат и осью z в качестве оси симметрии можно выразить уравнением

Икс2+у2знак равноР.2z2{\ displaystyle x ^ {2} + y ^ {2} = R ^ {2} z ^ {2}}

описывать. Число — это радиус высот кружков высот . Is уравнение упрощается до
Р.{\ displaystyle R}zзнак равно±1{\ displaystyle z = \ pm 1}Р.знак равно1{\ Displaystyle R = 1}

Икс2+у2знак равноz2{\ displaystyle x ^ {2} + y ^ {2} = z ^ {2}}

и в этом случае конус называется единичным конусом (аналог единичной окружности).

Подобно тому, как любой эллипс является , любой конус (как квадрика ) является аффинным образом единичного конуса . Простейшие аффинные отображения — это масштабирование координат. Масштабирование осей x и y приводит к конусам с уравнениями

Kаб:Икс2а2+у2б2знак равноz2;а,б>0.{\ displaystyle K_ {ab} \ двоеточие \, {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = z ^ {2}; \; \; a, b> 0.}

Векторы для параметрического представления эллиптического конуса

Вертикальные сечения таких конусов представляют собой эллипсы. Пересечение с плоскостью возвышения — это эллипс . Конус равен объединению всех прямых (образующих), проходящих через вершину и точки эллипса. Если эллипс описывается параметрическим представлением, а генераторы представлены в параметрической форме, получается следующее параметрическое представление конуса :
zзнак равно1{\ displaystyle z = 1}Э.Икс2а2+у2б2знак равно1{\ displaystyle E \ двоеточие {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1}Э.{\ displaystyle E}Икс→(т)знак равно(апотому что⁡т,бгрех⁡т,1){\ Displaystyle {\ vec {x}} (т) = (а \ соз т, б \ грех т, 1)}Kаб{\ displaystyle K_ {from}}

Kаб:Икс→(s,т)знак равноs⋅(апотому что⁡т,бгрех⁡т,1)Т;s∈Р.,0≤т

Уравнение конуса, расположенного где-либо в пространстве, дать сложно. С другой стороны, параметрическое представление любого конуса относительно просто:

Икс→(s,т)знак равноq→0+sж→1потому что⁡т+sж→2грех⁡т+sж→3; s∈Р.,0≤ т

Вот вершина конуса и три линейно независимых вектора. указывает в направлении оси конуса (см. рисунок). Для каждого постоянного параметра есть эллипс, с помощью которого можно представить (вместе с острием) генерируемый конус.
q→{\ displaystyle {\ vec {q}} _ {0}}ж→1,ж→2,ж→3{\ displaystyle {\ vec {f}} _ {1}, {\ vec {f}} _ {2}, {\ vec {f}} _ {3}}ж→3{\ displaystyle {\ vec {f}} _ {3}}s{\ displaystyle s}

Если три вектора попарно ортогональны и равны , то параметрическое представление описывает перпендикулярный круговой конус.
ж→1,ж→2,ж→3{\ displaystyle {\ vec {f}} _ {1}, {\ vec {f}} _ {2}, {\ vec {f}} _ {3}}|ж→1|знак равно|ж→2|{\ displaystyle | {\ vec {f}} _ {1} | = | {\ vec {f}} _ {2} |}

Тот факт, что любой эллиптический конус всегда содержит круги, показан в плоскости кругового сечения.

Площадь боковой поверхности конуса через его радиус и высоту

Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.
Так как конус прямой, то треугольник AOS – прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем:
Отсюда:
Но
Тогда:
Подставим данное выражение в формулу площади боковой поверхности конуса:
Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса

Пример расчета площади боковой поверхности конуса, если известны его радиус и высота.
Найти площадь боковой поверхности конуса с радиусом равным 1 см и высотой, равной 5 см
По условию задачи Н = 5см, R=1см
Формула боковой поверхности конуса:
Подставив в формулу значения из условия задачи, имеем:

Элементы конуса

Определение.Вершина конусаОпределение.Основание конусаОпределение.Образующей конусаФормула.Длина образующей

L2 = R2 + H2

Определение.НаправляющаяОпределение.Боковая поверхностьОпределение.ПоверхностьОпределение.ВысотаОпределение.ОсьaОпределение.Конусность (С)d

C =	D	и C =	D – d
H	h

α = 2arctg	R
H

где R – радиус основы, а H – высота конуса.

Определение.круговым, эллиптическим, гиперболическимпараболическим

Формула.Объём кругового конуса

V =	1	πHR2
3

где R – радиус основы, а H – высота конуса.

Формула.Площадь боковой поверхности_b

S_b = πRL

Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:

Sp = π RL + π R2

Формула. Объём любого конуса: V = 1 SH 3

где S – площадь основы, а H – высота конуса.

Формула. Объём усеченного конуса: V = 1 (S2H – S1h ) 3

Выкройка овального и наклонного конуса

Главная > Геометрия > Выкройка овального и наклонного конуса

24.09.2014 // Владимир Трунов

В статье Выкройка для конуса мы рассмотрели построение выкройки для круглого прямого конуса, то есть конуса, имеющего в основании круг, и ось которого перпендикулярна основанию. Там мы обошлись несколькими простыми формулами.

Теперь речь пойдет о том, как построить выкройку (развертку) для овального и наклонного конуса. Под овальным конусом будем подразумевать конус, в основании которого лежит эллипс (как наиболее гармоничный из овалов). Наклонным конусом назовем конус, проекция вершины которого (или мнимой вершины, если конус усеченный) на плоскость основания не совпадает с центром эллипса. И тут я должен сообщить две новости, как водится, хорошую и плохую. Начну с плохой. Не существует простых формул для построения таких выкроек. Есть только жуткие интегралы. Но в них мы закапываться не будем благодаря хорошей новости: у нас есть компьютер. И есть такое понятие как численные методы. Коротко говоря, это выполнение огромного количества простейших операций над числами, в результате которых появляется возможность решить задачу, нерешаемую аналитически (то есть при помощи формул). И надо только найти человека, который изобрел бы алгоритм для решения нашей задачи, и хорошо ему заплатить.

К счастью, такой человек нашелся, придумал алгоритм, запрограммировал его и публикует сегодня в виде новой версии программы Cones. Зовут его Владимир Трунов, и все благодарности — к нему.

Нет никакого смысла вникать в подробности численного метода, реализованного в программе Cones для построения выкроек овальных и наклонных конусов. Скажу только, что основой его является разбиение эллипса на множество мелких отрезков и вычисление для каждой вершины полученного многоугольника значений длины образующей конуса и приращения угла развертки. Благодаря этому в вычислениях используются только тригонометрические функции и теорема Пифагора.

Понятно, что полученные значения, а стало быть и рисунок, построенный по ним, имеют некоторую погрешность. Эта погрешность тем меньше, чем ближе конус к круглому и прямому. Если отношение большего диаметра эллипса к меньшему не превышает 2, а угол наклона оси (от вертикали) — не более 30 градусов, то погрешность в линейных размерах боковой поверхности выкройки не выйдет за 1%. (В более экзотических случаях погрешность может быть и больше, но в следующих версиях программы алгоритм будет совершенствоваться с целью ее минимизации.)

Фигуры вращения: цилиндр, конус, шар — с примерами решения

Задача на определение площади конической поверхности

Тест с ответами: “Цилиндр”

Элементы конуса

Усеченный конус и его осевое сечение

Примеры задач

Круглый конус

Свойства

Урок геометрии на тему «Цилиндр». 11-й класс

Примеры задач

Боковая поверхность усеченной фигуры