Луч

Обозначения луча

Существует несколько способов обозначения луча:

1. Самый простой — латинская буква. Принято использовать маленькие (маленькие) буквы;
2. Используются две заглавные (заглавные) буквы. При этом один из них обязательно должен указывать на начало луча. А второе — это абсолютно любая точка, расположенная на луче.

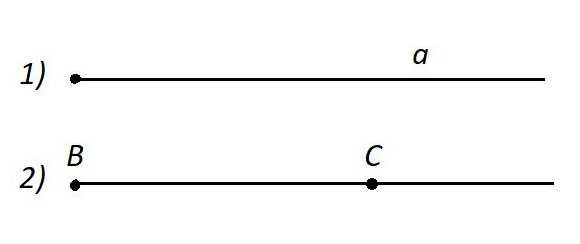
На следующем изображении хорошо видны эти обозначения. Первый вариант — это просто буква «а», она может быть где угодно. А другой — ВС, где В — начало луча.

А бывает, что на луче располагается не одна точка, а две и даже больше. Например, как на следующем рисунке.

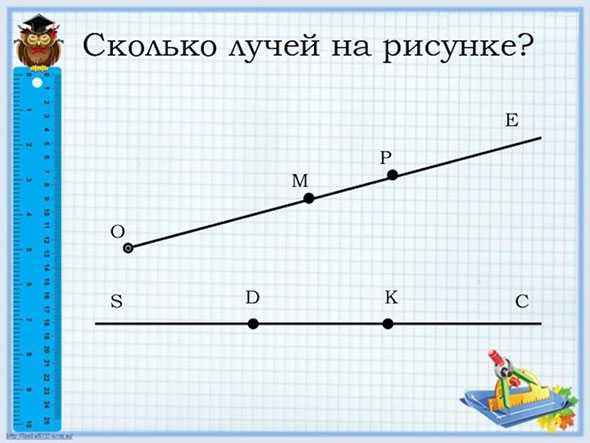
Попробуем ответить на этот вопрос. Так на верхней линии сразу 6 лучей — ОЕ, ОМ, ОП, МЕ, МП и ПЕ. Все размещаются слева направо. Но нельзя считать лучи в обратном направлении, так как прямая заканчивается в определенной точке О, а луч бесконечен.

В нижней строке тоже 6 лучей — ДК, ДК, КС, КД, КС и ДС. Здесь можно считать в обе стороны, так как линия не заканчивается. Также лучи ДК и КД хоть и выглядят одинаково из-за буквенного обозначения, но являются совершенно разными частями линии. У них разный центр (D и K соответственно) и они тоже направлены в противоположные стороны. И это те самые дополнительные лучи, о которых мы говорили выше.

Определение понятий

Открытый луч

Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .

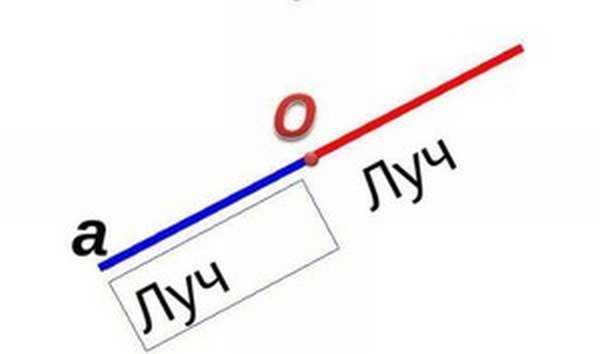В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.

Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.

Обозначения в геометрии

Вариантов для обозначения несколько:

1. Попробуйте провести на тетрадном листе линию. Представим, что у вас имеется полупрямая «О». Точка О — исходная, другой быть не может. Это самый распространенный способ.
2. Данный метод более интересен: нашу полупрямую возможно назвать не одной буквой. К примеру, на одной линии может быть их две, где первая — начало (буква О), а вторая расположена на каком-то расстоянии. Представим, что на отрезке длиной 10 сантиметров начало названо буквой О, а на расстоянии четырех сантиметров от (О) находится вторая точка (В). Тогда его обозначают «ОВ».
3. Третий способ — это когда О у нас располагается не в начале, а с каким-то отступом. Итак, снова начертите прямую с длиной десять сантиметров, отступите слева один сантиметр и отметьте начало. Снова назовите буквой О. В центре точку не ставьте, но обозначьте данную область буквой К. В этот раз буква О — это его начало. Название читается как «ОК»:
   • Для начала начертим дополняющие лучи. Как мы уже разобрались, на прямой нужно поставить точку (называем ее О), она производная и разделяет ее на 2 линии, которые пересечься не могут.
   • Перейдем к следующему этапу. Теперь нам нужно начертить продолжение — линию, имеющую общее начало с основополагающей, но не совпадающей с нею. А именно: дополняющая линия не является продолжением.
   • Чтоб начертить продолжение, проведем из О прямую, которая не располагается на дополняющих, но имеет с ними одно начало. После того как начертили, отметим на новом луче точку В. ОВ теперь лежит на его продолжении из О.

Величина угла

Помимо сравнения одних углов с другими также часто необходимо измерение углов. Измерить угол означает найти его величину. Для этого необходимо выбрать какой-то «эталонный» угол, который мы будем принимать за единицу. Чаще всего таким углом является угол, который равен $\frac{1}{180}$ части развернутого угла. Такую величину называют градусом. После выбора такого угла мы проводим с ним сравнение углов, величину которого нужно найти.

Самым простым способом измерения величины углов является измерение с помощью транспортира.

Пример 1

Найти величину следующего угла:

Решение.

Используем транспортир:

Получим

Ответ: $30^0$.

После определения величины углов у нас появляется второй способ для сравнения углов. Если при одном и том же выборе единицы измерения угол 1 и угол 2 будут иметь одинаковую величину, то такие углы будут называться равными. Если же, без ограничения общности, угол 1 будет иметь величину по числовому значению меньше величины угла 2, то угол 1 будет меньше угла 2.

Применение полупрямых и лучей в геометрии и физике

Полупрямая и луч — это важные понятия в геометрии и физике, которые находят широкое применение в различных областях знания. Вот несколько примеров использования полупрямых и лучей:

1. Геометрия:

   • Полупрямая и луч используются для изучения свойств геометрических фигур, таких как треугольники, прямоугольники, окружности и другие.
   • Они помогают определить геометрические преобразования, такие как отражение, поворот и сдвиг.
   • Полупрямые и лучи используются для построения углов и измерения их величины.
   • Они также применяются в анализе и решении геометрических задач.

2. Физика:

   • Полупрямая и луч используются для изучения и описания световых и электромагнитных явлений.
   • Они помогают определить направление распространения света и его взаимодействие с поверхностями.
   • Полупрямые и лучи используются для построения оптических систем, таких как линзы и зеркала.
   • Они также применяются в анализе и решении задач, связанных с распространением звука и других типов волн.

В обоих случаях полупрямая и луч являются важными инструментами для изучения и понимания различных явлений и объектов. Их использование позволяет упростить анализ и решение задач, связанных с геометрией и физикой, и дает возможность получить более точные результаты.

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

Линия может быть

1. замкнутой, если её начало и конец находятся в одной точке,
2. разомкнутой, если её начало и конец не соединены

Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.


Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.


Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

1. самопересекающейся
2. без самопересечений

1. прямой
2. ломанной
3. кривой

Классификация лучей

Если взять два луча, то они могут располагаться по-разному по отношению друг к другу:

1. Параллельно. Оба луча идут параллельно и никогда не пересекаются.
2. Крейсерская. Лучи имеют одну общую точку, но она не является основанием.
3. Дополнительный. Хотя мы уже говорили о них, они должны быть в этом списке. Помните, что это лучи, которые имеют общий центр и к тому же расположены на одной прямой — просто они идут в противоположных направлениях.
4. И, наконец, есть лучи, также имеющие общий центр, но не лежащие на одной прямой. А затем они образуют еще один геометрический элемент, который называется углом.

Есть даже определение:

Луч – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки.

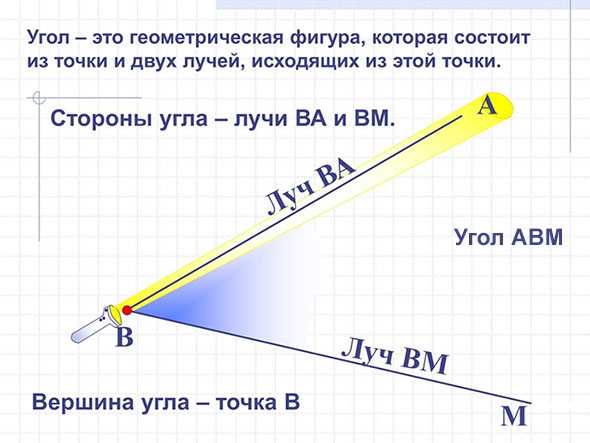
Следовательно, луч всегда обозначается тремя буквами, где отражаются оба луча. В этом случае буква, обозначающая середину, всегда находится посередине.

Вот и все, что мы хотели рассказать о таком понятии, как ЛУЧ.

Особенности отражения совпадающих лучей

Отражение совпадающих лучей — это явление, при котором приходящие на поверхность лучи света отражаются таким образом, что их направления остаются неизменными. Это происходит, когда лучи падают под прямым углом на поверхность или падают параллельно ей.

При отражении совпадающих лучей наблюдаются следующие особенности:

1. Отражение от зеркальной поверхности: Если лучи падают на плоскую, гладкую и зеркальную поверхность под прямым углом, то они отражаются таким же прямым углом в противоположном направлении. Это явление наблюдается, например, при отражении света от зеркала или глянцевой поверхности.
2. Отражение от рифленой поверхности: Если лучи падают на неровную поверхность, то они отражаются в разных направлениях. При этом каждый луч отражается под прямым углом к нормали к поверхности в точке падения. Это явление наблюдается, например, при отражении света от матовой поверхности или бумаги.

Отражение совпадающих лучей — важное явление в геометрии и оптике. Оно позволяет понять, как свет распространяется и взаимодействует с различными поверхностями

Отличие световых лучей от геометрических

В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света
. Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.

Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.

Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча
.

Если взять произвольную прямую a
, и отметим на ней некоторую точку О
, то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.

Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k
.

Также можно обозначать луч двумя большими латинским буквами. При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.

На рисунке представлен луч ОС.

Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.

Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми
.

Применение полупрямой и луча в реальной жизни

Понимание концепции полупрямой и луча может быть полезным в различных сферах реальной жизни. Ниже приведены примеры использования полупрямой и луча в разных областях.

1. Геометрия и математика

В геометрии и математике полупрямая и луч играют важную роль. Они используются для описания направления или линии движения. Например:

• В треугольниках полупрямые и лучи могут использоваться для определения углов и сторон;
• В графиках и координатных системах полупрямая может использоваться для отображения линии тренда или направления;
• При решении задач на построение графиков, полупрямые и лучи могут помочь определить направление роста или убывания значения функции.

2. Оптика и физика

В оптике и физике полупрямая и луч используются для описания пути света. Например:

• В оптических системах полупрямая или луч света может использоваться для описания его движения от источника света к наблюдателю или отражения и преломления;
• При изучении отражения и преломления света, полупрямая и луч используются для описания угла падения и угла отражения или преломления.

3. Архитектура и строительство

В архитектуре и строительстве полупрямая и луч могут использоваться для указания направления, расположения и выравнивания элементов:

• При планировании размещения окон и светопропускающих конструкций, полупрямые и лучи используются для определения направления освещения;
• При создании пространственных композиций и проектировании зданий, полупрямая и луч могут быть использованы для подчеркивания линий или акцентирования деталей;
• При построении линий перпендикулярных или параллельных стенам или другим элементам, полупрямые и лучи могут использоваться для обеспечения точности и плавности.

Это лишь несколько примеров использования полупрямой и луча в реальной жизни. Концепция полупрямой и луча может быть применена во многих других областях, где требуется определить направление, линию движения или путь распространения.

Сравнение углов

Рассмотрим два произвольных угла. Очевидно, что они могут быть либо равными, либо неравными.

Итак, для сравнения выбранных нами углов (обозначим их угол 1 и угол 2) наложим вершину угла 1 на вершину угла 2, так, чтобы, по одному из лучей этих углов наложились друг на друга, а другие два были по одну сторону от этих лучей. После такого наложения возможны два следующих случая:

1. Вторые лучи этих углов также совпадут. В таком случае мы получим, что такие углы будут равны друг другу
   (рис. 4).

2. Вторые лучи не совпадут. Здесь, без ограничения общности, будем считать, что луч угла 1 будет лежать внутри угла 2. Тогда здесь мы говорим, что данные углы не равны, причем угол 1 меньше угла 2
   (рис. 5).

Различия между полупрямой и лучом

Полупрямая и луч – это геометрические понятия, которые используются для описания линий в плоскости. Между ними есть некоторые различия.

Полупрямая:

• Полупрямая – это часть прямой, которая имеет один начальный точечный источник и простирается в бесконечность в одном направлении.
• У полупрямой есть начальная точка и она нетерминируема, то есть не имеет конечной точки.
• Полупрямая обозначается с помощью двух букв, причем начальная точка указывается первой.
• Полупрямую можно визуализировать как стрелку, начало которой соответствует начальной точке, а остальная часть простирается в бесконечность в одном направлении.
• Пример полупрямой: AB →.

Луч:

• Луч – это часть прямой, которая имеет один начальный точечный источник и простирается в определенном направлении, но не имеет конечной точки.
• У луча есть начальная точка и он также нетерминируем, то есть не имеет конечной точки.
• Луч обозначается с помощью двух букв, причем начальная точка указывается первой.
• Луч можно визуализировать как полупрямую, но без стрелки и только в одном направлении.
• Пример луча: CD -.

Таким образом, основное различие между полупрямой и лучом заключается в направлении простираемой части – полупрямая простирается в обе стороны, а луч простирается только в одном направлении.

Сравнение

Из определений видно, что кардинальное отличие луча от прямой заключается в том, ограниченны ли они в пространстве. Так, луч обязательно имеет начало и продолжается только с одной стороны. У прямой, в свою очередь, нет предела ни с того, ни с другого края. В связи с этим начертить можно лишь ее часть, что, впрочем, относится и к лучу.

Если взять на прямой произвольную точку, то отходящая от нее бесконечная линия будет являться лучом. В этом смысле луч можно назвать частью прямой. Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно направленных лучей.

Сравнивая луч и прямую, следует сказать о способах их обозначения. Каждый из геометрических объектов может называться латинской строчной буквой: луч a (с, d, t) или прямая b (a, h, c). Также в том и другом случае используется обозначение двумя заглавными буквами: луч NK или прямая OD.

Однако в последнем пункте имеются отличия. Буквы в названии прямой, помечающие точки, через которые она проведена, при чтении и записи можно менять местами. Между тем относительно луча первым указывается строго его начало, а затем точка, расположенная на определенном расстоянии от исходной.

Кроме того, луч имеет собственный вариант обозначения. В этом случае после заглавного символа, называющего начальную точку, с помощью строчной буквы указывается прямая, на которой расположен луч. Таким образом, обозначение Bo трактуется так: луч с началом в точке B принадлежит прямой o.

В чем разница между лучом и прямой, кроме сказанного? В том, что лучи могут образовывать угол. Для этого они должны исходить из одной точки. Прямые углов не образуют.

Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем , что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.

Обозначение прямой

В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита .

Иногда обозначение прямой линии происходит при помощи двух точек , которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.

Например, на рисунке 1 обозначены такие прямые:

• c
• KL

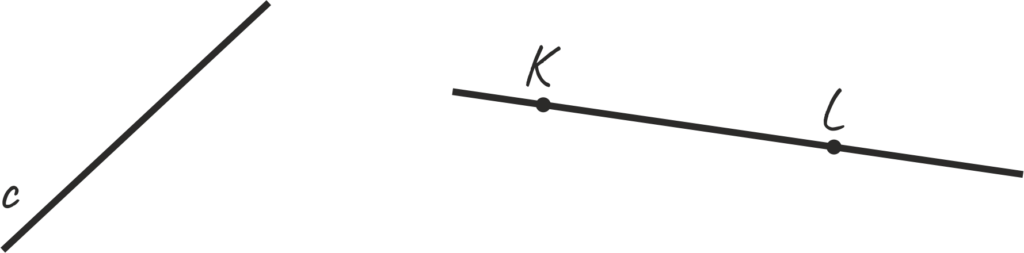
Рис. 1 Обозначение прямой линии

Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек .

Рис. 2 Обозначение прямой с несколькими точками

На рисунке 2 видно, что на одной прямой b лежат четыре точки: D , G , H , O . Поэтому данную прямую мы можем назвать любым из этих семи имен: b , DG , DH , DO , GH , GO или HO .

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются .

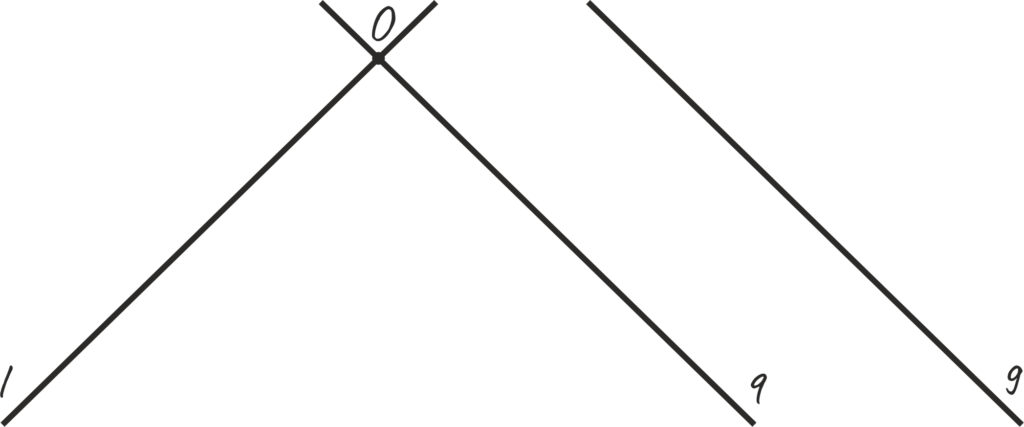
Рис. 5 Пересечение прямых

На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O , а прямые q и g не пересекаются.

Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q .

Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g , то станет понятно, что они тоже пересекаются.

Взаимное расположение точек и прямой , а также их обозначение, точно такое же, как и у всех линий вообще.

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O , которую называют началом луча.

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

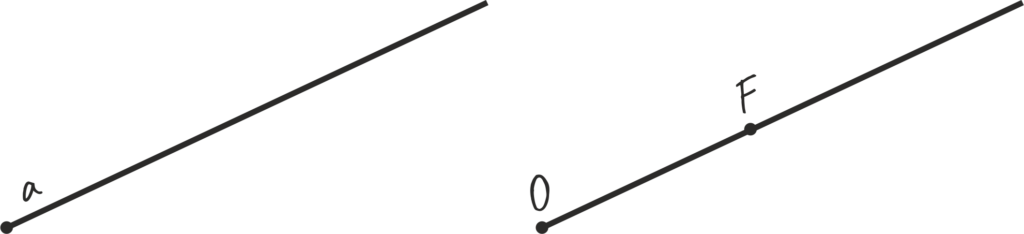
Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

• a – строчной (маленькая) буква латинского алфавита;
• OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.

Луч имеет второе название – полупрямая.

Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами , поскольку в соединенном виде они формируют одну прямую линию в точке их начала.

Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие , или говорят, что эти лучи совпадают .

Конечен ли луч света?

Свет и цвет

Если направить луч света от фонарика на какой-нибудь объект, мы увидим его след в виде круглого сечения. Но, что будет, если направить свет вдаль, например, на небо? Он при этом будет продолжаться бесконечно либо все-таки у луча есть конечная точка?

Из чего состоит световой луч?

Световой луч в оптике – это линия, вдоль которой перемещается энергия света. Проще говоря, это пучок света, имеющий небольшую толщину. В свою очередь, свет представляет собой электромагнитное излучение (либо волны), которое человек воспринимает глазами.

Глаз человека способен различать лишь определенный диапазон излучения

Помимо видимой части, электромагнитное излучение также бывает и невидимым для наших глаз. Сюда относятся микроволны, инфракрасное, ультрафиолетовое излучение, рентгеновские лучи и др.

Световой луч состоит из фотонов – элементарных мельчайших частиц. Фотоны считаются одновременно и волнами, и частицами. У них нулевая масса и электрический заряд, нет определенного размера и структуры. При этом фотоны переносят электромагнитное взаимодействие и двигаются со скоростью света.

Фотоны могут отражаться и поглощаться материей. У них имеется определенная энергия и именно от нее зависит цвет, который субъективно воспринимают наши глаза. Видимый диапазон довольно небольшой, а остальные виды электромагнитного излучения улавливаются и фиксируются специальными приборами.

Есть ли у луча света начало и конец?

Представим световой луч в виде прямой линии. У нее обязательно есть начало. Чертить линию, казалось бы, можно бесконечно. Однако если прекратить это делать, линия оборвется на конечной точке.

Так как луч света состоит из фотонов, он представляет собой нечто более сложное, чем просто линию. Поскольку у данных частиц нет массы, то и никакие силы на них не действуют. Передвигаясь со скоростью света, фотоны «живут» в своем ритме, не очень понятном для нас.

Свет прямолинеен лишь в однородной среде, а в неоднородной он образует несколько пучков

Для фотона период его жизни занимает буквально мгновение от зарождения и до того момента, как его поглотит какой либо объект. Началом луча является источник света. В вакууме (космическом пространстве) фотоны будут двигаться бесконечно. Они просто не сталкиваются с какими-либо препятствиями на своем пути.

Для фотона есть только 2 варианта развития событий, если он встречается с объектом: отражение или поглощение. Что именно произойдет, зависит от самого объекта. Например, если включить свет в комнате, она наполнится огромнейшим количеством фотонов.

Они начнут двигаться в пределах помещения, то и дело сталкиваясь с окружающими предметами. При этом одни частицы отражаются от предмета, а другие – поглощаются им и передают свою энергию. Затем предмет излучает новые фотоны, но уже с меньшей энергией.

Пока свет в комнате включен, все эти процессы протекают без остановки, ведь каждую секунду вырабатываются новые частицы. Если выключить свет, уже выработанные фотоны продолжают движение до определенного момента, пока не потеряется вся энергия. Для наших глаз свет, естественно, исчезает практически мгновенно – можно заметить, что мы еще пару секунд продолжаем видать предметы в темноте.

Чем дальше от источника свет, тем шире становится его луч

В пространстве без каких-либо ограничений световой луч будет продолжаться бесконечно. Однако чем дальше от источника, тем больше становится поперечное сечение луча. Таким образом, фотоны рассеиваются все сильнее и сильнее по определенной области, но не исчезают совсем.

Чем дальше от источника света находится наблюдатель, тем меньшее количество фотонов улавливает глаз. Поэтому световой луч становится слабее. Но фотон не может распадаться, так как это стабильная частица.

У луча света есть начало (источник), но нет конца. Он состоит из множества фотонов, которые двигаются прямолинейно. Фотон – это неделимая элементарная частица (и волна), которая не может исчезнуть просто так. Если на пути светового луча нет препятствий, то он продолжается бесконечно, хоть и рассеивается постепенно из-за увеличения поперечного сечения.

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.