Условие коллинеарности векторов

Слайд 31. Введение.Кто не знает, в какуюгавань он плывёт, для того

нет попутного ветраСенека Опираясь на слова философа Сенеки я решила

точно определить себе «гавань». Для изучения её мной была взята тема векторы. Она возникла в связи с интересом к данному изученному объекту. На уроках алгебры и геометрии мы знакомились лишь только с векторами на плоскости, но мной была взята тема векторы в пространстве. Я старалась изучить их настолько насколько позволяют мои знания. Результат должен быть следующим: узнать больше о самом историческом понятии вектор (геометрия, как всякая математическая наука, строится путём образования абстрактных понятий и логических доказательства предложений, касающихся этих понятий).

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

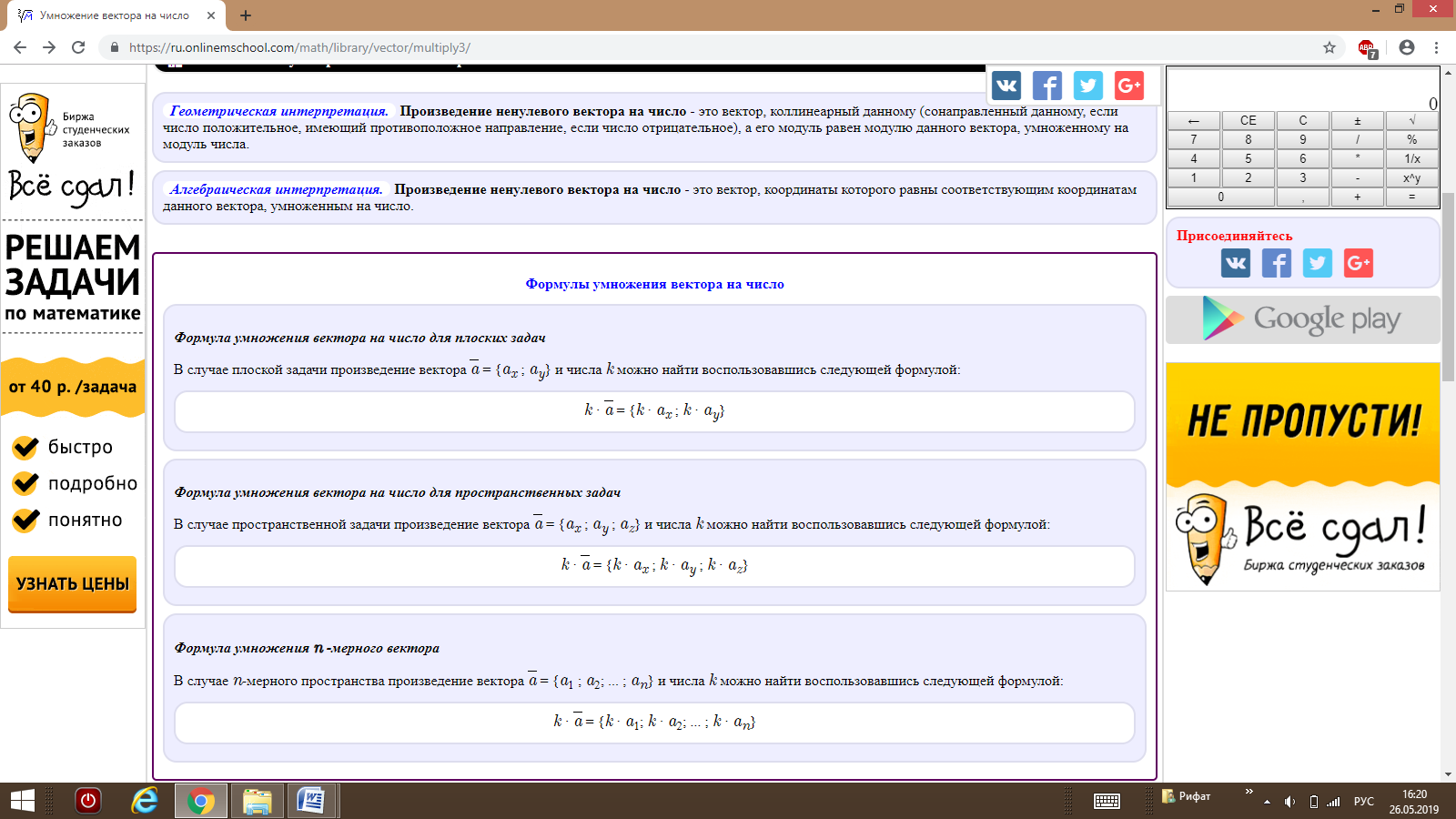
В случае плоской задачи скалярное произведение векторов a = x ; a _y > и b = x ; b _y > можно найти воспользовавшись следующей формулой:

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = x ; a _y ; a _z > и b = x ; b _y ; b _z > можно найти воспользовавшись следующей формулой:

Формула скалярного произведения n -мерных векторов

В случае n -мерного пространства скалярное произведение векторов a = 1 ; a ₂ ; . ; a _n > и b = 1 ; b ₂ ; . ; b _n > можно найти воспользовавшись следующей формулой:

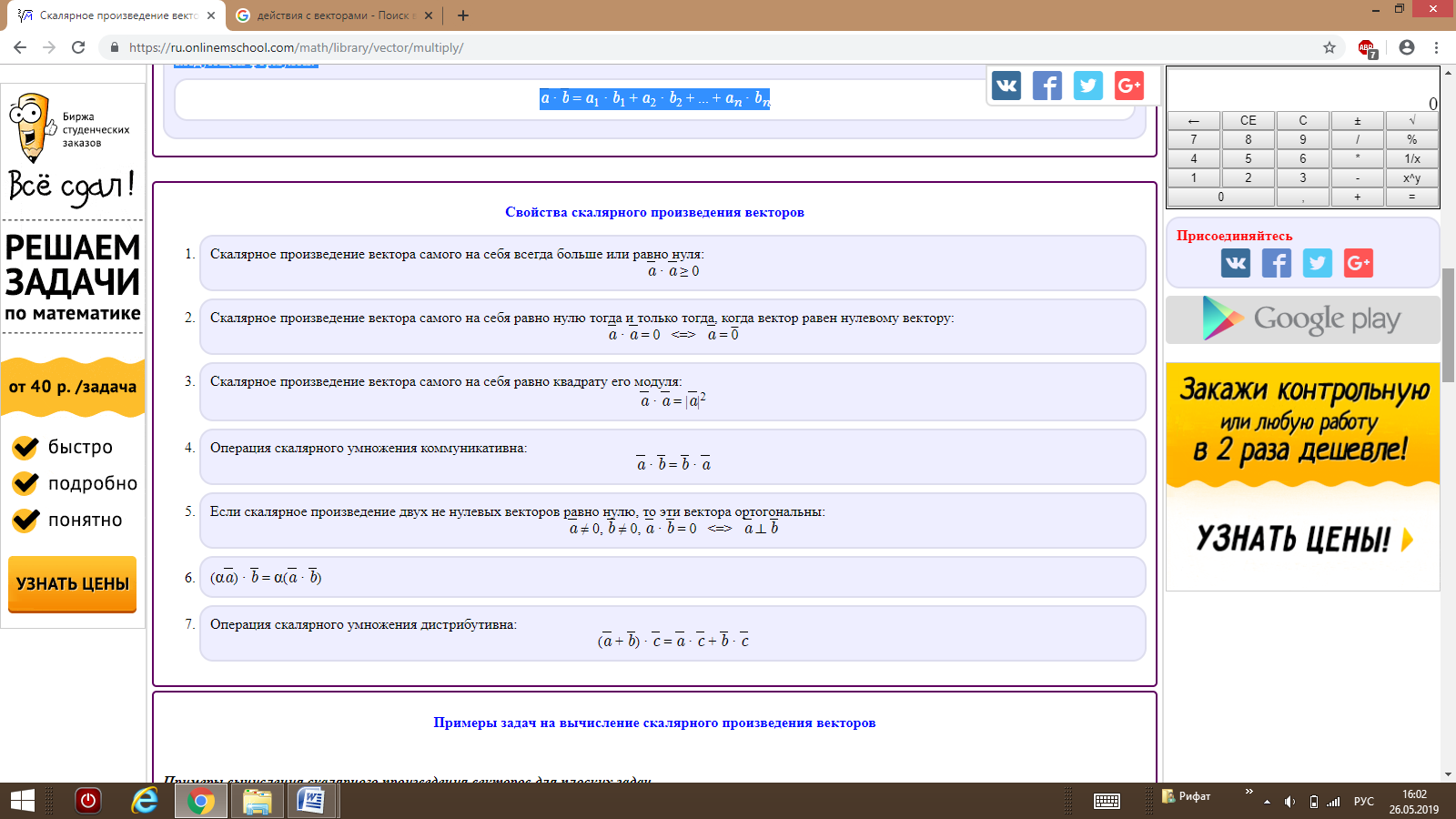
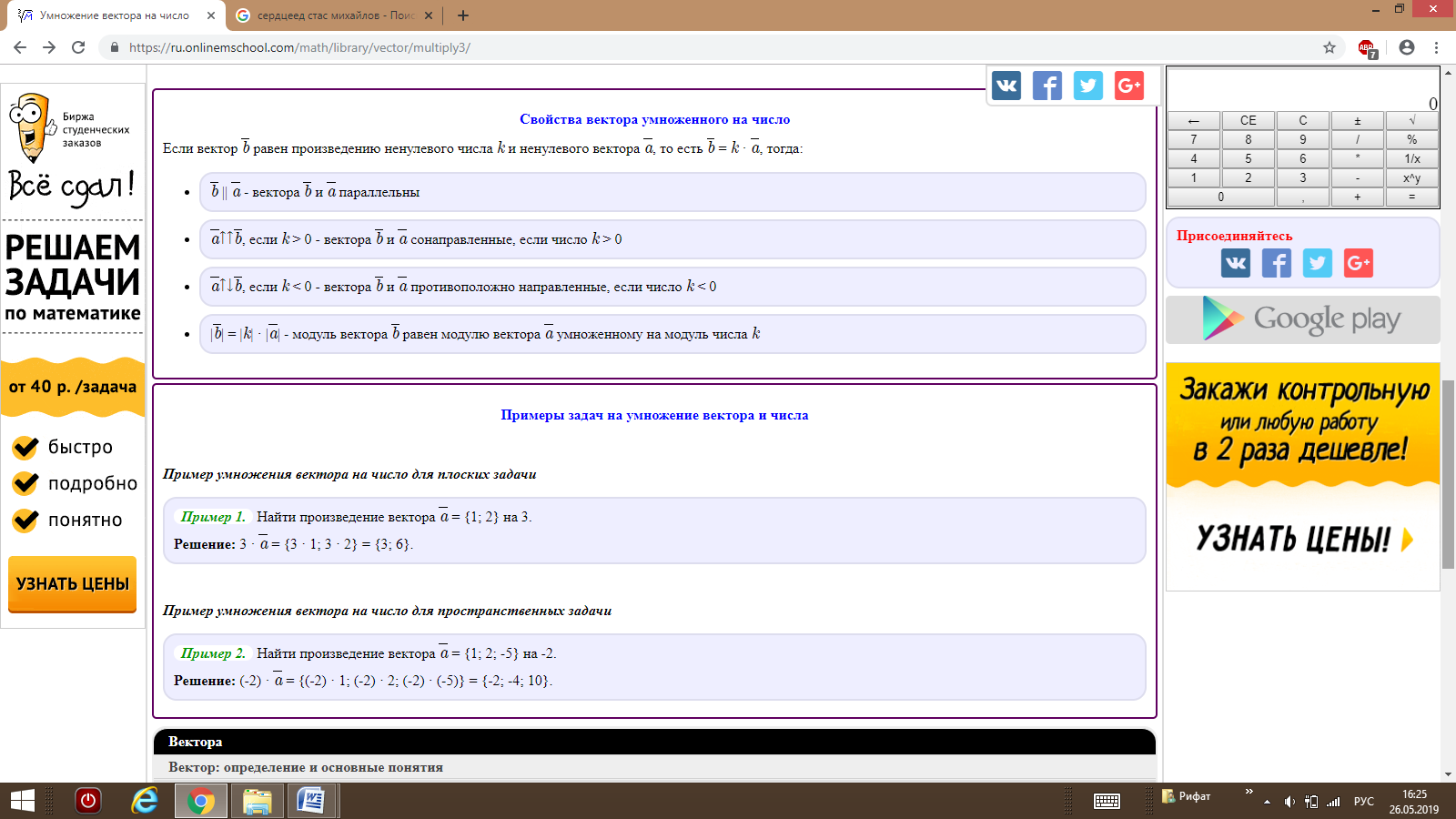
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

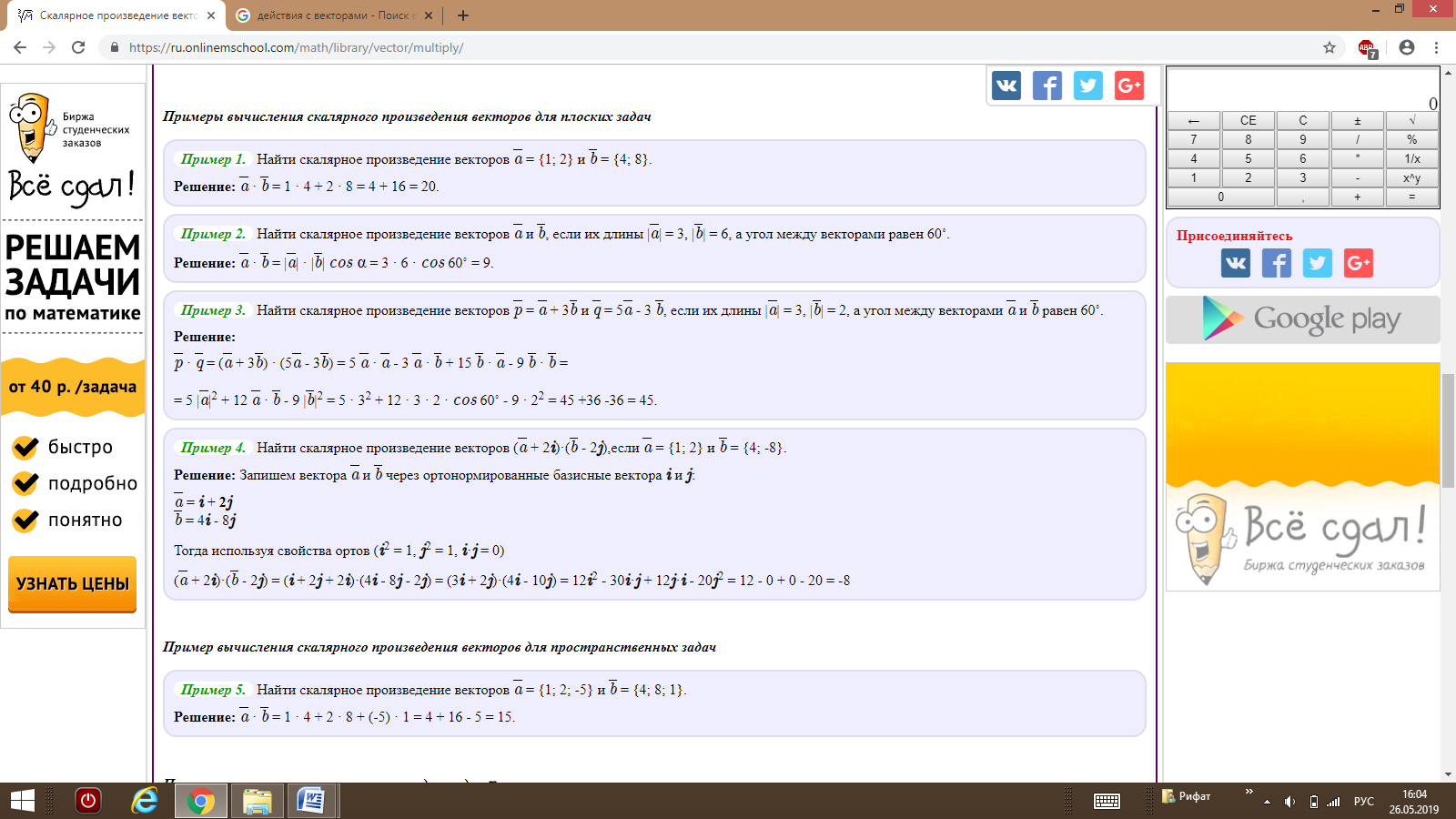
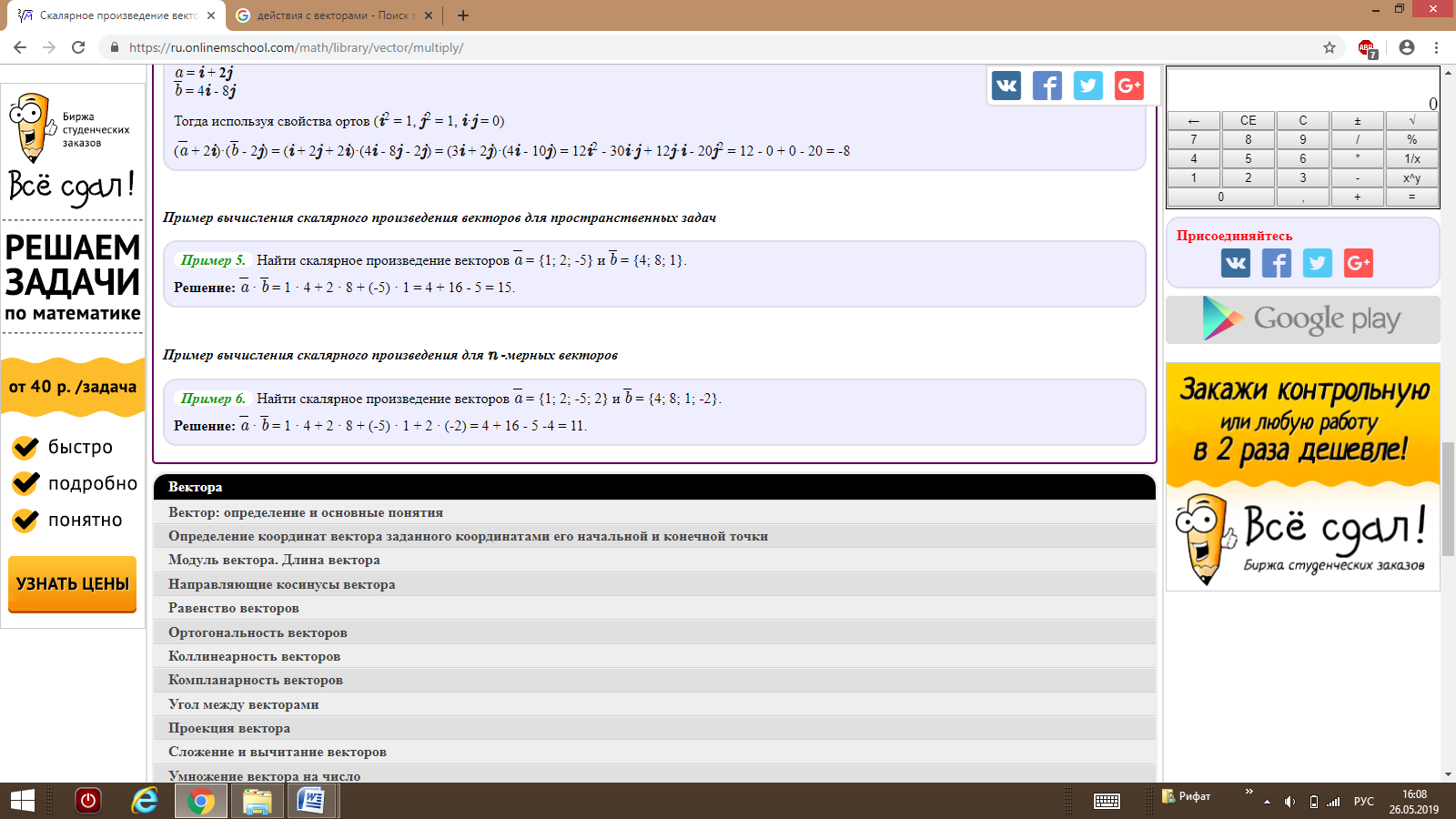
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A ₁ B ₁ оси l , где точки A ₁ и B ₁ являются проекциями точек A и B на ось l . (рис. 1).

Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b .

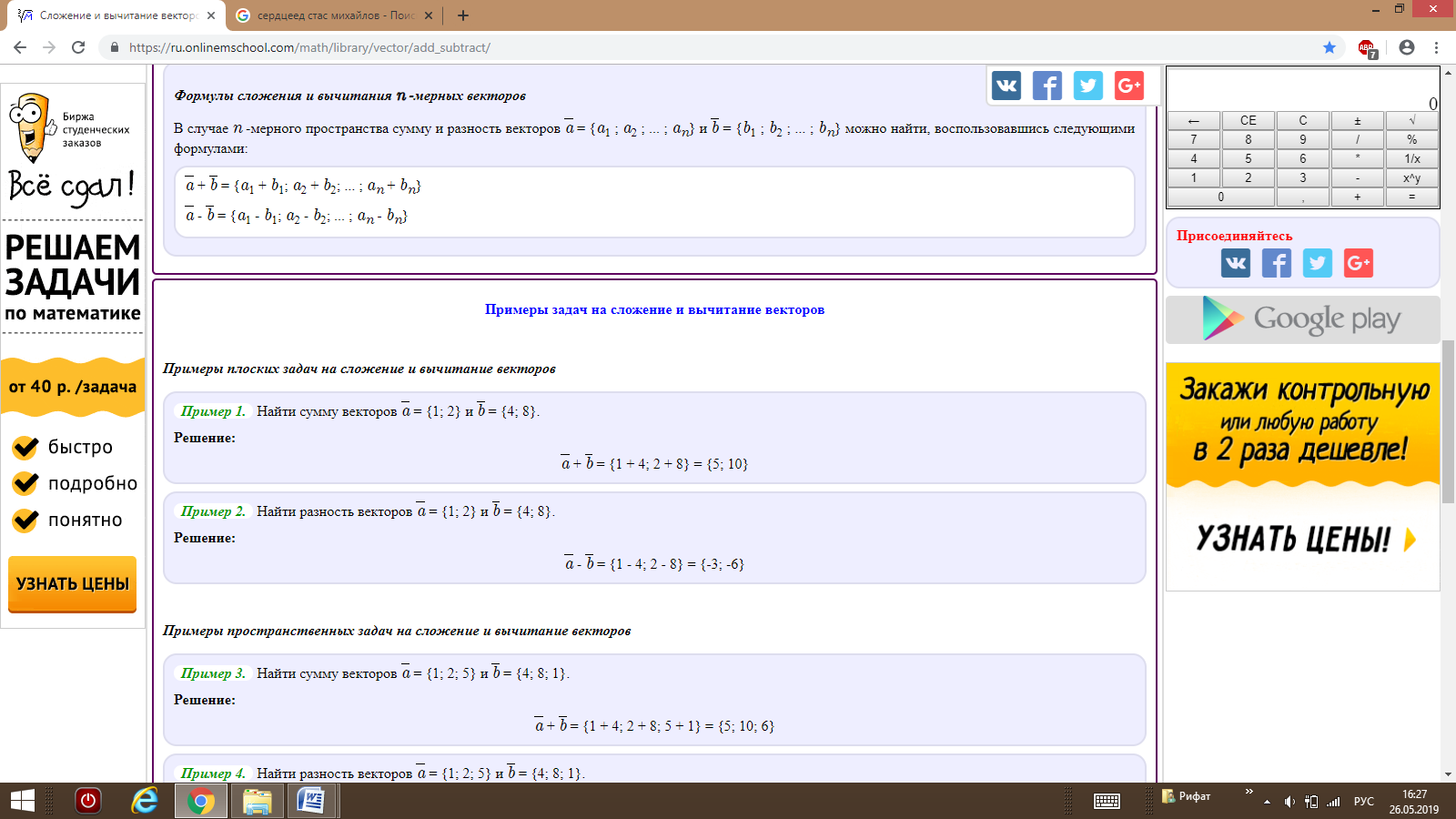
Примеры задач на равенство векторов

Примеры плоских задач на равенство векторов

a = b — так как их координаты равны, a ≠ c — так как их координаты не равны, b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов a_x = b_x = 1 a_y = b_y => 8 = 2 n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

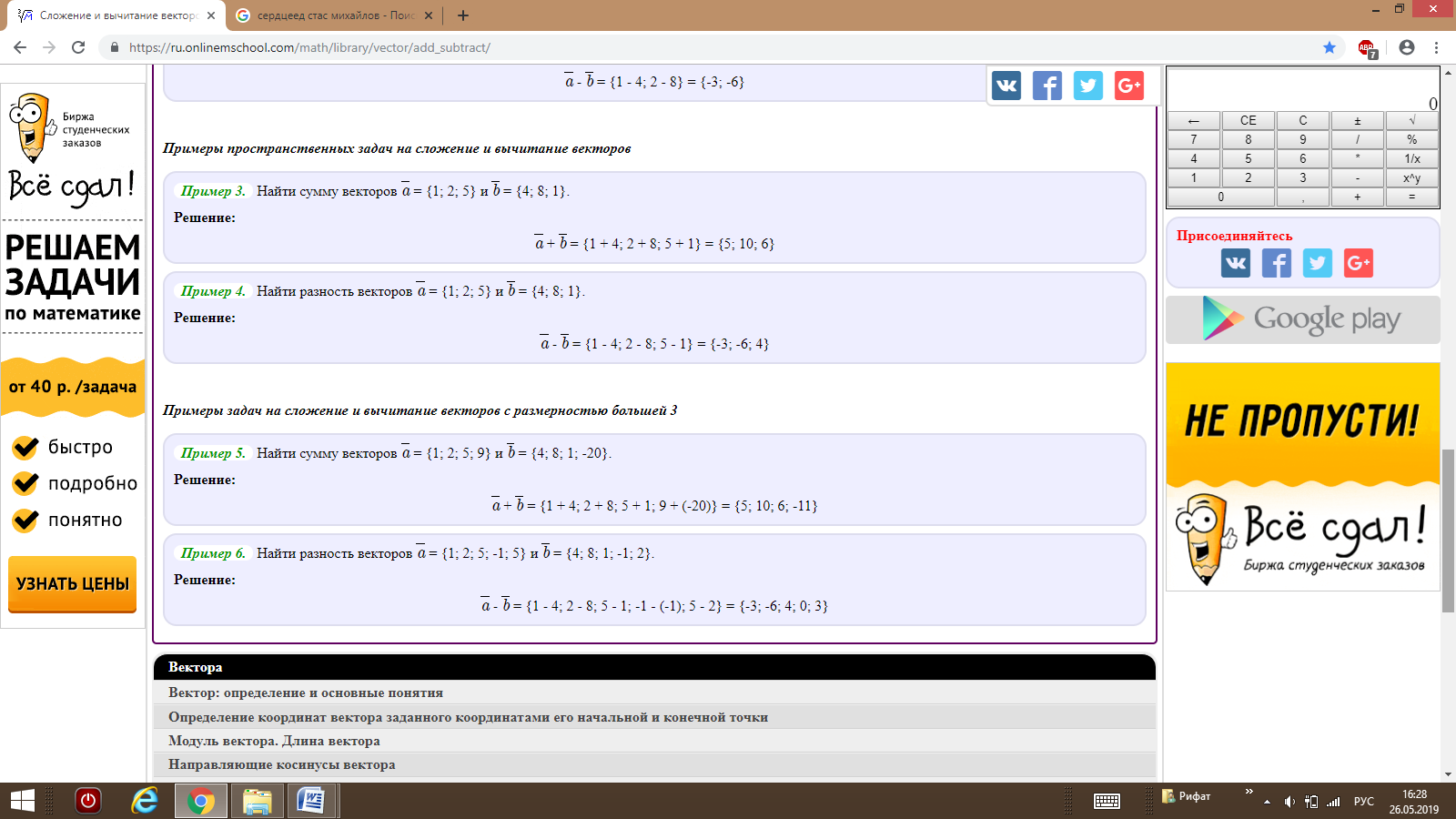
Примеры пространственных задач на равенство векторов

a = c — так как их координаты равны, a ≠ b — так как их координаты не равны, b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов a_x = b_x = 1 a_y = b_y = 2 a_z = b_z => 4 = 2 n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Примеры задач на проекцию вектора

Примеры вычисления проекции вектора для плоских задач

Пример 1. Найти проекцию вектора a = на вектор b = .

Найдем скалярное произведение этих векторов

a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11

Найдем модуль вектора b

| b | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5

Найдем проекцию вектора a на вектор b

Примеры вычисления проекции вектора для пространственных задачи

Пример 2. Найти проекцию вектора a = на вектор b = .

Найдем скалярное произведение этих векторов

a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12

Найдем модуль вектора b

| b | = √ 4 2 + 2 2 + 4 2 = √ 16 + 4 + 16 = √ 36 = 6

Найдем проекцию вектора a на вектор b

Курс повышения квалификации

Сейчас обучается 935 человек из 80 регионов

Курс повышения квалификации

Сейчас обучается 316 человек из 70 регионов

Курс профессиональной переподготовки

Сейчас обучается 696 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Свойства равенства векторов

1. Рефлексивность: Вектор всегда равен самому себе. То есть, для любого вектора а выполняется условие: а = а.

2. Симметричность: Если векторы а и b равны, то их порядок не имеет значения. То есть, если а = b, то b = а.

3. Транзитивность: Если векторы а, b и c равны, то можно сделать вывод, что векторы а и c также равны. То есть, если а = b и b = c, то а = c.

4. Добавление нулевого вектора: Добавление нулевого вектора к любому вектору не изменяет его. То есть, для любого вектора а выполняется условие: а + 0 = а.

5. Обратный вектор: У каждого вектора существует обратный вектор, который при сложении с ним дает нулевой вектор. То есть, для любого вектора а существует вектор -а, такой что а + (-а) = 0.

6. Коммутативность сложения: Порядок слагаемых при сложении векторов не имеет значения. То есть, для любых векторов а и b выполняется условие: а + b = b + а.

7. Ассоциативность сложения: При сложении трех и более векторов, порядок их группировки не имеет значения. То есть, для любых векторов а, b и с выполняется условие: (а + b) + с = а + (b + с).

8. Умножение на скаляр: Умножение вектора на скаляр равносильно умножению каждой его компоненты на этот скаляр. То есть, для любого вектора а и скаляра α выполняется условие: α*а = (α*a₁, α*a₂, …, α*a_n).

9. Дистрибутивность умножения на скаляр относительно суммы векторов: Умножение суммы векторов на скаляр равносильно сумме умножений каждого вектора на этот скаляр. То есть, для любых векторов а, b и скаляра α выполняется условие: α*(а + b) = α*а + α*b.

Понятие вектора

Иногда, к примеру, в физике, для характеристики некоторых величин необходимо не только их числовое значение, но и направление (скорость, ускорение, сила…). Такие величины называются векторными величинами или коротко векторами. Напомним, что величины, не требующие направления, называются скалярными величинами.

Для введения понятия геометрического вектора будем использовать понятие отрезка. Введем следующее определение.

Определение 1

Граничные точки отрезка — это концы отрезка.

Отрезок может иметь два направления. Для обозначения направления будем называть одну граничную точку отрезка началом, а другую концом. Направление будет указываться от начала отрезка к его концу.

Определение 2

Вектором или направленным отрезком называется отрезок, для которого указано, какая из граничных точек считается началом, а какая концом данного отрезка.

Обозначение: $\overrightarrow{AB}$ — вектор $AB$ с началом в точке $A$ и концом в точке $B$.

Также вектор может обозначаться одной маленькой буквой: $\overrightarrow{a}.$

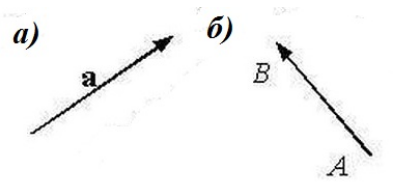Рисунок 1. Примеры векторов: а) вектор $\overrightarrow{a}$; б) вектор $\overrightarrow{AB}$.

Введем еще несколько понятий, связанных с понятием вектора.

Определение 3

Нулевым вектором называется любая точка плоскости.

Обозначение: $\overrightarrow{0}$.

Определение 4

Длиной или модулем вектора $\overrightarrow{a}$ называется длина отрезка $a.$

Обозначение: $|\overrightarrow{a}|$

Замечание 1

Отметим, что длина нулевого вектора равна нулю: $\left|\overrightarrow{0}\right|=0$.

равных векторов

Навигация по странице:

• Равные векторы — определение
• Условия равенства векторов
• Примеры задач
  • плоские задачи
  • пространственных задач

Определение.

равными векторами

Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину:

Условия равенства векторов. Векторы равны , если их координаты равны.

Рис. 1

Примеры плоских задач

Пример 1. Определить, какие из векторов равны a = {1; 2}, б = {1; 2}, с = {3; 2}.

Решение:

a = b — так как их координаты равны, a ≠ c — так как их координаты не равны, b ≠ c — так как их координаты не равны.

Пример 2. При каком значении параметра n векторы a = {1; 8;} и b = {1; 2n} равны.

Решение:

Проверить равенство компонентов векторов а _х = б _х = 1 _г = b _y => 8 = 2n => n = 8/2 = 4

Ответ: при n = 4 векторы a и b равны.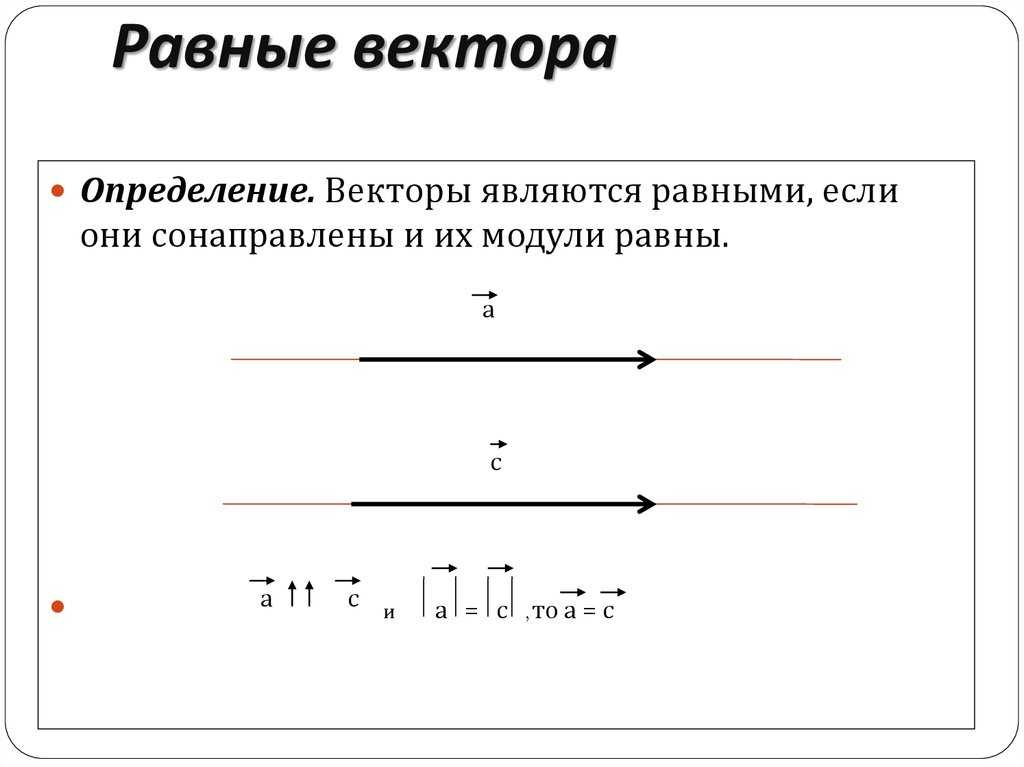

Примеры пространственных задач

Решение:

a = c — так как их координаты равны, a ≠ b — так как их координаты не равны, b ≠ c — так как их координаты не равны.

Пример 4. При каком значении параметра n векторы a = {1; 2; 4} и б = {1; 2; 2n} равны.

Решение:

Проверить равенство компонентов векторов а _х = б _х = 1 а _у = б _у = 2 a _z = b _z => 4 = 2n => n = 4/2 = 2

Векторы
Определение векторов. Основная информация
Компонентная форма вектора с начальной и конечной точками
Длина вектора
Направленные косинусы вектора
Равные векторы
Ортогональные векторы
Коллинеарные векторы
Компланарные векторы
Угол между двумя векторами
Векторная проекция
Сложение и вычитание векторов
Скалярно-векторное умножение
Скалярное произведение двух векторов
Перекрестное произведение двух векторов (векторное произведение)
Скалярное тройное произведение (смешанный продукт)
Линейно зависимые и линейно независимые векторы
Разложение вектора по базису

Онлайн калькуляторы с векторами

Задания и упражнения с вектором 2D

Векторы в тетраэдре, решение задачи

Задача 2

Задан тетраэдр  с вершиной  и основанием . Точка  – середина ребра , точка  – середина ребра , точка  – середина ребра , точка  – середина ребра . Обозначены векторы , , , ,  и . Выпишите все пары равных векторов из обозначенных на рисунке. Определите вид четырехугольника .

Рассмотрим чертеж (рис. 6):

Рис. 6. Тетраэдр

Для начала рассмотрим четырехугольник  без учета векторов. Отметим, что  и  как средняя линия треугольника . Аналогично  и  как средняя линия треугольника . Имеем:

по свойству транзитивности.

Так, в четырехугольнике  две противоположные стороны параллельны и равны, нам известен соответствующий признак: если в четырехугольнике две противоположные стороны параллельны и равны, то такой четырехугольник – параллелограмм. Имеем:  – параллелограмм.

Теперь мы можем заключить равенство и параллельность отрезков  и , причем как сторон параллелограмма, так и средних линий для треугольников  и  соответственно.

Перейдем к равенству векторов:

 и , т. к. противоположные стороны параллелограмма принадлежат параллельным прямым (векторы коллинеарны и сонаправлены) и равны по длине.

, т. к. они принадлежат одной прямой (коллинеарны и сонаправлены) и равны по длине (точка  – середина ребра ).

, т. к. они принадлежат одной прямой (коллинеарны), противонаправлены и длины их равны (точка  – середина ребра ).

          Итак, мы ввели понятие вектора в пространстве, рассмотрели основные определения, касательно векторов в пространстве, рассмотрели равенство векторов и длины векторов в наиболее распространенных геометрических фигурах – прямоугольном параллелепипеде и тетраэдре.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/vektory-v-prostranstve/ponyatie-vektora-ravenstvo-vektorov

https://www.youtube.com/watch?v=bYEnByZUm04

http://v.5klass.net/zip/57bddfe89e626d9d10ec396f887885ec.zip

http://www.mathprofi.ru/vektory_dlya_chainikov.html

http://www.bookle.ru/cover/223895.jpg

Как найти вектор, коллинеарный вектору

Вы будете перенаправлены на Автор24

Понятие коллинеарности векторов

Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Обозначение: $overline$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline$ (рис. 1).

Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Далее рассмотрим, какие векторы называются коллинеарными.

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).

Готовые работы на аналогичную тему

Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ

Также введем определение векторного произведения, которое будет нам необходимо далее.

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Чтобы найти векторное произведение, будем пользоваться формулой

$overlineхoverline=beginoverline&overline&overline\α_1&α_2&α_3\β_1&β_2&β_3end$

Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.

Доказательство.

Необходимость: Пусть нам даны векторы $overline$ и $overline$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $overline$ и $overline$ будут коллинеарными.

Из данных равенств следует, что $roverline=overline$.

Имеются два случая:

Тогда, в обоих случаях получаем доказательство коллинеарности векторов $overline$ и $overline$.

Ответ: теорема доказана.

Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.

Доказательство.

Разложим второй вектор:

Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.

Признаки и свойства коллинеарности векторов через их произведение

Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.

Доказательство.

Необходимость: Пусть нам даны векторы $overline$ и $overline$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать, что $overlineхoverline=overline$.

Так как векторы коллинеарны, то, по теореме 1, верны равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Найдем $overlineхoverline$ по формуле

$overlineхoverline=beginoverline&overline&overline\α_1&α_2&α_3\β_1&β_2&β_3end=beginoverline&overline&overline\rβ_1&rβ_2&rβ_3\β_1&β_2&β_3end=rbeginoverline&overline&overline\β_1&β_2&β_3\β_1&β_2&β_3end=rcdot overline=overline$

Достаточность: Пусть верно равенство $overlineхoverline=overline$, докажем, что векторы $overline$ и $overline$ коллинеарны. Так как векторное произведение равняется $overline$, то его длина также равняется нулю. Следовательно, угол между $overline$ и $overline$ равняется $180^circ$ или $0^circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.

Равенство векторов

Через начало и конец векторов можно провести прямую. В связи с этим можно ввести понятие коллинеарных векторов.

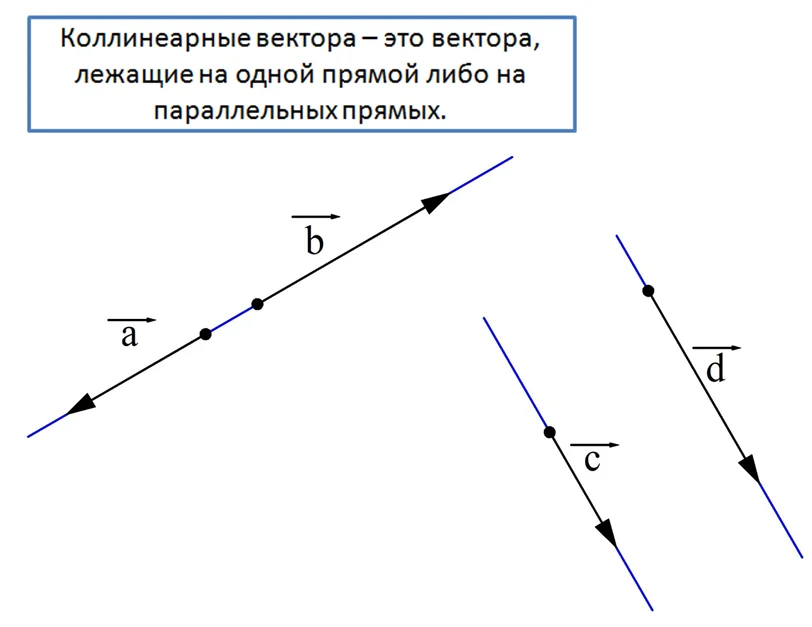
На рисунке коллинеарны вектора а и b, так как они лежат на одной прямой. Также коллинеарны с и d, так как они лежат на параллельных прямых. А вот вектора a и c неколлинеарны, так как они лежат на пересекающихся прямых.

Для пары коллинеарных векторов можно определить, являются ли они сонаправленными или противоположно направленными.

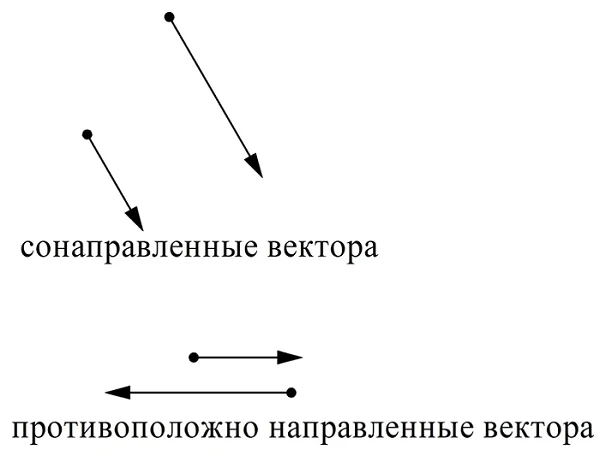
Для обозначения сонаправленных векторов используется символ «⇈», а для противоположно направленных «⇅». Можно сформулировать две очевидных теоремы о коллинеарных векторах.

Проиллюстрируем эти правила с помощью рисунка:

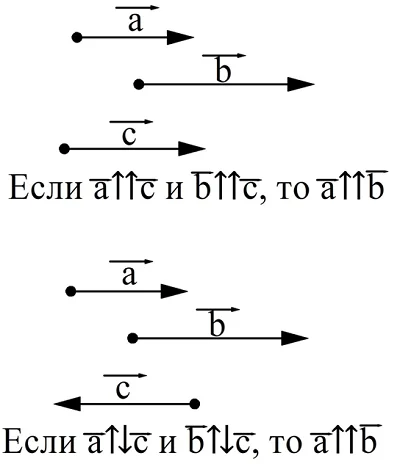
Особняком стоит нулевой вектор. Он представляет собой точку, а потому не имеет определенного направления. Поэтому условно его считают сонаправленным с любым другим вектором.

Теперь мы можем дать определение равенству векторов.

Задание. Найдите на картинке равные вектора.

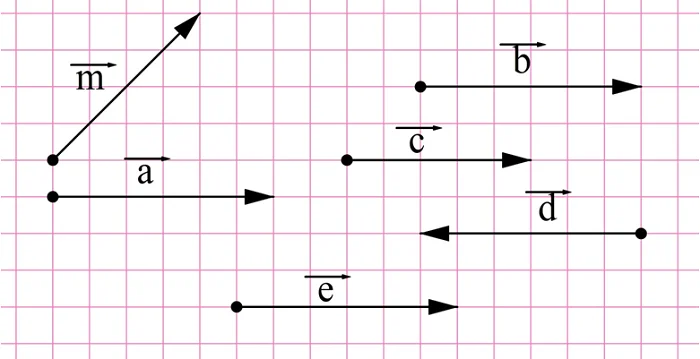
Решение. Здесь равны вектора а, b и e. Они сонаправлены и имеют длину 6. Вектор с сонаправлен с ними, но его длина составляет только 5 клеток. Длина вектора d составляет 6 клеток, но он не сонаправлен с другими векторами. Наконец, вектор m также не сонаправлен с другими векторами и даже не коллинеарен им.

Ответ: a, b и e.

Если началом вектора является некоторая точка А, то можно сказать, что вектор отложен от точки А

Докажем важное утверждение:

Доказать его можно построением. Пусть есть вектор а и точка М. Проведем через М прямую p, параллельную вектору а. Такая прямая будет единственной. Если точка М и вектор лежат на одной прямой, то в качестве прямой p возьмем именно эту прямую. Далее от точки М можно отложить отрезки МN и МN’, длина которых будет совпадать с длиной вектора а. В результате получится два вектора,MN и MN’, один из которых будет сонаправлен с а, а другой – противоположно направленный.

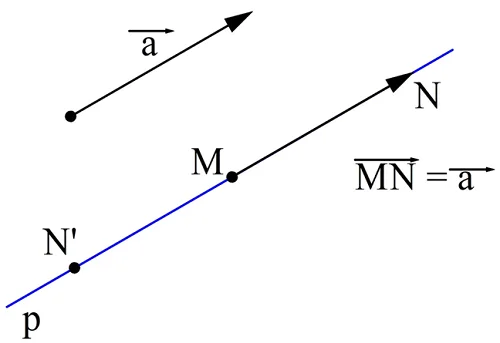
Часто равные вектора, отложенные от разных точек, обозначают одной буквой. Можно считать, что это один и тот же вектор, просто приложенный к разным точкам.

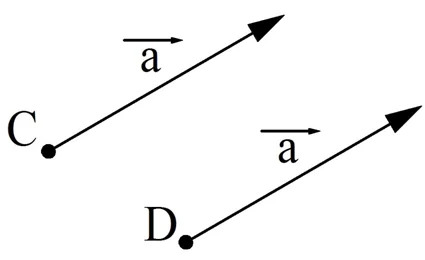
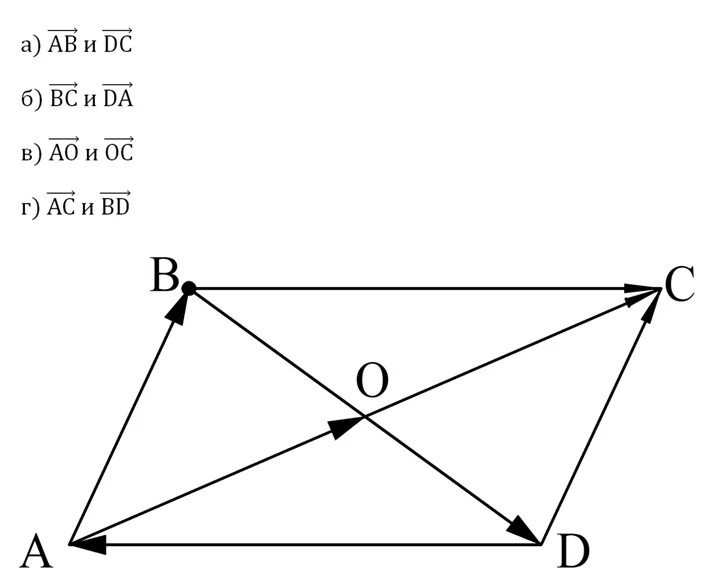
Задание. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Определите, равны ли вектора:

Решение.

а) Отрезки АВ и DC равны, ведь это противоположные стороны параллелограмма, по той же причине эти отрезки параллельны. Видно, что они сонаправлены, значит, вектора равны.

б) Отрезки ВС и DA параллельны и равны, но эти вектора противоположно направлены, поэтому вектора НЕ равны друг другу.

в) Точка пересечения диагоналей параллелограмма делит их пополам, поэтому длины отрезков АО и ОС одинаковы. Вектора АО и ОС лежат на одной прямой, то есть они коллинеарны. При этом они ещё и сонаправлены, поэтому АО и ОС – равные векторы.

г) Вектора АС и BD лежат на пересекающихся прямых, то есть они не коллинеарны. Этого уже достаточно, чтобы считать их НЕ равными друг другу.

Ответ: а) д; б) нет; в) да; г) нет.

21 Условие перпендикулярности векторов

Если
ненулевые векторы

= (x₁; y₁;
z₁) и

= (x₂; y₂;
z₂) перпендикулярны, то их
скалярное произведение равно нулю

=
0,

=
x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Если
задан один ненулевой вектор

= (x₁; y₁;
z₁), то координаты
перпендикулярного (нормального) ему ненулевого
вектора

= (x₂; y₂;
z₂) должны удовлетворять
равенству

x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Таких
векторов

бесконечное множество.

Если
на плоскости задан один ненулевой вектор

= (x₁; y₁),
то координаты перпендикулярного (нормального) ему вектора

= (x₂; y₂)
должны удовлетворять равенству

x₁x₂
+ y₁y₂
= 0.

Отсюда
можно выразить произведение координат y

y₁y₂
= — x₁x₂.

Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то достаточно задать произвольно одну из координат перпендикулярного
(нормального) ему вектора

= (x₂; y₂)
и из условия перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

выразить
вторую координату вектора

.

Например,
если подставить произвольную координату x₂,то из равенства

y₁y₂
= — x₁x₂

выражается
вторая координата вектора

Если
произвольно придать x₂ = y₁,
то вторая координата вектора

Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то перпендикулярный (нормальный) ему вектор

= (y₁; -x₁).

Если
одна из координат ненулевого вектора

равна нулю, то у перпендикулярного ему ненулевого вектора

такая же координата не равна нулю, а вторая координата равна нулю.
Такие векторы лежат на осях координат, поэтому перпендикулярны.
Например, если

= (; y₁),
то этот вектор лежит на оси Oy, тогда
перпендикулярный ему ненулевой вектор

= (x₂;
0) лежит на оси Ox.

Определим
второй вектор, перпендикулярный вектору

= (x₁; y₁),
но противоположный вектору

= (y₁; -x₁),
то есть вектор —
.
Тогда достаточно поменять знаки координат вектора

—

= -1·

= (-1·y₁;
-1·(-x₁))=
(-y₁; x₁).

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Для
получения координат ненулевых векторов, перпендикулярных заданному
ненулевому вектору на плоскости, достаточно поменять местами
координаты заданного вектора и поменять знак одной из координат.

Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Подставляем
координаты вектора

= (3; -5)

₁
= (-5; -3),

₂
= (-(-5); 3) = (5; 3).

Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·(-5)
+ (-5)·(-3) = -15 + 15 = 0

верно!

3·5
+ (-5)·3 = 15 — 15 = 0

верно!

Ответ:
₁
= (-5; -3),
₂
= (5; 3).

Если
присвоить x₂ = 1, подставить

x₁
+ y₁y₂
= 0.

y₁y₂
= -x₁

Получим
координату y₂ вектора,
перпендикулярного вектору

= (x₁; y₁)

Координаты
одного вектора, перпендикулярного на плоскости ненулевому вектору

= (x₁; y₁)

Для
получения второго вектора, перпендикулярного вектору

= (x₁; y₁),
но противоположно направленного вектору

.
Пусть

Тогда
достаточно поменять знаки координат вектора

.

Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

Координаты
одного вектора

Координаты
второго вектора

Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·1
+ (-5)·0,6 = 3 — 3 = 0

верно!

3·(-1)
+ (-5)·(-0,6) = -3 + 3 = 0

верно!

Ответ:

и

.

Если
присвоить x₂ = — x₁,
подставить

x₁(-x₁)
+ y₁y₂
= 0.

-x₁2
+ y₁y₂
= 0.

y₁y₂
= x₁2

Получим
координату вектора, перпендикулярного вектору

Если
присвоить x₂ = x₁,
подставить

x₁x₁
+ y₁y₂
= 0.

x₁2
+ y₁y₂
= 0.

y₁y₂
= -x₁2

Получим
координату y второго вектора,
перпендикулярного вектору

Координаты
одного вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

Слайд 6Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного

исчисления и его приложений. Были созданы векторная алгебра и векторный

анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.

Базис.

Ранее было дано определение . Введем теперь определение базиса.

Определение.

Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается.

Из доказанной выше сразу вытекает, что

• В нулевом пространстве базиса не существует.
• В одномерном пространстве (на прямой линии) базис состоит из одного ненулевого вектора.
• В двумерном пространстве (на плоскости) базис — упорядоченная пара неколлинеарных векторов.
• В трехмерном пространстве базис — упорядоченная тройка некомпланарных векторов.

Требование упорядоченности означает, что, например, в случае плоскости \(\boldsymbol{a}\), \(\boldsymbol{b}\) и \(\boldsymbol{b}\), \(\boldsymbol{a}\) — два разных базиса.

Так как векторы базиса линейно независимы, коэффициенты разложения по базису для каждого вектора пространства определены однозначно. Они называются компонентами или координатами вектора в этом базисе.

Таким образом, если \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\) — базис трехмерного пространства, то по формуле \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) каждому вектору сопоставлена единственная упорядоченная тройка чисел \(\alpha_{1}\), \(\alpha_{2}\), \(\alpha_{3}\) и каждой тройке чисел — единственный вектор. Аналогично, вектор на плоскости имеет две компоненты, а на прямой — одну.

Компоненты пишутся в скобках после буквенного обозначения вектора, например \(\boldsymbol{a}\)(1,0,1).

В аналитической геометрии геометрические рассуждения о векторах сводятся к вычислениям, в которых участвуют компоненты этих векторов. Следующее предложение показывает, как производятся линейные операции над векторами, если известны их компоненты.

Утверждение 5.

При умножении вектора на число все его компоненты умножаются на это число. При сложении векторов складываются их соответствующие компоненты.

Действительно, если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\), то

$$
\lambda\boldsymbol{a} = \lambda(\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) = (\lambda\alpha_{1})\boldsymbol{e_{1}} + (\lambda\alpha_{2})\boldsymbol{e_{2}} + (\lambda\alpha_{3})\boldsymbol{e_{3}}.\nonumber
$$
Если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) и \(\boldsymbol{b} = \beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}\), то

$$
\boldsymbol{a} + \boldsymbol{b} = (\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) + (\beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}) =\\= (\alpha_{1} + \beta_{1})\boldsymbol{e_{1}} + (\alpha_{2} + \beta_{2})\boldsymbol{e_{2}} + (\alpha_{3} + \beta_{3})\boldsymbol{e_{3}}.\nonumber
$$

Для одномерного и двумерного пространств доказательство отличается только числом слагаемых.

Сложение и вычитание векторов

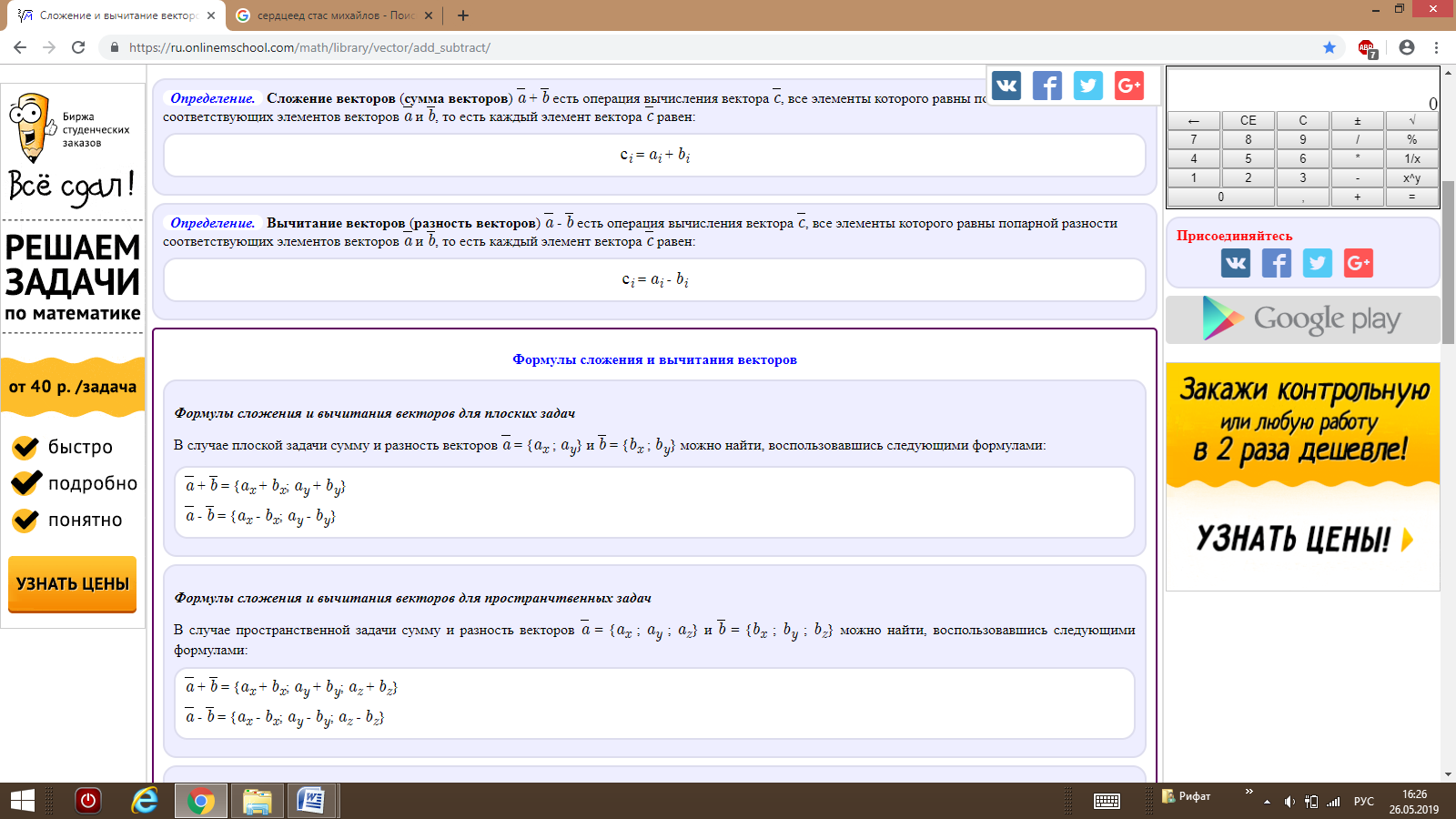
      Для того, чтобы найти сумму двух произвольных векторов     и     нужно совместить начало вектора     с концом вектора   .   Тогда началом вектора     будет начало вектора   ,   а концом вектора     будет конец вектора     (рис.9).

Рис.9

      При этом, если

      и      

то

      Этот факт часто формулируют так: «При сложении векторов их координаты складываются».

      Для того, чтобы найти разность двух произвольных векторов     и     нужно воспользоваться формулой

      Операция вычитания двух векторов наглядно изображена на рисунке 10.

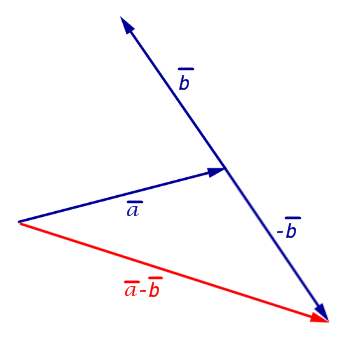
Рис.10

      При этом, если

      и      

то

      Этот факт часто формулируют так: «Для того, чтобы найти координаты вектора   ,   нужно из координат вектора     вычесть координаты вектора   ».

Равные векторы

В различных школьных учебниках определение равных векторов даётся по-разному.

В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.

Два вектора называются равными, если они совмещаются параллельным переносом.

(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Например, изображенные на рисунке

Равенство векторов обозначают так:

(Свойства равных векторов)

1) Равные векторы сонаправлены и имеют равные длины.

2) Равные векторы имеют равные координаты.

3) От любой точки можно отложить вектор, равный данному, и притом только один.

1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.

2) Пусть дан вектор

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂).

По определению равных векторов, вектор

равный данному, получен из

Если этот параллельный перенос задан формулами

Найдём координаты каждого из векторов:

То есть координаты равных векторов

Что и требовалось доказать.

Таким образом, координаты задают длину и направление вектора, но не фиксируют его.

3) Пусть даны вектор

и точка C. Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор

При таком параллельном переносе вектор

переходит в вектор

По определению равных векторов,

Что и требовалось доказать.

На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).

Например,

отложенный от точки C, равен вектору

(Признаки равенства векторов)

1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.

2) Если у векторов соответствующие координаты равны, то векторы равны.

1) Пусть векторы

сонаправлены и имеют одинаковые длины.

Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор

переводит в вектор

По определению равных векторов,

Что и требовалось доказать.

2) Пусть векторы

Параллельный перенос, заданный формулами

переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы

А это означает, что

Что и требовалось доказать.

В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.

Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.