Как найти площадь окружности если известен сектор

Формула (формулы) площади круга

Найти площадь круга можно разными способами, в зависимости от известных данных.

По радиусу

Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):

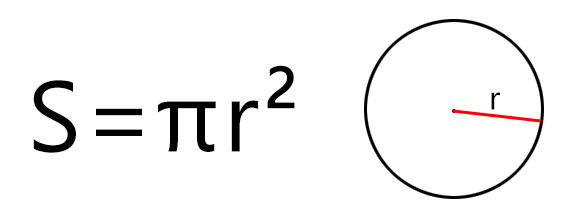
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).

Через диаметр

Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):

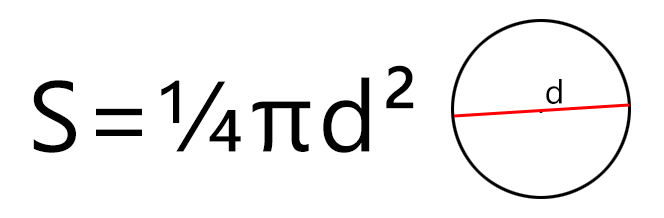
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).

Через длину окружности

Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):

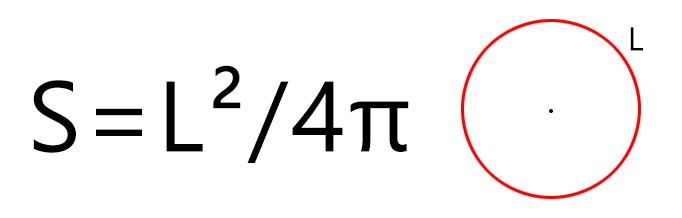
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202  / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).

Почему площадь круга равна числу пи в квадрате

Вы, вероятно, уже знаете, что площадь круга можно вычислить по формуле S = πr², где r — радиус круга, а π — математическая константа, примерное значение которой равно 3,1415926535…

Так почему же площадь круга равна числу π в квадрате? Это связано с тем, что сама константа π является отношением длины окружности к ее диаметру.

Точная природа π до сих пор остается загадкой для математиков, их теоретический интерес заполняет бесконечное количество книг, однако интуитивная идея заключается в том, что длина окружности и ее радиус связаны с точкой, расположенной на окружности, поправив ее на 90 градусов.

Таким образом, мы можем вывести уравнение окружности, зная ее радиус. И, используя эту информацию, мы можем вычислить ее площадь, умножив π на квадрат радиуса.

Таким образом, площадь круга зависит от радиуса, который связан с длиной окружности через константу π. Именно поэтому площадь круга равна числу π в квадрате.

Площадь сектора при неизвестном радиусе

Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.

Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:

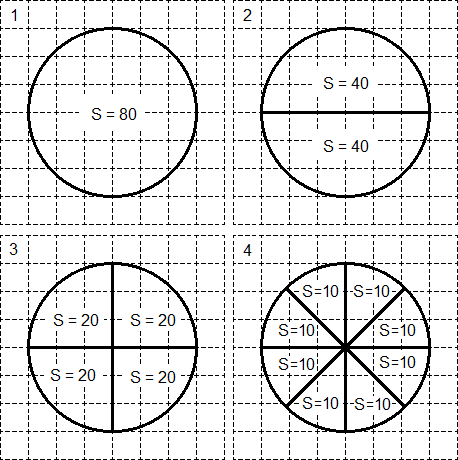
Пусть исходный круг имеет площадь S
круга = 80. Тогда его можно разделить на два сектора площадью S
= 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S
= 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S
= 10.

Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:

1. Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
   круга = 240, то «ошметки» имеют площадь S
   = 240: 8 = 30;
2. Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S
   = 3 · 30 = 90. Это и будет ответ.

Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.

А теперь разберем примеры из пробного ЕГЭ:

Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S
= 40: 5 = 8. Получим:

Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!

Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S
= 64: 8 = 8.

Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S
= 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.

• Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
• Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности
  к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.

Длина окружности

Рассмотрим – угольникnправильный     B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2

Поскольку – угольникаnплощадь   B1B2…Bn   равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

Следствие. Длина окружности радиуса 1 равна   2π.

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

l=πd, где

π— число пи — математическая константа, равная 3,14

d — диаметр окружности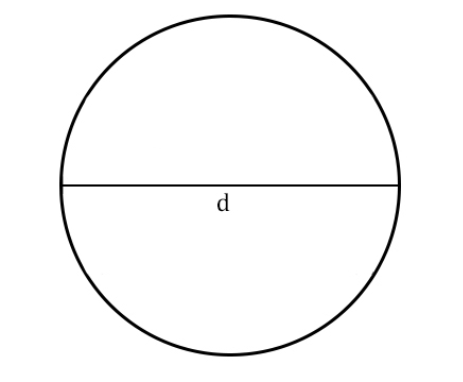

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

l=2πr , где

π — число пи, равное 3,14

r — радиус окружности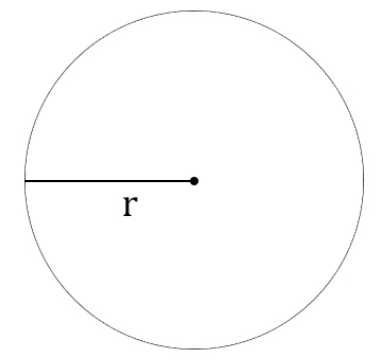

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

где:

• π — число пи, равное 3,14
• S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник: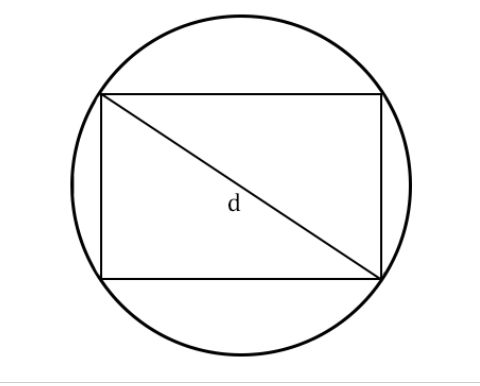

l=πd, где

• π — число пи, равное 3,14
• d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата: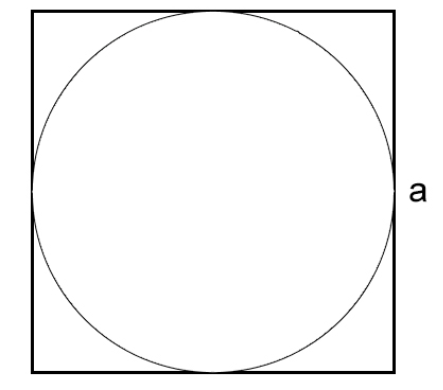

l=πa, где

• π — математическая константа, равная 3,14
• a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:

• π — математическая константа, она всегда равна 3,14
• a — первая сторона треугольника
• b — вторая сторона треугольника
• c — третья сторона треугольника
• S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:

• π — математическая константа, равная 3,14
• S — площадь треугольника
• p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:

где:

• π — математическая константа, равная 3,14
• a — сторона многоугольника
• N — количество сторон многоугольника

Как вычислить площадь круга с диаметром

••• mr.suphachai praserdumrongchai/iStock/GettyImages

Обновлено 16 ноября 2020 г. , но изучение математических понятий диаметра и площади иногда может показаться сложным. Независимо от того, измеряете ли вы размер круглого ковра, который вам нужно купить, или определяете пространство, необходимое для строительства круглого сада или патио, знание того, как рассчитать площадь круга по его диаметру, является ценным навыком.

TL;DR (слишком длинно, не читал)

Площадь круга — это площадь, которую занимает круг. Формула для вычисления площади круга: A = π r 2 , где пи (π) равно 3,14, а радиус ( r ) равен половине диаметра.

Первым шагом для вычисления площади круга по его диаметру является определение этого диаметра. В то время как математические задачи часто указывают это значение, в реальном мире вы должны найти диаметр самостоятельно.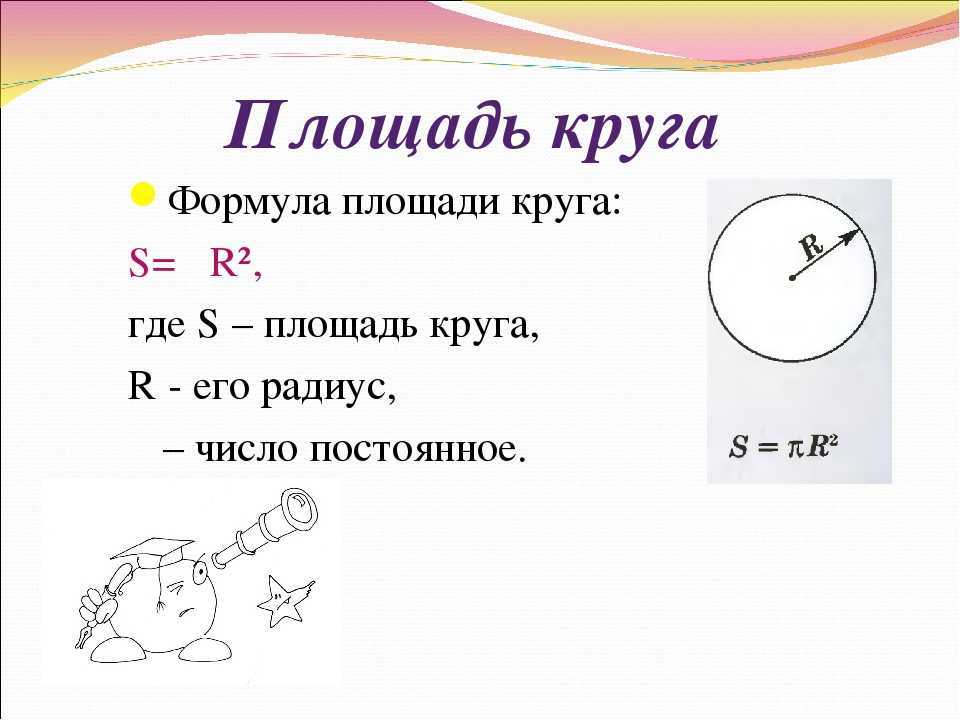

Диаметр — это длина линии, которая начинается на краю круга, проходит через центр круга и заканчивается на противоположном краю круга. Для измерения вам понадобится линейка для маленьких кругов или рулетка для больших кругов.

Зная диаметр (​ d ​) окружности, вы можете найти радиус (​ r ​), используя уравнение ​ d ​=2​ r ​. Радиус круга — это расстояние от центра круга до любой точки на краю круга. Радиус также равен половине диаметра. Если ваш диаметр представляет собой простое число, вы, вероятно, можете вычислить радиус в уме. Если нет, измените уравнение, чтобы найти ​ r ​

r = \frac{d}{2} 92

Пи (π) — неалгебраическое число, представляющее отношение расстояния по окружности (окружности) к ее диаметру, обычно оцениваемое как 3,14. Чтобы найти площадь, возведите радиус в квадрат (радиус умножить на радиус), а затем умножьте на 3,14.

Поскольку площадь является мерой двух измерений, вы всегда указываете площадь в квадратных единицах, таких как квадратные дюймы (в 2 ) или квадратные футы (футы 2 ).

Это особенно важно при расчете площади круга для задания, поскольку ответ без правильно сообщенных единиц измерения, скорее всего, будет неправильным или неполным. Каждый раз, когда вам нужно определить пространство внутри круга или количество пространства, покрываемого кругом, вы можете использовать уравнение для площади круга

Особенно для реальных приложений этого навыка измерение диаметра часто является самым простым способом начать

Каждый раз, когда вам нужно определить пространство внутри круга или количество пространства, покрываемого кругом, вы можете использовать уравнение для площади круга. Особенно для реальных приложений этого навыка измерение диаметра часто является самым простым способом начать.

Ссылки

• Академия Хана: площадь и периметр
• Забавная математика: площадь круга

Ресурсы

Живая наука: что такое число Пи?

Об авторе

Мелисса Майер — разноплановый научный писатель с опытом работы в области молекулярной биологии, протеомики, геномики, микробиологии, биобанкинга и пищевой науки. В нише научных и медицинских текстов ее работа включает пять лет работы с Thermo Scientific (ускорение научных блогов), SomaLogic, Mental Floss, Society for Neuroscience и Healthline.

Формулы для нахождения площади круга, его сегмента или сектора

В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:

Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.

Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:

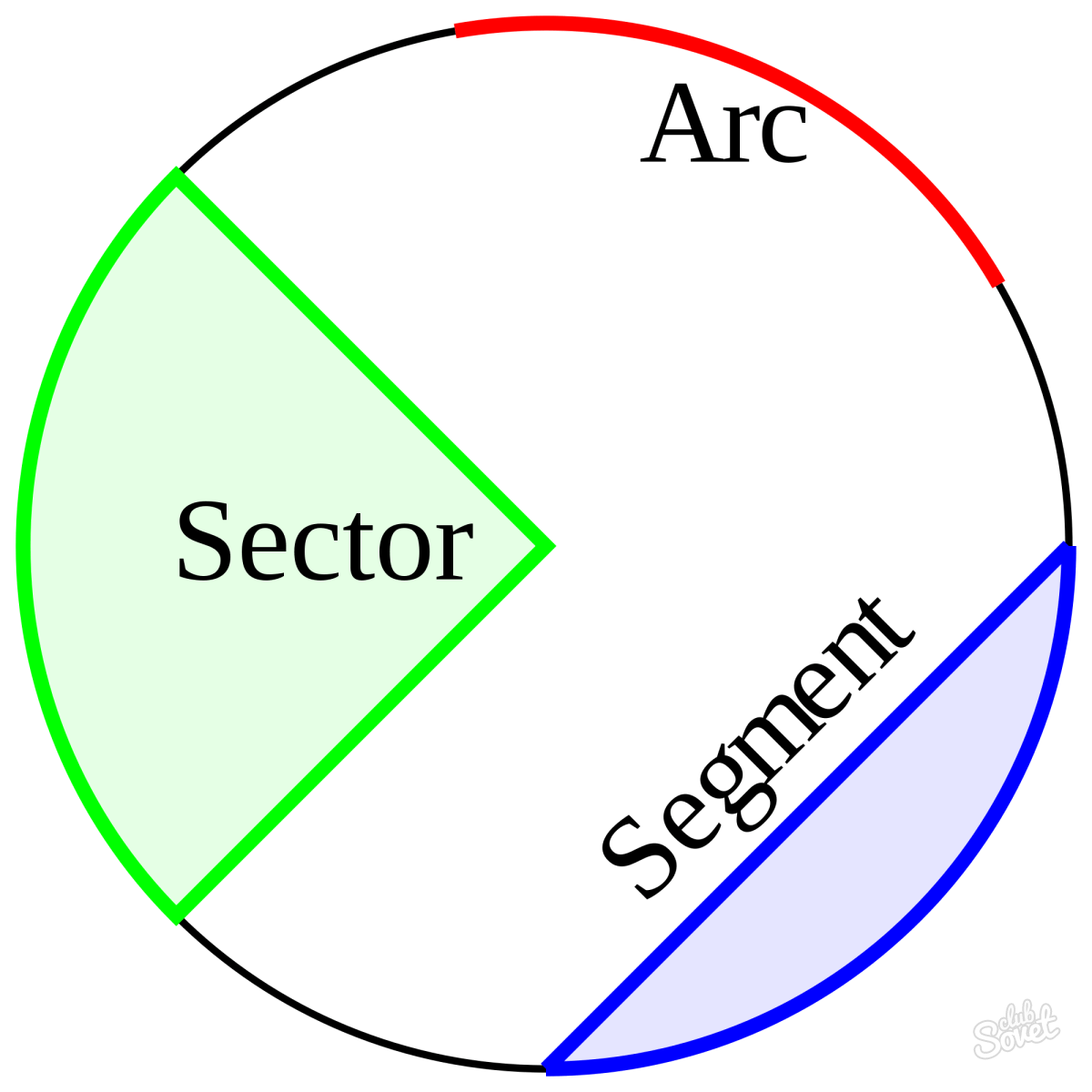
1. Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
   • r – радиус;
   • А – величина угла в градусах.
   • r – радиус;
   • р – длина дуги.

Также существует второй вариант S = 0,5*р*r;

Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А±
S ∆ ;

• r – радиус;
• А – величина угла в градусах;
• S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.

Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн
. Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.

Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.

✍🏻 Часто задаваемые вопросы о площади круга

Площадь круга — один из основных параметров, характеризующих эту геометрическую фигуру. Понимание, как вычислить площадь круга, является важным знанием, которое может применяться в различных сферах жизни — от строительства до математических исследований. В этой статье мы рассмотрим несколько часто задаваемых вопросов о площади круга и предоставим короткие и существенные ответы на них.

Что такое площадь круга?

Площадь круга — это мера плоской фигуры, ограниченной окружностью. Она выражает количество площади, занимаемой этим кругом на плоскости. Площадь круга обычно измеряется в квадратных единицах длины.

Как вычислить площадь круга?

Формула для вычисления площади круга основана на радиусе  — расстоянии от центра круга до окружности.Формула: S = πR², где S — площадь круга, а π (пи) — математическая константа, приближенно равная 3,14159.

Какую роль играет математическая константа π в вычислении площади круга?

Математическая константа π (пи) является ключевой частью формулы площади круга. Она представляет отношение длины окружности к ее диаметру. Значение π является иррациональным числом и приближенно равно 3,14159. Использование π в формуле позволяет точно вычислить площадь круга.

Можно ли упростить вычисление площади круга?

Да, существуют различные аппроксимации и приближенные методы вычисления площади круга. Например, одним из них является метод Монте-Карло, который основан на генерации случайных чисел и оценке вероятностей. Однако, для большинства практических применений рекомендуется использовать точные формулы.

Где можно применить знания о площади круга в повседневной жизни?

Понимание площади круга может быть полезным во многих сферах жизни. Например, в строительстве, площадь круга может использоваться для расчета потребности в материалах или площади поверхности для покрытия. В научных исследованиях знание площади круга может потребоваться для определения площади деталей или областей интереса.

Какую роль играет площадь круга в математическом анализе?

Площадь круга является одним из ключевых параметров при решении различных задач в математическом анализе. Она используется, например, для вычисления объема трехмерных объектов, таких как цилиндр или шар. Площадь круга также является основой для понятия интеграла — основного инструмента математического анализа.

Таблица с формулами площади круга

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	радиус
2	диаметр
3	длина окружности
4	сторона квадратавписанного в круг
5	сторона квадрата,в который вписан круг
6	стороны треугольника
7	сторона равностороннего треугольника
8	высота равностороннего треугольника
9	боковая сторона и основание равнобедренного треугольника
10	стороны при прямом угле треугольника
11	боковая сторона и основание равнобедренного треугольника
12	боковые стороны равнобедренного треугольника и угол между ними
13	стороны прямоугольного треугольника
14	сторона и угол при основании треугольника
15	сторона равностороннего треугольника
16	сторона и угол при основании трапеции
17	боковые стороны и диагональ трапеции
18	стороны прямоугольника
19	сторона и количество сторон многоугольника
20	сторона шестиугольника

Примеры решения задач

Задача 1

Имеется некая окружность с радиусом 12 см. Необходимо вычислить, чему равна длина этой окружности.

Решение

Зная, что вычислить длину окружности при известном ее радиусе можно по стандартной формуле, подставим в выражение числовые значения и запишем ответ:

\(C = 2 \cdot 3,14 \cdot 12 = 75,36\)

Ответ: 75,36 см.

Задача 2

Диаметр окружности равен 15 см. Нужно определить периметр круга, который ограничен этой окружностью.

Решение

Периметр круга в данном случае соответствует длине окружности. Вычислить искомую величину можно, зная диаметр окружности:

\(C = 3,14 \cdot  15 = 47,1\)

Ответ: 47,1 см.

Задача 3

Окружность обладает длиной, равной 12. Ее центр обозначен буквой О. Угол \(\angle AOB\) составляет \(120^{\circ}\). С помощью точек А и В, которые принадлежат окружности, она делится на пару дуг. Требуется вычислить, во сколько раз длина максимальной из образованных дуг больше по сравнению с длиной меньшей.

Решение

Известно, что отношение длин дуг соответствует отношению их градусных мер. Зная, что О является центральной точкой окружности, определим \(\angle AOB\), как центральный. Дуга по градусной мере меньше по сравнению с полуокружностью. Ее градусная мера соответствует градусной мере центрального угла, опирающегося на эту дугу. Меньшая дуга равна \(120^{\circ}\), а градусная мера максимальной дуги составляет \(240^{\circ}\). Таким образом:

\(240 \div 120 = 2\)

Ответ: 2.

Задача 4

На рисунке изображена окружность с центральной точкой О. Длина этой окружности составляет 18 см. Сектор АОВ обладает площадью \(\dfrac{18}{\pi}см^2\). Требуется определить, чему равна длина дуги АВ рассматриваемого сектора.

Решение

Запишем формулу для вычисления длины окружности при ее известном радиусе:

\(С = 2\pi R\)

Согласно условию задачи:

\(18 = 2\pi R\)

В таком случае:

\(R = \dfrac{9}{\pi}\)

Площадь сектора, градусная мера дуги которого составляет \(\alpha\), равна:

\(\pi R^2 \cdot \dfrac{\alpha}{360}\)

Тогда запишем выражение для расчета длины дуги с градусной мерой \(\alpha\):

\(2\pi R\cdot \dfrac{\alpha}{360}\)

Если умножить площадь сектора с дугой, равной \(\alpha\), на \(\dfrac{2}{R}\), то получится определить длину дуги с градусной мерой \(\alpha\). В результате длина дуги АВ рассматриваемого сектора составляет:

\(\dfrac{18}{\pi} \cdot \dfrac{2\pi}{9} = 4\)

Ответ: 4 см.

Задача 5

На рисунке изображено пересечение пары окружностей. Требуется вычислить длину внешней границы фигуры, которая получилась в результате. Длина окружности составляет 12.

Решение

Проведем отрезок через центральные точки окружностей. Соединим центры этих фигур с точками, в которых окружности взаимно пересекаются. Заметим, что можно сформировать пару равносторонних треугольников со сторонами, равными радиусам рассматриваемых окружностей.

Дуга, принадлежащая одной окружности, которая находится внутри сформированной фигуры, имеет опору в виде угла. Этот угол равен паре углов, принадлежащих равностороннему треугольнику, и составляет \(120^\circ\). Таким образом, длину этой дуги допустимо вычислить по следующей формуле:

\(\frac{C_{120^\circ}}{12} = \frac{120^\circ}{360^\circ} \Rightarrow C_{120^\circ} = 4\)

В результате длина внешней границы при пересечении окружностей составляет:

\(L = 2\cdot C — 2\cdot C_{120^\circ} = 2\cdot12 — 2\cdot 4 = 16\)

Ответ: 16.

Задача 6

На рисунке изображена окружность с некоторыми известными величинами. Требуется рассчитать меру \(\angle AOB\).

Решение

Запишем, чему равна общая длина окружности:

С = 1 + 2 + 5 + 10 = 18

В таком случае упрощается нахождение искомого угла:

\(\frac{C_{\angle AOB}}{C} = \frac{\angle AOB}{360^\circ} \Rightarrow \frac{5}{18} = \frac{\angle AOB}{360^\circ} \Rightarrow \angle AOB = 100^\circ\)

Нахождение площади круга — Криста Кинг Математика

Определение площади круга

В этом уроке мы рассмотрим, как использовать формулу площади для круга.

Радиус окружности

Радиус окружности — это длина от центра окружности до точки на ее окружности. Это круг с радиусом ???r???.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Диаметр окружности

Диаметр окружности – это особая хорда, проходящая через центр окружности.

???d=2r???

???r=\frac{1}{2}d???

Это круг диаметром ???d???.

Пи

Пи — это специальное число, которое описывает соотношение между длиной окружности круга и длиной его диаметра. Это примерно равно ???3.14???, что мы записываем как ???\pi \приблизительно 3.14???. 92???. Начнем с работы на примере.

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.

Учить больше

Расчет площади по диаметру

Пример

Какова площадь круга? Округлите ответ до сотых. 9{2}}}???

???r=\sqrt{75}\text{см}???

???r=\sqrt{25}\cdot \sqrt{3}\text{см}???

???r=5\sqrt{3}\text{см}???

Иногда вам нужно найти площадь составной фигуры, состоящей из кругов.

Площадь кольца и других сложных фигур

Если какая-либо фигура образована с помощью нескольких окружностей, то найти ее площадь можно, представив ее в виде суммы площадей нескольких более простых фигур. В качестве простейшего примера можно привести кольцо. По сути оно представляет собой круг, в котором есть круговое отверстие:

Если обозначить наружный радиус кольца буквой R, а радиус отверстия буквой r, то площадь кольца можно найти, вычтя из площади большего круга площадь отверстия:

Задание. Внешний радиус кольца составляет 20 см, а радиус отверстия в нем равен 15 см. Определите площадь кольца.

Решение. Подставляем числа в формулу:

Ответ: 175π.

Задание. Есть диск радиусом 1 метр. Необходимо вырезать в нем отверстие так, чтобы масса диска уменьшилась в два раза. Какой радиус должен быть у отверстия?

Решение. Можно считать, что масса диска пропорциональна его площади, поэтому нам надо, чтобы площадь диска уменьшилась вдвое. Начальная площадь диска определяется так:

Площадь кольца должна быть вдвое меньше, то есть она будет составлять π/2. Если радиус отверстия мы обозначим как r, то можно составить уравнение:

Ответ: ≈ 70,7 см.

В прямоугольной плите с габаритами 180 и 60 см сделано 27 отверстий диаметром 10 см. Вычислите площадь этой плиты. Считайте, что π ≈ 3,1416, и округлите ответ до целых.

Решение. Надо найти площадь плиты без учета отверстий, а потом вычесть из нее площадь всех отверстий. Площадь плиты равна произведению ее сторон

Ответ: ≈ 8679 см2.

Задание. Из вершин квадрата со стороной а проведены дуги радиусом а/2. В результате получили следующую фигуру:

Найдите заштрихованную площадь.

Решение. Площадь заштрихованной области может быть получена, если из площади квадрата мы вычтем площади 4 секторов. Площадь квадрата рассчитывается так:

Задание. В квадрате, сторона которого обозначается буквой а, из вершин провели дуги, чей радиус совпадает со стороной квадрата. В результате в центре квадрата получили следующую фигуру:

Определите, какую долю квадрата занимает эта центральная фигура. Ответ дайте в процентах и округлите его до десятых.

Решение. Задача решается в несколько действий, причем нам потребуется составить формулы для вычисления площадей вспомогательных фигур. Сначала найдем площадь маленького треугольника с «кривыми» сторонами, для чего используем такое построение:

Площадь, которую мы пытаемся найти, обозначена здесь как S₁. Ее можно получить, просто вычтя из площади квадрата (она составляет а2) площади двух секторов и площадь треугольника. Треугольник на рисунке – равносторонний, ведь и сторона квадрата, и радиусы окружностей равны величине а. Тогда каждый его угол составляет 60°, и его площадь можно найти так:

Также мы можем найти центральные углы обоих секторов. Так как углы в квадраты составляют 90°, а в равностороннем треугольнике 60°, то эти углы окажутся равными 90° – 60° = 30°. Тогда площадь сектора вычисляется по формуле:

На следующем шаге вычислим площадь другой фигуры:

Попытаемся выразить величину S₂. Для этого из площади квадрата надо вычесть площадь сектора, у которого центральный угол составляет 90°. Найдем площадь этого сектора:

Здесь мы ищем площадь S3

Обратите внимание, что ее можно выразить через уже найденные нами величины S1 и S2:

Мы составили выражения для всех необходимых нам вспомогательных фигур. Теперь вернемся к исходному рисунке и отметим на нем эти вспомогательные фигуры:

Итак, мы составили выражение для вычисления площади центральной фигуры. По условию надо указать, сколько процентов она составляет от площади всего квадрата. Для ответа на этот вопрос поделим площадь фигуры на площадь квадрата и умножив это отношение на 100%:

Ответ: 31,5%.

В рамках этого урока мы узнали, как вычислять длину окружности и дуги, площади круга, сектора, сегмента, кольца и других фигур, одна или несколько сторон которых представляют собой дуги окружности. Эти навыки могут пригодиться и в реальной жизни, так как именно от площади многих предметов часто зависит потребность в краске, лаке, клее и т. п.

Как рассчитать площадь круга

К примеру, у нас имеется круг с радиусом четыре сантиметра. Давайте рассчитаем его площадь: S={3,14}*4^2={3,14}*16=50,24. Таким образом, площадь окружности составляет 50,24 квадратных сантиметра.

Также, существует специальная формула для расчёта площади круга через диаметр: S={pi/4} d^2.

Давайте рассмотрим пример такого расчёта круга через его диаметр, зная радиус фигуры. Например, мы имеем круг с радиусом равным четырём сантиметрам. Сначала необходимо найти диаметр, который в два раза больше самого радиуса: d=2R, d=2*4=8.

Теперь следует использовать полученные данные для расчёта площади круга по вышеописанной формуле: S={{3,14}/4 }*8^2=0,785*64=50,24.

Как видите, в итоге мы получаем тот же ответ, что и в первом случае.

Знание описанных выше стандартных формул для правильного расчёта площади круга помогут Вам с лёгкостью находить недостающие величины и определять площадь секторов.

Итак, нам известно, что формула для расчёта площади окружности рассчитывается при помощи умножения неизменной величины Пи на квадрат радиуса самой окружности. Сам же радиус можно выразить через фактическую длину окружности, подставив в формулу выражение через длину окружности. То есть: R=l/2pi.

Теперь необходимо подставить в формулу расчёта площади круга данное равенство и в итоге мы получаем формулу нахождения площади этой геометрической фигуры через длину окружности: S=pi{(l/2pi)}^2=l^2/{4pi}.

К примеру, нам дан круг, длина окружности которого составляет восемь сантиметров. Подставляем значение в рассмотренную формулу: S={8^2}/{4*3,14}=64/{12,56}=5. И получаем площадь круга равную пяти квадратным сантиметрам.

Инструкция

Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).

Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».

Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.

• Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
  
• Eratosthenes» Calculation of Earth»s Circumference
  
• Eratosthenes
  

• Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
• Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности
  к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.

Площадь сектора круга

Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.

Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).

Все, что требуется в таких заданиях — это найти радиус окружности R
. Затем можно вычислить площадь круга по формуле S
= πR
2 . Из этой формулы также следует, что для решения достаточно найти R
2 .

Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:

Выполним дополнительные построения в каждой окружности:

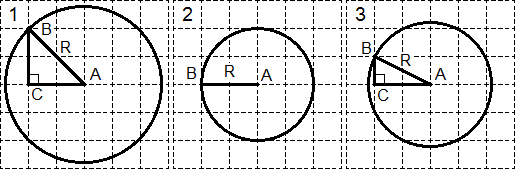
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:

Рассмотрим треугольник ABC
в первой окружности. По теореме Пифагора: R
2 = AB
2 = AC
2 + BC
2 = 2 2 + 2 2 = 8.

Для второй окружности все очевидно: R
= AB
= 2.

Третий случай аналогичен первому. Из треугольника ABC
по теореме Пифагора: R
2 = AB
2 = AC
2 + BC
2 = 1 2 + 2 2 = 5.

Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.

Очевидно, сектор составляет одну четверть круга. Следовательно, S
= 0,25 · S
круга.

Остается найти S
круга — площадь круга. Для этого выполним дополнительное построение:

Треугольник ABC
— прямоугольный. По теореме Пифагора имеем: R
2 = AB
2 = AC
2 + BC
2 = 2 2 + 2 2 = 8.

Теперь находим площади круга и сектора: S
круга = πR
2 = 8π
; S
= 0,25 · S
круга = 2π
.

Наконец, искомая величина равна S
/π
= 2.

Как находить площадь круга

Большое количество точек расположенных на равном расстоянии от центра и находящиеся на одном расстоянии — образуют круг, плоскую фигуру.

Радиус круга — это прямая которая соединяет середину круга с любой из точек находящейся в его окружности. При этом в одной окружности, какая бы точка не была, радиус будет одинаков.

Диаметр круга — это отрезок исходящий от любой точки окружности, проходящий через середину круга и заканчивающийся в параллельной точке той же окружности.

Как находить площадь круга? Площадь круга находится с помощью формулы в которой участвует число ?.

Интересный факт: Числом ? представляется отношение между длиной окружности и длиной диаметра этой же окружности. При этом имеет постоянную величину. А как нам известно ?= 3,1415926 и стало применяться с 1737 года.

Заметка: Ни как не можете определиться, какую машину выбрать? В автосалоне москва автомобили с пробегом (http://center-carauto.ru/), вы сможете в комфортных условиях подобрать наилучший вариант и при этом сэкономить. Согласитесь, заманчивое предложение!
Как рассчитать площадь круга? Как и говорилось выше благодаря формуле, в которой участвует число ? и радиус, записывается так:

S = ?R2

Разберем для наглядности
Найдем площадь круга с помощью его радиуса который равен 4 см.

• Площадь круга равна:
• S= 3,14 * 42 = 3,14 * 16 = 50,24 кв/см
• Так же площадь круга через диаметр находиться по формуле

Решение
S = (?/4)d2

Разберем для наглядности
Найдем площадь круга с помощью его диагонали. Возьмем радиус равный 4 см.

1. Решение
2. S =(3,14/4) * 82 = 0,785 * 64 = 50,24

1) Вычислим диаметр, который больше радиуса в два раза.
d=2R
d = 2 * 4 =8
2) Подставляем значения в формулу
Если сверить полученный ответ с предыдущим, то они равны.

Когда мы ищем площадь сегмента круга или сектора, очень помогает знание основных формул. С их помощью них можно узнавать не известные значения.
Сегментом — называется ограниченная часть круга, которую ограничивают хорда и дуга данного круга.

Как нам уже известно расчет площади круга вычисляется с использованием числа ? умноженного на радиус в квадрате. Используя длину окружности, мы сможем найти радиус.

R = (l/2)?

Если подставить эту формулу в формулу расчета площади., у нас получится:

S = ? ((l/2)?)2 = l2/4?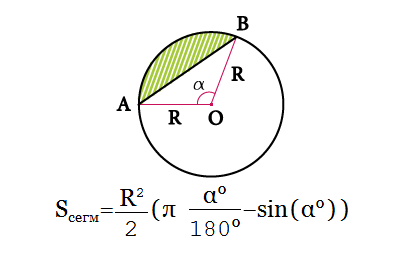

1. Разберем для наглядности
   Найти площадь круга с окружностью равной 8 см.
   Решение
2. Используем формулу S= 82/4*3,14 = 64 / 12,56 = 5 см