Расстояние от точки до точки: формулы, примеры, решения

Выбор системы координат

Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.

Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.

Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.

Я напомню, что в этом разделе мы рассматриваем следующие фигуры:

• куб;
• Прямоугольный параллелепипед;
• Прямая призма (треугольная, шестиугольная…);
• Пирамида (треугольная, четырехугольная);
• Тетраэдр (одно и то же, что и треугольная пирамида).

Уравнения прямой и плоскости

           Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами х и у. Это точки M(x_m; y_m) и N(x_n; y_n)

          Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой y=kx+b подставляли сначала координаты точки М, затем – точки N.

       Получали систему двух линейных уравнений относительно неизвестных коэффициентов k и b, которые находили при решении  этой системы.

        Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0,       (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

        Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (x, y, z).

       Уравнение прямой в пространстве задается через направляющий вектор. Но это уже не входит в рамки программы средней школы, поэтому просто принимаем к сведению.

            Если известны две точки пространства  M( x_m ; y_m ; z_m ) и  N( x_n ; y_n ; z_n ) , то уравнения прямой, проходящей через данные точки, выражаются формулами:

             Но вот что мы с вами можем, так это воспользоваться вектором этой прямой, который будет определяться расстоянием между точками в пространстве. И об этом подробно поговорим в следующем разделе — 

          Привязка фигур к  системе координат позволяет не только определять координаты точек, но и записать уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

  Ax + By + Cz + D = 0

 Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты  А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

       Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

       Прямую можно провести через две точки, и мы составляли два уравнения для двух точек.

         Плоскость можно провести через три точки, значит, и уравнений будет три!

        Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда   вместо D   будет единица, а все остальные коэффициенты будут делиться на D,  назовем их также, А, В, С. И это уже вполне решаемая система!

          Здесь значения всех x, y и z известны, это координаты точек, принадлежащих данной плоскости.

          Итак, точку описать можем, прямую описать можем, плоскость –  можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

Метод координат (продвинутый уровень)

Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:

• Находить координаты вектора;
• Находить длину вектора (альтернативно: расстояние между двумя точками);
• Складывать, вычитать векторы. Умножать их на вещественное число;
• Находить середину отрезка;
• Вычислять скалярное произведение векторов;
• Находить угол между векторами.

Конечно, в эти 6 пунктов не укладывается весь координатный метод.

Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!

Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.

Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую, у которой одна из точек это начало, а соответственно другая конец. Найти расстояние между этими двумя точками, значит найти длину прямой, связывающей точки.

Есть много разных способов найти расстояние между двумя точками, но самый универсальный, на мой взгляд, это найти расстояние взяв за основу Теорему Пифагора. Исходя из этой теоремы, можно сказать, что в нашем случае расстоянием(прямой), является гипотенуза, а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Или же кратко, формулой: \( c^2 = a^2 + b^2 \) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде, где нужно найти расстояние от чего-то до чего-то. Сейчас, мы используя эту теорему найдем расстояние между точками.

Итак, для примера возьмем точки с координатами первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0. Как же нам теперь выразить точки через катеты a и b ? Читайте дальше, все гениальное просто.

На рисунке 1 мы изобразили для наглядности прямоугольный треугольник, с координатами которые мы взяли для примера. На рисунке 2 тот же самый прямоугольный треугольник, только без координат! Эти два прямоугольных треугольника идентичные, поэтому вернемся к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора, на разность координат точек. ​Взгляните на формулу, которая получилась:

Подставляем наши координаты:

В итоге получилось, что расстояние в нашем примере равно 5(корень из 25). Как видите все просто, и вы можете смело применять эту формулу, решая не только задачи, но и на практике, находя расстояние зная только две точки.

Примеры вычисления расстояния между точками в пространстве

Для вычисления расстояния между двумя точками в трехмерном пространстве используется формула:

d = √((x2 — x1)² + (y2 — y1)² + (z2 — z1)²)

В этой формуле x1, y1 и z1 — это координаты первой точки, а x2, y2 и z2 — координаты второй точки. Например, для точек A(1, 2, 3) и B(4, 5, 6) расстояние между ними будет:

d = √((4-1)² + (5-2)² + (6-3)²) = √(27) ≈ 5.2

Примеры расчета Точка A Точка B Расстояние между точками

(1, 2, 3) (4, 5, 6) 5.2 (0, 0, 0) (0, 5, 0) 5 (0, 0, 0) (0, 0, 5) 5

Кроме того, если точки заданы в векторной форме, расстояние между ними можно найти как длину разности векторов:

d = ||B — A|| = √((x2 — x1)² + (y2 — y1)² + (z2 — z1)²)

Чему равно расстояние между векторами B(3, 4, 5) и A(-1, -2, -3)?

Определитель третьего порядка

Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.

Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.

Давай вначале запишем определитель третьего порядка в более общем виде:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right|\),Где \( {{a}_{ij}}\) – некоторые числа.

Причем под первым индеком \( \displaystyle i\) мы понимаем номер строки, а под индеком \( \displaystyle j\) – номер столбца.

Например, \( {{a}_{23}}\) означает, что данное число стоит на пересечении второй строки и третьего столбца.

Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?

То есть, какое конкретно число мы будем ему сопоставлять?

Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:

Как его читать? А понимать его надо следующим образом: мы составляем два выражения:

• Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
• Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
• Тогда определитель равен разности значений, полученных на шаге \( \displaystyle 1\) и \( \displaystyle 2\).

Если записать все это цифрами, то мы получим следующее выражение:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right| = \)\( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — \left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} \right)\)Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

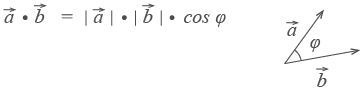
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

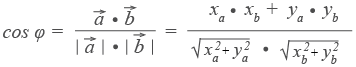
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике , знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.

Вопрос-ответ:

Как определить расстояние между точкой и прямой?

Расстояние между точкой и прямой вычисляется по формуле: d = |ax0 + by0 + c| / sqrt(a^2 + b^2), где x0 и y0 — координаты точки, a, b и c — коэффициенты уравнения прямой ax + by + c = 0. Знак модуля указывает на направление расстояния.

Как найти расстояние между двумя параллельными прямыми?

Расстояние между двумя параллельными прямыми равно расстоянию между любой точкой одной прямой и другой прямой. Для этого можно использовать формулу для нахождения расстояния от точки до прямой. Если уравнения двух параллельных прямых имеют вид ax + by + c1 = 0 и ax + by + c2 = 0, тогда расстояние между ними равно d = |c2 — c1| / sqrt(a^2 + b^2).

Как определить расстояние между двумя не параллельными прямыми?

Расстояние между двумя не параллельными прямыми можно определить по формуле для перпендикулярного расстояния. Для этого нужно найти прямую, перпендикулярную данным прямым и проходящую через пересечение двух данных прямых. Затем можно определить расстояния от этой точки до каждой из данных прямых. Расстояние между прямыми будет равно расстоянию между этой точкой и одной из данных прямых.

Как определить расстояние между двумя точками в трехмерном пространстве?

Формула для определения расстояния между точками в трехмерном пространстве выглядит так: d = sqrt((x2 — x1)^2 + (y2 — y1)^2 + (z2 — z1)^2). Здесь мы просто добавляем квадрат разности координат по оси z.

Как определить расстояние от точки до плоскости в трехмерном пространстве?

Расстояние от точки до плоскости в трехмерном пространстве вычисляется по формуле: d = |ax0 + by0 + cz0 + d| / sqrt(a^2 + b^2 + c^2), где x0, y0 и z0 — координаты точки, a, b, c и d — коэффициенты уравнения плоскости ax + by + cz + d = 0. Знак модуля указывает на направление расстояния.

Какие еще есть способы вычисления расстояний в математике?

Кроме уже перечисленных, существует множество других способов вычисления расстояний в математике. Например, можно вычислить расстояние между окружностью и точкой, кубом и точкой или между двумя произвольными объектами. Также в математике есть такое понятие, как метрика, которая определяет расстояние между объектами в различных пространствах.

1.2 Расстояние между двумя точками; Круги

Учитывая две точки $(x_1,y_1)$ и $(x_2,y_2)$, напомним, что их
горизонтальное расстояние друг от друга равно $\Delta x=x_2-x_1$ и их
вертикальное расстояние друг от друга равно $\Delta y=y_2-y_1$. (Фактически,
слово «расстояние» обычно означает «положительное расстояние». $\Дельта
x$ и $\Delta y$ равны 92=16$.
Теперь мы видим, что это круг с радиусом 4 и центром $(1,-2)$,
который легко изобразить на графике.
$\квадрат$

Пример 1.2.1 Найдите уравнение окружности радиуса 3 с центром:

а) (0,0)$

г) (0,3)$

б) (5,6)$

,-3 $(0,6)$

,-3 $ )$

в) $(-5,-6)$

f) $(3,0)$

(отвечать)

Пример 1.2.2 Для каждой пары точек $A(x_1,y_1)$ и $B(x_2,y_2)$ найти (i) $\Delta x$
и $\Delta y$ при переходе от $A$ к $B$, (ii) наклон линии, соединяющей
$A$ и $B$, (iii) уравнение линии, соединяющей $A$ и $B$, в виде
$y=mx+b$, (iv) расстояние от $A$ до $B$, и (v) уравнение
окружность с центром в $A$, проходящая через $B$.

Отрезки и прямые, связанные с окружностью

Фигура	Рисунок	Определение и свойства
Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды	Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности	Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Фигура	Рисунок	Теорема
Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

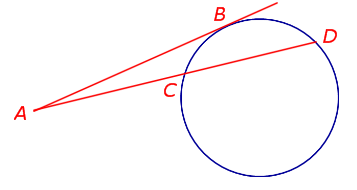
Нахождение длины вектора

Формула нахождения длины вектора \(\vec a\)  зависит от его расположения. Если он находится в плоскости, то есть \(\vec a=\left(a_x;a_y\right)\), то для вычисления потребуется формула:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

\(\left|\vec q\right|=\sqrt{a_x^2+a_y^2}\)

Пример

Узнать длину вектора \(\vec a\) по его координатам (5; -3).

Исходные данные \(a_x=5,\) \(a_y=-3\) подставляем в формулу и вычисляем.

\(\left|\vec a\right|=\sqrt{a_x^2+a_y^2}=\sqrt{5^2+\left(-3\right)^2}=\sqrt{25+9}=\sqrt{34}\)

Если же вектор находится в пространственной системе, то есть \(\vec a=\left(a_x;a_y;a_z\right),\) то для вычисления потребуется формула:

\(\left|\vec a\right|=\sqrt{a_x^2+a_y^2+a_z^2}\)

Пример

Узнать длину вектора \(\vec a\) по его координатам (2; 2; 4).

\(a_x=2, a_y=2, a_z=4\)

Подставляем данные координат из условия и вычисляем:

\(\left|\vec a\right|=\sqrt{a_x^2+a_y^2+a_z^2}=\sqrt{2^2+2^2+4^2}=\sqrt{4+4+16}=\sqrt{24}=2\sqrt6\)

Нахождение длины вектора по координатам.

Длину вектора  будем обозначать . Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор  и он имеет координаты . Получим формулу, позволяющую находить длину вектора  через координаты  и .

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как  и  соответственно и рассмотрим прямоугольник  с диагональю ОА.

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что  и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора  по его координатам на плоскости имеет вид .

Если вектор  представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты  и  являются координатами вектора  в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

.

Теперь получим формулу для нахождения длины вектора  по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор  и обозначим проекции точки А на координатные оси как  и . Тогда мы можем построить на сторонах  и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае  (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора  в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Пример.

Вычислите длину вектора , где  — орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора  по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Ответ:

.

Длина вектора через координаты точек его начала и конца.

А как найти длину вектора, если даны координаты точек его начала и конца?

В предыдущем пункте мы получили формулы для нахождения длины вектора по его координатам на плоскости и в трехмерном пространстве. Тогда мы можем ими воспользоваться, если найдем координаты вектора по координатам точек его начала и конца.

Таким образом, если на плоскости заданы точки  и , то вектор  имеет координаты  и его длина вычисляется по формуле , а формула для нахождения длины вектора  по координатам точек  и  трехмерного пространства имеет вид .

Рассмотрим решения примеров.

Пример.

Найдите длину вектора , если в прямоугольной декартовой системе координат .

Решение.

Можно сразу применить формулу для нахождения длины вектора по координатам точек начала и конца на плоскости :

Вторым вариантом решения является определение координат вектора через координаты точек и применение формулы :

Ответ:

.

Пример.

Определите, при каких значениях  длина вектора  равна , если .

Решение.

Длина вектора  по координатам точек начала и конца может быть найдена как

Приравняв полученное значение длины вектора к , вычислим искомые :

Ответ:

при .

Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

Пусть известны длины двух векторов ,  и угол между ними (или косинус угла), а требуется найти длину вектора  или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Пример.

Длины векторов  и  равны 3 и 7 соответственно, а угол между ними равен . Вычислите длину вектора .

Решение.

Длина вектора  равна длине стороны ВС в треугольнике АВС. Из условия нам известны длины сторон АВ и АС этого треугольника (они равны длинам соответствующих векторов), а также угол между ними, поэтому нам достаточно данных для применения теоремы косинусов:

Таким образом, .

Ответ:

.

Итак, для нахождения длины вектора по координатам используем формулы или ,
по координатам точек начала и конца вектора — или ,
в некоторых случаях к результату приводит теорема косинусов.