Какие фигуры лежат в основании призмы

Площадь и объем фигуры

Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

ПРИЗМА

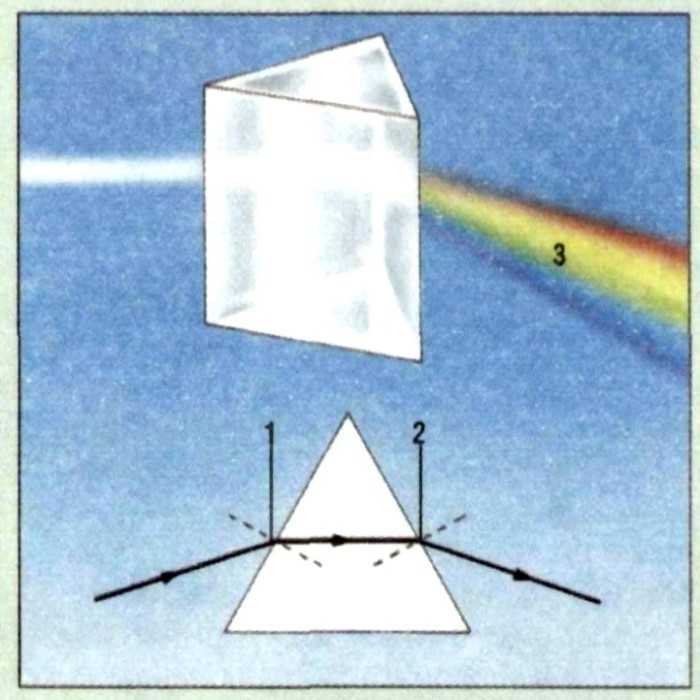
Смотреть что такое «ПРИЗМА» в других словарях:

ПРИЗМА — (греч. prisma, от prio пилю). Стереометрическое тело; тело на двух равных и параллельных основаниях, соединенных параллелограммами; бывают треугольные и четырехугольные. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н.,… … Словарь иностранных слов русского языка

Призма — Призма: Призма геометрическая фигура. Призма устройство для преломления световых лучей, имеющая форму геометрической призмы. Объективная призма (гризма) такая комбинация оптической призмы и дифракционной решётки, которая… … Википедия

ПРИЗМА — ПРИЗМА, призмы, мн. призм, жен. (греч. prisma, букв. нечто распиленное). 1. Многогранник с двумя равными параллельными гранями многоугольниками, т.н. основаниями, и боковыми гранями параллелограммами (мат.). Прямая призма (в которой ребра… … Толковый словарь Ушакова

призма — николь, многогранник, параллелепипед, призмочка Словарь русских синонимов. призма сущ., кол во синонимов: 7 • бипризма (2) • … Словарь синонимов

ПРИЗМА — (греч. prisma букв. отпиленное), многогранник, две грани которого (основания) равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) параллелограммы. По числу боковых граней призмы разделяются на трехгранные,… … Большой Энциклопедический словарь

ПРИЗМА — ПРИЗМА, ы, жен. 1. Многогранник с двумя равными параллельными основаниями многоугольниками и боковыми гранями параллелограммами. 2. Часть оптического прибора предмет такой формы из прозрачного материала. • Сквозь призму чего (смотреть, оценивать) … Толковый словарь Ожегова

ПРИЗМА — греч., геом. долгогранник, тело, из трех и более параллелограмов, с двумя равными и параллельными основаниями; ограненная с боков стопка; | физ. стекляный трегранник, преломляющий свет и разлагающий его на цвета. Призмовый, прзматичный, ческий,… … Толковый словарь Даля

призма — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN prism … Справочник технического переводчика

призма — 2.5.33 призма: Элемент специальной формы (изготовляемый, как правило, из пластмассы), который предназначен для ввода ультразвуковой волны под определенным углом к объекту контроля путем создания акустического контакта между первичным… … Словарь-справочник терминов нормативно-технической документации

Разновидности призм

Все призмы можно разделить на три категории:

Прямая призма – это такая геометрическая фигура, у которой боковые грани соединены с основаниями под прямым углом. Следовательно, они прямоугольники. А саму призму часто еще называют прямоугольным параллелепипедом.
Правильная призма — это геометрическая фигура, в основе которой лежат правильные многоугольники. То есть такие, у которых все стороны равны между собой. И боковые грани таких призм также идентичны друг другу.
Наклонные призмы – это геометрические фигуры, у которых боковые ребра не пересекают основание под прямым углом. Именно в таких призмах появляется такой элемент, как высота.

Диагонали призмы

Следуя таким свойствам, как объем и площадь поверхности, в задачах по геометрии часто встречается информация о длине той или иной диагонали рассматриваемой фигуры, которая либо задана, либо должна быть найдена из других известных параметров. Рассмотрим, каковы диагонали призмы.

Все диагонали можно разделить на два типа:

Расположены в плоскости лица. Они соединяют несмежные вершины либо многоугольника в основании призмы, либо параллелограмма боковой поверхности. Величина длин таких диагоналей определяется на основе знания длин соответствующих ребер и углов между ними. Для определения диагоналей параллелограммов всегда используются свойства треугольников.
Призмы, находящиеся внутри объема. Эти диагонали соединяют разные вершины двух оснований. Эти диагонали полностью находятся внутри фигуры. Их длину рассчитать несколько сложнее, чем для предыдущего типа. Метод расчета предполагает учет длин ребер и основания, а также параллелограммов. Для прямых и правильных призм расчет относительно прост, так как выполняется с использованием теоремы Пифагора и свойств тригонометрических функций.

Затем мы приводим примеры вычисления различных диагоналей.

Диагонали сторон четырехугольной прямой призмы

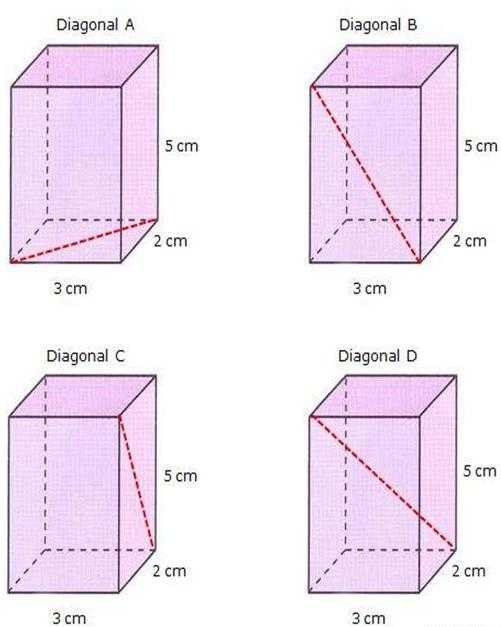
На рисунке выше показаны четыре одинаковые прямые призмы, и даны параметры их ребер. Диагональные призмы A, Diagonal B и Diagonal C показывают диагонали трех разных граней пунктирной красной линией. Так как призма представляет собой прямую с высотой 5 см, а основание представляет собой прямоугольник со сторонами 3 см и 2 см, то найти отмеченные диагонали несложно. Для этого нужно воспользоваться теоремой Пифагора.

Длина диагонали основания призмы (диагональ А) равна:

DA = √(32+22) = √13 ≈ 3,606 см.

Диагональ боковой грани призмы (см. Диагональ B):

DB = √(32+52) = √34 ≈ 5,831 см.

Наконец, длина другой боковой диагонали (см. Диагональ C):

ДС = √(22 + 52) = √29 ≈ 5,385 см.

Длина внутренней диагонали

Теперь вычислим длину диагонали квадратной призмы, которая изображена на предыдущем рисунке (Диагональ D). Это не так уж сложно сделать, если вы заметили, что это гипотенуза треугольника, где катеты будут высотой призмы (5 см) и диагональю D, показанной на рисунке вверху слева (диагональ А). Затем мы получаем:

DD = √(DA2+52) = √(2 2+32+52) = √38 ≈ 6,164 см.

Призма

Определения:

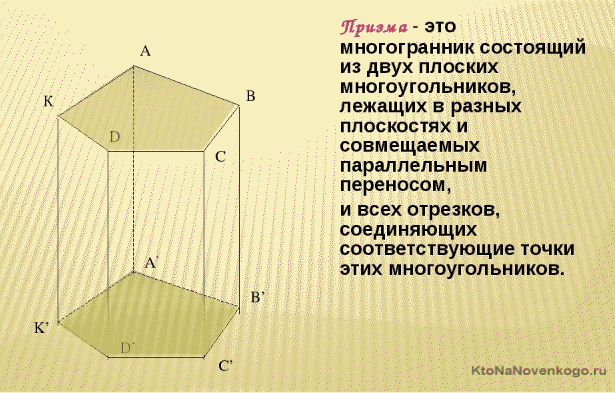
Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
Боковая поверхность – объединение боковых граней.
Полная поверхность – объединение оснований и боковой поверхности.
Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра призмы параллельны и равны.
Объём призмы равен произведению её высоты на площадь основания:

где: S_осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A₂B₂C₂D₂E₂).
Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S_сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA₁или BB₁ и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P_сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P_осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S_осн∙h = S_осн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны между собой.
Правильная призма является прямой.

5 комментариев

Тут всё понятно,впервые начинаю понимать стереометрию

Супер Aper! Рады помочь!

Когда читаю теорию этого учебника, такое ощущение, что я разговариваю с другом. Настолько все просто и приятно. Сказать, что я влюбилась в этот материал, ничего не сказать. Спасибо вам!

Бася, вы нас растрогали таким комментарием. Спасибо большое! Удачи на экзамене!

Некоторые комментарии прошлых лет об этой статье:

Илья 26 ноября 2017 Огромное вам спасибо за созданный сайт, он очень удобен и информативен. Мне сложно представить какое количество времени было потрачено на «переработку» материала в понятном и доступном виде.Теперь есть источник чистых знаний, без лишней «воды», который не только помогает узнать новое, но и систематизировать информацию в голове. Жаль, что я не нашел сайт раньше. Вы лучшие!

Дмитрий 21 февраля 2018 Сайт отличный!Все подробно описано. Никогда не понимал эту тему, но благодаря создателям этого сайта я наконец понял эту тему. Спасибо вам за ваши труды. Очень вам благодарен.

Regina 29 марта 2018 Аааааааа,это просто лучшее. Никогда не разбиралась в геометрии…Готовясь к зачету искала все сайты на эту тему. Нашла вас. Ввы все объяснили просто и доступно. Спасибо большое!

Настя 21 мая 2018 Красивый сайт, ничего глаза не режет, смотреть и читать приятно.

Женя 27 февраля 2019 можете указать свои инициалы? мне это для проекта надо)

Анна 29 апреля 2019 Преподнесено очень понятным языком, с наглядными картинками, спасибо) Хотелось бы хоть пример одной задачи и решение чтобы было открыто бесплатно, чтобы понять на сколько хорошо поясняете, но я думаю все ок.

Николай 04 июня 2020 Все очень доступно и понятно. Только вот не написано в статье про диагональ призмы. А так все просто супер, подготовился к сессии по данному материалу

Алексей Шевчук 05 июня 2020 Николай, спасибо. Диагонали в разных призмах разные, а в треугольной её и вовсе нет, поэтому длина диагонали — частный случай, а не какая-то полезная формула. Стоит рассмотрения разве что диагональ прямоугольного параллелепипеда — она вычисляется по теореме Пифагора и равна корню из суммы квадратов рёбер.

Элементы

Перед тем, как приступить к разбору и решению геометрических задач, следует разобраться с терминологией. Введем понятия для всех основных компонентов призмы. Сделать это целесообразно, используя рисунок, представленный ниже:

Перечислим элементы геометрического объекта, сопровождая их соответствующими расшифровками:

Основания имеют форму одинаковых многоугольников. В соответствии с форматом таких фигур определяют тип призмы. На рисунке выше представлен геометрический объект, обладающий основаниями в форме параллелограммов, а именно ABCD и \(A_{1}B_{1}C_{1}D_{1}1\).
Боковые грани в данном примере изображены как параллелограммы и обозначены за \(AA_{1}B_{1}B, BB_{1}C_{1}C, CC_{1}D_{1}D и AA_{1}D_{1}1D\).
Боковое ребро является отрезком, с помощью которого соединены соответствующие друг другу вершины разных оснований \((AA_{1}, BB_{1}, CC_{1} и DD_{1})\). Боковое ребро играет роль единой стороны прилегания пары боковых граней.
Высота h представляет собой перпендикулярный отрезок прямой, обозначающий расстояние между парой оснований. Когда ребра по бокам призмы перпендикулярны рассматриваемым основаниям, считают, что такие ребра приобретают смысл высот геометрической фигуры.
Диагональ основания изображена в виде отрезка, соединяющего пару вершин, расположенных друг напротив друга на едином основании. На изображении диагонали обозначены отрезками \(AC, BD, A_{1}C_{1} и B_{1}D_{1}\). Если речь в задаче идет о треугольной призме, то диагональ отсутствует.
Диагональ боковой грани представляет собой отрезок, соединяющий пару вершин, которые расположены напротив друг друга и принадлежат одной грани. В геометрической фигуре, рассмотренной на графическом изображении, роль данных элементов играют отрезки \(CD_{1} и C_{1}D\).
Диагональ призмы является отрезком, с помощью которого соединены две вершины, принадлежащие неодинаковым основаниям и разным боковым граням. В качестве примера таких компонентов геометрического объекта можно привести фрагменты прямых \(AC_{1} и B_{1}D\).
Поверхность призмы является суммой поверхности пары оснований рассматриваемой фигуры и ее граней, расположенных по бокам.

Сечения призмы

Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.

Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.

Сечения конуса

Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:

круглое;
эллиптическое;
параболическое;
гиперболическое;
треугольное.

Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.

Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:

S1 = pi*r2*z2/h2

Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.

Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:

S2 = r*h

Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.

Совет 4: Как обнаружить площадь сечения куба

Вопрос относится к аналитической геометрии. Он решается с привлечением уравнений пространственных прямых и плоскостей, представления куба и его геометрических свойств, а также с применением векторной алгебры. Могут потребоваться методы рения систем линейных уравнений.

Инструкция

1. Выберите данные задачи так, дабы они были исчерпывающими, но не избыточными. Секущую плоскость ? следует задать всеобщим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба абсолютно хватит координат всяких 3 его вершин. Возьмите, скажем, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.

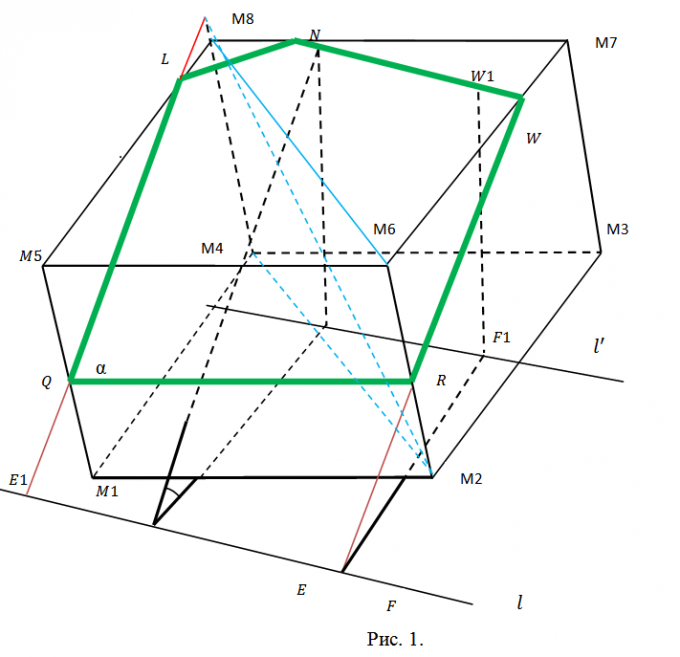
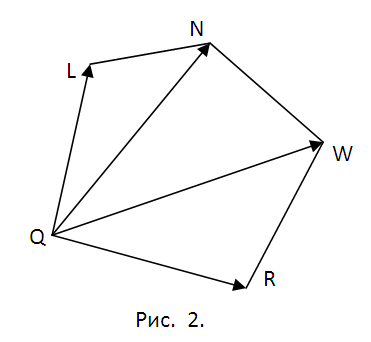
2. Определитесь с планом последующей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью ?. Позже этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади всякого из них с поддержкой свойств векторного произведения. Методология всякий раз одна и та же. Следственно дозволено ограничиться точками Q и L и площадью треугольника ?QLN.

3. Направляющий вектор h прямой, содержащий ребро М1М5 (и точку Q), обнаружьте как векторное произведение M1M2={x2-x1, y2-y1, z2-z1} и M2M3={x3-x2, y3-y2, z3-z2}, h={m1, n1, p1}=. Полученный вектор является направляющим и для всех прочих боковых ребер. Длину ребра куба обнаружьте как, скажем, ?=?( (x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Если модуль вектора h |h|??, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)?. Сейчас запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). Позже подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).

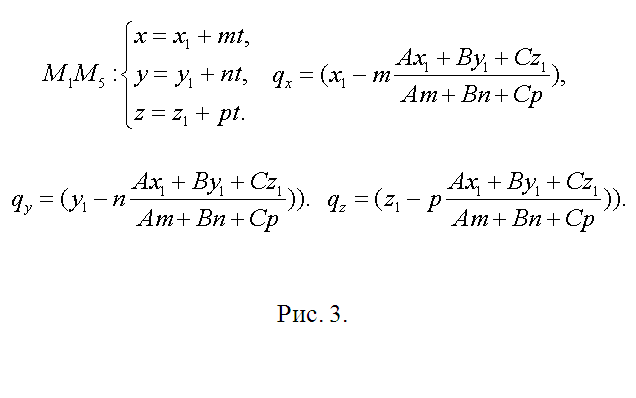
4. Видимо, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. После этого повторите предыдущие рассуждения касательно точки L(lx, ly, lz) (см. рис. 4). Все последующее, для N(nx, ny, nz) – точная копия это шага.

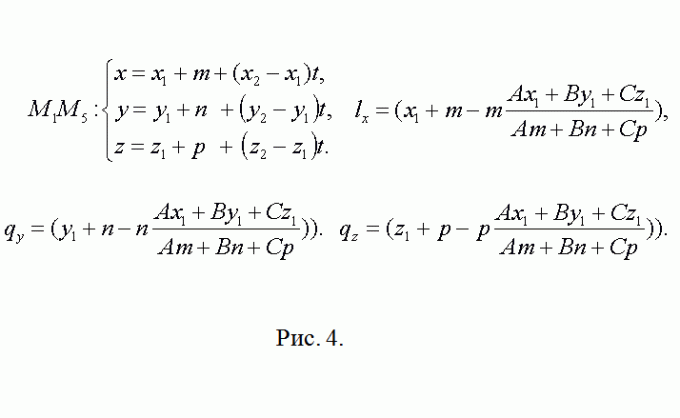
5. Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический толк их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Следственно площадь ?QLN S1=(1/2)||. Следуйте предложенной методике и вычислите площади треугольников ?QNW и ?QWR – S1 и S2. Векторное произведение комфортнее каждого находить с поддержкой вектора-определителя (см. рис. 5). Запишите окончательный результат S=S1+S2+S3.

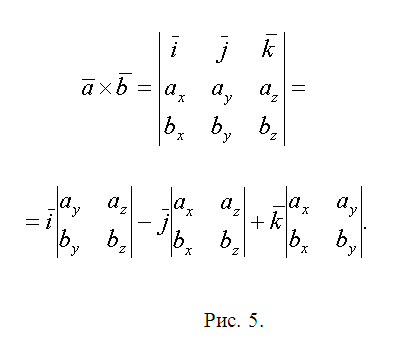
Что такое призма — определение и разновидности призм

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем о такой интересной геометрической фигуре, как ПРИЗМА.

Школьники сталкиваются с ней на уроках геометрии только в 10 классе. Соответственно, те, кто решил уйти после 9-го класса в колледж, этих знаний лишены. И мы восполним этот пробел.

А старшеклассникам наша статья (очень на это надеемся) поможет при подготовке к сдаче ЕГЭ. На экзаменах по математике попадаются несколько вопросов, связанных с ПРИЗМАМИ.

Призма – это геометрическая фигура, которая представляет собой объемный многогранник. Две его стороны лежат на параллельных основаниях и представляют собой различные многоугольники. А боковые грани – это параллелограммы, которые соединяются с основаниями.

Выглядит классическая призма так, как показано на рисунке выше.

На этом рисунке четко видны все элементы призмы:

В зависимости от вида основания призмы бывают:

Разнообразие призм можно считать бесконечным. Могут быть фигуры, у которых в основании и 10-угольник, и 20-угольник, и даже 100-угольник. Но, к счастью, такие фигуры попадаются крайне редко. И их точно не изучают в школе.

Определение параллелепипеда

Другой тип прямоугольной призмы — параллелепипед.

Параллелепипед — это квадратная призма, все грани которой — параллелограммы.

Параллелепипеды повсюду: ящики, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда.

Свойство параллелепипеда, видимое невооруженным глазом: противоположные стороны параллелепипеда равны. В качестве примера рассмотрим ту же комнату: потолок и пол равны, как и стены напротив друг друга.

Нельзя не упомянуть об очень важном свойстве параллелепипеда:

Все диагонали пересекаются в одной точке и делятся этой точкой пополам. Это свойство относится ко всем типам параллелепипедов.

Что такое параллелепипеды?

Параллелепипеды также могут быть прямыми и наклонными. В этих случаях все определения такие же, как и для всех других призм.

Наклонный параллелепипед: свойства, формулы и задачи репетитора по математике

Параллелепипедом называется четырехугольная призма, в основаниях которой лежат параллелограммы. Высотой параллелепипеда называют расстояние между плоскостями его основаниями. На рисунке высота показана отрезком . Различают два вида параллелепипедов: прямой и наклонный. Как правило, репетитор по математике сначала дает соответствующие определения для призмы, а затем переносит их на параллелепипед. Мы сделаем также.

Напомню, что призма называется прямой, если ее боковые ребра перпендикулярны основаниям, если перпендикулярности нет – призму называют наклонной. Эту терминологию наследует и параллелепипед. Прямой параллелепипед – ни что иное, как разновидность прямой призмы, боковое ребро которой совпадает с высотой. Сохраняются определения таких понятий, как грань, ребро и вершина, являющиеся общими для всего семейства многогранников. Появляются понятие противоположные грани. У параллелепипеда 3 пары противоположных граней, 8 вершин ти 12 ребер.

Свойства наклонного параллелепипеда:

1) Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
3) Каждый параллелепипед состоит из шести равных по объему треугольных пирамид. Чтобы показать их ученику репетитор по математике должен отрезать от параллелепепеда половинку его диагональным сечением и разбить ее отдельно на 3 пирамиды. Их основания должны лежать в разных гранях исходного паралеллепипеда. Репетитор математики найдет применение этого свойства в аналитической геометрии. Оно используется для вывода объема пирамиды через смешанное произведение векторов.

Формулы объема параллелепипеда:
1) , где — площадь основания, h – высота.
2) Объем параллелепипеда равен произведению площади поперечного сечения на боковое ребро .Репетитору по математике: Как известно, формула является общей для всех призм и если репетитор уже доказал ее, нет смысла повторять тоже самое для параллелепипеда. Однако в работе со учеником среднего уровня (слабому формула не пригодиться) преподавателю желательно действовать с точностью до наоборот. Призму оставить в покое, а для параллелепипеда провести аккуратное доказательство.
3) , где –объем одной из шести треугольных пирамиды из которых состоит параллелепипед.
4) Если , то

Площадью боковой поверхности параллелепипеда называется сумма площадей всех его граней:
Полная поверхность параллелепипеда – это сумма площадей всех его граней, то есть площадь + две площади основания: .

О работе репетитора с наклонным параллелепипедом:
Задачами на наклонный параллелепипед репетитор по математике занимается не часто. Вероятность их появления на ЕГЭ достаточно мала, а дидактика неприлично бедная.

Более-менее приличная задача на объем наклонного параллелепипеда вызывает серьезные проблемы, связанные с пределением расположения точки Н — основания его высоты.

В этом случае репетитору по математике можно посоветовать обрезать параллелепипед до одной из шести его пирамид (о которых идет речь в свойстве №3), попробовать найти ее объем и умножить его на 6.

Задачи репетитора по математике:
1) Грани параллелепипеда равные роибы со стороной 2см и острым углом . Найти объем параллелепипеда.
2) В наклонном параллелепипеде боковое ребро равно 5см. Сечение, перпендикулярное ему, является четырехугольником со взаимно перпендикулярными диагоналями, имеющими длины 6см и 8 см. Вычислить объем паралеллепипеда.

3) В наклонном параллелепипеде известно, что , а в онованием ABCD является ромб со стороной 2см и уголом . Определите объем параллелепипеда.

Репетитор по математике, Александр Колпаков

Элементы пирамиды

Для рисунка выше:

Основание (четырехугольник ABCD) – грань фигуры, являющая многогранником. Ей не принадлежит вершина.
Вершина пирамиды (точка E) – общая точка всех боковых граней.
Боковые грани – треугольники, которые сходятся в вершине. В нашем случае это: AEB, AED, BEC и CED.
Боковые ребра – стороны боковых граней, за исключением тех, которые принадлежат основанию. Т.е. это AE, BE, CE и DE.
Высота пирамиды (EF или h) – перпендикуляр, опущенный из вершины пирамиды на ее основание.
Высота боковой грани (EM) – высота треугольника, являющегося боковой гранью фигуры. В правильной пирамиде называются апофемой.
Площадь поверхности пирамиды – площадь основания и всех ее боковых граней. Формулы для нахождения площади поверхности (правильной фигуры), а также объема пирамиды представлены в отдельных публикациях.

Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.

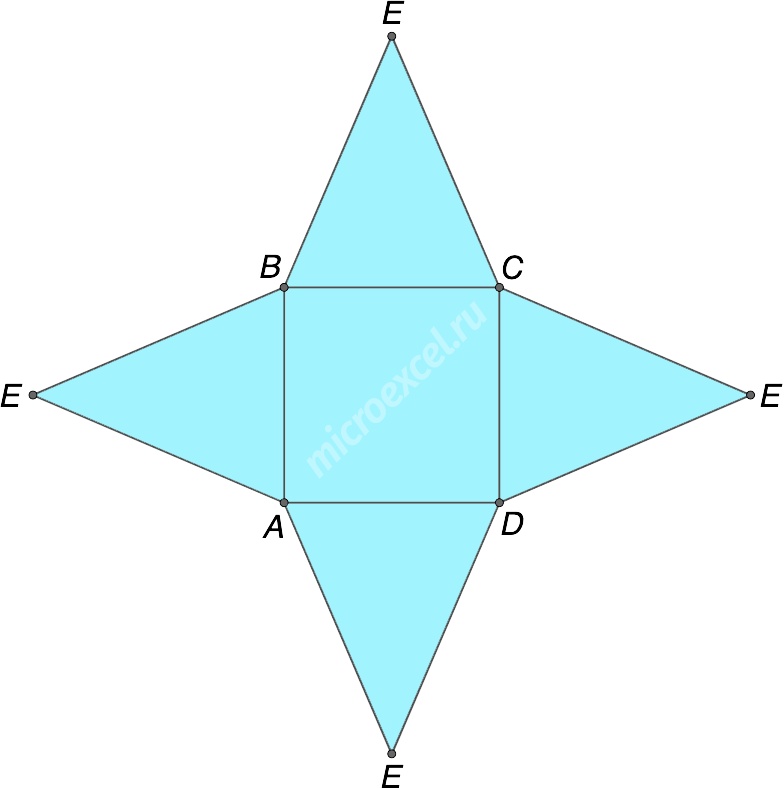
Примечание: свойства пирамиды представлены в отдельной публикации.

Строение призмы

Представьте себе обычную коробку. Основание и крышка подобны и лежат в параллельных плоскостях. Это равные многоугольники. Их еще называют основаниями призмы.

Посмотрим на боковые стороны коробки. Это параллелограммы, только с прямыми углами. Подробнее о параллелограммах можно прочитать в статье «Параллелограмм». Эти параллелограммы называются сторонами призмы.

Возьмите линейку и измерьте расстояние между основаниями призмы. Для этого из любой точки основания проводим перпендикуляр к другой.

Подробнее о расстояниях между плоскостями можно прочитать в статьях «Углы в пространстве» и «Расстояния между фигурами».

Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы.

Высота призмы – это перпендикуляр, проведенный из любой точки одного основания к другому основанию призмы.

В задачах гораздо удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы.

Рассмотрим элементы призмы.

Ребро – это линия пересечения двух плоскостей.

Представим, что вместо картонных стенок в нашей коробке ткань, которую мы должны натянуть на раму, чтобы коробка не менялась. В этом случае все линии в этой рамке будут ребрами.

Ребра бывают двух видов:

нижние края,
боковые ребра.

Их также легко различить: ребра основания являются стороной входящего в него многоугольника, а боковые ребра основаниям не принадлежат.

Боковые ребра имеют очень важную характеристику: они равные и параллельные.

Диагональ призмы — это отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Например, мы можем взять клетку для попугая и сделать из угла в угол насест, чтобы птичке было весело жить. Этот насест будет диагональю призмы.

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.