Как искать объем параллелепипеда?

Решение задач

На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:

1. Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
2. Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
3. Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
4. В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.

Формула расчета в двух вариантах

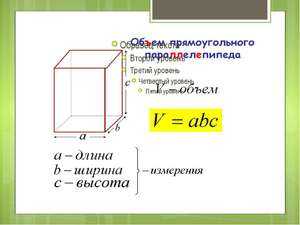
Итак, для расчета по формуле нужно знать длину, ширину и высоту измеряемого предмета. Эти данные следует обозначить соответственно как А, B и C, а объем обычно представляют буквой V. Формула для определения объема прямоугольного параллелепипеда при этом будет выглядеть следующим образом: V = A x B x C.

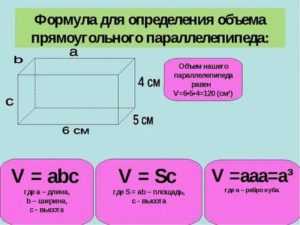
Если определятся объем бассейна, то необходимо его длину, ширину и глубину перемножить. Для более простого восприятия давайте разберем правила расчета объема параллелепипеда на примере. Допустим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.

Можно выделить и другую формулу, которая имеет некоторое отличие. Она представляет собой произведение площади основания на высоту. Формула выглядит следующим образом: V = S x h. Здесь h — высота параллелепипеда. S — площадь основания, которая представлена произведением двух сторон основания. Обычно их обозначают, как a и b: S = a x b.

При расчете можно пользоваться любой из двух приведенных формул. Обе являются верными и позволяют получить точные данные. Последний вариант удобен, когда уже известна площадь основания. Если же она неизвестна, проще перемножать сразу три линейных размера, исключая необходимость в лишней процедуре.

Практическое применение

Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.

Доказательство теорем

Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).

Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.

Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.

Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.

Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.

Решение задач

Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.

Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.

Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.

Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).

Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.

Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.

Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:

• 78 = корень из суммы 5508+с2
• 782 = 5508 + с2
• с2 = 6084 — 5508.
• С2 = 576.

Ответ: объем составляет 576.

Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.

KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².

Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.

В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.

Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.

Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.

В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.

Высота треугольника делит его основание пополам. По теореме Пифагора она равна:

• FK2 + (AC/2)2 = FC2;
• FK2 + 16 = 25;
• FK2 =25−16 = 9;
• FK = 3 см.

Высота фигуры составляет 3 см.

Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.

Площадь параллелепипеда. Формулы и задачи

Формула нахождения полной площади параллелепипеда

Параллелепипед – это четырехугольная призма, в основании имеющая параллелограмм. Существуют готовые формулы для расчета боковой и полной площади поверхности фигуры, для которых необходимы лишь длины трех измерений параллелепипеда.

Как найти площадь боковой поверхности прямоугольного параллелепипеда

Необходимо различать прямоугольный и прямой параллелепипед. Основание прямой фигуры может представлять собой любой параллелограмм. Площадь такой фигуры необходимо вычислять по другим формулам.

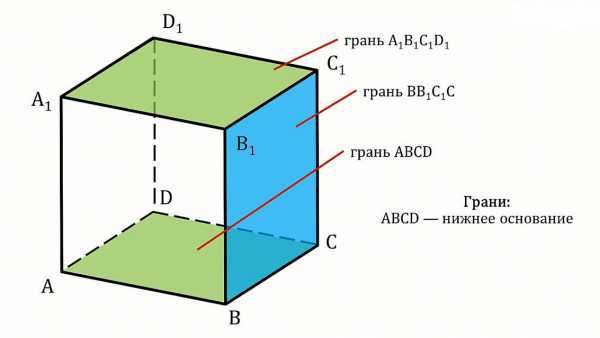
Сумма S боковых граней прямоугольного параллелепипеда вычисляется по простой формуле P*h, где P – периметр и h – высота. На рисунке видно, что у прямоугольного параллелепипеда противоположные грани равны, а высота h совпадает с длиной ребер, перпендикулярных основанию.

Площадь поверхности прямоугольного параллелепипеда

Полная площадь фигуры состоит из боковой и площади 2-х оснований. Как найти площади прямоугольного параллелепипеда:

, где a, b и c – это измерения геометрического тела.Описанные формулы просты для понимания и полезны при решении множества задач геометрии. Пример типового задания представлен на следующем изображении.

При решении подобного рода задач следует помнить, что основание четырехугольной призмы выбирается произвольно. Если за основание принять грань с измерениями x и 3, то значения Sбок будет иным, а Sполн останется 94 см2.

Площадь поверхности куба

Куб – это прямоугольный параллелепипед, у которого все 3 измерения равны между собой. В связи с этим формулы полной и боковой площади куба отличаются от стандартных.

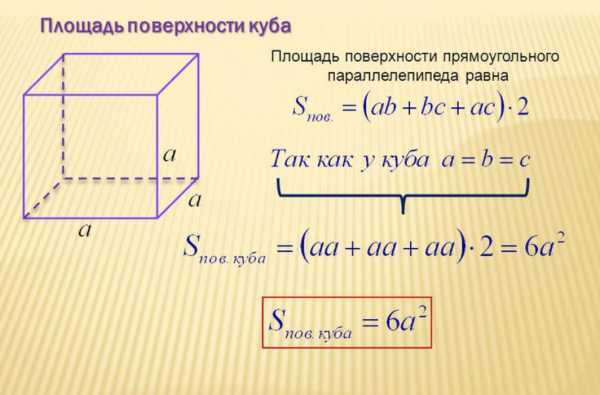
Периметр куба равен 4a, следовательно, Sбок= 4*a*a = 4*a2. Данные выражения не обязательны для заучивания, но значительно ускоряют решение заданий.

Пример решения задачи

Приведенные формулы могут использоваться в ходе поиска диагоналей параллелепипеда.

Для нахождение B1D достаточно применить теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы.

Формулы вычисления объёма прямоугольника и параллелепипеда

Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей.

Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д.

, чего уж говорить о школьниках, которые только-только начинают свой математический путь.

Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.

Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:

1. Линейка, для того чтобы измерить необходимые нам данные.
2. Калькулятор, для того чтобы в дальнейшем подсчитать расчеты.

Вычисление объема прямоугольного параллелепипеда

Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.

Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.

Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.

1. После прочтения задачи, нужно определить что именно следует найти; длину фигуры, объем или же площадь.
2. Какая именно часть фигуры рассматривается в задаче — ребро, вершина, грань, сторона, а может быть, вся фигура целиком?

Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:

V=a*b*h,

V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.

Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах

Пример первый

Определим объем бака для спирта, при следующих размерах:

• длина три метра;
• ширина два метра пятьдесят сантиметров;
• высота триста сантиметров.

Для начала обязательно согласовываем единицы измерения и перемножаем их:

3*2.5*3.

Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.

Пример второй

Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.

Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.

Итак, начнем с сантиметров. Переводим метры в сантиметры:

V = 400 * 70 * 80;

V = 2240000 сантиметров в кубе.

Теперь метры:

V = 4* 0.7 * 0.8;

V = 2.24 метра в кубе.

Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.

Пример третий

Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:

V = a * b * h;

где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5

Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:

V = 5 * 3 * 2.5;

V = 37.5 метра в кубе.

Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.

Применение формул объема и площади поверхности прямоугольного параллелепипеда для решения практических задач и математического моделирования

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (180,7 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию

Цель урока: На практике научиться применять формулы объёма и площади поверхности прямоугольного параллелепипеда.

Инструменты: мультимедийная установка, мел, доска, макеты параллелепипедов.

II. Устный опрос.

1. Сколько ребер у прямоугольного параллелепипеда? Какой фигурой они являются?
2. Сколько граней у прямоугольного параллелепипеда? Какой фигурой они являются?
3. Сколько вершин у прямоугольного параллелепипеда? Какой фигурой они являются?

III. Работа по готовым чертежам.

1. Что такое a, b и c?
2. Как найти площадь боковой грани? Есть ли еще грани с такой же площадью?
3. Как найти площадь верхней грани?
4. Как найти площадь передней грани?
5. Записать на доске формулу для нахождения площади поверхности параллелепипеда.
6. Записать формулу для нахождения объёма параллелепипеда.
7. В каких единицах измеряется площадь поверхности параллелепипеда, а в каких объём.

IV. Решить задачу по чертежу, изображенному на рисунке.

Найти площадь поверхности и объём прямоугольного параллелепипеда.

Решение.

1. 3*4 = 12 (кв. см) – площадь передней поверхности.
2. 3*5 = 15 (кв. см) – площадь боковой поверхности.
3. 4*5 = 20 (кв. см) – площадь верхней поверхности.
4. 2*(12+15+20) = 94 (кв. см) – площадь боковой поверхности параллелепипеда.

Ответ: 94 кв.см.

V. Практическая часть. Раздать параллелепипеды

1. Измерить ребра параллелепипеда (длину, высоту и ширину). Записать результаты в тетрадь.
2. Найти площадь боковой поверхности параллелепипеда.
3. Найти объем параллелепипеда.
4. Подписать грань параллелепипеда площадь, которой равна

• Вариант 1 – 14 кв. см
• Вариант 2 – 18 кв. см
• Вариант 3 – 48 кв. см

VI. Письменная работа на доске с фронтальным обсуждением.

Задача.

Найти площадь поверхности и объём прямоугольного параллелепипеда с вырезом.

Решение.

1. 2*(4*5+5*5+5*4) = 130 кв. см – площадь поверхности.
2. 5*5*4 = 100 куб. см – объём параллелепипеда.

Ответ: 130 кв. см и 100 куб. см.

VII. Задача с практическим содержанием.

Сколько ведер воды по 8 литров каждое, налито в аквариум, изображенный на рисунке.

Мы знаем, что 1 литр = 10 куб.дм.

1. 25-5 = 20 (см) – высота налитой воды.
2. 20*40*60 = 48000 (куб. см) – объём воды в аквариуме.
   48000 куб. см = 48 куб. дм = 48 литров
3. 48:8 = 6 (вед.) – воды потребуется.

Ответ: 6 ведер.

Как найти объем неправильной формы

Неправильная форма может быть любой сложности и не иметь фиксированных размеров. В таких случаях, для нахождения объема, нужно измерить три измерения: длину, ширину и высоту. Таким образом, объем можно найти, умножив значения этих измерений.

Однако, если форма не имеет правильной формы, необходимо использовать другие методы для нахождения объема. Например, можно разделить неправильную форму на несколько простых геометрических фигур, для каждой из которых уже известна формула для нахождения объема. Затем, найденные объемы можно сложить между собой, чтобы получить итоговое значение.

Таким образом, для нахождения объема неправильной формы необходимо использовать знания по геометрии и математике, а также творчески подходить к решению задач.

О чем еще следует знать для правильности расчета?

Для вычисления объема параллелепипеда необходимо понять, что это за фигура. Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:

1. Прямоугольный параллелепипед. Эта фигура представляет собой параллелепипед, который имеет все грани в виде прямоугольников.
2. Прямым параллелепипедом является фигура, у которой 4 боковые грани — прямоугольники.
3. Куб — это еще один вид параллелепипеда. Он представляет собой прямоугольный параллелепипед, все стороны которого равны между собой. Другими словами, все шесть граней такой фигуры, как куб — это равные квадраты.

И также важно помнить о том, что в процессе выполнения расчета у каждой составляющей формулы должна быть одна и та же размерность. Если опустить это простое правило, получить верный результат не удастся

Если вы выполняете расчеты просто на уроках математики, проблемой могут стать только неудовлетворительные оценки. А при проектировании и наличии ошибок в расчетах проблемы могут быть более серьезными.

Не стоит думать, что основные математические формулы по определению объемов геометрических фигур встречаются исключительно на уроках математики. В большинстве случаев они пригодятся и в последующей жизни. В частности, во время ремонтных или строительных работ, при проектировании и декорированию интерьера, а также в ряде других случаев. Именно тогда без правильной формулы обойтись не удастся.

Можно подвести итог: объем параллелепипеда равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при любом вращении и повороте. Результат будет неизменным.

Решение задачи: Объём параллелепипеда V вычисляется по формуле V=abc , где a,b,c — его измерения А)Вычислите неизвестную

В задании, наверняка, речь идёт о прямоугольном параллелепипеде, объём (V) которого вычисляется по формуле V = a * b * c, где a, b, c — его измерения (рёбра).

А) 1. Дано: V = 48 см 3 , b = 3 см, с = 4 см. Найдём длину неизвестного ребра (измерения) а. Имеем: а * (3 см) * (4 см) = 48 см 3 или 12 * а = 48 см, откуда а = (48 см) : 12 = 4 см.

1. Дано: V = 210 см 3 , а = 6 см, с = 7 см. Длина измерения b неизвестна. Найдем ее: (6 см) * b * (7 см) = 210 см 3 или 42 * b = 210 см, откуда а = (210 см) : 42 = 5 см.
2. Дано: V = 24 м 3 , а = 3 м, b = 2 м. Необходимо найти длину ребра с. Имеем: (3 м) * (2 м) * с = 24 м 3 или 6 * с = 24 м, откуда с = (24 м) : 6 = 4 м.

Б) Предположим, что у прямоугольного параллелепипеда, имеющего известный объём V, известны два измерения, например, длина а и ширина b основания (то есть, прямоугольника). Необходимо найти высоту с (третье измерение). Воспользуемся вышеописанной формулой: V = a * b * c. Это равенство рассмотрим как уравнение с одной неизвестной (с) и решим его. Применяя правило нахождения решения линейных уравнений, получим с = V / (a * b).

Ответы: А) 4 см; 5 см; 4 м. Б) с = V / (a * b).

Как найти объем прямоугольного параллелепипеда?

Прямоугольный параллелепипед, с точки зрения математики, является объемной фигурой с шестью гранями. Увидеть его можно, если посмотреть на прямоугольный бассейн, кирпич или спичечный коробок.

Эта фигура очень часто встречается в повседневной жизни, однако, нередко возникает необходимость узнать ее объем, что для многих представляет некоторые трудности. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.

Во многих других ситуациях возникает проблема, как найти объем параллелепипеда правильно.

Между тем вычислить это значение очень просто. Достаточно лишь знать ширину, длину и высоту предмета или объекта. И также необходимо знать формулу, с помощью которой и находят объем данной геометрической фигуры.

Объём параллелепипеда

Объём параллелепипеда можно находить тремя способами, принимая за основание этого параллелепипеда любую его грань, а за его высоту — расстояние между этой гранью и гранью, ей параллельной. На рисунке 1 изображено все $3$ способа нахождения объёма одного и того же параллелепипеда. На первом за основание берётся стороны $a$ и $b$, за высоту $c$. На втором за основание берётся стороны $c$ и $b$, за высоту $a$. На третьем за основание берётся стороны $a$ и $c$, за высоту $b$.

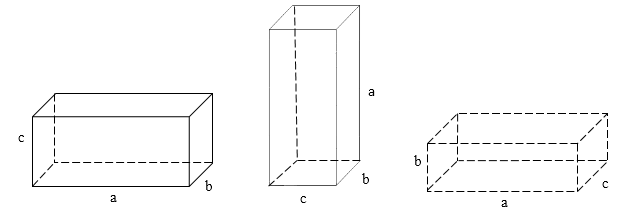Рисунок 1. Прямоугольный параллелепипед

Сначала мы находим объём прямоугольного параллелепипеда со сторонами основания и высотой равными 1 единицы (рисунок 2а). Объём данного параллелепипеда будет равен 1 кубической единице.

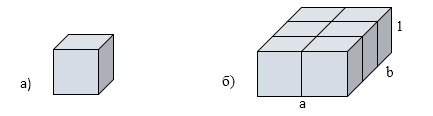Рисунок 2. Объем каждого твердого тела равен числу единичных кубиков

Теперь возьмём прямоугольный параллелепипед со сторонами основания $a$, $b$ и высотой $1$ (рисунок 2б), расположив данный параллелепипед и единичный куб так, чтобы их основания находились в одной плоскости, а сами многогранники были расположены по одну сторону от этой плоскости.

Тогда площади сечений, образованных при пересечении обоих многогранников любой плоскостью, параллельной плоскости основания этих многогранников, относятся как $(a\cdot b):1$. Это означает, что их объёмы также относятся как $(a\cdot b):1$, т.е.

откуда объём $V_{пар.}$ Прямоугольного параллелепипеда с измерениями $a$, $b$, $1$ равен $a\cdot b\cdot 1$, т.е.

Затем находим объём прямоугольного параллелепипеда с измерениями $a$, $b$, $c$, для чего прямоугольный параллелепипед с измерениями $a$, $b$, $c$ расположим так, чтобы грань со сторонами $1$ и $a$ первого параллелепипеда лежали в одной плоскости, и оба параллелепипеда находились по одну сторону от этой плоскости. Тогда площади сечений, образованных при пересечении обоих многогранников любой плоскостью, параллельной плоскости оснований этих многогранников, относятся как

Это означает, что их объёмы также относятся как $1:c$. А так как объёмы параллелепипеда с измерениями $1$, $a$, $b$ равен $ab$, то для объёма $VF$ прямоугольного параллелепипеда с измерениями $a$, $b$, $c$ выполняется соотношение

Откуда

Объем параллелепипеда через стороны и высоту

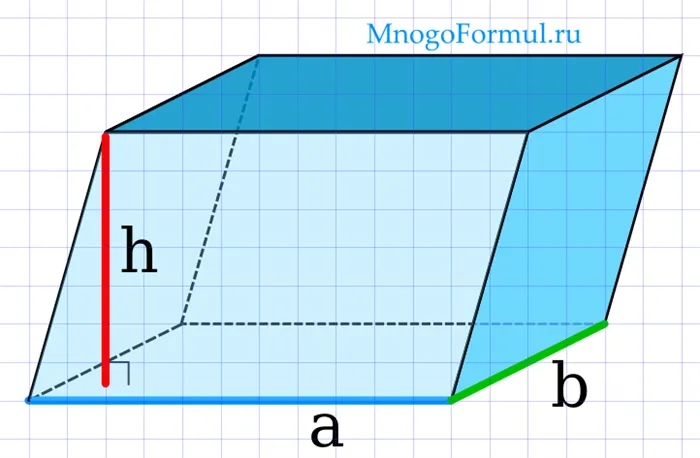
Можно вывести и другую формулу, которая имеет некоторое отличие. Это произведение площади основания и высоты. Формула выглядит следующим образом: V = S x h. Где h — высота параллелепипеда. S — площадь основания, которая является произведением двух сторон основания. Обычно обозначаются как a и b: S = a x b.Для расчета можно использовать любую из двух формул. Оба варианта верны и дают точные данные. Последний метод полезен, если вы уже знаете площадь основания. Если он неизвестен, проще перемножить три линейных размера одновременно, избежав тем самым ненужной процедуры.=>

Чтобы вычислить объем параллелепипеда, нужно знать, что это за фигура. Это призма, основанием которой является параллелограмм. Параллелепипед имеет 6 граней, каждая из которых является параллелограммом. Существует несколько типов элементов. Принцип расчета не имеет особых отличий, но сами цифры отличаются по внешнему виду. Таким образом, можно выделить следующие типы:

Также важно помнить, что каждый компонент формулы при расчете должен иметь одинаковую размерность. Если вы не будете соблюдать это простое правило, вы получите правильное значение p

Пример расчета

Не стоит думать, что основные математические формулы для определения объема геометрических фигур можно найти только на уроках математики. В большинстве случаев они пригодятся в дальнейшей жизни. Особенно в ремонтных или строительных работах, в дизайне и оформлении интерьера и во многих других ситуациях. В этом случае правильная формула имеет решающее значение.

Подведем итог: объем кубоида равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при каждом вращении и обороте. Результат не изменится.

— Бим, давай отведем обезьян в цирк, — Боб посмотрел на часы, — им пора ужинать. Большое спасибо, ребята! Вы и Бим помогли нам понять, что такое объем, что такое кубоид, как определить объем кубоида и выучить единицы измерения объема. Увидимся в цирке!

Формула расчета объема прямоугольного параллелепипеда

Прямоугольный параллелепипед – это геометрическое тело, у которого все грани являются прямоугольниками. Чтобы вычислить объем такого тела, нужно умножить длину, ширину и высоту.

Формула расчета объема прямоугольного параллелепипеда:

• V – объем;
• a – длина;
• b – ширина;
• h – высота.

Измерения длины, ширины и высоты должны быть взяты в одной единице измерения, например, метрах или сантиметрах. Результатом будет объем в кубических метрах или кубических сантиметрах.

Также можно выразить длину, ширину и высоту через диагонали грани прямоугольного параллелепипеда:

• V – объем;
• d₁, d₂, d₃ – диагонали граней.

Эта формула особенно удобна, когда неизвестны длина, ширина и высота, но известны диагонали граней.

Формула объема прямоугольного параллелепипеда

Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.

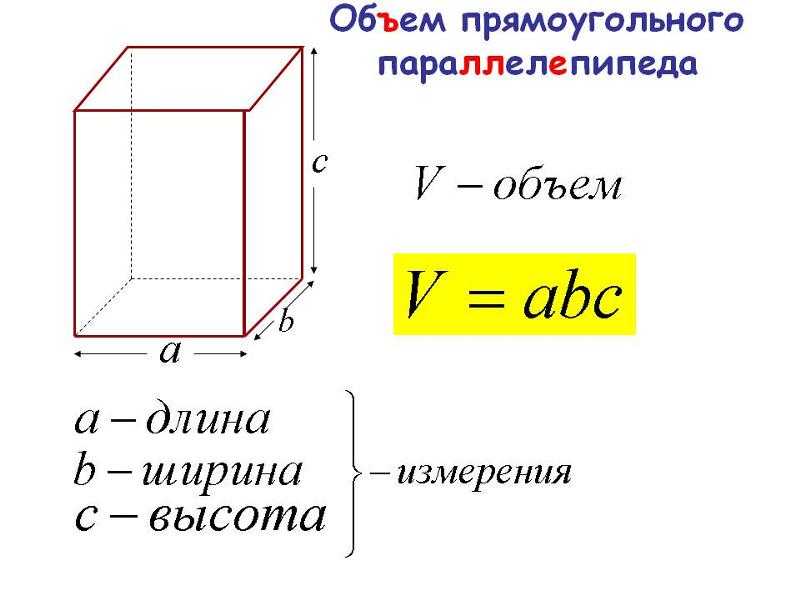
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.

Примечание 1
. Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).

Примечание 2
. Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.

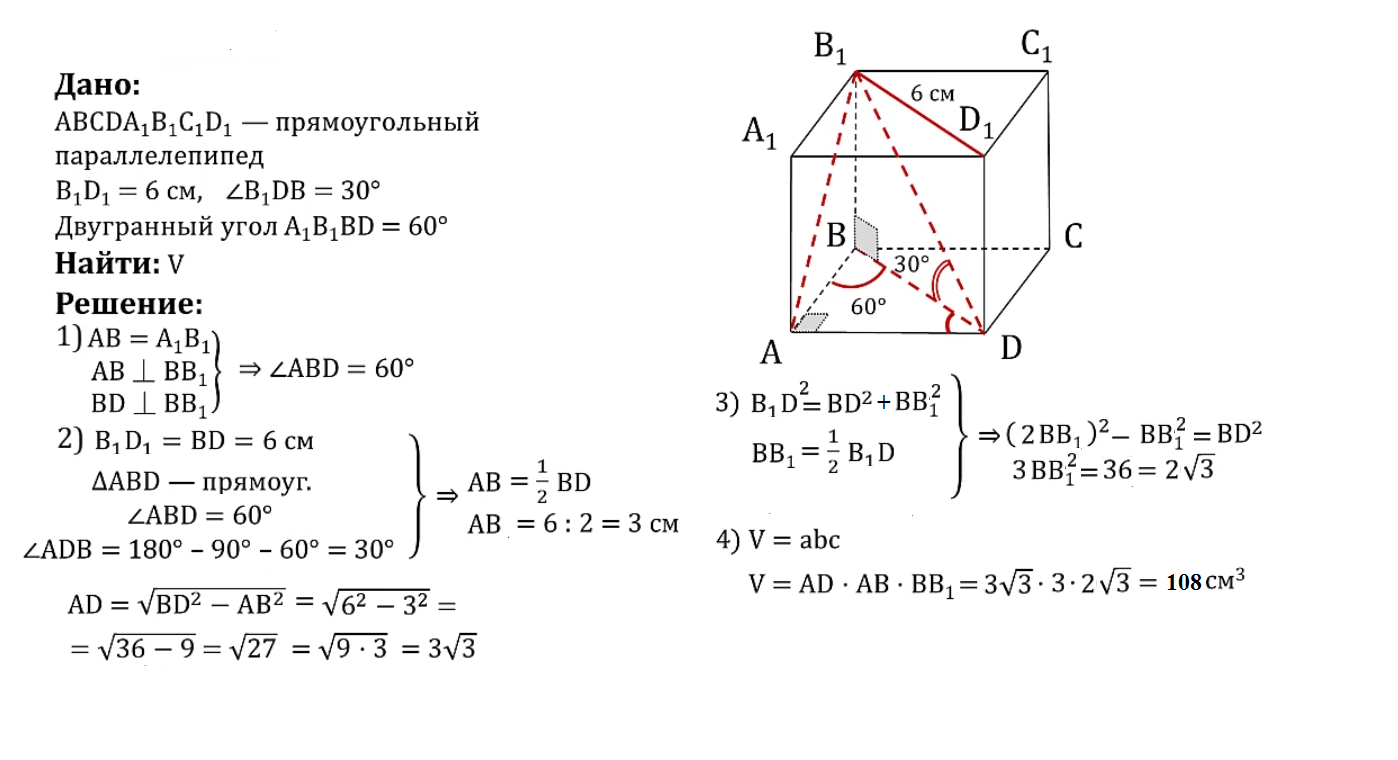
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.

Онлайн-калькулятор объема параллелепипеда

Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.

Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.

Формула вычисления объема параллелепипеда

1. Общая формула

Объем любого параллелепипеда равняется произведению площади его основания на высоту.

V = S_осн ⋅ h

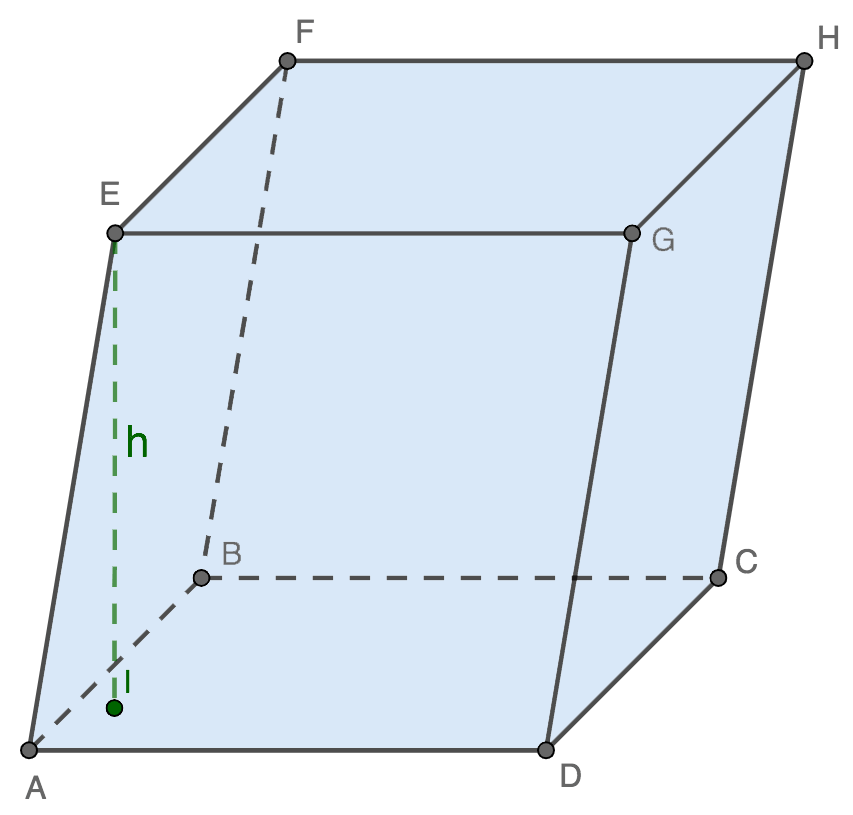
• S_осн – площадь основания (ABCD или EFHG, равны между собой);
• h – высота.

Данная формула справедлива для всех видов геометрической фигуры:

• наклонной – боковые грани не перпендикулярны основаниям;
• прямой – все боковые грани (4 шт.) являются прямоугольниками;
• прямоугольной – все грани (боковые и основания) являются прямоугольниками;
• ромбоэдра – все грани являются равными ромбами;
• куба – все грани представляют собой равные квадраты.

2. Объем прямоугольного параллелепипеда

Объем фигуры равен произведению его длины на ширину на высоту.

V = a ⋅ b ⋅ c

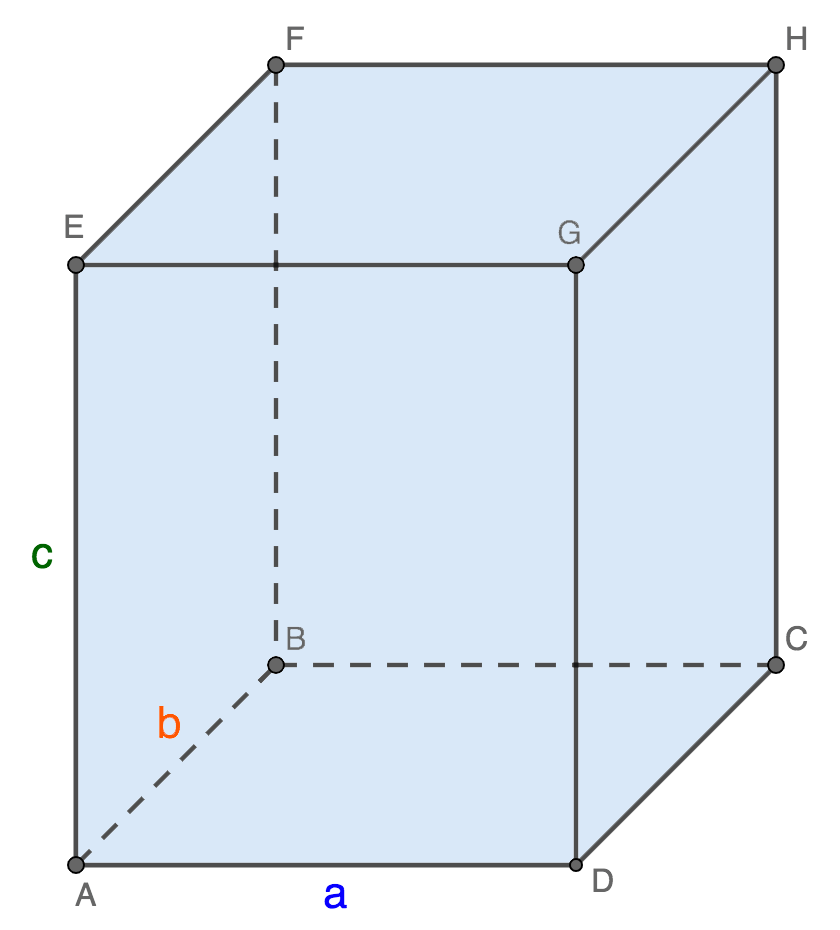
Формула следует из следующих утверждений:

• Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины (a) на ширину (b).
• Высота фигуры – это длина боковой грани (c).

Вычисление объема

Предположим, у нас есть вот такая прозрачная коробка и маленькие кубики с ребром $1$ $см.$

Чтобы найти объем коробки, заполним ее кубиками и посчитаем их количество:

У нас получился вот такой прямоугольный параллелепипед. Его длина — $4$ кубика, ширина — $3$ кубика, а высота — $2$ кубика.

Объем всей фигуры будет равен $24$ кубикам или $24$ $см^3.$

формула объема

Объем обозначается буквой $V$. В буквенном виде формулу объема можно записать так:$$V=\textcolor{coral}{a}\textcolor{blue}{b}\textcolor{orange}{c}$$

{"questions":[{"content":"Найдите объем коробки, если ее длина — $\\textcolor{coral}{10 \\space см}$, ширина — $\\textcolor{blue}{5 \\space см}$, а высота — $\\textcolor{orange}{20 \\space см}.$`image-1``choice-15`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/11/box-.svg","width":"300"},"choice-15":{"type":"choice","options":,"answer":}},"step":1,"hints":}]}

Объем куба

Все измерения куба одинаковы, поэтому формула объема куба будет выглядеть так:$$V=\textcolor{coral}{a}^3$$

куб числа

Третью степень числа ($n^3$) часто называют кубом числа $n.$

{"questions":,"answer":},"image-2":{"type":"image","url":""}},"step":1,"hints":}]}