Как найти площадь прямоугольного параллелепипеда?

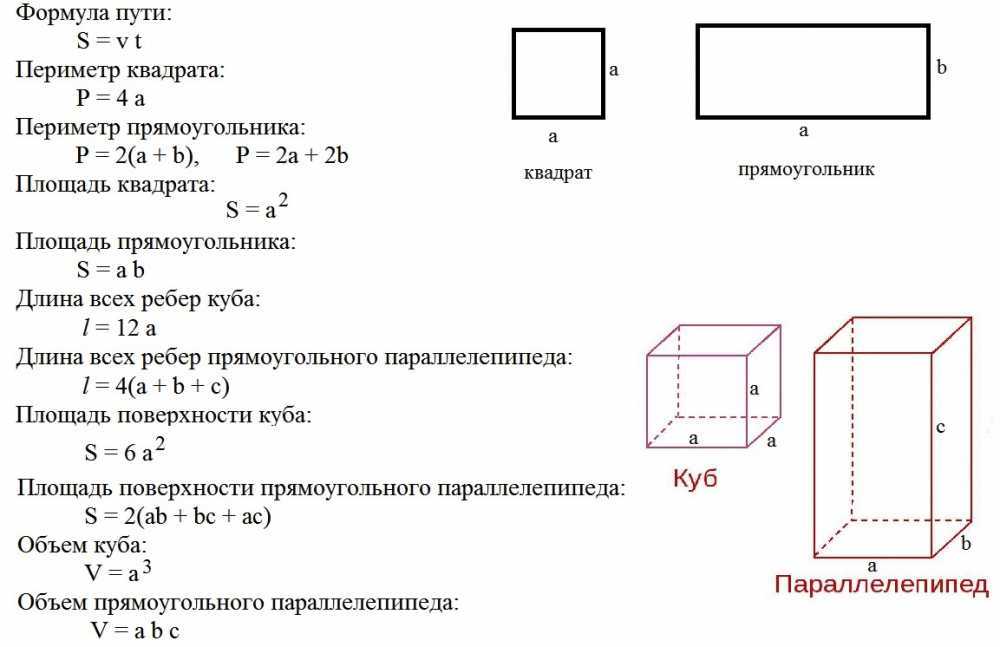
Площадь поверхности параллелепипеда как найти?

Параллелепипед — это призма, в основании которой находится параллелограмм. Противоположные стороны параллелепипеда равны. Соответственно, у них будут и равные площади. Всего у параллелепипеда 6 граней, значит:

Sобщ = 2(S1+S2+S3)

Идем дальше. Примем, что ребра параллелограмма равны a, b и с. Где a, b — стороны основания (образуют S1), а с — высота параллелограмма. b и с образуют S2, а c и a образуют S3.

Далее: существует несколько различных случаев:

1) Если все шесть граней параллелепипеда являются прямоугольниками — то такой параллелепипед называется прямоугольным. И его площадь высчитывается по формуле:

2) Если четыре из шести граней параллелограмма являются прямоугольниками, то такой параллелепипед называется прямым. Его площадь считается не только через длину его ребер, но и через величину непрямого угла между сторонами параллелограмма, не являющегося прямоугольником:

Sобщ = 2(S1+S2+S3) = 2(absinX + сb + aс)

Sобщ = 2(S1+S2+S3) = 2(a^a+а^2+a^2)=6a^2, где а — ребро куба.

Общая формула площади поверхности параллелограмма в полном варианте применяется в тех случаях, когда он не является прямоугольным. Ребра такой призмы расположены не под прямым углом друг к другу, а значит синус этих углов не равен единице, как в предыдущих случаях, когда мы его просто не указывали.

Если допустить, что углы между ребрами параллелограмма равны:

угол между а и b = X
угол между а и c = Y
угол между c и b = Z

Тогда:

Sобщ = 2(S1+S2+S3) = 2(absinX + сbsinZ + aсsinY)

Далее можно упомянуть еще один вид параллелограммов: те, у которых лишь две стороны являются прямоугольниками. Допустим, что S1 — это площадь прямоугольника в основании. Тогда:

Sобщ = 2(S1+S2+S3) = 2(absinX + сbsinZ + aсsinY) = 2(ab + сbsinZ + aсsinY), т.к. Х=90 градусов и sinX=1.

Вот как-то так)

Измерения прямоугольного параллелепипеда и его свойства

Что такое прямоугольный параллелепипед — определение
Свойства параллелепипеда, какими обладают противолежащие грани
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Как найти диагональ и ширину прямоугольного параллелепипеда

Что такое прямоугольный параллелепипед — определение

Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.

Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.

В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

прямоугольный;
прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
ромбоэдр — шестигранная призма, грани которой — это ромбы;
куб — состоит из квадратных граней.

Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.

Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.

Прямоугольный параллелепипед, как и любой другой, состоит из:

основания;
граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
диагоналей — отрезков, соединяющих противоположные вершины;
диагоналей граней;
высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.

В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.

Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.

Свойства параллелепипеда, какими обладают противолежащие грани

Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:

Противолежащие грани равны друг другу и попарно параллельны.
Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
Фигура симметрична относительно середины диагонали.
Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.

Все стороны — прямоугольники.
Все углы, состоящие из двух граней, равны 90°.
Любую сторону можно принять за основание.
Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.

где V — объем, a — длина, b — ширина, h — высота.

Площадь боковой поверхности равна сумме площадей боковых граней.

Площадь полной поверхности равна сумме площадей боковых граней и оснований.

Как найти диагональ и ширину прямоугольного параллелепипеда

В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:

Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:

Длина, ширина и высота, как правило, вычисляются через формулу объема:

Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.

Нахождение площадей фигур

Рассмотрим, как находятся площади, могущие составлять грани параллелепипеда.

Площадь квадрата равна произведению его стороны самой на себя. Формула площади квадрата имеет вид S = a*a = a^2.
Прямоугольника — вычисляется с помощью умножения большей его стороны (длины) на меньшую его сторону (ширину). Формула площади прямоугольника имеет вид S = a*b.
Параллелограмма — найти сложнее и имеется несколько различных способов. Наиболее часто в математике применяются формулы для нахождения с помощью стороны и опущенной на неё высоты или двух сторон и синуса угла между ними. Записываются они следующим образом: S = a*h, S = a*b*sin (ab).

Рассмотрим на примерах как найти площадь каждой из рассматриваемых нами фигур.

1. Длина стороны квадрата равна 1600 метров. Определим его площадь.

S = a*a, отсюда в искомом случае S = 1600*1600 = 2 560 000 метров квадратных.

2. Стороны прямоугольника равны 90 и 200 метров соответственно. Определим его S.

S = a*b, следовательно в нашем варианте получится S = 90*200 = 18 000 метров квадратных.

3. С параллелограммом рассмотрим два случая нахождения.

Сторона равна 300 метров, а опущенная на неё высота 250 метров. Тогда получится:

S = a*h = 300*250 = 75 000 метров квадратных.

Второй вариант — стороны равны 550 и 200 метров соответственно. Угол между ними 30 градусов. Имеем:

S = a*b*sin (ab) = 550*200*sin 30 = 110 000*0.5 = 55 000 квадратных метров.

Как видно из примеров, приведённых выше, никаких сложностей нет.

Формула нахождения полной площади

В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:

$S=2\cdot(a\cdot b+a\cdot c+b\cdot c)$

где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.

Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA₁B₁C₁D₁.

Рисунок 1

Полная площадь его поверхности равняется сумме площадей всех граней: $S_{пар}=S_{AA_1D_1D}+S_{DD_1C_1C}+S_{CC_1B_1B}+S_{BB_1A_1A}+S_{ABCD}+S_{A_1B_1C_1D_1}$

Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:

$S_{пар}=2\cdot\left(S_{AA_1D_1D}+S_{BB_1A_1A}+S_{ABCD}\right)$

Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:

$S_▭=a\cdot b$

У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA₁. Для удобства обозначим их как a, b и c соответственно.

Рисунок 2

Таким образом:

$S_{ABCD}=a\cdot b$

$S_{AA_1D_1D}=a\cdot c$

$S_{BB_1A_1A}=b\cdot c$

Подставим данные значения в обозначенную выше формулу площади параллелепипеда:

$S_{пар}=2\cdot\left(a\cdot b+a\cdot c+b\cdot c\right)$

Диагональ параллелепипеда

Особое внимание этому элементу фигуры принято уделять по причине того, что он часто используется для вычисления объема и площади поверхности, совместно с двумя другими линейными параметрами. Прямоугольный параллелепипед определяется тремя линейными характеристиками

Геометрический элемент

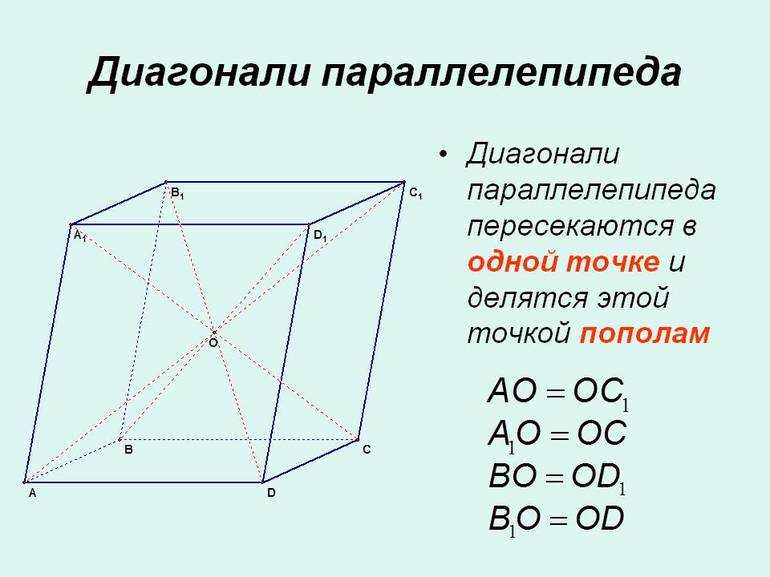
Чтобы построить диагональ параллелепипеда, необходимо рассмотреть его произвольную вершину. Она соединена ребрами с тремя другими. Еще 3 можно соединить с помощью диагоналей граней. В итоге остается лишь одна вершина, которая с исходной соединяется отрезком, проходящим через весь объем фигуры. Этот отрезок называется диагональю параллелепипеда.

Из этих рассуждений несложно понять, сколько диагоналей у параллелепипеда — 4. Их особым свойством является равенство длин. Оно следует из факта симметричности фигуры.

Вывод формулы

Для определения длины диагонали параллелепипеда следует ввести некоторые обозначения. Все вершины одного основания будут A, B, C, D, а их аналоги — A1, B1, C1, D1.

Пусть следует найти диагональ AC1. Дополнительными обозначениями сторон, которые облегчат процедуру вывода формулы, будут:

a — сторона AB;
b — сторона AD;
h — высота параллелепипеда, равна длине сторон AA1, BB1, CC1 и DD1.

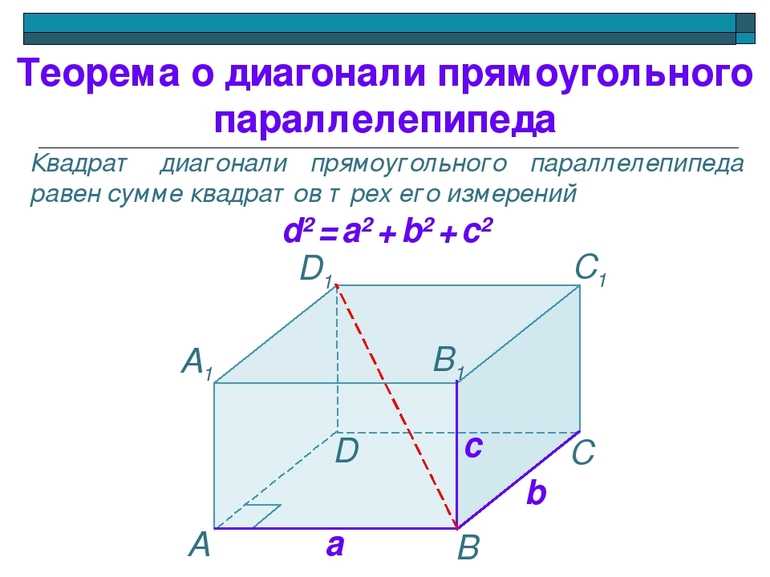
Сначала необходимо рассмотреть треугольник ABC, который лежит в плоскости одного из оснований. В нем угол B является прямым, а сторона AC — гипотенуза. Если применить теорему Пифагора, получится следующий результат для длины AC: AC = (a 2 + b 2 )^0,5.

Теперь следует обратить внимание на фигуру, которая ограничена вершинами A, C и C1. Это прямоугольный треугольник, в котором стороны AC и CC1 являются катетами, а диагональ AC1 — гипотенуза

Используя введенные обозначения и снова применяя теорему греческого философа: AC1 = (AC 2 + CC1 2 )^0,5 = (a 2 + b 2 + h 2 )^0,5.

Случай куба

Все рассуждения касательно вывода формулы диагонали параллелепипеда остаются верными для куба. Поскольку фигура обладает высокой симметрией в пространстве, для однозначного определения всех ее параметров необходимо знать лишь одну-единственную сторону квадрата. Пусть это будет a. Общая формула для длины диагонали имеет вид: AC1 = (a 2 + b 2 + h 2 )^0,5.

Если подставить сюда вместо b и h длину стороны a, получается следующее простое равенство: AC1 = a*(3)^0,5.

В кубе его объемная диагональ приблизительно в 1,225 раза больше, чем аналогичный отрезок для грани.

Формула нахождения полной площади

(S=2cdot(acdot b+acdot c+bcdot c))

где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.

Рисунок 1

Полная площадь его поверхности равняется сумме площадей всех граней: (S_{пар}=S_{AA_1D_1D}+S_{DD_1C_1C}+S_{CC_1B_1B}+S_{BB_1A_1A}+S_{ABCD}+S_{A_1B_1C_1D_1})

(S_{пар}=2cdotleft(S_{AA_1D_1D}+S_{BB_1A_1A}+S_{ABCD}right))

(S_▭=acdot b)

Рисунок 2

Таким образом:

(S_{ABCD}=acdot b)

(S_{AA_1D_1D}=acdot c)

(S_{BB_1A_1A}=bcdot c)

Подставим данные значения в обозначенную выше формулу площади параллелепипеда:

(S_{пар}=2cdotleft(acdot b+acdot c+bcdot cright))

Определения

Параллелепипед – это фигура в пространстве, которая состоит из шести четырехугольников.

Каждый четырехугольник – это грань параллелепипеда. Среди граней различают четыре боковые и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.

Стороны граней – это ребра. У параллелепипеда всего 12 ребер.

Параллелепипед имеет 8 вершин, для их обозначения используют заглавные латинские буквы.

Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань прямоугольного параллелепипеда – это прямоугольник, у которого противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда также равны.

Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.

Рис. 1. Прямоугольный параллелепипед

Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.

Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.

Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.

Площадь поверхности параллелепипеда через стороны

Для прямоугольного параллелепипеда площадь поверхности определяется по формуле:

$S = 2 cdot (a cdot b + b cdot h + a cdot h)$, здесь

$a, b$ — отзыв страны параллепипеда;

$h$ — высота параллельной трубы.

Научись программировать Получите навыки для отличной карьеры в ИТ под руководством ведущих специалистов

Разберём пример на ходень полной продажи праллелепипеда.

Пример 1

Задача

Стороны основания прямоугольного параллелепипеда равны $a = 3$ см и $b = 7$ см, а его высота $h$ равна $4$ см. Чему ревана полная площадь профессия параллелепипеда?

Решение:

Мы используем приведенную выше формулу:

$S = 2 cdot (3 cdot 4 + 7 cdot 4 + 3 cdot 7) = 122$ кв см.

Результаты совпадают с решением онлайн-калькулятора, значит, ответ правильный.

Также с помощью следующего онлайн-калькулятора можно рассчитать площадь боковой поверхности прямоугольного параллелепипеда.

Формулы объема и поверхности

Объем выражает количество чего-то (например, воды), которое нам нужно, чтобы заполнить форму.
Космические фигуры имеют только объем. Плоские фигуры (треугольники, квадраты) не имеют объема. Стандартное обозначение для тома — V.

Прямоугольный параллелепипед

Прямоугольный параллелепипед имеет 6 граней, которые являются прямоугольниками. Если стороны прямоугольника внизу равны а и
b, а высота параллелепипеда c
(третье ребро прямоугольного параллелепипеда).

Параллелепипед

Параллелепипед образован 6 параллелограммами.
Если площадь дна равна А, а высота
параллелепипед h. Формула объема:

$V = A \cdot h$

Пирамида

Пирамида — это фигура с многоугольным основанием (треугольник, квадрат, прямоугольник), соединенным с одной точкой, называемой вершиной.

Площадь боковой поверхности = $\pi\cdot r \cdot l$

Общая площадь поверхности = $\pi\cdot r(r + l)$

Сфера

Сфера — это поверхность полностью круглого шара. Каждая сфера имеет центральную точку, называемую «центром» сферы. Радиус — это длина от центра до любой точки на поверхности сферы. Объем сферы радиусом r:
92 \cdot ч$

Площадь изогнутой (боковой) поверхности = $2\cdot\pi\cdot r \cdot h$

Общая площадь поверхности = $2\cdot\pi\cdot r(h + r)$

Викторина: Объем и площадь поверхности

Наклонный параллелепипед: свойства, формулы и задачи репетитора по математике

Параллелепипедом называется четырехугольная призма, в основаниях которой лежат параллелограммы. Высотой параллелепипеда называют расстояние между плоскостями его основаниями. На рисунке высота показана отрезком . Различают два вида параллелепипедов: прямой и наклонный. Как правило, репетитор по математике сначала дает соответствующие определения для призмы, а затем переносит их на параллелепипед. Мы сделаем также.

Напомню, что призма называется прямой, если ее боковые ребра перпендикулярны основаниям, если перпендикулярности нет – призму называют наклонной. Эту терминологию наследует и параллелепипед. Прямой параллелепипед – ни что иное, как разновидность прямой призмы, боковое ребро которой совпадает с высотой. Сохраняются определения таких понятий, как грань, ребро и вершина, являющиеся общими для всего семейства многогранников. Появляются понятие противоположные грани. У параллелепипеда 3 пары противоположных граней, 8 вершин ти 12 ребер.

Свойства наклонного параллелепипеда:

1) Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
3) Каждый параллелепипед состоит из шести равных по объему треугольных пирамид. Чтобы показать их ученику репетитор по математике должен отрезать от параллелепепеда половинку его диагональным сечением и разбить ее отдельно на 3 пирамиды. Их основания должны лежать в разных гранях исходного паралеллепипеда. Репетитор математики найдет применение этого свойства в аналитической геометрии. Оно используется для вывода объема пирамиды через смешанное произведение векторов.

Формулы объема параллелепипеда:
1) , где — площадь основания, h – высота.
2) Объем параллелепипеда равен произведению площади поперечного сечения на боковое ребро .Репетитору по математике: Как известно, формула является общей для всех призм и если репетитор уже доказал ее, нет смысла повторять тоже самое для параллелепипеда. Однако в работе со учеником среднего уровня (слабому формула не пригодиться) преподавателю желательно действовать с точностью до наоборот. Призму оставить в покое, а для параллелепипеда провести аккуратное доказательство.
3) , где –объем одной из шести треугольных пирамиды из которых состоит параллелепипед.
4) Если , то

Площадью боковой поверхности параллелепипеда называется сумма площадей всех его граней:
Полная поверхность параллелепипеда – это сумма площадей всех его граней, то есть площадь + две площади основания: .

О работе репетитора с наклонным параллелепипедом:
Задачами на наклонный параллелепипед репетитор по математике занимается не часто. Вероятность их появления на ЕГЭ достаточно мала, а дидактика неприлично бедная.

Более-менее приличная задача на объем наклонного параллелепипеда вызывает серьезные проблемы, связанные с пределением расположения точки Н — основания его высоты.

В этом случае репетитору по математике можно посоветовать обрезать параллелепипед до одной из шести его пирамид (о которых идет речь в свойстве №3), попробовать найти ее объем и умножить его на 6.

Задачи репетитора по математике:
1) Грани параллелепипеда равные роибы со стороной 2см и острым углом . Найти объем параллелепипеда.
2) В наклонном параллелепипеде боковое ребро равно 5см. Сечение, перпендикулярное ему, является четырехугольником со взаимно перпендикулярными диагоналями, имеющими длины 6см и 8 см. Вычислить объем паралеллепипеда.

3) В наклонном параллелепипеде известно, что , а в онованием ABCD является ромб со стороной 2см и уголом . Определите объем параллелепипеда.

Репетитор по математике, Александр Колпаков

Как найти площадь поверхности параллелепипеда

Призма, у которой все стороны являются параллелограммами, и есть параллелепипед. Коробка, холодильник, здания, аквариум, кусочек сахара-рафинада – вот немногие примеры параллелепипеда в нашей повседневной жизни.

Разновидность, свойства параллелепипеда

Различают прямой и наклонный параллелепипед.

Прямой – это тот, ребра которого перпендикулярны основанию плоскости. Если основанием является прямоугольник, тогда фигура называется прямоугольным параллелепипедом. Если основанием и боковыми гранями является квадрат – куб.

Наклонный параллелепипед имеет наклон боковых граней к основанию под углом, отличным от 90 градусов.

Свойства параллелепипеда:

Противоположные грани равны и параллельны.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов 3-х его измерений, т.е. D^2=a^2+b^2+c^2.
Все диагонали пересекаются в одной точке, делящей их пополам.
Параллелепипед симметричен по отношению к середине его диагонали.

Площадь поверхности параллелепипеда

Как известно, существует несколько разновидностей параллелепипеда, поэтому и формулы для нахождения площади полной поверхности будут различаться.

Прямоугольный параллелепипед

У прямоугольного параллелепипеда основания и боковые грани – прямоугольники.

В данном случае используется формула S(п)=2(a*b+b*c+a*c).

Куб является частным случаем параллелепипеда. У него все стороны равны. Воспользовавшись формулой выше, получаем S(п)=2(a*a+a*a+a*a). В результате преобразования можно получить сокращенную версию формулы для нахождения площади полной поверхности куба S(п)=6*a^2.

Прямой параллелепипед

В то время, когда у прямоугольного параллелепипеда основанием является прямоугольник, прямой может иметь там любой параллелограмм, будь то квадрат или ромб. Именно поэтому формула для нахождения площади полной поверхности такой фигуры будет иной: S(п)=S(б)+2S(о), где S(о) – площадь основания, S(б) – площадь боковой поверхности.

Площадь основания S(о) будет зависеть от того, какая фигура лежит в основании.

В свою очередь, площадь боковой поверхности рассчитывается, как S(б)=P(о)*h, где P(о) — периметр основания, h – высота.

Как найти площадь поверхности параллелепипеда — пример

Основанием прямого параллелепипеда служит ромб. Меньшая его диагональ равна 5 см, большая диагональ – 9 см, периметр равен 20 см. Найти площадь полной поверхности параллелепипеда, если его высота равна 6 см.

Для решения задачи понадобится формула S(п)=S(б)+2S(о).

S(б)=P(о)*h=20*6=120 см^2

S(о)=(d1+d2)/2=(5+9)/2=7см^2

Подставив данные в формулу, получаем S(п)=120+2*7=134 см^2.

Человека окружает множество вещей-параллелепипедов. Системный блок компьютера, кирпич, шкаф, различные архитектурные сооружения. Даже не замечая, параллелепипед занял значимое место в современном мире.

Что такое площадь поверхности параллелепипеда

Определение

Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Частный случай этой геометрической фигуры — прямой параллелепипед, у которого все грани являются прямоугольниками.

В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.

Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.

Формула площади поверхности параллелепипеда

ÃÂÃÂ¾ ÃÂÃÂ°ÃÂº ÃÂºÃÂ°ÃÂº ÃÂ¿ÃÂÃÂ¾ÃÂÃÂ¸ÃÂ²ÃÂ¾ÃÂ¿ÃÂ¾ÃÂ»ÃÂ¾ÃÂ¶ÃÂ½ÃÂÃÂµ ÃÂ³ÃÂÃÂ°ÃÂ½ÃÂ¸ ÃÂ¿ÃÂÃÂÃÂ¼ÃÂ¾ÃÂÃÂ³ÃÂ¾ÃÂ»ÃÂÃÂ½ÃÂ¾ÃÂ³ÃÂ¾ ÃÂ¿ÃÂ°ÃÂÃÂ°ÃÂ»ÃÂ»ÃÂµÃÂ»ÃÂµÃÂ¿ÃÂ¸ÃÂ¿ÃÂµÃÂ´ÃÂ° ÃÂÃÂ°ÃÂ²ÃÂ½ÃÂ ÃÂ¼ÃÂµÃÂ¶ÃÂ´ÃÂ ÃÂÃÂ¾ÃÂ±ÃÂ¾ÃÂ¹, ÃÂÃÂ¾: S1=S2S_1=S_2, S3=S4S_3=S_4, S5=S6S_5=S_6.

ÃÂÃÂ¾ÃÂÃÂºÃÂ¾ÃÂ»ÃÂÃÂºÃÂ ÃÂ³ÃÂÃÂ°ÃÂ½ÃÂÃÂ¼ÃÂ¸ ÃÂ´ÃÂ°ÃÂ½ÃÂ½ÃÂ¾ÃÂ³ÃÂ¾ ÃÂ¿ÃÂ°ÃÂÃÂ°ÃÂ»ÃÂ»ÃÂµÃÂ»ÃÂµÃÂ¿ÃÂ¸ÃÂ¿ÃÂµÃÂ´ÃÂ° ÃÂÃÂ²ÃÂ»ÃÂÃÂÃÂÃÂÃÂ ÃÂ¿ÃÂÃÂÃÂ¼ÃÂ¾ÃÂÃÂ³ÃÂ¾ÃÂ»ÃÂÃÂ½ÃÂ¸ÃÂºÃÂ¸, ÃÂÃÂ¾ ÃÂ¸ÃÂ ÃÂ¿ÃÂ»ÃÂ¾ÃÂÃÂ°ÃÂ´ÃÂ¸ ÃÂÃÂ°ÃÂ²ÃÂ½ÃÂ ÃÂÃÂ¾ÃÂ¾ÃÂÃÂ²ÃÂµÃÂÃÂÃÂÃÂ²ÃÂµÃÂ½ÃÂ½ÃÂ¾:

S1=S2=abS_1=S_2=abS3=S4=bcS_3=S_4=bcS5=S6=acS_5=S_6=ac

ÃÂÃÂµ ÃÂ·ÃÂ½ÃÂ°ÃÂµÃÂÃÂµ, ÃÂ³ÃÂ´ÃÂµ ÃÂ·ÃÂ°ÃÂºÃÂ°ÃÂ·ÃÂ°ÃÂÃÂ ÃÂ·ÃÂ°ÃÂ´ÃÂ°ÃÂÃÂ ÃÂ¿ÃÂ¾ ÃÂ³ÃÂµÃÂ¾ÃÂ¼ÃÂµÃÂÃÂÃÂ¸ÃÂ¸? ÃÂÃÂ±ÃÂÃÂ°ÃÂÃÂ¸ÃÂÃÂµÃÂÃÂ ÃÂº ÃÂ½ÃÂ°ÃÂÃÂ¸ÃÂ¼ ÃÂÃÂºÃÂÃÂ¿ÃÂµÃÂÃÂÃÂ°ÃÂ¼ ÃÂ² ÃÂ´ÃÂ°ÃÂ½ÃÂ½ÃÂ¾ÃÂ¹ ÃÂ¾ÃÂ±ÃÂ»ÃÂ°ÃÂÃÂÃÂ¸!

Вот все, что вам нужно знать о прямоугольном параллелепипеде

Как называются коробки для обуви, книги и кирпичи? Это прямоугольник или параллелограмм? Это прямоугольный параллелепипед.

Что такое параллелепипед?

Параллелепипед состоит из шести параллелограммов. Это трехмерная форма. Слово «параллелепипед» восходит к параллелепипеду , греческому слову, означающему тело, имеющее параллельные тела. Параллелепипед состоит из 6 граней, похожих на параллелограмм, 12 ребер и восьми вершин. Некоторые специальные виды параллелепипедов куб, ромб и прямоугольный параллелепипед.

Что такое прямоугольный параллелепипед?

Прямоугольный параллелепипед, более известный как параллелепипед, представляет собой параллелепипед с прямоугольными гранями.

Каковы характеристики прямоугольного параллелепипеда?

Прямоугольный параллелепипед имеет следующие характеристики: –

Прямоугольный параллелепипед представляет собой трехмерную форму.
Состоит из шести параллелограммов прямоугольной формы.
Он также известен как прямоугольный параллелепипед.
Все противоположные грани равны и параллельны.
Параллельные ребра имеют одинаковую длину.
Диагональ, проходящая вдоль каждой грани, называется диагональю грани.
Три грани прямоугольного параллелепипеда видны одновременно.
Шестигранник означает многогранник, состоящий из шести граней.

Что такое формулы прямоугольного параллелепипеда?

Прямоугольный параллелепипед — трехмерная фигура. Три измерения — это длина, высота и ширина, далее обозначаемые как l, h и b соответственно. Формулы прямоугольного параллелепипеда, которые используются для расчета площади его боковой поверхности, площади поверхности, диагонали и объема, следующие:0006

Рассмотрим коробку из-под обуви. У коробки для обуви есть шесть сторон. Допустим, A и B — две противоположные боковые грани, C и D — две другие противоположные боковые грани, а E и F — верхняя и нижняя грани.

Общая площадь поверхности или TSA-

Общая площадь поверхности прямоугольного параллелепипеда – это площадь поверхности всех его граней. Это означает, что это общая площадь шести прямоугольных граней.

Таким образом, общая площадь поверхности прямоугольного параллелепипеда = 2 × площадь A + 2 × площадь C + 2 × площадь D.

(Поскольку B, D и F равны A, C и E)

TSA = 2 × площадь параллелограмма + 2 × площадь параллелограмма C + 2 × площадь параллелограмма.

TSA = 2× L × B + 2 × B × H+ 2 × H × L.

TSA = 2( LB + BH + HL).

Площадь боковой поверхности или LSA-

Площадь боковой поверхности прямоугольного параллелепипеда означает площадь всех сторон прямоугольного параллелепипеда. Это произведение высоты и периметра основания.

Площадь боковой поверхности прямоугольного параллелепипеда = периметр основания × высота.

(Основой прямоугольного параллелепипеда является прямоугольник. Следовательно, его периметр будет равен периметру прямоугольника)

LSA = 2 (длина + ширина) × высота.

LSA = 2 (lh+bh).

Кроме того, общую площадь поверхности можно рассчитать как

TSA = LSA + 2LW.

Объем или V-

Объем прямоугольного параллелепипеда относится к пространству, занимаемому прямоугольным параллелепипедом.

Объем прямоугольного параллелепипеда = площадь основания × высота.

(Так как основание прямоугольного параллелепипеда — прямоугольник. Следовательно, его объем будет равен объему прямоугольника)

V = L×b×h.

V = LBH

Формула диагонали –

Диагональ прямоугольного параллелепипеда может быть определена как прямая, соединяющая два противоположных угла прямоугольного параллелепипеда своей вершиной.

Длина диагонали прямоугольного параллелепипеда = √ l2 + b2 + h3

Заключение

Определение прямоугольного параллелепипеда — это трехмерная фигура, состоящая из шести параллелограммов прямоугольной формы. Это особый вид параллелепипеда, в котором все параллелограммы прямоугольной формы. Он широко известен как кубоид. Это многогранник с шестью прямоугольными гранями, известный как шестигранник.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
Высота прямого параллелепипеда равна длине бокового ребра.
Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Площадь боковой поверхности прямого параллелепипеда Sб = Ро*hРо — периметр основания h — высота
Площадь полной поверхности прямого параллелепипеда Sп = Sб+2SоSо — площадь основания
Объем прямого параллелепипеда V = Sо*h

Площадь поверхности параллелепипеда как найти?

Измерения прямоугольного параллелепипеда и его свойства

Что такое прямоугольный параллелепипед — определение

Свойства параллелепипеда, какими обладают противолежащие грани

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда

Как найти диагональ и ширину прямоугольного параллелепипеда

Нахождение площадей фигур

Формула нахождения полной площади

Диагональ параллелепипеда

Геометрический элемент

Вывод формулы

Случай куба

Формула нахождения полной площади

Определения

Площадь поверхности параллелепипеда через стороны

Формулы объема и поверхности

Прямоугольный параллелепипед

Параллелепипед

Пирамида

Сфера

Наклонный параллелепипед: свойства, формулы и задачи репетитора по математике

Как найти площадь поверхности параллелепипеда

Прямоугольный параллелепипед

Прямой параллелепипед

Что такое площадь поверхности параллелепипеда

Формула площади поверхности параллелепипеда

Вот все, что вам нужно знать о прямоугольном параллелепипеде

Прямой параллелепипед

Похожие записи:

Похожие записи: