Средние линии

Как сформулировать и доказать утверждения о свойствах параллелограмма, теоремы о признаках данной фигуры

Параллелограммом называют четырёхугольник (фигура, что состоит из четырёх точек и отрезков, последовательно их соединяющих), у которого противоположные стороны попарно параллельны. Его свойства впервые детально изучали греческие математики Евклид и Пифагор. Конец эпохи Средневековья принёс людям полную теорию об этой фигуре.

…

История возникновения термина

О некоторых видах четырёхугольников, квадратов, прямоугольников, равносторонних и прямоугольных трапеций знали ещё давно.

Термин «параллелограмм» греческого происхождения, считают что его придумал Евклид (приблизительно 300 годов до нашей эры). Ещё известно, что эта фигура и её свойства были знакомы ученикам школы Пифагора, раньше их называли пифагорейцами.

В «Началах» Евклида приведена следующая теорема: в параллелограмме противоположные стороны равны, а диагонали разделяют его по половине. Но в данной книге не было написано о свойствах точки их сечения. Ещё этот учёный не упоминает о прямоугольнике и ромбе.

Полную теорию сделали только в конце Средневековья, а в книгах она появилась в семнадцатом столетии. Теоремы и свойства параллелограмма основывались на аксиомах Евклида.

Нужно сказать, что Евклид, как и большинство математиков того времени, для названия отрезка, который соединяет противоположные вершины четырёхугольника или прямоугольника, использовал другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои мысли основывали на вписании круга в прямоугольник. В Средние века для названия приведённых отрезков использовали оба термина. Только в семнадцатом столетии «диагональ» стала общепринятой.

Доказательство признаков фигуры

На следующем рисунке изображён параллелограмм ABCD, где AB параллельно CD и AD параллельно BC:

Сумма любых двух соседних углов параллелограмма равна 180 градусам — это первая подсказка о том, как сформулировать и доказать утверждения о признаках параллелограмма.

На этом рисунке углы A и B фигуры ABCD есть внутренними односторонними углами для параллельных прямых AD и BC . Поэтому углы A + B равны 180 градусам. Аналогично это свойство можно привести для любой другой пары соседних (если вершины есть концами одной и той же стороны) углов.

Теорема признаков паралелограмма

Теорема признаков параллелограмма гласит, что это выпуклый четырёхугольник. Исходя из предыдущего правила, угол А намного меньше 180 градусов, как и B, C, D, поэтому его называют опухлым четырёхугольником. Диагонали этой фигуры могут пересекаться.
У параллелограмма противоположные стороны и углы равны.

Диагональ АС разбивает фигуру на два треугольника ABC и ADC. АС — общая сторона двоих треугольников и САD эквивалентен АСВ также с САВ и АСD. Тогда ∆АВС = ∆СDA, по стороне и двумя прилегающими углами. Это значит, что АВ=СD, BC=AD и B=D, как соответствующие элементы в различных треугольниках.

Теорема о диагоналях

Периметр (сумма длин всех сторон четырёхугольника, которую обозначают буквой Р) параллелограмма эквивалентен 2 (АВ +ВС) или АВ + ВС + СD + DA.
Теорема о диагоналях параллелограмма гласит, что точкой пересечения они делятся ровно пополовине.

По условию задачи O — это точка пересечения диагоналей AC и BD параллелограмма. AB эквивалентно BC, как противоположные, не имеющие своей общей вершины. CAD равен ACB также BDA и DBC, АD и BC секущими AC и B. D. Следуя дальше ∆АОD = ∆ COB, по стороне и двух прилегающих углах. Тогда, А = ОС, ВО = ОD, как соответствующие стороны разных треугольников.

На этом рисунке MN — это высота. Следуя за известным определением, из каждой вершины можно провести две высоты (BF и BT, которые приведены в соответствии к сторонам AD и CD).

Свойства параллелограмма с доказательствами 8 класса :

Две стороны равны и параллельны.
Противоположные стороны попарно равны.
Диагонали пересекаются и этой точкой делятся ровно пополам.
Противоположные углы попарно равны.

Теперь нужно вернуться к первому рисунку, чтобы до конца понять все признаки параллелограмма и доказательства любых признаков.

В нём AD = BC и AD || BC. Провели диагональ AC и получили ∆CAD и ∆ACB. CAD эквивалентен ВСА, как внутренние разносторонние углы при пересечениях прямых AD и BC секущей AC, ещё она является их общей стороной. Условия задачи говорят: AD=BC. Значит, что, ∆CAD=∆ACB, ACD = CAB. Из-за того, что они были созданы в таких условиях AB || CD, по признаку параллельных прямых.

Параллелограммы в геометрических построениях

Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны между собой.

Параллелограммы широко используются в геометрических построениях. Они позволяют строить различные фигуры и определять их свойства.

Построение прямоугольника

Прямоугольник – это частный случай параллелограмма, у которого все углы прямые. Для построения прямоугольника на плоскости необходимо знать длину двух сторон.

Нарисуйте отрезок AB с заданной длиной.
Из точки B проведите прямую, параллельную AB, с помощью линейки и ластика.
Из точки A постройте перпендикуляр к прямой, проведенной через B.
Продолжите отрезок AB до точки C, одной из точек пересечения прямой и перпендикуляра.
Проведите прямую, параллельную BC, из точки C с помощью линейки и ластика.
Из точки B постройте перпендикуляр к прямой, проведенной через C.
Продолжите отрезок BC до точки D, одной из точек пересечения прямой и перпендикуляра.

ABCD – прямоугольник.

Построение ромба

Ромб – это частный случай параллелограмма, у которого все стороны равны между собой. Для построения ромба необходимо знать длину одной стороны и один угол.

Нарисуйте отрезок AB с заданной длиной.
На отрезке AB откладывайте участки AC и AD, равные заданной длине.
При помощи транспортира проведите две прямые, образующие заданный угол, из точек C и D.
Из точек C и D постройте перпендикуляры к прямым, проведенным через A.
Продолжите отрезки AC и AD до точек E и F, одних из точек пересечения перпендикуляров и противоположных сторон AB.
Проведите прямую, параллельную BC, из точки E.
Из точки E постройте перпендикуляр к прямой, проведенной через B.
Продолжите отрезок BE до точки G, одной из точек пересечения прямой и перпендикуляра.

ABCDEG – ромб.

Построение квадрата

Квадрат – это частный случай прямоугольника и ромба, у которого все стороны равны между собой и все углы прямые. Для построения квадрата необходимо знать длину стороны.

Нарисуйте отрезок AB с заданной длиной.
Проведите перпендикулярные прямые из точек A и B.
Отметьте на прямых по две точки, равноудаленные от точки A и B соответственно.
Проведите прямую, проходящую через полученные точки.
Постройте перпендикуляр к этой прямой в точке A.
Продолжите отрезок AB до полученного перпендикуляра в точке C.
Постройте интересующий квадрат, используя отрезок AC в качестве одной из сторон.

ABCD – квадрат.

Формулы для углов

Если e, f, g и h отрезки касательных от вершин A, B, C и D соответственно к точкам касания окружности четырёхугольником ABCD, то углы четырёхугольника можно вычислить по формулам

sin⁡A2=efg+fgh+ghe+hef(e+f)(e+g)(e+h),{\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},}

sin⁡B2=efg+fgh+ghe+hef(f+e)(f+g)(f+h),{\displaystyle \sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(f+e)(f+g)(f+h)}}},}

sin⁡C2=efg+fgh+ghe+hef(g+e)(g+f)(g+h),{\displaystyle \sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}},}

sin⁡D2=efg+fgh+ghe+hef(h+e)(h+f)(h+g).{\displaystyle \sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}}.}

Угол между хордами KM и LN задаётся формулой(см. рисунок)

sin⁡φ=(e+f+g+h)(efg+fgh+ghe+hef)(e+f)(f+g)(g+h)(h+e).{\displaystyle \sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+h)(h+e)}}}.}

Сложные четырехугольники

антипараллелограмм

Самопересекающийся четырехугольник называется по-разному перекрестным четырехугольником , скрещенным четырехугольником , четырехугольником — бабочкой или четырехугольником с галстуком-бабочкой . В скрещенном четырехугольнике четыре «внутренних» угла по обе стороны от пересечения (два острых и два отраженных , все слева или все справа, как показано на рисунке) составляют в сумме 720 °.

(США) или трапеция (Содружество): скрещенный четырехугольник, в котором одна пара несмежных сторон параллельна (как у трапеции ) .
Антипараллелограмм : скрещенный четырехугольник, в котором каждая пара несмежных сторон имеет одинаковую длину (как параллелограмм ) .
Перекрещенный прямоугольник : антипараллелограмм, стороны которого являются двумя противоположными сторонами и двумя диагоналями прямоугольника , следовательно, имеет одну пару параллельных противоположных сторон.
: частный случай скрещенного прямоугольника, две стороны которого пересекаются под прямым углом.

Четырёхугольник — это… Что такое Четырёхугольник?

┌─────────────┼────────────┐
невыпуклый	выпуклый	самопересекающийся

┌─────────────┼─────────────┐

Вписанный	трапеция	описанный
\| ┌───────────┤	\|
равнобедренная трапеция равнобокая	параллелограмм стороны параллельны	выпуклый ромбоид (дельтоид) диагонали перпендикулярны
└─────┬─────┘	└─────┬─────┘
прямоугольник прямые углы	Ромб равнобедренный
└──────────┬─────────┘
квадрат

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники (см. рис.).

Виды четырёхугольников

Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
- Прямоугольник — четырёхугольник, у которого все углы прямые;
- Ромб — четырёхугольник, у которого все стороны равны;
- Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.

Четырёхсторонник

Хотя такое название может быть эквивалентно четырёхугольнику, в него часто вкладывают дополнительный смысл.

Четвёрка прямых, никакие две из которых не параллельны и никакие три не проходят через одну точку, называется четырёхсторонником.

Такая конфигурация встречается в некоторых утверждениях евклидовой геометрии (например, теорема Менелая, прямая Гаусса, прямая Обера и др.), в которых часто все прямые являются взаимозаменяемыми.

Свойства

Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
См. также свойства центроида четырёхугольника.
Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:

Его можно представить ещё в виде:

Площадь

Площадь произвольного четырёхугольника с диагоналями , и углом между ними (или их продолжениями), равна:
Площадь произвольного выпуклого четырёхугольника равна:

, где , — длины диагоналей, a, b, c, d — длины сторон.
, где p — полупериметр. Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.

История

В древности египтяне и некоторые другие народы использовали в качестве площади четырёхугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d: .

Документ без названия

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки.

Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла.

Четырехугольник, у которого угол больше развернутого называется невыпуклым

Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны; Прямоугольник — четырёхугольник, у которого все углы прямые; Ромб — четырёхугольник, у которого все стороны равны; Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны; Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
Свойства

Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.

Теорема Вариньона Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника. или сокращённо

Середины сторон произвольного четырёхугольника — вершины параллелограмма

Доказательство

Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников и . По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограм.

Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ проходит внутри четырёхугольника. Тогда площадь треугольника равна , где — высота треугольника , проведённая из вершины . Аналогично, площадь треугольника равна . Тогда площадь всего четырёхугольника равна . Но — это сумма расстояний до прямой от точек и , то есть в точности высота параллелограмма . А поскольку сторона параллелограмма вдвое меньше , то и площадь параллелограмма равна половине площади ,

Теорема Эйлера
в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Теорема Птолемея Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)

Если a, b, c, d – длины сторон четырёхугольника, – его полупериметр, а α – сумма его противоположных углов, то площадь Sчетырёхугольника равна . В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: ; это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: .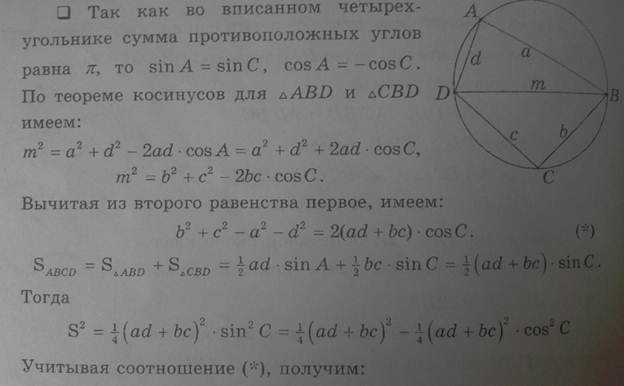

Виды трапеций

1. Трапеция
, у которой боковые стороны не равны,
называется разносторонней
(рис. 12).

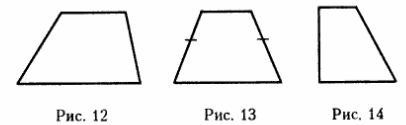
2. Трапеция, у которой боковые стороны равны, называется равнобокой
(рис. 13).

3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной
(рис. 14).

Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN
). Средняя линия трапеции параллельна основаниям и равна их полусумме.

Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).

Определение

Обобщённый четырёхугольник — это структура инцидентности (P,B, I), где I⊆P×B{\displaystyle \mathrm {I} \subseteq P\times B} — отношение инцидентности, удовлетворяющее определённым аксиомам. Элементы P по определению являются вершинами (точками) обобщённого четырёхугольника, элементы B — прямыми. Аксиомы следующие:

Существует число s (s ≥ 1), такое, что на любой прямой имеется в точности s + 1 точек. Существует максимум одна точка на двух различных прямых.
Существует число t (t ≥ 1), такое, что через любую точку проходит в точности t + 1 прямых. Существует максимум одна прямая через две различные точки.
Для любой точки p, не лежащей на прямой L, существует единственная прямая M и единственная точка q, такие, что p лежит на M, а q лежит на M и L.

Пара чисел (s,t) является параметрами обобщённого четырёхугольника. Параметры могут быть бесконечными. Если либо число s, либо t равно единице, обобщённый четырёхугольник называется тривиальным. Например, решётка 3×3 с P = {1,2,3,4,5,6,7,8,9} и B = {123, 456, 789, 147, 258, 369} является тривиальным обобщённым четырёхугольником с s = 2 и t = 1. Обобщённый четырёхугольник с параметрами (s,t) часто обозначается как GQ(s,t) (от английского Generalized Quadrangle).

Наименьший нетривиальный обобщённый четырёхугольник — GQ(2,2), представление которого в 1973 Стэн Пейн назвал «салфеткой».

Как описать четырехугольник окружностью?

Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.

Центр описанной окружности четырехугольника — это точка пересечения перпендикуляров, выходящих из середины сторон.

Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.

Найди ортодиагональные четырехугольники.

бимедианы

Параллелограмм Вариньона EFGH

Бимедианы — это отрезки, соединяющие середины противоположных сторон. Пересечение бимедиан является центром тяжести вершин четырехугольника.

Середины сторон любого четырехугольника (выпуклого, вогнутого или скрещенного) являются вершинами параллелограмма , называемого параллелограммом Вариньона . Он имеет следующие свойства:

Каждая пара противоположных сторон параллелограмма Вариньона параллельна диагонали исходного четырехугольника.
Сторона параллелограмма Вариньона вдвое меньше диагонали исходного четырехугольника, которому он параллелен.
Площадь параллелограмма Вариньона равна половине площади исходного четырехугольника. Это верно для выпуклых, вогнутых и скрещенных четырехугольников при условии, что площадь последнего определяется как разность площадей двух треугольников, из которых он состоит.
Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырехугольника.
Диагонали параллелограмма Вариньона являются бимедианами исходного четырехугольника.

Две бимедианы в четырехугольнике и отрезок, соединяющий середины диагоналей в этом четырехугольнике, совпадают и делятся пополам своей точкой пересечения.

В выпуклом четырехугольнике со сторонами a , b , c и d длина бимедианы, соединяющей середины сторон a и c , равна

мзнак равно12−а2+б2−с2+д2+п2+д2{\ displaystyle m = {\ tfrac {1} {2}} {\ sqrt {-a ^ {2} + b ^ {2} -c ^ {2} + d ^ {2} + p ^ {2} + д^{2}}}}

где p и q — длины диагоналей. Длина бимедианы, соединяющей середины сторон b и d , равна

нзнак равно12а2−б2+с2−д2+п2+д2.{\ displaystyle n = {\ tfrac {1} {2}} {\ sqrt {a ^ {2} -b ^ {2} + c ^ {2} -d ^ {2} + p ^ {2} + q ^{2}}}.}

Следовательно

п2+д2знак равно2(м2+н2).{\ displaystyle \ displaystyle p ^ {2} + q ^ {2} = 2 (m ^ {2} + n ^ {2}).}

Это также является следствием закона параллелограмма, примененного в параллелограмме Вариньона.

Длины бимедиан также могут быть выражены через две противоположные стороны и расстояние x между серединами диагоналей. Это возможно при использовании теоремы Эйлера о четырехугольнике в приведенных выше формулах. Откуда

мзнак равно122(б2+д2)−4Икс2{\ displaystyle m = {\ tfrac {1} {2}} {\ sqrt {2 (b ^ {2} + d ^ {2}) -4x ^ {2}}}}

нзнак равно122(а2+с2)−4Икс2.{\ displaystyle n = {\ tfrac {1} {2}} {\ sqrt {2 (a ^ {2} + c ^ {2}) -4x ^ {2}}}.}

Обратите внимание, что две противоположные стороны в этих формулах не являются двумя, которые соединяет бимедиана.

В выпуклом четырехугольнике существует следующая двойственная связь между бимедианами и диагоналями:

Две бимедианы имеют одинаковую длину тогда и только тогда , когда две диагонали перпендикулярны .
Две бимедианы перпендикулярны тогда и только тогда, когда две диагонали имеют одинаковую длину.

Косые четырехугольники

(Красные) боковые ребра тетрагонального дисфеноида представляют собой правильный зигзагообразный косой четырехугольник.

Неплоский четырехугольник называется косым четырехугольником . Формулы для вычисления его двугранных углов по длинам ребер и углу между двумя соседними ребрами были получены для работы над свойствами молекул, таких как циклобутан , которые содержат «морщинистое» кольцо из четырех атомов. Исторически термин « неопрятный четырехугольник » также использовался для обозначения косого четырехугольника. Косой четырехугольник вместе с его диагоналями образует (возможно, неправильный) тетраэдр и, наоборот, каждый косой четырехугольник исходит из тетраэдра, у которого удалена
пара противоположных ребер .

Замечательные точки и прямые в выпуклом четырехугольнике

Центр четырехугольника можно определить несколькими способами. «Центроид вершины» исходит из рассмотрения четырехугольника как пустого, но имеющего равные массы в вершинах. «Боковой центроид» исходит из того, что стороны имеют постоянную массу на единицу длины. Обычный центр, называемый просто центроидом (центром площади), возникает из-за того, что поверхность четырехугольника рассматривается как имеющая постоянную плотность. Эти три пункта в общем случае не являются одним и тем же пунктом.

«Центроид вершины» — это пересечение двух . Как и в случае любого многоугольника, координаты x и y центроида вершины являются средними арифметическими координат x и y вершин.

«Центроид площади» четырехугольника ABCD можно построить следующим образом. Пусть G _a , G _b , G _c , G _d — центроиды треугольников BCD , ACD , ABD , ABC соответственно. Тогда «центроид площади» является пересечением линий G _a G _c и G _b G _d .

В общем выпуклом четырехугольнике ABCD нет естественных аналогий центру описанной окружности и ортоцентру треугольника . Но две такие точки можно построить следующим образом. Пусть O _a , O _b , O _c , O _d — центры описанных окружностей треугольников BCD , ACD , ABD , ABC соответственно; и обозначим через H _a , H _b , H _c , H _d ортоцентры в тех же треугольниках. Тогда пересечение прямых O _a O _c и O _b O _d называется центром квазиокружности , а пересечение прямых H _a H _c и H _b H _d называется квазиортоцентром выпуклого четырехугольника. Эти точки можно использовать для определения линии Эйлера четырехугольника. В выпуклом четырехугольнике квазиортоцентр H , «центроид площади» G и квазицентр окружности O коллинеарны в этом порядке, и HG = 2 GO .

Также можно определить квазиневятиточечный центр E как пересечение прямых E _a E _c и E _b E _d , где E _a , E _b , E _c , E _d — центры девяти точек треугольников BCD , ACD , ABD , ABC соответственно. Тогда Е — середина ОН .
_

Еще одна замечательная линия в выпуклом четырехугольнике, не являющемся параллелограммом, — это линия Ньютона , которая соединяет середины диагоналей, причем отрезок, соединяющий эти точки, делится пополам центром тяжести вершины. Еще одна интересная линия (в некотором смысле двойственная ньютоновской ) — это линия, соединяющая точку пересечения диагоналей с центром тяжести вершины. Линия примечательна тем, что содержит центр тяжести (площади). Центроид вершины делит отрезок, соединяющий пересечение диагоналей и центроид (площадь) в отношении 3:1.

Для любого четырехугольника ABCD с точками P и Q пересечения AD и BC и AB и CD соответственно, окружности (PAB), (PCD), (QAD) и (QBC) проходят через общую точку M , называемую микелевой точка.

Для выпуклого четырехугольника ABCD , в котором E — точка пересечения диагоналей, а F — точка пересечения продолжений сторон BC и AD , пусть ω — окружность, проходящая через E и F , которая пересекает CB внутри в M и DA внутри . в Н. _ Пусть CA снова встречается с ω в точке L , а DB снова встречается с ω в точке K. Тогда верно: прямые NK и ML пересекаются в точке P , лежащей на стороне AB ; прямые NL и KM пересекаются в точке Q , расположенной на стороне CD . Точки P и Q называются «точками Паскаля», образованными окружностью ω на сторонах AB и CD .

Свойства четырёх внутренних треугольников

Описание Чао и Симеонова (Chao, Simeonov) в терминах радиусов окружностей, вписанных в каждый из четырёх и треугольников

Для непересекающихся треугольниках APB, BPC, CPD, DPA, образованных диагоналями выпуклого четырёхугольника ABCD, где диагонали пересекаются в точке P, имеются следующие свойства.

Пусть r₁, r₂, r₃ и r₄ означают радиусы вписанных окружностей треугольников APB, BPC, CPD и DPA соответственно. Чао и Симеонов доказали, что четырёхугольник является описанным тогда и только тогда, когда

1r1+1r3=1r2+1r4.{\displaystyle {\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{4}}}.}

Это свойство было доказано пятью годами ранее Вайнштейном.
В решении его задачи похожее свойство было дано Васильевым и Сендеровым. Если через h_M, h_K, h_N и h_L обозначить высоты тех же треугольников (опущенных из пересечения диагоналей P), то четырёхугольник является описанным тогда и только тогда, когда

1hM+1hN=1hK+1hL.{\displaystyle {\frac {1}{h_{M}}}+{\frac {1}{h_{N}}}={\frac {1}{h_{K}}}+{\frac {1}{h_{L}}}.}

Ещё одно похожее свойство относится к радиусам вневписанных окружностей r_M, r_K, r_N и r_L для тех же четырёх треугольников (четыре вневписанные окружности касаются каждой из сторон четырёхугольника и продолжений диагоналей). Четырёхугольник является описанным в том и только в том случае, когда

1rM+1rN=1rK+1rL.{\displaystyle {\frac {1}{r_{M}}}+{\frac {1}{r_{N}}}={\frac {1}{r_{K}}}+{\frac {1}{r_{L}}}.}

Если R_M, R_K, R_N и R_L — радиусы описанных окружностей треугольников APB, BPC, CPD и DPA соответственно, то треугольник ABCD является описанным тогда и только тогда, когда

RM+RN=RK+RL.{\displaystyle R_{M}+R_{N}=R_{K}+R_{L}.}

В 1996 Вайнштейн, похоже, был первым, кто доказал ещё одно замечательное свойство описанных четырёхугольников, которое позднее появилось в нескольких журналах и сайтах. Свойство утверждает, что если выпуклый четырёхугольников разделён на четыре неперекрывающихся треугольника его диагоналями, центры вписанных окружностей этих треугольников лежат на одной окружности тогда и только тогда, когда четырёхугольник является описанным. Фактически центры вписанных окружностей образуют ортодиагональный вписанный четырёхугоольник . Здесь вписанные окружности можно заменить на вневписанные (касающиеся стороны и продолжения диагоналей четырёхугольника). Тогда выпуклый четырёхугольник является описанным тогда и только тогда, когда центры вневписанных окружностей являются вершинами вписанного четырёхугольника.

Выпуклый четырёхугольник ABCD, в котором диагонали пересекаются в точке P, является описанным тогда и только тогда, когда четыре центра вневписанных окружностей треугольников APB, BPC, CPD и DPA лежат на одной окружности (здесь вневписанные окружности пересекают стороны четырёхугольника, в отличие от аналогичного утверждения выше, где вневписанные окружности лежат вне четырёхугольника). Если R_m, R_n, R_k и R_l — радиусы вневписанных окружностей APB, BPC, CPD и DPA соответственно, противоположных вершинам B и D, то ещё одним необходимым и достаточным условием того, что четырёхугольник является описанным, будет

1Rm+1Rn=1Rk+1Rl.{\displaystyle {\frac {1}{R_{m}}}+{\frac {1}{R_{n}}}={\frac {1}{R_{k}}}+{\frac {1}{R_{l}}}.}

Далее выпуклый четырёхугольник, в котором диагонали пересекаются в точке P, является описанным тогда и только тогда, когда

m△(APB)+n△(CPD)=k△(BPC)+l△(DPA){\displaystyle {\frac {m}{\triangle (APB)}}+{\frac {n}{\triangle (CPD)}}={\frac {k}{\triangle (BPC)}}+{\frac {l}{\triangle (DPA)}}}

где m, k, n, l – длины сторон AB, BC, CD и DA, а ∆(APB) — площадь треугольника APB.

Обозначим отрезки, на которые точка P делит диагональ AC как AP = p_a и PC = p_c. Аналогичным образом P делить диагональ BD на отрезки BP = p_b и PD = p_d. Тогда четырёхугольник является описанным тогда и только тогда, когда выполняется одно из равенств:

mpcpd+npaqb=kpapd+lpcpb{\displaystyle mp_{c}p_{d}+np_{a}q_{b}=kp_{a}p_{d}+lp_{c}p_{b}}

или

(pa+pb−m)(pc+pd−n)(pa+pb+m)(pc+pd+n)=(pc+pb−k)(pa+pd−l)(pc+pb+k)(pa+pd+l){\displaystyle {\frac {(p_{a}+p_{b}-m)(p_{c}+p_{d}-n)}{(p_{a}+p_{b}+m)(p_{c}+p_{d}+n)}}={\frac {(p_{c}+p_{b}-k)(p_{a}+p_{d}-l)}{(p_{c}+p_{b}+k)(p_{a}+p_{d}+l)}}}

или

(m+pa−pb)(n+pc−pd)(m−pa+pb)(n−pc+pd)=(k+pc−pb)(l+pa−pd)(k−pc+pb)(l−pa+pd).{\displaystyle {\frac {(m+p_{a}-p_{b})(n+p_{c}-p_{d})}{(m-p_{a}+p_{b})(n-p_{c}+p_{d})}}={\frac {(k+p_{c}-p_{b})(l+p_{a}-p_{d})}{(k-p_{c}+p_{b})(l-p_{a}+p_{d})}}.}

Классификация треугольников

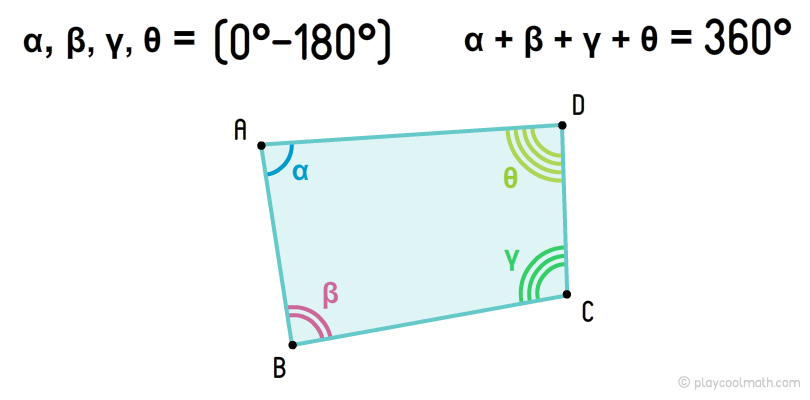
Выпуклые четырехугольники

Выпуклый четырехугольник — это четырехугольник, у которого все углы выпуклые (от 0° до 180°, не включая эти значения). Сумма всех углов выпуклого четырехугольника всегда равна 360°

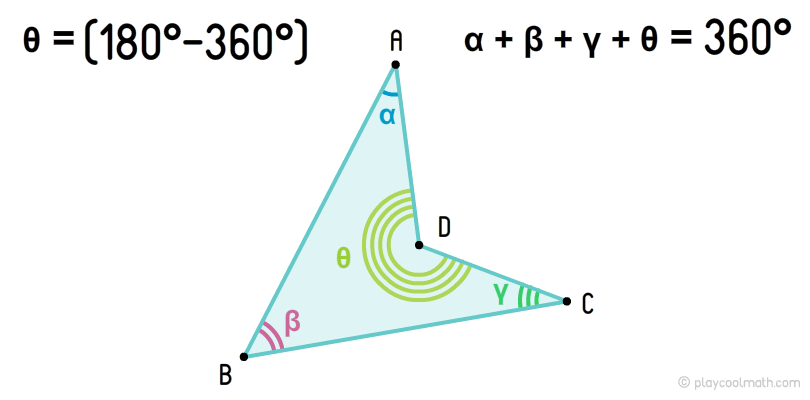
Невыпуклые или вогнутые четырехугольники

Вогнутый четырехугольник — это четырехугольник, у которого один угол вогнутый (от 180° до 360°, не включая эти значения). Сумма всех углов вогнутого четырехугольника всегда равна 360°

Самопересекающиеся четырехугольники

Самопересекающийся четырехугольник — это четырехугольник, у которого противоположные стороны пересекаются.

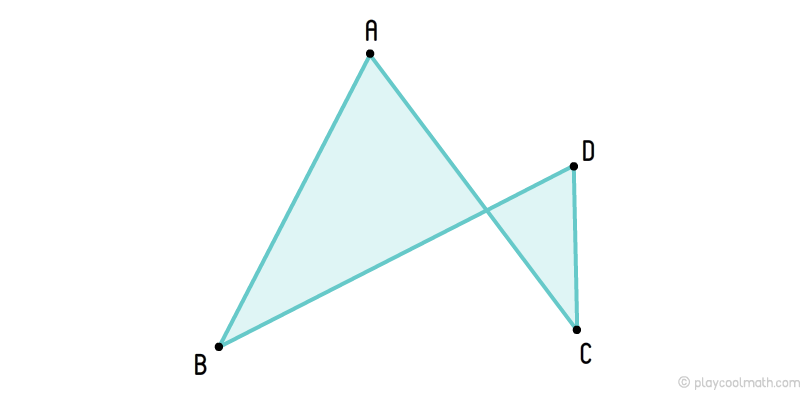
Визуально самопересекающийся четырехугольник похож на два треугольника у которых стороны лежать на двух пересекающихся линиях, а точка пересечения это общая вершина для треугольников.