Радиус цилиндра, онлайн расчет

Вычисление объема тел вращения

Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

Рассмотрим, как на практике используется эта формула.

Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

Широкое применение цилиндров в повседневной жизни

Цилиндр — это геометрическое тело, которое может использоваться в различных областях. Ниже приведены некоторые примеры использования цилиндра:

Создание двигателей внутреннего сгорания: таких как двигатель автомобиля или мотоцикла.
Механика: например в гидравлических цилиндрах, которые используются для перемещения или прессования тяжелых предметов.
Создание емкостей: таких как баки для хранения газа или жидкости.
Столярное дело: для создания столбов, колонн или других элементов архитектуры.
Математика: для решения геометрических задач и для вычисления объемов и площадей тел.
Кулинария: для формирования булочек, пирогов, кексов и других блюд.
Сосуды для хранения и транспортировки жидкостей: таких как газы, масла, смазки и прочее.
Научные исследования: например для измерения давления, температуры и других параметров.

Вопросы и ответы

Обратите внимание на ответы на некоторые часто задаваемые вопросы

Какова формула для вычисления площади цилиндра?

Формула для вычисления площади цилиндра зависит от того, какую площадь вы хотите найти. Обычно вычисляют площадь боковой поверхности и площадь полной поверхности цилиндра. Для нахождения площади боковой поверхности цилиндра используйте формулу 2πrh, где r — радиус цилиндра, а h — его высота. Для нахождения площади полной поверхности цилиндра нужно прибавить к площади боковой поверхности удвоенную площадь оснований, т.е. используйте формулу 2πrh + 2πr^2.

Как использовать онлайн калькулятор для вычисления площади цилиндра?

Чтобы использовать онлайн калькулятор для вычисления площади цилиндра, вам нужно ввести значения радиуса и высоты цилиндра в соответствующие поля. Затем онлайн калькулятор автоматически рассчитает площадь цилиндра.

Как найти радиус цилиндра, если известна его площадь?

Для нахождения радиуса цилиндра по известной площади необходимо использовать формулу S = 2πrh + 2πr^2, где S — площадь цилиндра, r — радиус цилиндра, h — его высота. После подстановки известных значений в формулу можно найти радиус цилиндра.

Результаты вычислений, полученные с помощью онлайн калькулятора площади цилиндра, можно использовать для решения различных задач, связанных с геометрией, например, для расчета объема цилиндра, для определения необходимого количества материала для изготовления цилиндрического объекта или для определения количества жидкости, которая может поместиться в цилиндрический резервуар.

Как рассчитать диаметр шара по его радиусу

Диаметр шара – это расстояние между двумя точками на противоположных концах его. Он равен удвоенному радиусу, то есть d = 2r.

Чтобы рассчитать диаметр шара по его радиусу, нужно умножить радиус на 2. Например, если радиус шара равен 5 см, его диаметр будет равен 10 см (d = 2 × r = 2 × 5 см = 10 см).

Эта формула полезна в различных математических задачах, где необходимо знать диаметр шара по его радиусу, или наоборот. Она также может быть использована при расчете объема шара, который можно вычислить по формуле V = 4/3 × π × r³ (где π ≈ 3,14).

Важно помнить, что диаметр шара всегда будет больше его радиуса. Кроме того, данная формула применима только к шарам – для расчета диаметра других геометрических фигур требуются другие формулы

Площадь сферы

В предыдущих уроках мы уже узнали формулу для вычисления площади сферы, однако тогда мы ее не доказывали. Однако теперь мы можем ее доказать, используя формулу объема шара. Но сначала напомним саму формулу:

Впишем сферу в многогранник с n гранями. Ясно, что расстояние от граней этого многогранника до центра сферы равно радиусы сферы R. Далее построим пирамиды, чьи вершины находятся в центре сферы, а основания – это грани многогранника. Заметим, что такие пирамиды будут иметь одинаковые высоты длиной R.

Обозначим площади граней многогранника как S₁, S₂, S₃,…S_n. Тогда объемы пирамид, построенных на этих гранях, вычисляются так:

Заметим, что в сумме эти объемы дают объем всего многогранника, а сумма площадей S₁, S₂, S₃,…S_n – это площадь всей его поверхности. Тогда можно записать:

Теперь начнем неограниченно уменьшать размеры граней многогранника. Тогда число n будет расти, объем многогранника будет приближаться к объему шара, а площадь многогранника – к площади к сфере. Тогда и доказанное равенство можно будет записать так:

Задание. Необходимо изготовить закрытый сосуд с заранее заданным объемом V. Предлагается два варианта формы этого сосуда – шар и куб. Так как поверхность сосуда покрывается очень дорогой краской, то необходимо выбрать вариант с меньшей площадью поверхности. Какую форму для сосуда следует выбрать?

Решение. Обозначим радиус шара как R, а ребро куба как а. Тогда можно записать:

Теперь надо выяснить, какое из полученных значений больше. Для этого поделим площадь куба на площадь сферы. Если получится число, большее единицы, то площадь куба больше:

Получившееся число больше единицы, ведь 6 больше числа π, равного 3,1415926… Значит, и площадь куба больше, а потому необходимо выбрать сосуд, имеющий форму шара.

Ответ: шар.

Примечание. Более сложными математическими методами можно доказать, что если второй сосуд имеет не форму куба, а вообще любую форму, отличную от шара, то всё равно следует выбирать именно сосуд в форме шара. То есть из всех поверхностей, ограничивающих определенный объем, именно сфера имеет наименьшую площадь. Этот факт имеет и физическое следствие – капли дождя и мыльные пузыри стремятся принять форму шара, также как и любые жидкости, находящиеся в невесомости.

Итак, мы научились вычислять объемы таких тел, как конус, пирамида, шар, призма. Также помощью интегрирования можно находить объемы и ещё более сложных тел, если мы можем составить функцию, описывающую площадь их сечения.

❓ Вопросы и ответы

Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.

Что такое цилиндр?

Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.

Как вычислить объем цилиндра?

Объем цилиндра можно вычислить, используя формулу:

V = πr²h

где V — объем цилиндра, π — число Пи (приблизительно равно 3.14), r — радиус основания цилиндра и h — высота цилиндра.

Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?

Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.

Как найти радиус или диаметр цилиндра, если они неизвестны?

Если известна площадь основания цилиндра, можно найти радиус, используя формулу:

r = √(A/π)

где A — площадь основания цилиндра.

Если известен объем цилиндра, можно найти радиус, используя формулу:

r = √(V/πh)

где V — объем цилиндра, h — высота цилиндра.

Диаметр можно найти, удваивая радиус.

Как найти объем трубы или канала?

Для трубы или канала формула для вычисления объема имеет немного другой вид:

V = πr²h

где V — объем, r — радиус, h — длина (высота) трубы или канала.

Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:

V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.

Как узнать, сколько литров вмещает бочка?

Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота — 1,5 метра, то ее объем будет:

V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.

Как узнать, сколько литров вмещает труба?

Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы — 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:

V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.

Какой тип калькулятора нужен для расчета объема цилиндра?

Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.

Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?

Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.

Как рассчитать объем цилиндра по площади его основания и высоте

Формула расчета объема цилиндра:

Объем цилиндра можно рассчитать по формуле: V = S * h, где S — площадь основания цилиндра, h — его высота.

Для расчета объема цилиндра необходимо знать площадь основания и высоту. Площадь основания можно найти по формуле, соответствующей его форме. Например, для круглого основания, S = π * r^2, где r — радиус круга.

После нахождения площади основания и высоты цилиндра, можно просто перемножить их, чтобы получить объем цилиндра.

Пример расчета объема цилиндра:

Допустим, у нас есть цилиндр высотой 10 см и радиусом основания 5 см.

Сначала необходимо найти площадь его основания по формуле S = π * r^2: S = 3.14 * 5^2 = 78.5 см^2.

Затем, перемножим площадь и высоту: V = S * h = 78.5 см^2 * 10 см = 785 см^3.

Таким образом, объем цилиндра равен 785 см^3.

Как вычислить объем круглой емкости

Инструкция для калькулятора количества и объема жидкости в цистерне

Размеры вводите в миллиметрах:

D – диаметр емкости можно замерить рулеткой. Необходимо помнить что диаметр – это отрезок наибольшей длины, соединяющий две точки на окружности и проходящий через ее центр.

H – уровень жидкости замеряют, используя метршток, но если такого инструмента нет под рукой, воспользуйтесь обычным стержнем из проволоки или деревянной планкой подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в цистерну до дна, отметьте на нем уровень, достаньте и измерьте рулеткой. Также определить H можно, измерив, расстояние от верха цистерны до поверхности жидкости и отняв этот показатель от значения диаметра.

L – длина емкости.

Если необходим чертеж в бумажном виде, целесообразно отметить пункт «Черно-белый чертеж». Вы получите контрастное изображение и сможете его распечатать, не расходуя зря цветную краску или тонер.

Нажмите «Рассчитать» и получите следующие данные:

Объём емкости – этот параметр характеризует полный объём цистерны, т.е. какое максимальное количество жидкости в кубических метрах или литрах может в нее поместиться.

Количество жидкости – сколько вещества находится в цистерне на данный момент.

Свободный объём позволяет оценить, сколько жидкости еще можно залить в емкость.

В результате, Вы получаете расчет не только объема цистерны, но и объема жидкости в неполной цистерне.

Изделия из металла следует периодически красить, тогда срок их службы значительно возрастет. Зная площадь передней поверхности, площадь боковой поверхности и общую площадь емкости легко оценить необходимое количество лакокрасочных материалов для обработки всей емкости или ее отдельных частей.

Перевести кубы в литры и обратно

Литр (обозначение — л; L или l) — внесистемная метрическая единица измерения объёма и вместимости, равная 1 кубическому дециметру.

— Название литр идет французской единицы «литрон». Она использовалась для измерения сыпучих веществ. Его величина была меньше, чем современный литр и составляла около 830 грамм. Название «литрон» берет свое начало от монеты того времени – ЛИТРА, которая имела соответствующий вес – около 830 грамм.

— В 1901 году принято определение литра: объем, занимающий 1 кг воды, при температуре воды +3,98 градусов по Цельсию и 1 единице атмосферного давления.

— Литр не считается единицей СИ. Единица объема СИ – кубический метр.

Сколько литров в кубическом метре

Кубический метр (русское обозначение: куб. м. (м³); международное: cu m (m³)) — термин и его сокращения образованы от слов куб и метр. В метрической системе мер: 1 м³ = 1000 дм³ = 1 000 000 см³ = 1 000 000 000 мм³ = 1000 литров.

Как рассчитать объем кастрюли в литрах, формула

Чтобы рассчитать объем кастрюли в литрах необходимо измерить диаметры и высоту емкости.

В зависимости от формы кастрюли, диаметры могут отличаться.

Желательно снимать размеры изнутри, чтобы убрать из расчета толщину стенок. И как было сказано выше, высоту кастрюли замеряют под прямым углом к ее основанию.

Далее, полученные значения необходимо подставить в формулу:

Объем кастрюли = ( 1/3 * Пи * h * ( (D/2)² + ((D/2) * (d/2) ) + (d/2)² ) ) / 1000

Обратите внимание — значения подставляют в формулу в единой мере измерения, в нашем случае — это сантиметры

1 куб воды сколько литров? | ТАБЛИЦА

Число кубовЛитров (л)Дециметров (дм³)

1	1000	1000
2	2000	2000
3	3000	3000
4	4000	4000
5	5000	5000
6	6000	6000
7	7000	7000
8	8000	8000
9	9000	9000
10	10000	10000

Далее можете проводит расчет сами по формуле:

A – число кубов,
1000 – литров в 1 кубе.

Цилиндр, его элементы и виды цилиндров

Наиболее распространенным видом цилиндра в геометрии является прямой круговой цилиндр. Введем его определение.

По определению понятно, почему в некоторых случаях эту фигуру называют цилиндром вращения.

На рисунке выше изображен цилиндр, который является результатом вращения прямоугольника АВСD вокруг оси, обозначенной О1О2. Поворот происходит на 180°. Аналогичный итог получаем, если повернуть ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.

Перечислим ключевые элементы цилиндра:

Основания цилиндра в виде пары идентичных по габаритам и площади круга с центральными точками, обозначенными за О1 и О2.
R определяет радиус, который имеют основания геометрической фигуры.
AD и BC являются диаметрами (d) оснований цилиндра.
O1O2 представляет собой ось симметрии рассматриваемого цилиндра, а также играет роль его высоты (h).
l (AB, CD) в виде образующих цилиндра являются сторонами прямоугольника ABCD, которые соответствуют высоте геометрической фигуры.

Представим изображение развертки цилиндра:

Заметим справедливость следующих соотношений:

рассматриваемый прямоугольник имеет длину, равную длине окружности основания цилиндра ;
ширина соответствует высоте (образующей) цилиндра.

Геометрическая фигура в виде цилиндра может обладать следующими видами сечений:

1. Осевое сечение имеет прямоугольную форму, сформировано при пересечении цилиндра плоскостью, которая пролегает через ее ось. На примере первого рисунка осевым сечением является АВСD. Определить площадь данного сечения легко, достаточно умножить высоту цилиндра на диаметр его основания.

2. Сечение в виде прямоугольника образуется в том случае, когда секущая плоскость не пересекает ось фигуры, но расположена перпендикулярно по отношению к основаниям цилиндра.

3. Сечение в виде аналогичного основаниям цилиндра круга образовано при условии параллельности секущей плоскости основаниям рассматриваемой фигуры.

4. При пересечении цилиндра плоскостью, которая не является параллельной его основаниям и не пересекается с ними, образуется сечение в виде эллипса.

5. Сечение в виде параболы и гиперболы сформировано путем пересечения секущей плоскости с одним из оснований цилиндра.

Рассмотрим основные виды цилиндров с примерами, которые часто встречаются на уроках в классе. Сначала разберемся с понятием прямого цилиндра.

Данная фигура обладает идентичными основаниями, расположенными симметрично и параллельно, в виде круга или эллипса. Отрезок, соединяющий точки симметрии оснований, является перпендикуляром к этим основаниям, осью симметрии и равен высоте фигуры.

Наклонный цилиндр обладает идентичными основаниями, которые расположены параллельно относительно друг друга. Отрезок, соединяющий точки симметрии, не перпендикулярен к основаниям фигуры.

Косой, или скошенный, цилиндр отличается расположением оснований. В данном случае они расположены не параллельно друг другу.

В круговом цилиндре основания имеют форму кругов.

Существуют также такие разновидности цилиндров:

эллиптические;
параболические;
гиперболические.

Равносторонний цилиндр представляет собой прямой круговой цилиндр с основанием, диаметр которого соответствует высоте фигуры.

Как рассчитать объем шара по его радиусу

Формула для расчета объема шара

Для расчета объема шара необходимо знать его радиус. Объем шара можно вычислить по формуле:

V = (4/3) * π * r^3

где V — объем шара, r — радиус шара, π — математическая константа (3,14).

Пример расчета объема шара

Предположим, что радиус шара равен 5 см. Тогда, можно рассчитать его объем по формуле:

V = (4/3) * π * 5^3 ≈ 523,6 см³

Таким образом, объем шара с радиусом 5 см будет примерно равен 523,6 кубическим сантиметрам.

Как использовать расчет объема шара?

Расчет объема шара может пригодиться при различных задачах, таких как расчет объема шарообразной бочки или определение объема своей головы

Также, зная объем шара, можно рассчитать его массу или плотность, что может пригодиться при решении различных задач в физике или химии.

Занимательные факты

Это интересно:

У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.

Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.

Применение формулы

Рассмотрим на примере, как вычислить площадь круглого шара
, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.

Формула вычисления площади
применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.

Формула вычисления объёма
может пригодиться и строительной бригаде, что делает ремонт

И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике

Но как быть, если не представляется возможным измерить объект?
Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.

Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара,
был Архимед
. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.

Именно Архимед определил границы числа «пи»
и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.

Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; вычисляется как произведение числа π высоты фигуры на квадрат радиуса окружности, являющейся ее основанием.

V = πR2h

R — радиус основания цилиндра, т.е окружностей;
π — это число, округленное значение которого равно 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра рассчитывается следующим образом:

Сторона – площадь боковой поверхности цилиндра; равен произведению длины окружности (2πR), являющейся основанием фигуры, на ее высоту:

S = 2πRh

3. Через полную площадь поверхности

Радиус цилиндра равен:

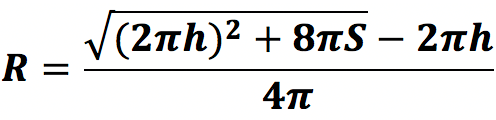
Эта формула выводится следующим образом:

S – общая площадь поверхности фигуры, равная:

S = 2πRh + 2πR2 или S = 2πR(h + R)

Возьмем первое выражение. Если мы переместим S в правую сторону, мы получим:

2πR2 + 2πRh – S = 0

Вы можете видеть, что это квадратное уравнение вида ax2 + bx + c = 0, где:

а = 2π
б = 2πt
с=-S

R является корнем данного уравнения (x). Подставив наши значения a, b и ci в стандартную формулу вычисления корней, получим*:

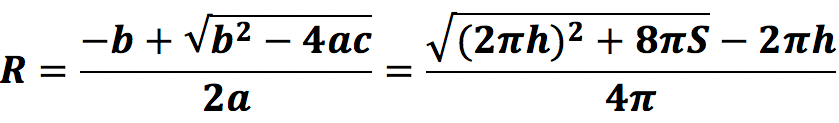
* в нашем случае — только положительный корень, потому что радиус не может быть отрицательным.

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:

А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:

Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.

Формула площади осевого сечения цилиндра выводится из формулы расчета :

Существует большое количество задач, связанных с цилиндром. В них нужно находить радиус и высоту тела или вид его сечения. Плюс ко всему, иногда требуется вычислить площадь цилиндра и его объем.

Радиус цилиндра.

Отзыв от Bogna Szyk и Adena Benn

Последнее обновление: 20 ноября 2022 г.

Какова формула радиуса цилиндра?
Как найти радиус цилиндра?
Часто задаваемые вопросы

Этот калькулятор радиуса цилиндра быстро находит радиус правильного кругового цилиндра с восемью различными уравнениями . Вам нужно решить конкретную математическую задачу, но вы не знаете, как найти радиус цилиндра? Попробуйте ввести пару параметров и посмотрите, как просто работает этот калькулятор.

Существует множество различных способов оценки радиуса цилиндра. В следующем тексте мы представили восемь формул радиуса цилиндра, которые используются нашим калькулятором. В большинстве случаев вам понадобятся только два из следующих количеств:

высота ;
том ;
самая длинная диагональ ;
площадь основания ;
площадь боковой поверхности ;
общая площадь поверхности ; или
отношение поверхности к объему .

Этот калькулятор радиуса цилиндра является удобным инструментом, который может вычислить параметры правильных круговых цилиндров . Под радиусом цилиндра мы понимаем радиус двух конгруэнтных окружностей, равных базы цилиндра. Вот почему этот тип цилиндра называется круговым .

Следует помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр). Однако обычно мы имеем в виду правильный круговой цилиндр. Цилиндр прямо , когда одно из оснований лежит точно над другим. В противном случае цилиндр косой .

Этот калькулятор был подготовлен для ответа на вопрос как найти радиус цилиндра . В другом нашем правом расчете цилиндров вы можете найти более общую информацию о цилиндрах. Обязательно проверьте это!

Какова формула радиуса цилиндра?

Для описания свойств цилиндра мы обычно используем радиус и высоту .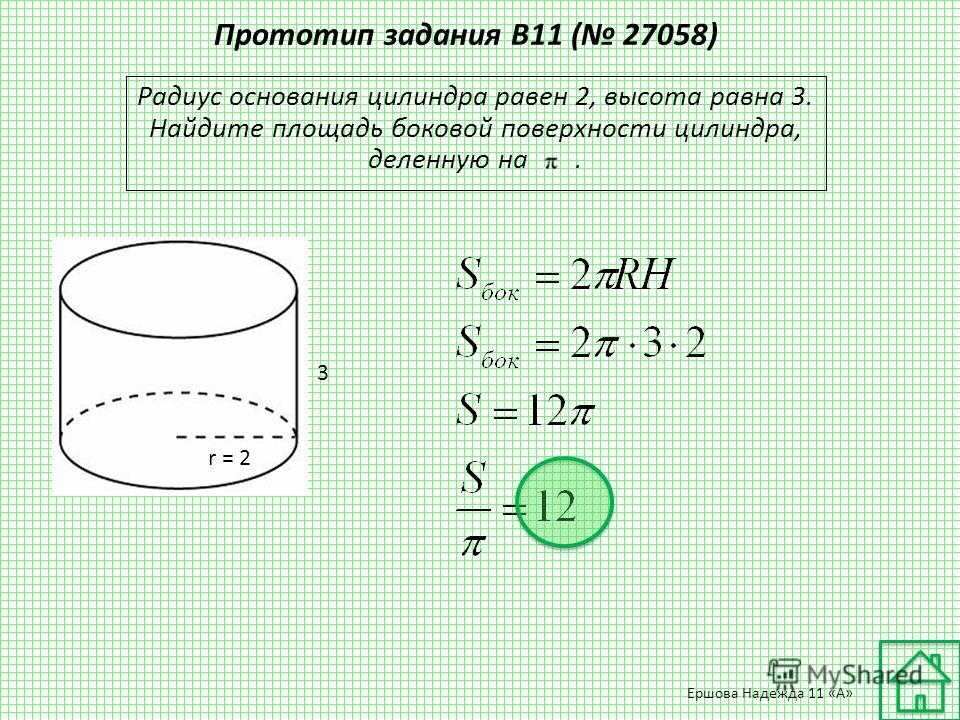

Объем цилиндра: ,
Площадь основания цилиндра: ,
Площадь боковой поверхности цилиндра: ,
Общая площадь поверхности цилиндра: ,
Наибольшая диагональ цилиндра: ,
Отношение площади поверхности к объему цилиндра:

Радиус цилиндра не всегда легко оценить. Однако с нашим калькулятором радиуса цилиндра теперь вы можете быстро вычислить его с помощью следующих формул восьми радиусов цилиндра . Все они были получены непосредственно из приведенных выше уравнений.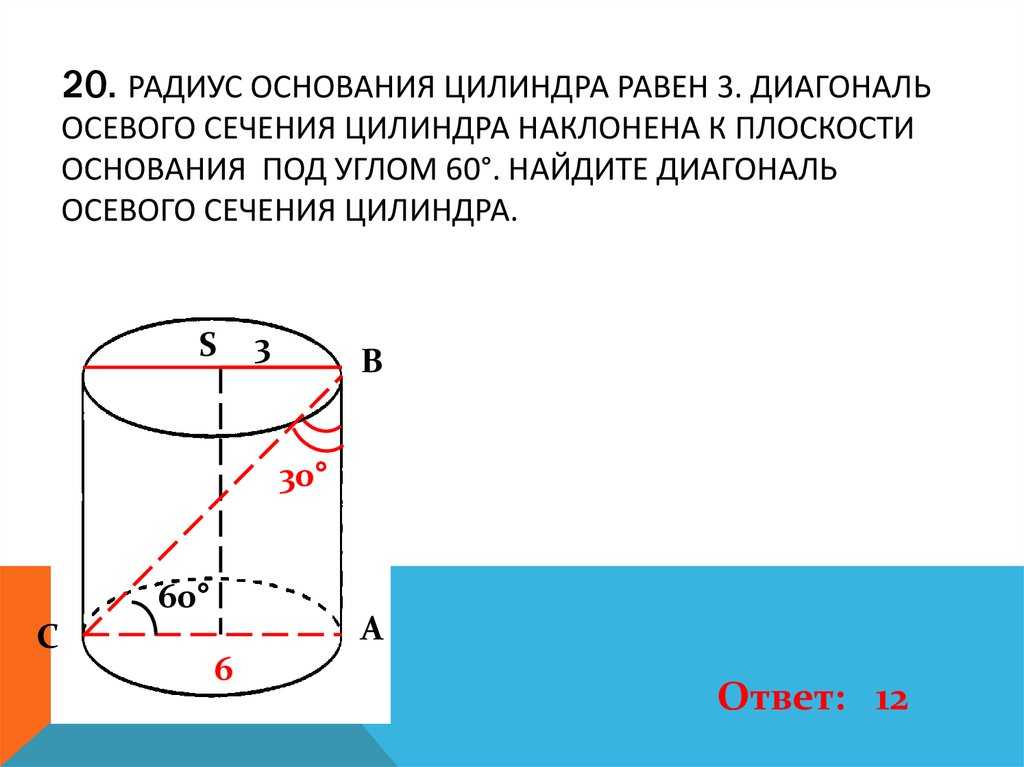

Учитывая высоту и объем : ;
Учитывая высоту и боковую площадь : ;
Учитывая высоту и общую площадь : ;
Учитывая высоту и диагональ : ;
Учитывая высоту и отношение площади поверхности к объему : ;
Учитывая объем и боковую площадь : ;
Учитывая базовую площадь : ; и
Учитывая боковой площади и общей площади : .

Вам нужно рассчитать еще один параметр цилиндра? Вам обязательно нужно проверить наш калькулятор площади поверхности цилиндра и калькулятор высоты цилиндра!

Как найти радиус цилиндра?

Калькулятор радиуса цилиндра является полезным инструментом, предназначенным для решения широкого круга различных задач.

Определите какие параметры цилиндра вам известны.
Введите значений выбранных величин.
Считать результат вычислений.

Разве это не просто? Кроме того, с помощью нашего калькулятора вы можете выбрать единицы измерения любого параметра, который вам нужен. Это может быть очень полезно во многих вычислениях! Если вы хотите узнать больше о преобразовании единиц измерения, обязательно ознакомьтесь с преобразователем длины и инструментом преобразования объема!

Объем пирамиды

Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

Объем треугольных пирамид рассчитывается по выведенной нами формуле:

Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований: