Решение матриц — методы вычисления с примерами

Нахождение определителя матрицы

Определитель матрицы обозначается как $Δ$ или $\det$.

Замечание 2

Детерминант возможно найти только для квадратных разновидностей матриц.

В простейшем случае, когда матрица состоит из всего одного элемента, её определитель равен этому элементу:
$det A = |a_{11}|= a_{11}$

Вычислить определитель от матрицы порядка двух можно следуя такому правилу:

Определение 1

Определитель матрицы размера 2 равен разности произведений элементов, стоящих на главной диагонали с произведением элементов с побочной диагонали:

$\begin{array}{|cc|} a_{11}& a_{12} \\ a_{21} & a_{22} \\ \end{array} = a_{11} \cdot a_{22} – a_{12} \cdot a_{21}$

В случае если определитель матрицы задан размером $3 \times 3$, то найти его можно используя мнемонические правила: Саррюса или треугольников, также можно разложить матрицу по строчке или столбцу или воспользоваться преобразованиями Гаусса.

Для определителей большего размера можно использовать преобразования Гаусса и разложение по строчке.

Теория Матриц и Определителей

Средняя школа № 45.

Город Москва.

Ученик 10 класса “Б” Горохов Евгений

Курсовая работа (черновик).

Введение в теорию матриц и
определителей.

1996 год.

Оглавление.

Оглавление……………………………………………………………………………………………………………………………………..

1. Матрицы………………………………………………………………………………………………………………………………………..

1.1 Понятие матрицы……………………………………………………………………………………………………………………

1.2 Оновные операции над матрицами……………………………………………………………………………………

2. Определители……………………………………………………………………………………………………………………………..

2.1 Понятие определителя…………………………………………………………………………………………………………..

2.2 Вычисление определителей………………………………………………………………………………………………….

2.3 Основные свойства определителей……………………………………………………………………………………

3. Системы линейных уравнений…………………………………………………………………………………………

3.1 Основные определения…………………………………………………………………………………………………………..

3.2 Условие совместности систем линейных уравнений…………………………………………………..

3.3 Решение ситем линейных уравнений метедом Крамера……………………………………………..

3.4 Решение ситем линейных уравнений метедом Гаусса………………………………………………..

4. Обратная матрица…………………………………………………………………………………………………………………..

4.1 Понятие обратной матрицы…………………………………………………………………………………………………

4.2 Вычесление обратной матрицы………………………………………………………………………………………….

Список литературы……………………………………………………………………………………………………………………

Что такое массив перестановок

Последние несколько строк вывода на рис. 1 указывают, что матрицы L и U можно перемножить так, чтобы получить исходную матрицу. Знание того, как это делается, не поможет вам в решении практических задач операций над матрицами, но позволит разобраться, что представляет собой часть P в разложении LUP. Восстановление исходной матрицы из ее компонентов L и U также пригодится для тестирования ваших библиотечных методов работы с матрицами на согласованность.

Один из способов восстановления исходной матрицы после разложения LUP — перемножение L и U с последующей перестановкой строк результата на основе массива P:

Метод UnPermute можно закодировать так:

Второй подход — преобразование массива perm в матрицу perm с последующим перемножением матрицы perm и комбинированной матрицы LU:

Матрица perm является квадратной с одним значением 1.0 в каждой строке и каждом столбце. Метод, который создает матрицу perm из массива perm, можно написать следующим образом:

Согласованные матрицы

Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=\left$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали

Сейчас важно другое

Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:

1. Нам важен порядок матриц. Например, матрицы $A=\left$ и $B=\left$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=\left$ и $A=\left$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
2. Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.

Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $\left$ согласованы всегда.

Ну и что с того?

Символ суммирования.

Прежде чем двигаться дальше, остановимся на обозначениях. В математике часто приходится рассматривать суммы большого числа слагаемых, имеющих сходный вид и отличающихся только индексами. Для таких сумм принято следующее обозначение. Символ \(\displaystyle\sum_{k=1}^{n}\), после которого стоит некоторое выражение, содержащее индекс \(k\), обозначает сумму таких выражений для всех значений индекса от 1 до \(n\), например,
$$
\sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+…+a_{n},\ \sum_{k=1}^{n} \alpha_{k}\beta_{k}=\alpha_{1}\beta_{1}+…+\alpha_{n}\beta_{n}.\nonumber
$$
Индекс \(k\) называется индексом суммирования. Разумеется, в качестве индекса суммирования может быть употреблена любая другая буква. На указанный символ и следующее за ним выражение можно смотреть как на скобку, содержащую \(n\) однотипных слагаемых.

Следующие формулы являются другой записью вынесения множителя за скобку и группировки слагаемых:
$$
\sum_{k=1}^{n} \alpha P_{k}=\alpha \sum_{k=1}^{n} P_{k},\label{ref1}
$$
$$
\sum_{k=1}^{n} (P_{k}+Q_{k})=\sum_{k=1}^{n} P_{k}+\sum_{k=1}^{n} Q_{k}.\label{ref2}
$$

Если имеется выражение, зависящее от двух индексов, принимающих значения \(1,…, n\) и \(1,…, m\), мы можем просуммировать сначала по одному из них, а затем полученные суммы — по-другому:
$$
\sum_{i=1}^{n} (\sum_{j=1}^{m} P_{ij}).\nonumber
$$
(Скобки обычно не пишутся.) Эта двойная сумма содержит слагаемые, соответствующие всевозможным парам значений индексов. Если мы запишем \(P_{ij}\) для всех \(i=1,…, n\) и \(j=1,…, m\) в виде матрицы, то сумма в скобках равна сумме элементов \(i\)-й строки, а во внешней сумме складываются результаты для всех строк.

То же самое число мы, конечно, получим, если сначала сложим элементы по столбцам, а затем просуммируем полученные суммы для всех столбцов. Поэтому
$$
\sum_{i=1}^{n} \sum_{j=1}^{m} P_{ij}=\sum_{j=1}^{m} \sum_{i=1}^{n} P_{ij}.\label{ref3}
$$

Классификация операций умножения матриц

Для перемножения табличных данных используют разные варианты процедур умножения:

1. Умножение на число;
2. Произведения вектора на матрицу и наоборот;
3. Взаимное умножение двух матриц.

Данные операции выполняются через удобный умножение матриц калькулятор. Каждый аспект имеет свои особенности. Например, для операций с числами есть ряд специфических закономерностей, на которые стоит опираться в момент расчетов. Это феномен идентичной матрицы, нулевой, результат перемножения суммы матриц или суммы чисел, а также закон сочетаемости разных матриц, по аналогии со свойствами умножения.

Все они являются актуальными при умножении на вектор, где тоже есть свои нюансы.

Умножение матриц

Процедура перемножения двух таблиц выполняется исключительно при одном условии – совпадении количества столбцов в структуре первого множителя и аналогичного числа строчек в составе второго множителя. В этом случае можно сказать, что две матрицы являются согласованными между собой. Также перемножение выполнимо, если сомножители являются квадратными матрицами одного типа.

Можно сделать вывод, что наличие произведения АВ не является тождественным, на первый взгляд, аналогичному произведению ВА. Первое не обуславливает существование второго.

В данном случае необходимо вспомнить также операцию с обратной матрицей. Она является «невырожденной», «неособенной», при условии, что она располагает обратной самой себе – А-1.

При этом будет соблюдаться условие:

АА-1=А-1А=Е

В противоположном случае А будет особенной, то есть «вырожденной» таблицей.

Существуют разные алгоритмы моментального перемножения матриц разного масштаба. Они применяются в сложных космических и производственных расчетах:

1) Метод Штрассена. В его основе – рекурсивное разделение таблиц на блоки со сторонами 2 х 2. Эти матрицы можно взаимно умножить некоммутативным путем через семь процедур перемножения, а не восемь. Минус этого подхода – в повышенной сложности, на фоне стандартных вычислений. Но на основе алгоритма разработан спектр других, которые формируют большую устойчивость формулы.

2) Метод Пана – его сложность составляет концентрацию n2,78041.

3) Метод Бини – алгоритм под авторством большой группы исследователей под руководством Бини, они выработали расчет умножения таблиц с применением тензоров, сложность еще выше предыдущего.

4) Метод Шенхаге – скорость расчета составляет n2,695.

5) Подход Копперсмита-Винограда наследует метод Штрассена и сегодня является самым асимптотически быстрым. Актуален на матрицах с астрономически огромными параметрами.

Выполняйте умножение матриц с помощью удобного калькулятора, не забывая о корректном вводе данных.

1.13. Ранг матрицы

Рассмотрим набор из K векторов x₁,
x₂,…,x_K размерности
N. Рангом этой системы векторов называется максимальное число
линейно-независимых векторов. Например в наборе

имеются только два линейно независимых вектора, например
x₁ и x₂, поэтому ее ранг
равен 2. 

Очевидно, что если векторов в наборе больше, чем их размерность
(K>N), то они обязательно линейно зависимы. 

Рангом
матрицы (обозначается rank(A)) называется ранг системы
векторов, из которых она состоит. Хотя любую матрицу можно представить двумя
способами (векторы столбцы или строки), это не влияет на величину ранга, т.к. 

rank(A) = rank(At).

Принцип умножения матрицы на вектор значения

Для определения значения произведения матрицы и вектора, нужно использовать правило, которое звучит как: “умножение строки на столбе”

• при умножении матрицы на векторный столбец, значение столбцов в любой матрице обязательно должно совпадать с количеством строк в вектор-столбце.
• окончательным результатом произведения векторного столбца будет являться только вектор.

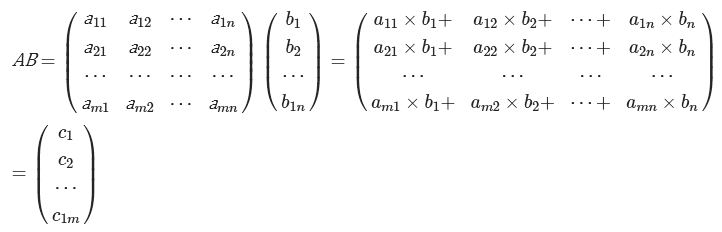
в случае, когда перемножаем векторную строку, то матрица при умножении должна быть обязательно векторным столбцом. Количество столбиков обязательно должно совпадать со значение столбцов относительно строк.

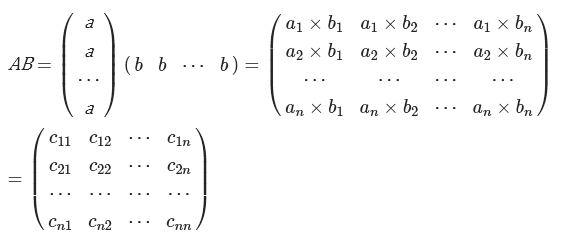
Пример решения задачи данного типа:

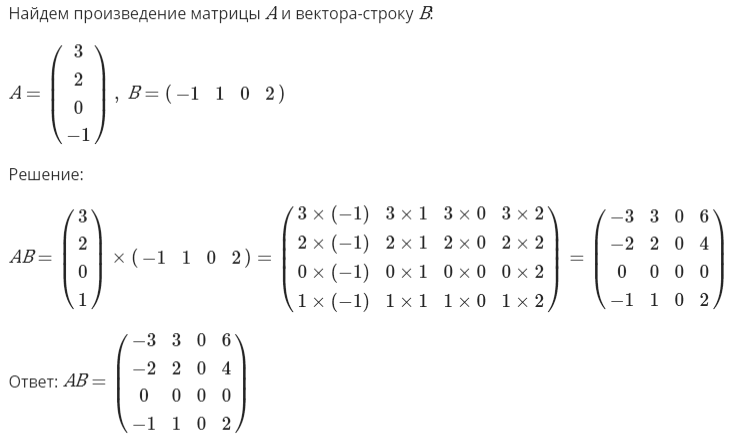
linear алгебра — Решение для X в простой системе матричных уравнений.

Задать вопрос

спросил 9 лет, 6 месяцев назад

Изменено
9 лет, 6 месяцев назад

Просмотрено
4к раз

$\begingroup$

Я пытаюсь найти X в этой простой системе матричных уравнений:

$$\begin{bmatrix}7 & 7\\2 & 4\\\end{bmatrix} — X\begin{bmatrix}5 & — 1\\6 & -4\\\end{bmatrix} = E $$, где $E$ — единичная матрица.

Если я умножу $X$ на $\begin{bmatrix}5 & -1\\6 & -4\\\end{bmatrix}$, я получу следующую систему:

$$\begin{bmatrix}5x_1 & -1x_2\\6x_3 & -4x_4\\\end{bmatrix}$$

Вычитая это из $\begin{bmatrix}7 и 7\\2 & 4\\\end{bmatrix}$ я получаю $\begin {bmatrix}7 — 5x_1 и 7 + 1x_2\\2 — 6x_3 и 4 + 4x_4\\\end{bmatrix} = \begin{bmatrix}1 & 0\\0 & 1\\\end{bmatrix}$

Что дает мне:

$7-5x_1 = 1$

$7+1x_2 = 0$

$2-6x_3 = 0$

$4+4x_4 = 1$

Это не правильные ответы, кто может помочь меня здесь?

• линейная алгебра
• матрицы

$\endgroup$

4

$\begingroup$

$$\begin{bmatrix}7 и 7\\2 & 4\\\end{bmatrix} — X\begin{bmatrix}5 & -1\\6 & -4\\\end{bmatrix} = I $$, где $I$ — единичная матрица.

Подсказка: вспомните, как будет выглядеть умножение на $X$:
$X$ будет матрицей $2\times 2$, если для этого уравнения нужно задать умножение и сложение матриц.

Итак, если $X = \begin{bmatrix} x_1 & x_2 \\ x_3 & x_4 \end{bmatrix}$, то $$X\begin{bmatrix}5 & -1\\6 & -4 \end{bmatrix } = \begin{bmatrix} x_1 & x_2 \\ x_3 & x_4 \end{bmatrix}\begin{bmatrix} 5 & -1 \\ 6 & -4\end{bmatrix} = \begin{bmatrix}5x_1+6x_2&- x_1-4x_2\\5x_3+6x_4&-x_3-4x_4\end{bmatrix}$$

$\endgroup$

7

$\begingroup$

Поскольку $\begin{pmatrix}7&7\\2&4\end{pmatrix}-X\begin{pmatrix}5&-1\\6&-4\end{pmatrix}=\begin{pmatrix}1&0\\0&1\end {pmatrix}$, получаем: $\begin{pmatrix}6&7\\2&3\end{pmatrix}=\begin{pmatrix}5x_1+6x_2&-x_1-4x_2\\5x_3+6x_4&-x_3-4x_4\end{pmatrix }$, где $X=\begin{pmatrix}x_1&x_2\\x_3&x_4\end{pmatrix}$. Теперь вы можете умножить обе части уравнения на $\frac{1}{-14}\begin{pmatrix}-4&1\\-6&5\end{pmatrix}$ =(inverse of $\begin{pmatrix}5&- 1\\6&-4\end{pmatrix}$), чтобы найти: $X=\frac{1}{-14}\begin{pmatrix}6&7\\2&3\end{pmatrix}\begin{pmatrix}- 4&1\\-6&5\end{pmatrix}=\frac{1}{-14}\begin{pmatrix}-66&41\\-26&17\end{pmatrix}$.

$\endgroup$

4

$\begingroup$

Давайте запишем ваше уравнение в виде $C-XA = E$, где $C$ — матрица констант, а $A$ — матрица коэффициентов.

Во-первых, изолируйте вашу матрицу $AX$, переместив постоянную матрицу в другую часть уравнения. манипулируйте уравнением, чтобы получить $AX$ как положительное значение. затем умножьте матрицу $A$ на обратную

Обратите внимание, что это правостороннее умножение. Теперь у вас остался вектор $X$, умноженный на тождество слева

9{-1}$ через, это не имеет значения. Просто помните, что вы выполняете умножение правой рукой, а не левой

Это важно, потому что умножение не является коммуникативным в матрицах

$\endgroup$

2

Вычисление определителя матрицы методом Гаусса.

Опишем суть этого метода. Матрица А с помощью элементарных преобразований приводится к такому виду, чтобы в первом столбце все элементы, кроме стали нулевыми (это сделать всегда возможно, если определитель матрицы А отличен от нуля). Эту процедуру опишем чуть позже, а сейчас поясним, для чего это делается. Нулевые элементы получаются для того, чтобы получить самое простое разложение определителя по элементам первого столбца. После такого преобразования матрицы А, учитывая восьмое свойство и , получим
где — минор (n-1)-ого порядка, получающийся из матрицы А вычеркиванием элементов ее первой строки и первого столбца.

С матрицей, которой соответствует минор , проделывается такая же процедура получения нулевых элементов в первом столбце. И так далее до окончательного вычисления определителя.

Теперь осталось ответить на вопрос: «Как получать нулевые элементы в первом столбце»?

Опишем алгоритм действий.

Если , то к элементам первой строки матрицы прибавляются соответствующие элементы k-ой строки, в которой . (Если все без исключения элементы первого столбца матрицы А нулевые, то ее определитель равен нулю по второму свойству и не нужен никакой метод Гаусса). После такого преобразования «новый» элемент будет отличен от нуля. Определитель «новой» матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Теперь мы имеем матрицу, у которой . При к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на . И так далее. В заключении к элементам n-ой строки прибавляем соответствующие элементы первой строки, умноженные на . Так будет получена преобразованная матрица А, все элементы первого столбца которой, кроме , будут нулевыми. Определитель полученной матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Разберем метод при решении примера, так будет понятнее.

Пример.

Вычислить определитель матрицы порядка 5 на 5 .

Решение.

Воспользуемся методом Гаусса. Преобразуем матрицу А так, чтобы все элементы ее первого столбца, кроме , стали нулевыми.

Так как изначально элемент , то прибавим к элементам первой строки матрицы соответствующие элементы, например, второй строки, так как :

Знак « ~ » означает эквивалентность.

Теперь прибавляем к элементам второй строки соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на , и аналогично действуем вплоть до шестой строки:

Получаем

С матрицей проводим ту же процедуру получения нулевых элементов в первом столбце:

Следовательно,

Сейчас выполняем преобразования с матрицей :

Получаем

Матрица уже имеет необходимый вид, поэтому

Ответ:

.

Рассмотрим решение еще одного примера, но подробно описывать действия не будем. Это некоторый образец краткой записи вычисления определителя матрицы методом Гаусса.

Пример.

Вычислите определитель матрицы порядка 7 на 7.

Решение.

Следовательно,

Замечание.

На некотором этапе преобразования матрицы по методу Гаусса может возникнуть ситуация, когда все элементы нескольких последних строк матрицы станут нулевыми. Это будет говорить о равенстве определителя нулю.

Подведем итог.

Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:

1. через сумму произведений сочетаний элементов матрицы;
2. через разложение определителя по элементам строки или столбца матрицы;
3. методом приведения матрицы к верхней треугольной (методом Гаусса).

Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.

Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.

При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.

Некогда разбираться?

1.4. Квадратные матрицы

Если число столбцов матрицы равно числу ее строк (I = J =
N), то такая матрица называется квадратной. В этом разделе мы будем
рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы,
обладающие особыми свойствами.

Единичной матрицей (обозначается I, а иногда
E) называется матрица, у которой все элементы равны нулю, за
исключением диагональных, которые равны 1, т.е.

Очевидно AI = IA = A.

Матрица называется диагональной, если все ее элементы, кроме
диагональных (a_ii) равны нулю. Например

Рис.
8 Диагональная матрица

Матрица A называется верхней треугольной, если все
ее элементы, лежащие ниже диагонали, равны нулю, т.е. a_ij =
0, при i>j. Например

Рис.
9 Верхняя треугольная матрица

Аналогично определяется и нижняя треугольная матрица.

Матрица A называется симметричной, если
At = A. Иными словами
a_ij = a_ji. Например

Рис. 10
Симметричная матрица

Матрица A называется ортогональной, если 

AtA =
AAt = I.

Матрица называется нормальной если

 
AtA =
AAt.