Метод элементарных преобразований (методы гаусса и гаусса-жордана для нахождения обратных матриц)

Влияние элементарных матриц на другие матрицы

Пусть A — матрица , и матрицы типа 1, типа 2 и типа 3 соответственно.
п×м{\ Displaystyle п \ раз м}Р.я,j(α){\ Displaystyle R_ {я, j} (\ альфа)}Тя,j{\ displaystyle T_ {i, j}}С.я(γ){\ Displaystyle S_ {я} (\ гамма)}

Умножение слева дает линейные преобразования:

• С.я(γ)⋅А.{\ Displaystyle S_ {я} (\ гамма) \ cdot A}умножает i-ю строку A на значение , при этом остальные строки остаются неизменными (EZU I)γ{\ displaystyle \ gamma}
• Р.я,j(α)⋅А.{\ Displaystyle R_ {я, j} (\ альфа) \ cdot A}добавляет -кратность j-й строки A к i-й строке A. (EZU II)α{\ displaystyle \ alpha}
• Тя,j⋅А.{\ Displaystyle T_ {я, j} \ cdot A} меняет местами i-ю строку A с j-й строкой A. (EZU III)

Умножение справа приводит к преобразованию столбцов:

А.⋅С.я(γ){\ Displaystyle А \ cdot S_ {я} (\ гамма)}умножает i-й столбец A на значение , оставляя остальные столбцы без изменений. (ESU I)γ{\ displaystyle \ gamma}

А.⋅Р.я,j(α){\ Displaystyle А \ cdot R_ {я, j} (\ альфа)}добавляет сгиб i-го столбца A к j-му столбцу A

(ESU II) Обратите внимание на то, что значения i и j меняются местами в отличие от преобразования строк.α{\ displaystyle \ alpha}

А.⋅Тя,j{\ Displaystyle A \ cdot T_ {я, j}} меняет местами i-й столбец A с j-м столбцом A. (ESU III)

См. Также матричное умножение . Эти свойства важны для методов решения матричных вычислений, таких как алгоритм Гаусса-Жордана .

Напоминание: чтобы построить соответствующую элементарную матрицу для одного из вышеупомянутых преобразований, соответствующее преобразование должно быть применено к единичной матрице . Например, чтобы получить элементарную матрицу, которая меняет местами первую и вторую строки матрицы, первая и вторая строки единичной матрицы меняются местами, что приводит к.
Я.п{\ displaystyle I_ {n}}Т1,2{\ displaystyle T_ {1,2}}

Метод Гаусса

Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:

• действия, когда в системе переставляются местами два уравнения;
• произведение одного из уравнений в системе на действительное ненулевое число;
• сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.

Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.

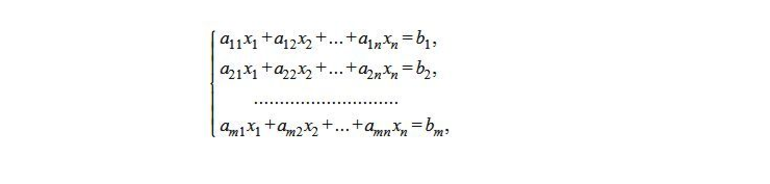
Следует переписать эту систему в матричный вид:

В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.

Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:

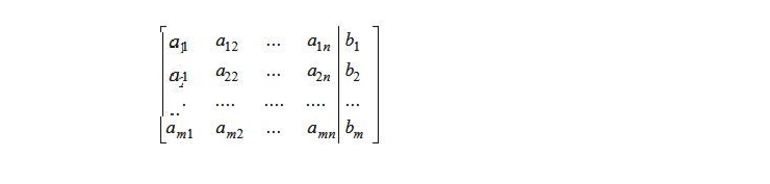
Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:

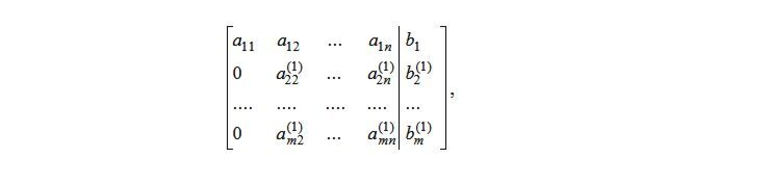
На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 ..m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:

Обращают внимание на последние строки

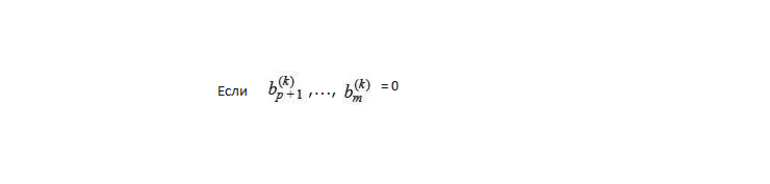
В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).

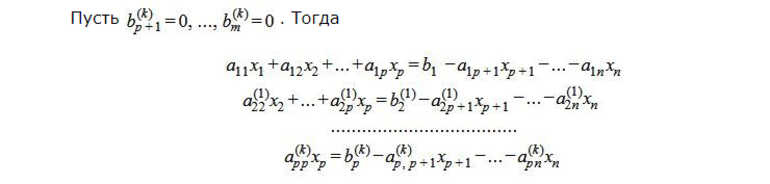
Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.

Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».

Решение матричных уравнений

Финальная глава саги.

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.

Краткое содержание прошлых частей:

• Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
• Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
• Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
• Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
• Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
• Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Ранг матрицы — определение и вычисление с примерами решения

Элементарные преобразования матриц:

Рассмотрим прямоугольную матрицу:

состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:

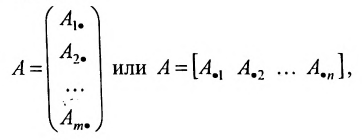
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).

Третий шаг

На третьем шаге мы работаем с третьей строкой. В третьей строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента третьей строки $k=4$. Посмотрим на строки, расположенные под третьей строкой. Ведущие элементы в этих строках имеют номера 4 и 4, наименьший из которых $k_{\min}=4$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы четвёртой и пятой строк. Преобразования, которые выполняются с этой целью, полностью аналогичны тем, что осуществлялись ранее:

Под третьей строкой остались лишь нулевые строки. Это значит, что преобразования закончены. Мы привели матрицу к ступенчатому виду. Так как приведённая матрица содержит три ненулевых строки, то её ранг равен 3. Следовательно, и ранг исходной матрицы равен трём, т.е. $\rang A=3$. Полное решение без пояснений таково:

Ответ: $\rang A=3$.

Пример №2

Найти ранг матрицы $A=\left(\begin{array}{ccccc}
11 & -13 & 61 & 10 & -11\\
2 & -2 & 11 & 2 & -2\\
-3 & 5 & -17 & -2 & 3\\
4 & 0 & 24 & 7 & -8
\end{array} \right)$.

Решение

Данная матрица не является нулевой, а значит её ранг больше нуля. Перейдём к первому шагу алгоритма.

Матрицы

Термин «матрица» был введен Дж. Сильвестром в 1850 году, в математику — А. Кэли в 1857 году. Матрицей называется математический объект, состоящий из элементов, взятых в определенном порядке.

Для указания на порядок элементов матрицы их выписывают в виде таблицы из строк и столбцов. Элемент матрицы, стоящий на пересечении строки с номером и столбца с номером обозначают Если — числа, матрица называется числовой. Обозначают матрицы большими латинскими буквами. Обозначение матриц

где

Иногда матрицу обозначают одной буквой, например,

Основные виды матриц

Если число строк матрицы равно числу ее столбцов, т. е. то матрица называется квадратной. Порядком квадратной матрицы называется число ее строк (или столбцов). Строки и столбцы матрицы называют ее рядами.

Обозначение квадратной матрицы порядка

— квадратная матрица 3-го порядка.

Две матрицы называются равными, если они имеют одинаковые размеры и элементы одной матрицы равны соответствующим элементам другой матрицы:

В квадратной матрице элементы образуют главную диагональ, а элементы — побочную. Диагональной матрицей называется квадратная матрица, у которой отличны от нуля только элементы, стоящие по главной диагонали.

Диагональной матрицей называется квадратная матрица, у которой отличны от нуля только элементы, стоящие по главной диагонали.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной Например,

Нулевой матрицей называется матрица, все элементы которой равны нулю:

Симметрическая матрица — квадратная матрица, для которой Например, матрица симметрическая.

Трапециевидная матрица — матрица произвольных размеров, если она имеет вид

где отличны от нуля.

Треугольная матрица (частный случай трапециевидной) -квадратная матрица, все элементы которой по одну или другую сторону от главной диагонали равны нулю. Различают верхнюю и нижнюю треугольные матрицы. Например, матрица вида

называется верхней треугольной матрицей.

Матрица полученная из данной матрицы заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной.

Если

то

Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы. Матрица, состоящая из одной строки, называется матрицей-строкой. Она имеет вид Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Имеет вид

Действия над матрицами

К линейным операциям над матрицами относятся умножение матрицы на число, сложение матриц.

1. Умножение, матрицы на число. Произведением матрицы на действительное число называется новая матрица где Обозначение: Например,

Матрица вида называется матрицей, противоположной матрице

Сложение, матриц

Складывать можно только матрицы одинаковых размеров, т. е. имеющие одинаковое число строк и столбцов.

Суммой двух матриц и называется матрица где и обозначается

Пример №1.1.

Разность матриц определяется так:

Умножение, матриц

Матрицу будем называть согласованной с матрицей если число столбцов матрицы равно числу строк матрицы

Пример №1.2.

Пусть

Матрица согласована с матрицей но матрица не согласована с матрицей

Если матрица согласована с матрицей то произведением матрицы на матрицу называется новая матрица такая, что

Формула (1.1) называется правилом произведения матриц. Из определения произведения матриц следует, что для того, чтобы получить элемент произведения матриц стоящий в строке и столбце, нужно умножить элементы строки матрицы на соответствующие элементы столбца матрицы и эти произведения сложить.

Пример №1.3.

Вычислить если

Решение:

Матрица (три столбца) согласована с матрицей (три строки).

Замечание. Умножить матрицу на в данном случае нельзя — число столбцов матрицы (три) не равно числу строк матрицы (двум).

Замечание. Так как в общем случае то произведение матриц не коммутативно.

Матричные операции

В этом разделе описываются основные операции, определенные в массивах.

Добавление. Сумма A + B двух матриц получается путем сложения соответствующих элементов A и B:

A + B = a*ij* + b*ij* = a*ij* + b*ij*

Скалярное умножение. Эта операция умножает матрицу на действительное число. Для действительного числа k скалярное произведение получается путем умножения каждого элемента A на k.

kA = ka*ij* = k × a*ij*

Умножение матриц. Для двух матриц A и B порядка (m × n) и (n × p) произведение C = A × B представляет собой матрицу порядка (m × p), определяемую следующим образом:

или эквивалент:

c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* +… + a*in* + b*nj*

То есть, чтобы вычислить каждый элемент cij, сделайте следующее.

1. Возьмите i-ю строку A и J-й столбец B.
2. Умножьте каждую пару элементов в строке и столбце: запись в первой строке на запись в первом столбце, запись во второй строке на запись во втором столбце и т д
3. Резюме результата.

Ниже приведен пример умножения матрицы (2×2) на матрицу (2×3).

Умножение матриц не является коммутативным. То есть A × B ≠ B × A. Кроме того, из определения следует, что не всякую пару матриц можно перемножать. Количество столбцов в левой матрице должно быть равно количеству строк в правой матрице. В противном случае оператор × не определен.

Определение матрицы. Единичная матрица, обозначенная I, представляет собой квадратную матрицу, определяемую следующим образом:

I*ij* = 1, если *i* = *j*, или 0 в противном случае.

Другими словами, единичная матрица содержит 1 для каждого элемента, где номер строки равен номеру столбца, и ноль для всех остальных элементов. Например, вот массив идентификаторов 3×3.

Для любой матрицы M хранятся следующие равные значения.

МхИ=МИхМ=М

Определение

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;
• умножение любой строки матрицы на константу , ;
• прибавление к любой строке матрицы другой строки, умноженной на константу , .

В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу , и прибавление к любой строке матрицы другой строки, умноженной на константу , .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение указывает на то, что матрица может быть получена из путём элементарных преобразований (или наоборот).

Элементарные преобразования системы линейных уравнений

Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:

1) перестановка любых двух уравнений местами;

2) умножение обеих частей одного уравнения на любое число

3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;

(при этом все остальные уравнения остаются неизменными).

Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.

Доказательство. В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.

1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной.

2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число

Пусть решение системы (1) . Тогда числа

Умножая его на число K, получим верное числовое равенство:

Т. о. устанавливаем, что  решение системы (2).

Обратно, если решение системы (2), то числа



Отсюда по определению 4 система (1) равносильна системе (2).

3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы. Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число K , получим систему

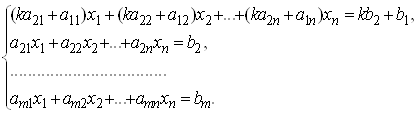
Пусть решение системы (1) . Тогда числа

Прибавляя почленно к первому равенству второе, умноженное на число K получим верное числовое равенство:

Обратно, если решение системы (5), то числа

K

Отсюда по определению 4 система (1) равносильна системе (5).

4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.

Презентация на тему: » 1.2. Элементарные преобразования матриц Определение 1.7. Элементарными преобразованиями матрицы А называются следующие преобразования: 1) перестановка.» — Транскрипт:

1

1.2. Элементарные преобразования матриц Определение 1.7. Элементарными преобразованиями матрицы А называются следующие преобразования: 1) перестановка любых двух строк (столбцов) в матрице; 2) умножение любой строки (столбца) на любое ненулевое число; 3) прибавление к любой строке (столбцу) другой строки (столбца), умноженной на любое число. Матрицы А и В называются эквивалентными (А В), если они получаются одна из другой с помощью цепочки элементарных преобразований.

2

Пример 1.1. ~ ~ Теорема 1.2. Любую квадратную матрицу можно с помощью цепочки элементарных преобразований привести к «треугольному» виду. Пример 1.2. ~ ~ ~ ~ Все элементы 1-ой строки умножаем на число (-4), затем результат прибавляем к 3-ей строке (на неё указывает стрелка) Переставляем первую и вторую строки с целью: в «левом верхнем углу» получить 1

3

Теорема 1.3. Любую прямоугольную (неквадратную) матрицу А можно с помощью цепочки элементарных преобразований привести к, так называемому, «почти треугольному» виду или к «ступенчато– треугольному» виду. Замечание. «Ступенчато–треугольной» матрицей назовем матрицу «почти треугольного» вида, у которой в каждой следующей строке (начиная со второй строки) количество нулевых элементов подряд (начиная с левого конца этой строки) больше, чем в предыдущей строке. Примеры 1.3. ~ ~ ~ ~ ~ ~

4

1.4. ~ ~ ~ 1.5. ~ 1.6. ~ ~ 1.3. Ранг матрицы Определение 1.8. Пусть дана матрица А, которая (согласно теоремам 1.2 и 1.3) может быть приведена к треугольному или «почти треугольному» виду (или «ступенчато–треугольному» виду). Количество базисных элементов в преобразованной матрице называется рангом матрицы (и одновременно рангом преобразованной матрицы). Ранг матрицы обозначается через.

5

Замечание. Ранг можно определить и как количество ненулевых строк в матрице «ступенчато треугольного» вида. Например. В примере 1.4 базисных элементов в преобразованной матрице – два, ненулевых строк в преобразованной матрице «ступенчато треугольного» вида – тоже два: В примере 1.6: 1.4. Определитель матрицы. Свойства определителей Определение 1.9. Пусть дана квадратная матрица А. Согласно теореме 1.2 её можно с помощью цепочки элементарных преобразований (алгоритм Гаусса) привести к треугольному виду:

6

Тогда число, (1.11) где р – число перестановок строк в алгоритме Гаусса, с помощью которого из А получена, называется определителем матрицы А. Пример 1.7. Найти определитель матрицы А: ~ ~ ~ ~ ~ Свойства определителей 1. Пусть Е – единичная матрица, тогда (1.12)

7

2. Пусть – диагональная матрица, тогда.(1.13) 3. Пусть – матрица «треугольного» вида, тогда.(1.14) 4. Если – матрица размера 1 1, то. (1.14.1) 5. Если – матрица размера, тогда. (1.15)

8

Определение Пусть – квадратная матрица, – её элемент, тог- да минором этого элемента называется число, равное определителю матрицы, которая получается из матрицы А «вычеркиванием» её i–ой строки и j–го столбца. Алгебраическим дополнением элемента назы- вается число. 6. Пусть А – квадратная матрица, тогда её определитель может быть вычислен «разложением по любой строке (или любому столбцу)». Например, «разлагая по первой строке», получим:.(1.16)

9

Пример 1.8. Замечание.

10

7. Если в квадратной матрице А имеется чисто нулевая строка (столбец), то определитель такой матрицы равен нулю. Свойство 8 следует из свойства Пусть А и В – квадратные матрицы одинакового размера, которые полу- чаются друг из друга с помощью цепочки элементарных преобразований типа 1) и 3) (см. определение 1.7), тогда, (1.17) где р – число перестановок строк в цепочке элементарных преобразований при переходе от А к В (или от В к А ). 9. Если в матрице А имеются две пропорциональные строки (столбца), то её определитель равен нулю. Пример 1.9. В матрице: – первая и вторая строки пропорци- ональны:. Далее: ~, поэтому по свойству 9, но по свойству 8, то есть. 10. Если А и В – две квадратные матрицы одинакового размера, то

11

11. Если матрица А имеет к себе обратную, то Метод нахождения обратной матрицы Теорема 1.4. Пусть А – матрица размера. Если, то такая матрица имеет к себе обратную. При этом обратную матрицу можно найти так: » (1.18) Замечание. Если же, то обратная матрица не существует (см. замечание к определению 1.6). Пример Найти обратную матрицу к матрице. Решение Имеем:, поэтому по теореме 1.4 матрица А имеет обратную:. (1.19)

12

Далее: Из (1.19) получаем:. Проверка: Ответ:.

Обратный ход метода Гаусса

Первый шаг

На первом шаге обратного хода мы работаем с последней, т.е. третьей строкой матрицы. Посмотрим на диагональный элемент в третьей строке: он равен $-\frac{2}{3}$. Сделаем этот элемент единицей, домножив третью строку на $-\frac{3}{2}$, а затем с помощью третьей строки обнулим ненулевые элементы третьего столбца, расположенные над третьей строкой:

Второй шаг

На втором шаге обратного хода мы работаем с предпоследней, т.е. второй строкой матрицы. Посмотрим на диагональный элемент во второй строке: он равен 3. Сделаем этот элемент единицей, домножив вторую строку на $\frac{1}{3}$, а затем с помощью второй строки обнулим ненулевой элемент второго столбца, расположенный над второй строкой:

Третий шаг

Работаем с первой строкой. Сделаем диагональный элемент в первой строке (число -1) равным единице, домножив первую строку на -1:

Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:

Если пропустить все пояснения, то решение будет таким:

Теперь решим этот же пример методом Гаусса-Жордана.

Композиция преобразований

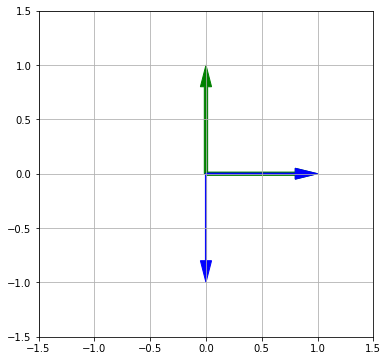
Посмотрим, что произойдет, если применить сначала поворот на 90 градусов по часовой стрелке, затем отражение относительно оси y.

Так как матрица преобразования стоит слева от преобразуемого вектора, то для применения двух преобразований, матрица второго преобразования будет стоять слева от матрицы первого.

$$ Reflect_y \cdot (Rotate \cdot \mathbf x ) $$

Подготовим матрицы.

1 2 3 4 5 6 7

# поворот по часовой стрелки theta=np.radians(90) Rotate=np.array(np.cos(theta),np.sin(theta), -np.sin(theta),np.cos(theta)).round()   Rotate

1 2	array(,        ])

1 2 3 4 5

# отражение относительно оси y Reflect_y=np.array(-1,, ,1)   Reflect_y

1 2	array(,        ])

Выполним преобразование.

1	np.dot(Reflect_y,np.dot(Rotate,i)),np.dot(Reflect_y,np.dot(Rotate,j))

1	(array(), array())

Посмотрим на этот процесс графически. Вначале первое преобразование (вращение).

1 2 3 4 5 6 7 8 9 10 11 12 13 14

ax=plt.axes() plt.xlim(-1.5,1.5) plt.ylim(-1.5,1.5) plt.grid() ax.arrow(,,i,i1,width=0.03,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’) ax.arrow(,,j,j1,width=0.03,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’)   # поворот по часовой стрелке ax.arrow(,,np.dot(Rotate,i),np.dot(Rotate,i)1,width=0.01,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) ax.arrow(,,np.dot(Rotate,j),np.dot(Rotate,j)1,width=0.01,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) plt.show()

Теперь применим второе преобразование (отражение) к результату первого.

1 2 3 4 5 6 7 8 9 10 11 12 13 14

ax=plt.axes() plt.xlim(-1.5,1.5) plt.ylim(-1.5,1.5) plt.grid() ax.arrow(,,i,i1,width=0.03,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’) ax.arrow(,,j,j1,width=0.03,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’)   # отображение относительно оси y ax.arrow(,,np.dot(Reflect_y,np.dot(Rotate,i)),np.dot(Reflect_y,np.dot(Rotate,i))1,width=0.01,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) ax.arrow(,,np.dot(Reflect_y,np.dot(Rotate,j)),np.dot(Reflect_y,np.dot(Rotate,j))1,width=0.01,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) plt.show()

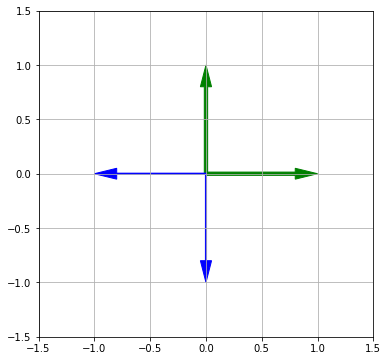
Запишем, где оказались векторы $\mathbf i$ и $\mathbf j$ после второго преобразования и соединим эти координаты в матрицу. Затем умножим на исходные векторы $\mathbf i$ и $\mathbf j$.

1 2 3 4

Composition=np.array(,-1, -1,) np.dot(Composition,i),np.dot(Composition,j)

1	(array(), array())

Результат аналогичен последовательному применению предыдущих преобразований.

1 2	# то же самое мы получим, перемножив матрицы преобразований np.dot(Reflect_y,Rotate)

1 2	array(,        ])

Обратите внимание, что порядок операций важен. Поменяв матрицы преобразований местами, мы получим другой результат

1 2 3

# выполнив отражение, а затем поворот, # мы вернем векторы в исходное положение np.dot(Rotate,np.dot(Reflect_y,i)),np.dot(Rotate,np.dot(Reflect_y,j))

1	(array(), array())

Это еще раз демонстрирует некоммутативность, но ассоциативность умножения матриц.

Приведем ссылки на видео:

• Умножение матриц как последовательность преобразований⧉
• Линейные преобразования в трехмерном пространстве⧉

Определение и виды элементарных преобразований

Элементарными называются такие преобразования матрицы, при которых сохраняется эквивалентность матриц (из-за этого их часто называют эквивалентными). Другими словами такие преобразования не меняют множество решений СЛАУ, которая представлена данной матрицей.

Элементарные преобразования применяются в метода Гаусса, чтобы привести матрицу к треугольному или ступенчатому виду.

К элементарным преобразованиям относятся:

• перестановка двух любых строк местами;
• умножение любой строки на ненулевую константу;
• сумма двух любых строк, одна из которых умножена на определенное ненулевое число.

Примечание: аналогичные действия применимы и к столбцам матрицы.

Матрицы A и B являются эквивалентными, если B получена путем элементарных преобразований A (или наоборот). Для обозначения эквивалентности используется специальный символ – “

Вычисление определителя матрицы методом Гаусса.

Опишем суть этого метода. Матрица А с помощью элементарных преобразований приводится к такому виду, чтобы в первом столбце все элементы, кроме стали нулевыми (это сделать всегда возможно, если определитель матрицы А отличен от нуля). Эту процедуру опишем чуть позже, а сейчас поясним, для чего это делается. Нулевые элементы получаются для того, чтобы получить самое простое разложение определителя по элементам первого столбца. После такого преобразования матрицы А, учитывая восьмое свойство и , получим
где — минор (n-1)-ого порядка, получающийся из матрицы А вычеркиванием элементов ее первой строки и первого столбца.

С матрицей, которой соответствует минор , проделывается такая же процедура получения нулевых элементов в первом столбце. И так далее до окончательного вычисления определителя.

Теперь осталось ответить на вопрос: «Как получать нулевые элементы в первом столбце»?

Опишем алгоритм действий.

Если , то к элементам первой строки матрицы прибавляются соответствующие элементы k-ой строки, в которой . (Если все без исключения элементы первого столбца матрицы А нулевые, то ее определитель равен нулю по второму свойству и не нужен никакой метод Гаусса). После такого преобразования «новый» элемент будет отличен от нуля. Определитель «новой» матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Теперь мы имеем матрицу, у которой . При к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на . И так далее. В заключении к элементам n-ой строки прибавляем соответствующие элементы первой строки, умноженные на . Так будет получена преобразованная матрица А, все элементы первого столбца которой, кроме , будут нулевыми. Определитель полученной матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Разберем метод при решении примера, так будет понятнее.

Пример.

Вычислить определитель матрицы порядка 5 на 5 .

Решение.

Воспользуемся методом Гаусса. Преобразуем матрицу А так, чтобы все элементы ее первого столбца, кроме , стали нулевыми.

Так как изначально элемент , то прибавим к элементам первой строки матрицы соответствующие элементы, например, второй строки, так как :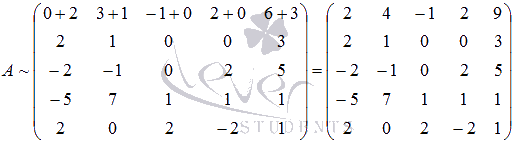

Знак « ~ » означает эквивалентность.

Теперь прибавляем к элементам второй строки соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на , и аналогично действуем вплоть до шестой строки: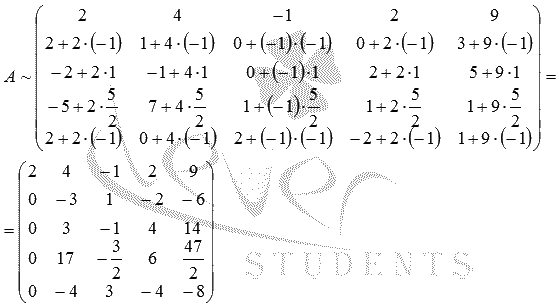

Получаем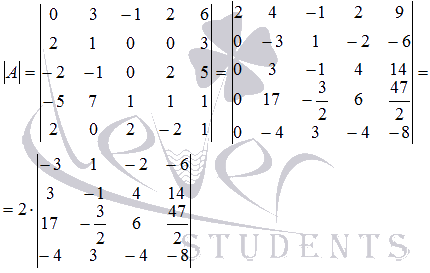

С матрицей проводим ту же процедуру получения нулевых элементов в первом столбце: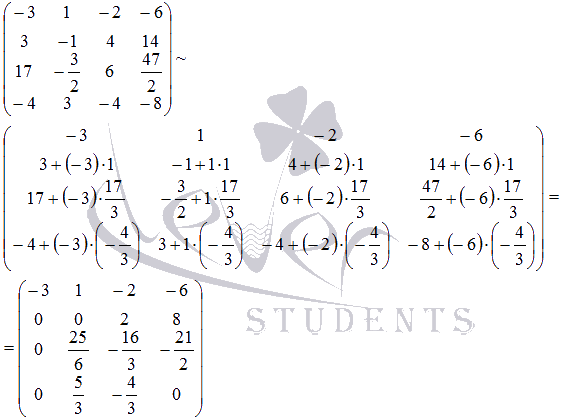

Следовательно,

Сейчас выполняем преобразования с матрицей :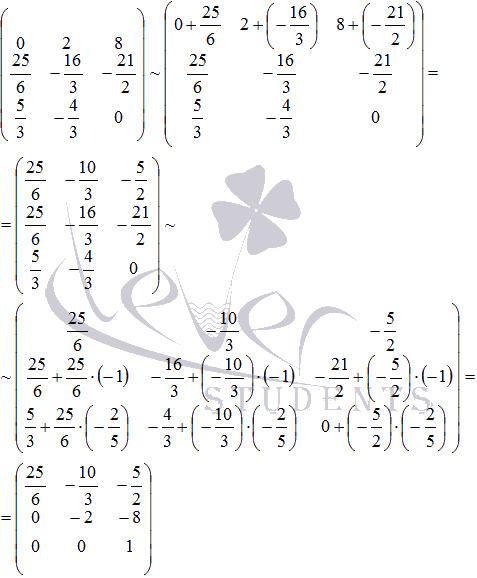

Получаем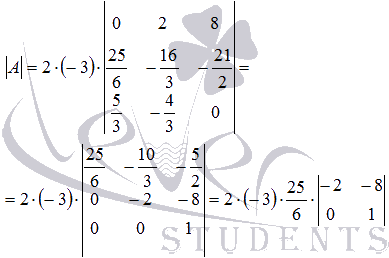

Матрица уже имеет необходимый вид, поэтому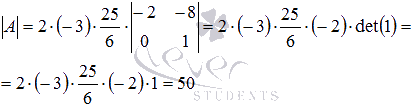

Ответ:

.

Рассмотрим решение еще одного примера, но подробно описывать действия не будем. Это некоторый образец краткой записи вычисления определителя матрицы методом Гаусса.

Пример.

Вычислите определитель матрицы порядка 7 на 7.

Решение.

Следовательно,

Замечание.

На некотором этапе преобразования матрицы по методу Гаусса может возникнуть ситуация, когда все элементы нескольких последних строк матрицы станут нулевыми. Это будет говорить о равенстве определителя нулю.

Подведем итог.

Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:

1. через сумму произведений сочетаний элементов матрицы;
2. через разложение определителя по элементам строки или столбца матрицы;
3. методом приведения матрицы к верхней треугольной (методом Гаусса).

Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.

Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.

При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.

Некогда разбираться?