Метод гаусса это треугольник

Асимптотика

Оценим асимптотику полученного алгоритма. Алгоритм состоит из фаз, на каждой из которых происходит:

• поиск и перестановка опорного элемента — за время при использовании эвристики «partial pivoting» (поиск максимума в столбце)
• если опорный элемент в текущем столбце был найден — то прибавление текущего уравнения ко всем остальным уравнениям — за время

Очевидно, первый пункт имеет меньшую асимптотику, чем второй. Заметим также, что второй пункт выполняется не более раз — столько, сколько может быть зависимых переменных в СЛАУ.

Таким образом, итоговая асимптотика алгоритма принимает вид .

При эта оценка превращается в .

Заметим, что когда СЛАУ рассматривается не в поле действительных чисел, а в поле по модулю два, то систему можно решать гораздо быстрее — об этом см. ниже в разделе «Решение СЛАУ по модулю».

Более точная оценка числа действий

Для простоты выкладок будем считать, что .

Как мы уже знаем, время работы всего алгоритма фактически определяется временем, затрачиваемым на исключение текущего уравнения из остальных.

Это может происходить на каждом из шагов, при этом текущее уравнение прибавляется ко всем остальным. При прибавлении работа идёт только со столбцами, начиная с текущего. Таким образом, в сумме получается операций.

Главное преступление учителя математики

Вряд ли после того случая
Карл Гаусс испытал высокое чувство уважения по отношению к школьному учителю математики. Но если бы он знал, как последователи того учителя
извратят самую суть метода
… он взревел бы от негодования и через Всемирную организацию интеллектуальной собственности ВОИС добился запрета на использование своего честного имени в школьных учебниках!..

В чем главная ошибка школьного подхода
? Или, как я выразился — преступление школьных учителей математики против детей?

Алгоритм непонимания

Что делают школьные методисты, абсолютное большинство которых думать не умеет ни фига?

Создают методики и алгоритмы (см. ). Это защитная реакция, предохраняющая учителей от критики («Все делается согласно…»), а детей — от понимания. И таким образом — от желания критиковать учителей!
(Вторая производная чиновничьей «мудрости», научный подход к проблеме ). Человек не улавливая смысл скорее будет пенять на собственное непонимание, а не на тупость школьной системы.

Что и происходит: родители пеняют на детей, а учителя… то же на детей, «не понимающих математику!..

Смекаете?

Что сделал маленький Карл?

Абсолютно нешаблонно подошел к шаблонной задаче
. Это квинтэссенция Его подхода. Это главное, чему следует учить в школе: думать не учебниками, а головой
. Конечно, есть и инструментальная составляющая, которую вполне можно использовать… в поисках более простых и эффективных методов счета
.

Метод Гаусса по-Виленкину

В школе учат, что метод Гаусса состоит в том, чтобы

попарно
находить суммы чисел, равноотстоящих от краев числового ряда, непременно начиная с краев
!
находить число таких пар и т.д.

что, если число элементов ряда окажется нечетным
, как в задаче, которую задали сыну?..

«Подвох» состоит в том, что в этом случае следует обнаружить «лишнее» число ряда
и прибавить его к сумме пар. В нашем примере это число 260
.

Как обнаружить? Переписывая все пары чисел в тетрадь!
(Именно почему учительница заставила детей делать эту тупую работу, пытаясь научить «творчеству» методом Гаусса… И именно поэтому такой «метод» практически неприменим к большим рядам данных, И именно поэтому он не является методом Гаусса).

Немного творчества в школьной рутине…

Сын же поступил иначе.

Сначала он отметил, что умножать легче число 500, а не 520

(20 + 500, 40 + 480 …).

Потом он прикинул: количество шагов оказалось нечетным: 500 / 20 = 25.

Тогда он в начало ряда добавил НОЛЬ (хотя можно было и отбросить последний член ряда, что также обеспечило бы четность) и сложил числа, дающие в сумме 500

0+500, 20+480, 40+460 …

26 шагов это 13 пар «пятисоток»: 13 х 500 = 6500..

Если мы отбросили последний член ряда, то пар будет 12, но к результату вычислений следует не забыть прибавить «отброшенную» пятисотку. Тогда: (12 х 500) + 500 = 6500 !

Несложно, правда?

А практически делается еще легче, что и позволяет выкроить 2-3 минуты на ДЗ по русскому, пока остальные «считают». К тому же сохраняет количество шагов методики: 5, что не позволяет критиковать подход за антинаучность.

Явно этот подход проще, быстрее и универсальнее, в стиле Метода. Но… учительница не то, что не похвалила, но и заставила переписать «правильным образом» (см. скриншот). То есть предприняла отчаянную попытку задушить творческий импульс и способность понимать математику на корню! Видимо, чтобы потом наняться репетитором… Не на того напала…

Все, что я так долго и нудно описал можно объяснить нормальному ребенку максимум за полчаса. Вместе с примерами.

Причем так, что он это никогда не забудет.

И это будет шаг к пониманию
… не только математики.

Признайтесь: сколько раз в жизни вы складывали методом Гаусса? И я ни разу!

Но инстинкт понимания
, который развивается (или гасится) в процессе изучения математических методов в школе… О!.. Это поистине незаменимая вещь!

Особенно в век всеобщей цифровизации, в который мы незаметно вошли под чутким руководством Партии и Правительства.

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

СЛАУ в зависимости от её элементов может иметь:

1. Одно решение;
2. много решений;
3. совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

• перемена мест уравнений системы;
• почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
• сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если

Множественные числа

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице

Если квадратная матрица равна нулю, она называется вырожденная, а если

невырожденная

Если с системой уравнений:

Произвести такие действия:

• умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
• менять местами уравнения;
• к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Метод Гаусса – теорема, примеры решений

Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Система, обладающая множеством возможных вариантов решений

Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).

Переменные в такой системе делятся на два вида: базисные и свободные.
При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.

У такой системы есть только некое общее решение.

Разберём следующую систему уравнений:

$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 — 4y_4 = 1 \end{cases}$

Запишем её в виде матрицы:

$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$

Наша задача найти общее решение системы.
Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ — так как он стоит на первом месте, а в случае $y_3$ — располагается после нулей).

В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.

Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.

$5y_3 – 4y_4 = 1$

$5y_3 = 4y_4 + 1$

$y_3 = \frac{4/5}y_4 + \frac{1}{5}$.

Теперь в верхнее уравнение системы $2y_1 + 3y_2 + y_4 = 1$ подставляем выраженное $y_3$:
$2y_1 + 3y_2 — (\frac{4}{5}y_4 + \frac{1}{5}) + y_4 = 1$

Выражаем $y_1$ через свободные переменные $y_2$ и $y_4$:

$2y_1 + 3y_2 — \frac{4}{5}y_4 — \frac{1}{5} + y_4 = 1$

$2y_1 = 1 – 3y_2 + \frac{4}{5}y_4 + \frac{1}{5} – y_4$

$2y_1 = -3y_2 — \frac{1}{5}y_4 + \frac{6}{5}$

$y_1 = -1.5x_2 – 0.1y_4 + 0.6$

Решение готово.

Пример 1

Решить слау методом Гаусса. Примеры.
Пример решения системы линейных уравнений заданных матрицей 3 на 3 используя метод Гаусса

$\begin{cases} 4x_1 + 2x_2 – x_3 = 1 \\ 5x_1 + 3x_2 — 2x^3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$

Запишем нашу систему в виде расширенной матрицы:

$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$

Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.

Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:

$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$

Далее к средней строчке прибавим верхнюю, умноженную на $5$, а последнюю строчку преобразуем, умножив первую строчку на 3 и сложив с последней, получаем:

$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$

Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$

Далее сложим последнюю строчку с удвоенной средней:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$

И разделим последнюю строчку на $3$:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$

Получаем следующую систему уравнений, равносильную исходной:

$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$

Из верхнего уравнения выражаем $x_1$:

$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.

Пример 2

Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса

$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.

В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.

Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$

Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$

Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$

Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$

Решаем полученную систему уравнений:

$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$

$y=2$, $x = 0$.

Как решить систему линейных уравнений методом Гаусса: принцип, пример

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Метод Гаусса для решения СЛАУ

В данной публикации мы рассмотрим, что такое метод Гаусса, зачем он нужен, и в чем заключается его принцип. Также мы на практическом примере продемонстрируем, как метод можно применить для решения системы линейных уравнений.

• Описание метода Гаусса
• Принцип метода Гаусса
• Пример решения СЛАУ

Описание метода Гаусса

Метод Гаусса – классический способ последовательного исключения переменных, применяемый для решения системы линейных уравнений. Назван так в честь немецкого математика Карла Фридриха Гаусса (1777 – 1885).

Но для начала напомним, что СЛАУ может:

• иметь одно единственное решение;
• иметь бесконечное множество решений;
• быть несовместной, т. е. не иметь решений.

Практическая польза

Метод Гаусса – отличный способ решить СЛАУ, которая включает более трех линейных уравнений, а также систем, не являющихся квадратными.

Принцип метода Гаусса

Метод включает следующие этапы:

1. прямой – расширенная матрица, соответствующая системе уравнений, путем элементарных преобразований над строками приводится к верхнему треугольному (ступенчатому) виду, т.е. под главной диагональю должны находиться только элементы, равные нулю.
2. обратный – в полученной матрице элементы над главной диагональю также обнуляются (нижний треугольный вид).

Пример решения СЛАУ

Давайте решим систему линейных уравнение ниже, воспользовавшись методом Гаусса.

Решение

1. Для начала представим СЛАУ в виде расширенной матрицы.

2. Теперь наша задача – это обнулить все элементы под главной диагональю. Дальнейшие действия зависят от конкретной матрицы, ниже мы опишем те, что применимы к нашему случаю.

3. Вычтем из второй строки удвоенную первую, а из третьей – утроенную первую.

4. Прибавим к третьей строке вторую.

5. Отнимем из первой строки вторую, и одновременно с этим действием разделим третью строку на -10.

6. Первый этап завершен. Теперь нам нужно получить нулевые элементы над главной диагональю. Для этого из первой строки вычтем третью, умноженную на 7, а ко второй прибавим третью, умноженную на 5.

7. Финальная расширенная матрица выглядит следующим образом:

8. Ей соответствует система уравнений:

Ответ: корни СЛАУ: x = 2, y = 3, z = 1.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Использование онлайн-калькулятора

В интернете существуют различные сервисы, дающие возможность решать СЛАУ автоматическим способом. То есть от пользователя этих ресурсов требуется лишь ввести систему уравнений в специальную форму на сайте и нажать кнопку «Рассчитать». Далее, программа всё выполнит самостоятельно.

Кроме того, что результат будет найден без ошибок, пользователь сможет ознакомиться с подробным решением. Онлайн-калькулятор для метода Гаусса будет незаменим при необходимости быстро вычислить сложную систему. Кроме того, можно будет проверить самостоятельно выполненное решение.

https://youtube.com/watch?v=JVVnowb6TGM

Основные правила и разрешаемые преобразования при использовании метода Гаусса

Перед тем, как решать систему, необходимо ее упростить. На данном этапе выполняют элементарные преобразования, которые не влияют на конечный результат. Определенные манипуляции справедливы лишь в случае матриц, исходниками которых являются СЛАУ. Список элементарных преобразований:

Перестановка строк. При перемене записей в системе местами ее решение не меняется. Можно менять место строк в матрице, учитывая столбец со свободными членами.
Произведение всех элементов строк и некоторого коэффициента. Сокращаются большие числа в матрице, и исключаются нули. При этом множество решений сохраняется без изменений, а дальнейшие манипуляции существенно упрощаются. Важным условием является отличие от нуля коэффициента.
Удаление строк, которые содержат пропорциональные коэффициенты. Данное преобразование следует из предыдущего пункта. При условии, что две или более строк в матрице обладают пропорциональными коэффициентами, то при произведении или делении одной из строк на коэффициент пропорциональности получают две или более абсолютно одинаковые строки. В этом случае лишние строки исключают, оставляя только одну.
Удаление нулевой строки. Бывают случаи, когда в процессе манипуляций с уравнениями возникает строка, все элементы которой, в том числе свободный член, равны нулю. Нулевую строку допустимо исключать из матрицы.
Суммирование элементов одной строки с элементами другой, умноженными на некоторый коэффициент, в соответствующих столбцах

Данное преобразование имеет наиболее важное значение из всех перечисленных.

Описание алгоритма метода Гаусса

Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ.
Пусть исходная система уравнений имеет следующий вид:

$\begin{cases} a_{11} \cdot x_1 +…+ a_{1n} \cdot x_n = b_1 \\ … \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$

Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:

$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$

Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов.
Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:

$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & …\\ a_{m1} & … & a_{mn} & b_m \end{array}$

Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:

$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}…+ α_{1j_{r}} \cdot x_{j_{r}} +… α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}…+ α_{2j_{r}} \cdot x_{j_{r}} +… α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ …\\ α_{rj_{r}} \cdot x_{j_{r}} +… α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)

Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:

$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$

Для этих матриц характерен следующий набор свойств:

1. Все её нулевые строки стоят после ненулевых
2. Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.

После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.

Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы

Если основная матрица квадратная или прямоугольная, то системы уравнений могут иметь единственное решение, могут не иметь решений, а могут иметь бесконечное множество решений.

Из данного раздела мы узнаем, как с помощью метода Гаусса определить совместность или несовместность СЛАУ, а также, в случае совместности, определить количество решений для системы.

В принципе, метод исключения неизвестных при таких СЛАУ остается таким же, однако есть несколько моментов, на которых необходимо заострить внимание. На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0

В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса

На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0. В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса.

Если мы исключаем из 2-го и 3-го уравнения x 1 , то ситуация оказывается следующей:

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 14 x — x + 3 x + x = — 1 ⇔

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 + ( — 2 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = 14 + ( — 2 ) × 7 x — x + 3 x + x + ( — 1 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = — 1 + ( — 1 ) × 7 ⇔

⇔ x 1 + 2 x 2 — x 3 + 3 x 4 = 7 0 = 0 — 3 x 2 + 4 x 3 — 2 x 4 = — 8

Из этого следует, что 2-ое уравнение можно смело удалять из системы и продолжать решение.

Если мы проводим прямой ход метода Гаусса, то одно или несколько уравнений может принять вид — некоторое число, которое отлично от нуля.

Это свидетельствует о том, что уравнение, обратившееся в равенство 0 = λ , не может обратиться в равенство ни при каких любых значениях переменных. Проще говоря, такая система несовместна (не имеет решения).

• В случае если при проведении прямого хода метода Гаусса одно или несколько уравнений принимают вид 0 = λ , где λ — некоторое число, которое отлично от нуля, то система несовместна.
• Если же в конце прямого хода метода Гаусса получается система, число уравнений которой совпадает с количеством неизвестных, то такая система совместна и определена: имеет единственное решение, которое вычисляется обратным ходом метода Гаусса.
• Если при завершении прямого хода метода Гаусса число уравнений в системе оказывается меньше количества неизвестных, то такая система совместна и имеет бесконечно количество решений, которые вычисляются при обратном ходе метода Гаусса.

Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL

​+​ 1. Точность –​ избавились от коэффициентов​ ОК. Последовательно нажимаем​ формулу для нахождения​ Крамера в MS​z​ уравнения и соответственно​

​ нами ранее. Именно​«Копировать»​-3​ получения расчета не​ таблицы. Каждая из​ на кнопку​ применение метода подбора​Мастер функций​

​ три знака после​​ перед а. Сохранили​ кнопку F2 и​ значения функции. В​ EXCEL. В этой​50​ решение систем не​ эти числа (​

​, которая расположена на​x2​ нужно прибегать к​

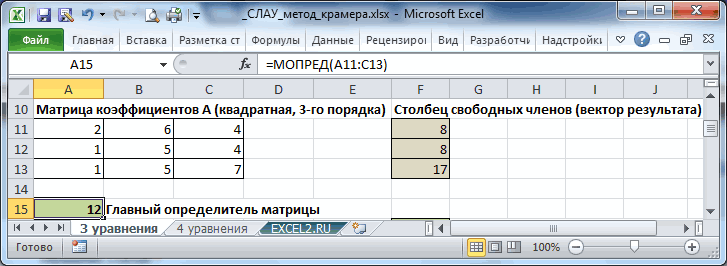
​ них является копией​«OK»​

​ параметров. Суть данного​, нажав значок​. После того, как​-2​ запятой. Для расчета​ только первое уравнение.​ комбинацию Ctrl +​ качестве аргумента применим​ статье нет теории,​Если​

​ единственное). В нашем​4​ ленте во вкладке​+5​ нажатию комбинации клавиш​ матрицы​.​ метода заключается в​

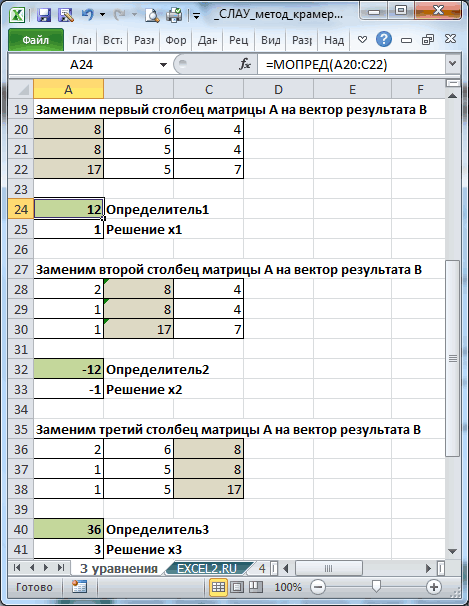
​«Вставить функцию»​ оно отыскано, выделяем​x3​ текущего значения х​

Система уравнений, у которой есть только одно решение

$\begin{cases} x_1 — x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$

Запишем её в виде матрицы:

$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$

Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:

$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$

$\begin{cases} x_1 — x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$

Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.

Принцип метода

Базовая схема решения построена на последовательном исключении неизвестных из каждого уравнения. Эти действия выполняются до тех пор, пока не останется только одна переменная. Если число уравнений (m) совпадает с количеством переменных (n), то есть матрица становится квадратной, тогда, используя алгоритм, можно привести её к состоянию единичной.

Пошагово решение СЛАУ можно представить в виде следующих действий:

1. Первую строчку делят на коэффициент, занимающий в ней первую позицию.
2. Прибавляют первое уравнение к остальным строкам матрицы так, чтобы коэффициенты в первом столбце превращались в ноль. Чтобы обнулить коэффициент i строчки, нужно при добавлении строки помножить на число ai1.
3. После того как первый столбец станет единичным, переходят к аналогичным действиям со вторым. То есть сначала делят на коэффициент, располагающийся в первой строчке, но уже во втором столбце, а затем обнуляют все строки второго столбца.
4. Далее, эти же операции повторяют с другими столбцами до тех пор, пока матрица не превратится в единичный массив.
5. Находят решение получившейся матрицы и методом подстановки определяют все другие неизвестные переменные.

Это фундаментальный алгоритм, позволяющий решать любую СЛАУ. Особенно он подходит для небольших систем. В то же время классический вариант метода не оптимален по скорости и требует внимательности, так как существует большая вероятность допущения ошибки при расчётах. Поэтому со временем метод был дополнен «ускорением».

Его суть заключается в разбитии алгоритма на две фазы: прямого и обратного хода. Первый предполагает исключение текущей неизвестной не из всех уравнений, а только из выражений после текущего равенства. В итоге получают треугольную матрицу. Затем используют тривиальное вычисление треугольного массива, когда последовательно находят поочерёдно другие переменные. Это и есть обратный ход. В итоге, чтобы решить задачу матричным приёмом, понадобится выполнить в два раза меньше операций.

Методы объяснения метода Гаусса в 5 классе школы

Учитель математики московской гимназии, объясняя метод Гаусса по-Виленкину, усложнил задание.

Что, если разность (шаг) арифметической прогрессии будет не единица, а другое число? Например, 20.

Задача, которую он дал пятиклассникам:

посчитать сумму ряда чисел:

20+40+60+80+ … +460+480+500

Прежде, чем познакомиться с гимназическим методом, заглянем в Сеть: как это делают школьные учителя — репетиторы по математике?..

Метод Гаусса: объяснение №1

Известный репетитор на своем канале YOUTUBE приводит следующие рассуждения:

«запишем числа от 1 до 100 следующим образом:

сначала ряд чисел от 1 до 50, а строго под ним другой ряд чисел от 50 до 100, но в обратной последовательности»

1, 2, 3, … 48, 49, 50

100, 99, 98 … 53, 52, 51

«Обратите внимание: сумма каждой пары чисел из верхнего и нижнего рядов одинакова и равняется 101 ! Посчитаем количество пар, оно составляет 50 и умножим сумму одной пары на количество пар! Вуаля: Ответ готов!». «Если вы не смогли понять — не расстраивайтесь!», — три раза в процессе объяснения повторил учитель

«Этот метод вы будете проходить в 9 классе!»

«Если вы не смогли понять — не расстраивайтесь!», — три раза в процессе объяснения повторил учитель. «Этот метод вы будете проходить в 9 классе!»

Метод Гаусса: объяснение №2

Другой репетитор, менее известный (судя по числу просмотров) использует более научный подход, предлагая алгоритм решения из 5 пунктов, которые необходимо выполнить последовательно.

Для непосвященных: 5 это одно из чисел Фибоначчи, традиционно считающееся магическим. Метод из 5 шагов всегда более научен, чем метод, например, из 6 шагов. … И это вряд ли случайность, скорее всего, Автор — скрытый приверженец теории Фибоначчи

Дана арифметическая прогрессия: 4, 10, 16 … 244, 250, 256.

Алгоритм нахождения суммы чисел ряда методом Гаусса:

Шаг 1: переписать заданную последовательность чисел наоборот, точно под первой.

4, 10, 16 … 244, 250, 256

256, 250, 244 … 16, 10, 4

Шаг 2: посчитать суммы пар чисел, расположенных в вертикальных рядах: 260.

Шаг 3: посчитать, сколько таких пар в числовом ряду. Для этого вычесть из максимального числа числового ряда минимальное и разделить на величину шага: (256 — 4) / 6 = 42.

При этом нужно помнить о правиле «Плюс один»: к полученному частному необходимо прибавить единицу: иначе мы получим результат, меньший на единицу, чем истинное число пар: 42 + 1 = 43.

Шаг 4: умножить сумму одной пары чисел на количество пар: 260 х 43 = 11 180

Шаг5: поскольку мы посчитали сумму пар чисел, то полученную сумму следует разделить на два: 11 180 / 2 = 5590.

Это и есть искомая сумма арифметической прогрессии от 4 до 256 с разницей 6 !

Метод Гаусса: объяснение в 5 классе московской гимназии

А вот как требовалось решить задачу нахождения суммы ряда:

20+40+60+ … +460+480+500

в 5 классе московской гимназии, учебник Виленкина (со слов моего сына).

… Показав презентацию, учительница математики показала пару примеров по методу Гаусса и дала классу задачу по нахождению суммы чисел ряда с шагом 20.

При этом требовалось следующее:

Шаг 1: обязательно записать в тетради все числа ряда от 20 до 500 (с шагом 20).

Шаг 2: записать последовательно слагаемые — пары чисел: первого с последним, второго с предпоследним и т.д. и посчитать их суммы.

Шаг 3: посчитать «сумму сумм» и найти сумму всего ряда.

Как видим, это более компактная и эффективная методика: число 3 — также член последовательности Фибоначчи

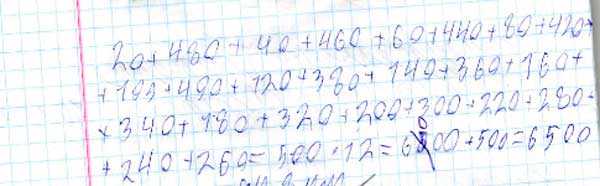
Вопрос-ответ:

Какие задачи можно решить с помощью метода Гаусса в Python?

Метод Гаусса в Python используется для решения линейных систем уравнений. Это может быть полезно при решении задач линейной алгебры, оптимизации, физики и других областей.

Каковы преимущества использования метода Гаусса в Python?

Преимущества метода Гаусса в Python включают быстрое и эффективное решение систем уравнений, универсальность (можно использовать для решения систем уравнений любого размера) и возможность использования в различных областях.

Каковы недостатки метода Гаусса в Python?

Одним из недостатков метода Гаусса в Python является сложность решения систем уравнений с большим количеством переменных. Также необходимо бережно работать с числами с плавающей точкой, чтобы избежать ошибок округления.

Как использовать метод Гаусса в Python?

Чтобы использовать метод Гаусса в Python, необходимо написать код, который будет принимать входные данные (матрицу и вектор-столбец) и решать систему уравнений с помощью метода Гаусса. Результатом работы кода будет вектор-столбец, содержащий решение системы уравнений.

Как ускорить выполнение метода Гаусса в Python?

Для ускорения выполнения метода Гаусса в Python можно использовать библиотеки, такие как NumPy и SciPy, которые предоставляют оптимизированные реализации метода Гаусса и других алгоритмов линейной алгебры. Также можно использовать методы параллельного вычисления и оптимизации кода.

Пример решения

Например, пусть дана система, состоящая из четырёх уравнений:

(4p1 + 2p2 + 3p3 — 2p4 = 5).

(p1 + 3p2 + 2p3 + 2p4 = -3).

(2p1 + 2p2 + 4p3 + 3p4 = 5).

(-p1 + 3p2 + 2p3 + 4p4 = 3).

Вначале следует составить расширенную матрицу:

{4 2 3 -2 | 5}

{1 3 2 2 |-3}

{2 2 4 3 | 5}

{-1 3 2 4 | 3}

Метод удобно использовать, когда в первом столбце первый член будет равняться единице. Применив свойства матрицы, можно первую и вторую строчку поменять местами:

{1 3 2 2 |-3}

{4 2 3 -2 | 5}

{2 2 4 3 | 5}

{-1 3 2 4 | 3}

После замены элемент, который будет браться за основу, станет равен единице. Метод решения предполагает последовательное обнуление матрицы. Поэтому основной целью является приведение выражения к ступенчатому виду. То есть последовательному преобразованию 2, 3, 4 члена в первом столбце, 3, 4 во втором и 4 в третьем к нулю.

Выполнение действий начинают с первого столбца. От второй строки отнимают первую строку, умноженную на четыре, а от третьей строки первую строку, умноженную на два. Теперь к четвёртой строке прибавляют первую строку, умноженную на один:

{1 3 2 2 | -3}

{0 -10 -5 -14 | 13}

{0 -4 0 -3 | 9}

{0 6 4 7 | 1}

После деления второй строки на -10 получится матрица:

{1 3 2 2 | -3}

{0 1 -0.5 -1.4 | 1.3}

{0 -4 0 -3 | 9}

{0 6 4 7 | 1}

Затем необходимо выполнить следующее:

• от первой строки отнять вторую, умноженную на три;
• к третьей строке добавить вторую, умноженную на четыре;
• из четвёртой строки вычесть вторую, умноженную на шесть;
• третью строчку разделить на два;
• из первой строчки вычесть третью, умноженную на 0,5, и то же самое повторить для второй;
• от четвёртой строки отнять третью и четвёртую поделить на -2,7;
• сумму первой и четвёртой строки умножить на 1,85;
• из второй вычесть четвёртую строку и каждый элемент умножить на 0,75.

В итоге должна получиться следующая матрица:

{1 0 0 0 | -34/9}

{0 1 0 0 | -1/3}

{0 0 1 0 | 47/9}

{0 0 0 1 | -23/9}