Пучок прямых.
Пучком прямых на плоскости называется множество прямых, проходящих через фиксированную точку — центр пучка. Пусть \(A_{1}x+B_{1}y+C_{1}=0\) и \(A_{2}x+B_{2}y+C_{2}=0\) — уравнения двух прямых, принадлежащих пучку. Тогда уравнение
$$
\alpha(A_{1}x+B_{1}y+C_{1})+\beta(A_{2}x+B_{2}y+C_{2})=0\label{ref13}
$$
при условии \(\alpha^{2}+\beta^{2} \neq 0\) называется уравнением пучка прямых.
Основанием для этого служит следующее утверждение.
Утверждение 3.
При любых \(\alpha\) и \(\beta\) \((\alpha^{2}+\beta^{2} \neq 0)\) уравнение \eqref{ref13} определяет прямую линию, принадлежащую пучку. Обратно, уравнение каждой прямой из пучка представимо в виде \eqref{ref13}.
Докажем сначала, что коэффициенты при переменных в уравнении \eqref{ref13} не равны нулю одновременно. Для этого перепишем его в виде
$$
(\alpha A_{1}+\beta A_{2})x+(\alpha B_{1}+\beta B_{2})y+(\alpha C_{1}+\beta C_{2})=0.\nonumber
$$
Допустим, что \(\alpha A_{1}+\beta A_{2}=0\) и \(\alpha B_{1}+\beta B_{2}=0\). Так как прямые пересекаются, \(A_{1}B_{2}-A_{2}B_{1} \neq 0\) и , что значения \(\alpha=0\), \(\beta=0\) единственные, которые удовлетворяют этим двум равенствам. Но эти значения мы исключили. Таким образом, уравнение \eqref{ref13} определяет прямую линию.
Обозначим через \(x_{0}\), \(y_{0}\) координаты центра пучка. По условию
$$
A_{1}x_{0}+B_{1}y_{0}+C_{1}=0,\ A_{2}x_{0}+B_{2}y_{0}+C_{2}=0,\nonumber
$$
а потому \(x_{0}\), \(y_{0}\) удовлетворяют уравнению \eqref{ref13}, и прямая проходит через центр пучка.
Вторая часть предложения будет доказана, если окажется, что через любую точку, отличную от центра пучка \(M_{0}\), проходит прямая линия с уравнением вида \eqref{ref13}. Легко проверить, так ли это. Рассмотрим точку \(M_{1}(x_{1}, y_{1})\), отличную от \(M_{0}\), и обозначим
$$
u=A_{1}x_{1}+B_{1}y_{1}+C_{1}=0,\ v=A_{2}x_{1}+B_{2}y_{1}+C_{2}=0\nonumber
$$
Так как наши прямые имеют только одну общую точку, числа \(u\) и \(v\) одновременно не равны нулю, и мы вправе положить \(\alpha=-v\), \(\beta=-u\). При таких значениях \(\alpha\) и \(\beta\) координаты точки \(M_{1}\) удовлетворяют уравнению \eqref{ref13}. Это означает, что соответствующая этим значениям прямая пучка проходит через \(M_{1}\), и утверждение доказано.
Заметим, что каждая пара чисел \(\alpha\) и \(\beta\) \((\alpha^{2}+\beta^{2} \neq 0)\) определяет в пучке единственную прямую, но каждой прямой соответствуют бесконечно много пропорциональных между собой пар чисел.
Если нам известны координаты центра пучка, то уравнение пучка можно написать в виде
$$
\alpha(x-x_{0})+\beta(y-y_{0})=0,\nonumber
$$
положив, что пучок определяется прямыми \(x-x_{0}=0\) и \(y-y_{0}=0\). Впрочем, и без того очевидно, что это — уравнение произвольной прямой, проходящей через \(M_{0}\).
Систему из уравнений прямых, определяющих пучок, можно рассматривать как уравнение центра пучка. Поэтому уравнение каждой прямой пучка есть следствие этой системы. Теперь наш результат можно сформулировать так.
Утверждение 4.
Если система линейных уравнений имеет решение., то некоторое линейное уравнение является ее следствием тогда и только тогда, когда оно есть сумма уравнений системы, умноженных на какие-то числа.
Мы доказали это предложение для частного случая систем из двух уравнений с двумя неизвестными. В общем виде оно вытекает из результатов главы о системах линейных уравнений. Другими геометрическими интерпретациями этого предложения являются пучки и связки плоскостей.
Пучком плоскостей называется множество плоскостей, проходящих через фиксированную прямую — ось пучка. Уравнение пучка плоскостей имеет вид
$$
\alpha(A_{1}x+B_{1}y+C_{1}z+D_{1})+\beta(A_{2}x+B_{2}y+C_{2}z+D_{2})=0,\nonumber
$$
где \(\alpha^{2}+\beta^{2} \neq 0\), а в скобках стоят левые части уравнений двух различных плоскостей пучка.
Связкой плоскостей называется множество плоскостей, проходящих через фиксированную точку — центр связки. Уравнение связки плоскостей имеет вид
$$
\alpha(A_{1}x+B_{1}y+C_{1}z+D_{1})+\beta(A_{2}x+B_{2}y+C_{2}z+D_{2}) +\\+ \gamma(A_{3}x+B_{3}y+C_{3}z+D_{3})=0,\nonumber
$$
где \(\alpha^{2}+\beta^{2}+\gamma^{2} \neq 0\), а в скобках стоят левые части уравнений плоскостей связки, имеющих центр своей единственной общей точкой.
Нахождение угла между прямой и плоскостью.
Условия задач, в которых приходится отыскивать угол между прямой и плоскостью, достаточно разнообразны. В зависимости от исходных данных, приходится подбирать соответствующий метод решения. Часто справиться с задачей нахождения угла между прямой и плоскостью помогают признаки равенства или подобия фигур, теорема косинусов и определения синуса, косинуса и тангенса угла. Также можно найти угол между прямой и плоскостью методом координат. Остановимся на нем подробнее.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , в ней задана прямая a, которая пересекает плоскость в точке M и не перпендикулярна плоскости , и требуется найти угол между прямой a и плоскостью .
Начнем с начальных данных, от которых мы будем отталкиваться при определении угла между прямой и плоскостью методом координат.
Прямой a в заданной прямоугольной системе координат Oxyz соответствуют некоторые уравнения прямой в пространстве и направляющий вектор прямой в пространстве, а плоскости — уравнение плоскости некоторого вида и нормальный вектор плоскости. Пусть — направляющий вектор прямой a, — нормальный вектор плоскости . Итак, будем считать, что нам известны координаты направляющего вектора прямой a и координаты нормального вектора плоскости (если известны уравнения прямой a и плоскости , то координаты векторов и определяются по этим уравнениям).
Осталось получить формулу, которая позволят вычислять угол между прямой и плоскостью по известным координатам направляющего вектора прямой и нормального вектора плоскости.
Отложим векторы и от точки пересечения прямой a и плоскости . В зависимости от координат векторов и возможны четыре варианта расположения этих векторов относительно заданных прямой и плоскости. Изобразим их на чертеже.
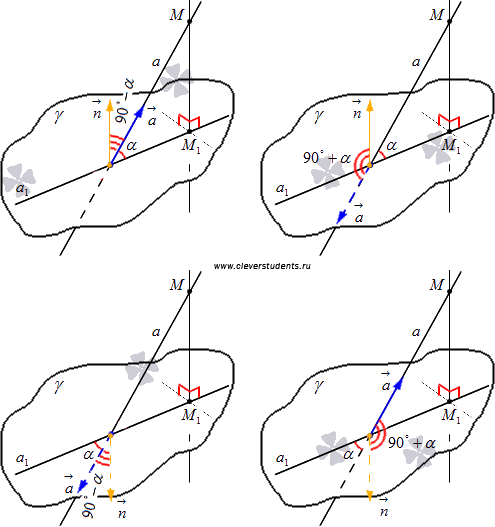
Очевидно, если и (обозначим его ) острый, то он дополняет искомый угол между прямой и плоскостью до прямого угла, то есть, . Если же , то .
Так как косинусы равных углов равны, то последние равенства можно записать следующим образом:
Формулы приведения приводят нас к равенствам , которые после преобразований принимают вид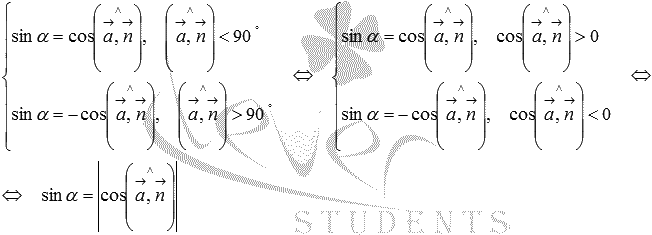
То есть, синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором плоскости.
В разделе мы выяснили, что угол между векторами равен отношению скалярного произведения векторов и произведения длин этих векторов, тогда для вычисления синуса угла между прямой и плоскостью справедлива формула 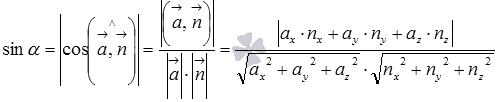 .
.
Следовательно, формула для вычисления угла между прямой и плоскостью по координатам направляющего вектора прямой и нормального вектора плоскости имеет вид 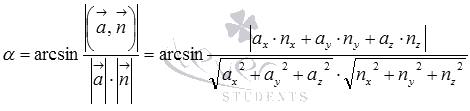 .
.
Основное тригонометрическое тождество позволяет найти косинус угла при известном синусе. Так как угол между прямой и плоскостью острый, то косинус этого угла является положительным числом и вычисляется по формуле .
Теперь мы можем находить синус угла, косинус угла и сам угол между прямой и плоскостью по полученным формулам. Решим несколько характерных примеров.
Пример.
Найдите угол, синус и косинус угла между прямой и плоскостью .
Решение.
Канонические уравнения прямой в пространстве позволяют сразу получить координаты направляющего вектора – их дают числа в знаменателях дробей. То есть, — направляющий вектор прямой .
Общее уравнение плоскости содержит в себе координаты нормального вектора плоскости в виде коэффициентов при переменных x, y и z. То есть, нормальным вектором плоскости является вектор .
Подставляем координаты векторов и в формулу для вычисления синуса угла между прямой и плоскостью: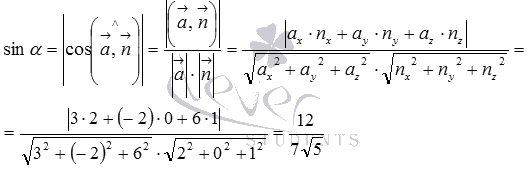
Тогда 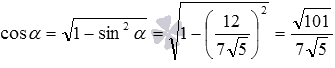 и .
и .
Ответ:
Пример.
На векторах ![]() построена пирамида. Найдите угол между прямой AD и плоскостью ABC.
построена пирамида. Найдите угол между прямой AD и плоскостью ABC.
Решение.
Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямой AD является вектор .
Нормальный вектор плоскости АВС перпендикулярен и вектору и вектору , то есть, в качестве нормального вектора плоскости АВС можно взять векторное произведение векторов и :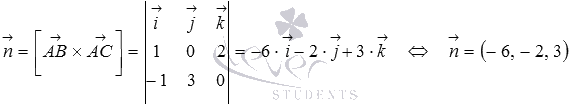
Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью: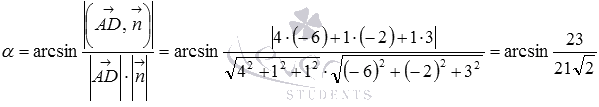
Ответ:
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
- Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
Некогда разбираться?
Примеры задач
Пример 1
Пусть нам дан параллелограмм $ABCD$ и точка $M$, не лежащая в плоскости параллелограмма. Доказать, что треугольники $AMB$ и $MBC$ являются прямоугольными, если точка $B$ — проекция точки $M$ на плоскость параллелограмма.
Доказательство.
Изобразим условие задачи на рисунке (рис. 5).
Рисунок 5.
Так как точка $B$ — проекция точки $M$ на плоскость $(ABC)$, то прямая $(MB)$ перпендикулярна плоскости $(ABC)$. По замечанию 1, получаем, что угол между прямой $(MB)$ и плоскостью $(ABC)$ равен $90^\circ$. Следовательно
\
Значит, треугольники $AMB$ и $MBC$ являются прямоугольными.
ч. т. д.
Пример 2
Дана плоскость $\alpha $. Под углом $\varphi $ к этой плоскости проведен отрезок, начало которого лежит в данной плоскости. Проекция этого отрезка в два раза меньше самого отрезка. Найти величину $\varphi $.
Решение.
Рассмотрим рисунок 6.
Рисунок 6.
По условию, имеем
\
Так как треугольник $BCD$ прямоугольный, то, по определению косинуса
\ \
Ответ: ${60}^0$.
Полупространство.
Определение.
Пусть даны плоскость \(P\) и определенный ее нормальный вектор \(\boldsymbol{n}\). Полупространством, определяемым \(P\) и \(\boldsymbol{n}\), называется множество точек \(M\) таких, что для некоторой точки \(M_{0}\) на плоскости вектор \(\overrightarrow{M_{0}M}\) составляет с \(\boldsymbol{n}\) угол, не больший \(\pi/2\).
Если \(\boldsymbol{r}\) — радиус-вектор точки \(M\), а \(\boldsymbol{r}_{0}\) — точки \(M_{0}\), то определение полупространства, эквивалентно неравенству \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\). Это неравенство и есть уравнение полупространства.
Нетрудно проверить, что определение полупространства не зависит от выбора точки \(M_{0}\). Действительно, если \(M_{1}(\boldsymbol{r}_{1})\) — другая точка плоскости, то вектор \(\boldsymbol{a}=\boldsymbol{r}_{1}-\boldsymbol{r}_{0}\) лежит в плоскости, перпендикулярен \(\boldsymbol{n}\), и мы имеем
$$
(\boldsymbol{r}-\boldsymbol{r}_{1}, \boldsymbol{n})=(\boldsymbol{r}-\boldsymbol{r}_{0}-\boldsymbol{a}, \boldsymbol{n})=(\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}).\nonumber
$$
Мы получим уравнение полупространства в координатной форме, если вспомним, что согласно утверждению 3 выражение \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})\) в координатах записывается линейным многочленом \(Ax+By+Cz+D\). Итак, полупространство в декартовой системе координат задается линейным неравенством
$$
Ax+By+Cz+D \geq 0.\nonumber
$$
Обратно, любое такое неравенство можно записать как \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\), откуда сразу видно, что оно задает полупространство.
Плоскость \(P\) и вектор \(\boldsymbol{n}_{1} =-\boldsymbol{n}\) задают другое полупространство с уравнением \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}_{1}) \geq 0\) или \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \leq 0\). Его назовем “отрицательным”, в отличие от “положительного” полупространства \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\). Однако такое наименование условно — оно определяется выбором вектора \(\boldsymbol{n}\). Изменение направления этого вектора равносильно умножению уравнения плоскости на (—1). При этом “положительное” полупространство становится “отрицательным”, и наоборот.
Вот, однако, факт, не зависящий от выбора направления нормального вектора: если \(M_{1}(x_{1}, y_{1}, z_{1})\) и \(M_{2}(x_{2}, y_{2}, z_{2})\) две точки, не лежащие в плоскости, то результаты подстановки их координат в левую часть уравнения плоскости \(Ax_{1}+By_{1}+Cz_{1}+D\) и \(Ax_{2}+By_{2}+Cz_{2}+D\) имеют один знак тогда и только тогда, когда точки лежат в одном полупространстве.
Для решения задач бывает полезно следующее замечание: если точка \(M_{0}(x_{0}, y_{0}, z_{0})\) лежит на плоскости, то точка с координатами \(x_{0}+A\), \(y_{0}+B\), \(z_{0}+C\) лежит в “положительном” полупространстве. Иначе говоря, вектор с координатами \(A, B, C\) направлен в “положительное” полупространство. Это легко проверяется подстановкой.
Вполне аналогично сказанному о полупространствах мы можем определить, что такое полуплоскость, и доказать, что неравенство \(Ax+By+Cz+D \geq 0\), связывающее декартовы координаты точки на плоскости, определяет полуплоскость. Вторая полуплоскость, ограниченная прямой \(Ax+By+C=0\), задается неравенством \(Ax+By+C \leq 0\).
Точки \(M_{1}(x_{1}, y_{1})\) и \(M_{2}(x_{2}, y_{2})\) лежат по одну сторону от прямой тогда и только тогда, когда \((Ax_{1}+By_{1}+C)(Ax_{2}+By_{2}+C) > 0\).
Понятие перпендикуляра
Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.
Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:
Запомним некоторые геометрические термины. В таком построении:
- отрезок МН – это наклонная;
- отрезок НК – это проекция наклонной, или просто проекция;
- К – основание перпендикуляра;
- Н – основание наклонной.
Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).
Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.
Найти угол между прямой и плоскостью
Выберите в какой форме задано уравнение прямой:
Теория. Угол между прямой и плоскостью
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость
Если в пространстве заданы направляющий вектор прямой L
и уравнение плоскости
A x + B y + C z + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sin φ = | | A · l + B · m + C · n | |
| √ A 2 + B 2 + C 2 · √ l 2 + m 2 + n 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Различные системы координат на плоскости и в пространстве.
§ 1. Декартова система координат на плоскости
Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.
Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.
Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.
Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).
§ 2. Полярная система координат на плоскости
Для того, чтобы задать полярную систему координат на плоскости, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.
Положение точки на плоскости задаётся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.
Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ0.
Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то
x = ρ∙cosφ,
y = ρ∙sinφ.
В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.
С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..
В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.
§3. Декартова система координат в пространстве
Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
§4. Цилиндрическая система координат в пространстве
Цилиндрическая система координат в пространстве – “родственница” полярной системы координат на плоскости. Чтобы получить цилиндрическую систему надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. Т.о., координаты точки – три числа: первые два – полярные координаты проекции нашей точки на плоскость, третье – величина проекции точки на вертикальную ось.
Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:
x = ρ·cosφ,
y = ρ·sinφ,
z = z.
§5. Сферическая система координат в пространстве
Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней — точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.
Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:
x = ρ·sinθ·cosφ,
y = ρ·sinθ·sinφ,
z = ρ·cosθ.
Пример вычисления угла между прямой и плоскостью
Найти угол между прямой
| x — 4 | = | y + 2 | = — | z — 6 |
| 2 | 6 | 3 |
и плоскостью x — 2 y + 3 z + 4 = 0.
Из уравнения прямой найдем направляющий вектор прямой
Из уравнения плоскости найдем вектор нормали плоскости
Воспользовавшись формулой, найдем угол между прямой и плоскостью
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √ 2 2 + 6 2 + (-3) 2 · √ 1 2 + (-2) 2 + 3 2 |
= | 2 — 12 — 9 | √ 4 + 36 + 9 · √ 1 + 4 + 9 = |-19| √ 49 · √ 14 = 19 7√ 14
Ответ: sin φ = 19 7√ 14 .
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют , опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
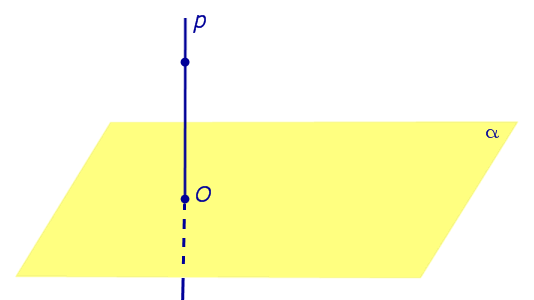
Рис.1
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия .
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
Определение 3. Прямую, пересекающую плоскость и не являющуюся , называют наклонной к этой плоскости (рис. 2).
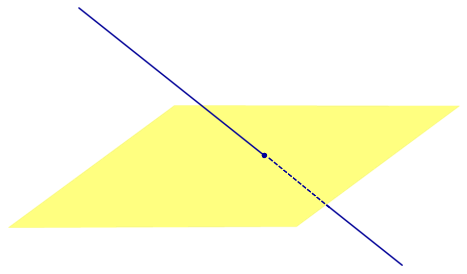
Рис.2
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
| Фигура | Рисунок | Свойство проекции |
|
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. |
||
|
На рисунке прямая PO, где P – любая точка прямой a, является α. Если прямая a параллельна плоскости α, то проекцией прямой a является прямая a’, лежащая в плоскости α, a и проходящая через основание O перпендикуляра PO. |
||
|
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a . |
||
| Прямая, перпендикулярная к плоскости |
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O, то точка O и является проекцией этой прямой на плоскость α. |
|
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. |
|
На рисунке прямая PO, где P – любая точка прямой a, является α. Если прямая a параллельна плоскости α, то проекцией прямой a является прямая a’, лежащая в плоскости α, a и проходящая через основание O перпендикуляра PO. |
|
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a . |
| Прямая, перпендикулярная к плоскости |
|
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O, то точка O и является проекцией этой прямой на плоскость α. |
Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ , проходящей через точку M , при условии, что она не принадлежит плоскости γ .
Проекция прямой а на плоскость γ — это множество проекций всех точек заданной прямой на плоскость.
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.






























