Джоуль.
Джоуль – единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ). Имеет русское обозначение – Дж и международное обозначение – J.
Другие единицы измерения
Джоуль, как единица измерения:
Джоуль – единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ), названная в честь английского физика Джеймса Прескотта Джоуля.
Джоуль как единица измерения имеет русское обозначение – Дж и международное обозначение – J.
В классической физике джоуль равен работе, совершаемой при перемещении точки приложения силы, равной 1 (одному) ньютону (Н), на расстояние одного метра в направлении действия силы.
Дж = Н · м = кг · м2 / с2.
1 Дж = 1 Н · 1 м = 1 кг · 1 м2 / 1 с2.
В электричестве джоуль означает работу, которую совершают силы электрического поля за 1 секунду при напряжении в 1 вольт (В) для поддержания силы тока в 1 ампер (А). Это энергия, которая выделится за 1 секунду при прохождении тока через проводник силой тока 1 ампер (А) при напряжении 1 вольт (В).
В Международную систему единиц джоуль введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы джоуль пишется со строчной буквы, а её обозначение – с заглавной (Дж). Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием джоуля.
В джоулях измеряют выполненную работу, энергию и количество теплоты.
Представление джоуля в других единицах измерения – формулы:
Через основные единицы системы СИ джоуль выражается следующим образом:
Дж = Н · м
Дж = кг · м2 / с2.
Дж = Вт / с.
Дж = А2 · Ом · с.
Дж = В2 · с / Ом.
Дж = Кл · В.
где А – ампер, В – вольт, Дж – джоуль, Кл – кулон, м – метр, Н – ньютон, с – секунда, Вт – ватт, кг – килограмм, Ом – ом.
Перевод в другие единицы измерения:
1 Дж ≈ 6,24151 ⋅ 1018 эВ
1 МДж = 0,277(7) кВт · ч
1 кВт · ч = 3,6 МДж
1 Дж ≈ 0,238846 калориям
1 калория (международная) = 4,1868 Дж
1 килограмм-сила-метр (кгс·м) = 9,80665 Дж
1 Дж ≈ 0,101972 кгс·м
Кратные и дольные единицы:
Кратные и дольные единицы образуются с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Дж | декаджоуль | даДж | daJ | 10−1 Дж | дециджоуль | дДж | dJ |
| 102 Дж | гектоджоуль | гДж | hJ | 10−2 Дж | сантиджоуль | сДж | cJ |
| 103 Дж | килоджоуль | кДж | kJ | 10−3 Дж | миллиджоуль | мДж | mJ |
| 106 Дж | мегаджоуль | МДж | MJ | 10−6 Дж | микроджоуль | мкДж | µJ |
| 109 Дж | гигаджоуль | ГДж | GJ | 10−9 Дж | наноджоуль | нДж | nJ |
| 1012 Дж | тераджоуль | ТДж | TJ | 10−12 Дж | пикоджоуль | пДж | pJ |
| 1015 Дж | петаджоуль | ПДж | PJ | 10−15 Дж | фемтоджоуль | фДж | fJ |
| 1018 Дж | эксаджоуль | ЭДж | EJ | 10−18 Дж | аттоджоуль | аДж | aJ |
| 1021 Дж | зеттаджоуль | ЗДж | ZJ | 10−21 Дж | зептоджоуль | зДж | zJ |
| 1024 Дж | иоттаджоуль | ИДж | YJ | 10−24 Дж | иоктоджоуль | иДж | yJ |
Интересные примеры:
Дульная энергия пули при выстреле из автомата Калашникова – 2030 Дж.
Энергия, необходимая для нагрева 1 литра воды от 20 до 100 °C, составляет 3,35⋅105 Дж.
Энергия, выделяемая при взрыве 1 тонны тринитротолуола (тротиловый эквивалент), – 4,184⋅109 Дж.
Примечание: Фото https://www.pexels.com, https://pixabay.com
карта сайта
формула энергии закон джоуля ленца можно тепловой 1 м дж джоуль ленц закон равен 2 2 равен единица теплота масса тела сила количество теплоты работа кинетическая энергия в джоулях в секунду 10 5 8 6 20 200 100 виды сколько степени джоулейкилоджоули скорость в джоули в кг килограммы 3 4 джоуля
Коэффициент востребованности
3 492
Температура
В определенных областях, таких как физика плазмы , удобно использовать электронвольт для выражения температуры. Электронвольт делится на постоянную Больцмана для преобразования в шкалу Кельвина :
- 1kBзнак равно1,602 176 634×10-19 Дж / эВ1,380 649×10-23 Дж / Кзнак равно11 604,518 12 К / эВ.{\ displaystyle {1 \ over k _ {\ text {B}}} = {1.602 \ 176 \ 634 \ times 10 ^ {- 19} {\ text {J / eV}} \ over 1.380 \ 649 \ times 10 ^ { -23} {\ text {J / K}}} = 11 \ 604.518 \ 12 {\ text {K / эВ}}.}
Где k B — постоянная Больцмана , K — Кельвин, J — Джоули, eV — электронвольты.
Предполагается, что k B используется для выражения температуры с помощью электронвольт, например, типичная термоядерная плазма с магнитным удержанием имеет вид15 кэВ ( килоэлектронвольт ), что равно 170 МК (миллион Кельвинов).
В качестве приближения: k B T составляет около0,025 эВ (≈290 К11604 К / эВ) при температуре 20 ° С .
Энергия электрического поля конденсатора
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:
Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.
Плотность энергии электрического поля:
где \( V \) – объем пространства между обкладками конденсатора.
Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.
Примечания и ссылки
Заметки
- Потенциал извлечения элемента относится к измерению энергии когезии, характерной для простых минеральных тел с кристаллической или поликристаллической структурой. Атомы, группы или атомные плоскости могут быть оторваны во время УФ-спектрометрических измерений в вакууме. Нормальные электродные потенциалы, например в водном растворе при 298 К , в электрохимии эквивалентны электродвижущим силам клетки или напряжениям, характерным для окислительно-восстановительных реакций, выраженным в вольтах. Однако англосаксонская традиция приравнивает их к энергии, выраженной в эВ.
Рекомендации
- Международное бюро мер и весов , Международная система единиц (СИ) , Севр, BIPM,2019 г., 9- е изд. , 216 с. , гл. 4 («Единицы вне ИС, использование которых разрешено ИС»), стр. 33.
- Р. Тайле, Л. Виллен и П. Февр, Физический словарь , De Boeck Supérieur,2018 г. , стр. 454 (таблица 32).
Потенциальность электростатического поля
Электрическое поле с напряженностью \( \vec{E} \) при перемещении заряда \( q \) совершает работу. Работа \( A \) электростатического поля вычисляется по формуле:
где \( d \) – расстояние, на которое перемещается заряд,
\( \alpha \) – угол между векторами напряженности электрического поля и перемещения заряда.
Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.
Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.
Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным
Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой \( W \), так как буквой \( E \) обозначают напряженность поля:
Потенциальная энергия заряда \( q \), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.
Проводники в электрическом поле
Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.
Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.
Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.
Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.
Важно!Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей
На этом основана электростатическая защита.
Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.
Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.
Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны)
Основные сведения
В физике элементарных частиц в электронвольтах обычно выражается не только энергия Е, но и масса m элементарных частиц. Основанием для этого служит тот факт, что в силу эквивалентности массы и энергии выполняется соотношение m = E0/c2, где c — скорость света, E0 — энергия покоящейся частицы. Поскольку c — фундаментальная постоянная, равная 299 792 458 м/с (точно), не изменяющаяся ни при каких условиях, то указание в качестве характеристики массы частицы её энергии покоя, выраженной в электронвольтах, однозначно определяет значение массы в любых традиционных единицах и к недоразумениям не приводит. В единицах массы 1 эВ = 1,782 661 921…⋅10−36 кг (точно), и напротив, 1 кг = 5,609 588 603…⋅1035 эВ (точно). Атомная единица массы близка по значению к 1 ГэВ (с погрешностью около 7 %): 1 а. е. м. = 931,494 102 42(28) МэВ, и напротив, 1 ГэВ = 1,073 544 102 33(32) а. е. м.. Импульс элементарной частицы также может быть выражен в электронвольтах (строго говоря, в эВ/c).
Электронвольт по сравнению с энергиями, характерными для большинства ядерных процессов, — маленькая величина, в этой области физики обычно применяются кратные единицы:
- килоэлектронвольт (кэВ) — 1000 эВ,
- мегаэлектронвольт (МэВ) — 1 млн электронвольт,
- гигаэлектронвольт (ГэВ) — 1 млрд электронвольт,
- тераэлектронвольт (ТэВ) — 1 трлн электронвольт.
Последнее поколение ускорителей элементарных частиц позволяет достичь нескольких триллионов электронвольт (тераэлектронвольт, ТэВ). Один ТэВ приблизительно равен (кинетической) энергии летящего комара или энергии, выделяющейся при падении маленькой капли воды диаметром в 1 мм (массой ок. 0,5 мг) с высоты 3 см.
Температура, которая является мерой средней кинетической энергии частиц, тоже иногда выражается в электронвольтах, исходя из соотношения температуры и энергии частиц в одноатомном идеальном газе Eкин = 3⁄2kТ. В температурных единицах 1 эВ соответствует 11 604,518 12… кельвин (точно) (см. постоянная Больцмана).
В электронвольтах выражают энергию квантов электромагнитного излучения (фотонов). Энергия фотонов с частотой ν в электронвольтах численно равна hν/EэВ, а излучения с длиной волны λ — hc/(λEэВ), где h — постоянная Планка, а EэВ — энергия, равная одному электронвольту, выраженная в единицах той же системы единиц, что и использованная для выражения h, ν и λ. Так как для ультрарелятивистских частиц, в том числе фотонов, λE = hc, то при вычислении энергии фотонов с известной длиной волны (и наоборот) часто полезен коэффициент пересчёта, представляющий собой выраженное в эВ·нм произведение постоянной Планка и скорости света:
hc = 1239,841 984… эВ·нм (точно) ≈ 1240 эВ·нм.
Так, фотон с длиной волны 1 нм имеет энергию 1240 эВ; фотон с энергией 10 эВ имеет длину волны 124 нм и т. д.
В электронвольтах измеряется также работа выхода при внешнем фотоэффекте — минимальная энергия, необходимая для удаления электрона из вещества под действием света.
В химии часто используется молярный эквивалент электронвольта. Если один моль электронов или однозарядных ионов перенесён между точками с разностью потенциалов 1 В, он приобретает (или теряет) энергию Q = 96 485,332 12… Дж (точно), равную произведению 1 эВ на число Авогадро. Эта величина, выраженная в джоулях, численно равна постоянной Фарадея (модулю заряда 1 моля электронов), выраженной в кулонах. Аналогично, если при химической реакции в одном моле вещества выделяется (или поглощается) энергия 96,485 кДж, то соответственно каждая молекула теряет (или получает) около 1 эВ.
В электронвольтах измеряется также ширина распада Γ элементарных частиц и других квантовомеханических состояний, например ядерных энергетических уровней. Ширина распада — это неопределённость энергии состояния, связанная с временем жизни состояния τ соотношением неопределённостей: Γ = ħ/τ). Частица с шириной распада 1 эВ имеет время жизни 6,582 119 569…⋅10−16 с (точно). Аналогично квантовомеханическое состояние с временем жизни 1 с имеет ширину 6,582 119 569…⋅10−16 эВ (точно).
Одним из первых термин «электронвольт» применил американский физик и инженер Карл Дарроу в 1923 году.
использовать
Как единица измерения энергии
Электрон-вольт используется как «удобная» единица измерения энергии в атомной физике и смежных областях, таких как экспериментальная ядерная физика и физика элементарных частиц . Например, кинетическая энергия, до которой частица приводится в ускорителе частиц, всегда выражается в электрон-вольтах. Удобный, который, таким образом, потому что изменение кинетической энергии каждого в электрическом поле ускоренных частиц от его нагрузки и пройденного напряжение , как можно рассчитать и не зависит от других факторов: масса частицы, длина из путь или точный пространственный профиль напряженности поля не имеет значения.
ΔЭ.родственник{\ displaystyle \ Delta E _ {\ text {kin}}}Q{\ displaystyle Q}U{\ displaystyle U}ΔЭ.родственникзнак равноUQ{\ displaystyle \ Delta E _ {\ text {kin}} = UQ}
Количество заряда свободной наблюдаемой частицы всегда равно элементарному заряду или его целому кратному. Вместо использования элементарного заряда и указания энергии в джоулях изменение кинетической энергии в результате электрического ускорения может быть указано непосредственно в единицах эВ. Формула применима для однозарядных частиц, таких как электроны, протоны и однозарядные ионы ; для β-кратных заряженных частиц применяется соответственно . Например, кинетическая энергия протона изменяется на 100 эВ, когда он пролетает через разность потенциалов 100 В, энергия двухзарядного ядра гелия изменяется на 200 эВ.
е{\ displaystyle e}ΔЭ.родственникзнак равноеU{\ displaystyle \ Delta E _ {\ text {kin}} = e \, U}Z{\ displaystyle Z}ΔЭ.родственникзнак равноZеU{\ displaystyle \ Delta E _ {\ text {kin}} = Ze \, U}
Кинетическая энергия положительно заряженной частицы уменьшается на величину , указанную в , когда пройден напряжение поляризованы таким образом, что электрический потенциал на пути частицы с учетом (просторечии называется « в то время как частицы от плюс до минус ходу»); в противном случае он уменьшается. Для отрицательно заряженных частиц то же самое применимо с противоположным знаком (см., Например, ).
Использование единицы электрон-вольта не ограничивается работой по ускорению заряженных частиц в электрическом поле. Поскольку его порядок величины является благоприятным для атомной и ядерной физики, он часто используется для совершенно разных энергий в микроскопическом масштабе, например, для энергий связи в атомной оболочке или в атомном ядре или для энергии отдельных фотоны .
Как единица массы в физике элементарных частиц
Электрон-вольт также можно использовать как единицу массы частиц. Преобразование массы в энергию осуществляется в соответствии с эквивалентностью массы и энергии . Эта энергия называется энергией покоя .
- Э.знак равномc2⇔мзнак равноЭ.c2{\ Displaystyle E = mc ^ {2} \ quad \ Leftrightarrow \ quad m = {\ dfrac {E} {c ^ {2}}}},
в котором
- Э.{\ displaystyle E} для энергии
- м{\ displaystyle m} для толпы и
- c{\ displaystyle c}обозначает скорость света .
Таким образом, соответствующая единица массы — . Перевод в килограммах:
еVc2{\ Displaystyle \ mathrm {эВ} / с ^ {2}}
- 1еVc2≈1,783⋅10-36kг{\ Displaystyle 1 \, \ mathrm {eV} / c ^ {2} \ приблизительно 1 {,} 783 \ cdot 10 ^ {- 36} \, \ mathrm {кг}}.
Например, масса электрона 9,11 · 10 −31 кг = 511 кэВ / c².
Система «естественных» единиц часто используется в физике элементарных частиц . Это установлено. Таким образом, масса частицы равна ее кинетической энергии. Оба значения обычно выражаются в электрон-вольтах.
cзнак равно1{\ displaystyle c = 1}
Мощность в спорте
Оценивать работу с помощью мощности можно не только для машин, но и для людей и животных. Например, мощность, с которой баскетболистка бросает мяч, вычисляется с помощью измерения силы, которую она прикладывает к мячу, расстояния которое пролетел мяч, и времени, в течение которого эта сила была применена. Существуют сайты, позволяющие вычислить работу и мощность во время физических упражнений. Пользователь выбирает вид упражнений, вводит рост, вес, длительность упражнений, после чего программа рассчитывает мощность. Например, согласно одному из таких калькуляторов, мощность человека ростом 170 сантиметров и весом в 70 килограмм, который сделал 50 отжиманий за 10 минут, равна 39.5 ватта. Спортсмены иногда используют устройства для определения мощности, с которой работают мышцы во время физической нагрузки. Такая информация помогает определить, насколько эффективна выбранная ими программа упражнений.
Динамометры
Для измерения мощности используют специальные устройства — динамометры. Ими также можно измерять вращающий момент и силу. Динамометры используют в разных отраслях промышленности, от техники до медицины. К примеру, с их помощью можно определить мощность автомобильного двигателя. Для измерения мощности автомобилей используется несколько основных видов динамометров. Для того, чтобы определить мощность двигателя с помощью одних динамометров, необходимо извлечь двигатель из машины и присоединить его к динамометру. В других динамометрах усилие для измерения передается непосредственно с колеса автомобиля. В этом случае двигатель автомобиля через трансмиссию приводит в движение колеса, которые, в свою очередь, вращают валики динамометра, измеряющего мощность двигателя при различных дорожных условиях.
Динамометры также используют в спорте и в медицине. Самый распространенный вид динамометров для этих целей — изокинетический. Обычно это спортивный тренажер с датчиками, подключенный к компьютеру. Эти датчики измеряют силу и мощность всего тела или отдельных групп мышц. Динамометр можно запрограммировать выдавать сигналы и предупреждения если мощность превысила определенное значение
Это особенно важно людям с травмами во время реабилитационного периода, когда необходимо не перегружать организм
Согласно некоторым положениям теории спорта, наибольшее спортивное развитие происходит при определенной нагрузке, индивидуальной для каждого спортсмена. Если нагрузка недостаточно тяжелая, спортсмен привыкает к ней и не развивает свои способности. Если, наоборот, она слишком тяжелая, то результаты ухудшаются из-за перегрузки организма. Физическая нагрузка во время некоторых упражнений, таких как велосипедный спорт или плавание, зависит от многих факторов окружающей среды, таких как состояние дороги или ветер. Такую нагрузку трудно измерить, однако можно выяснить с какой мощностью организм противодействует этой нагрузке, после чего изменять схему упражнений, в зависимости от желаемой нагрузки.
Автор статьи: Kateryna Yuri
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:
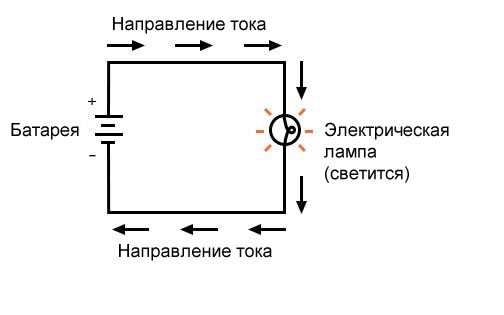Рисунок 1 – Пример простой схемы
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
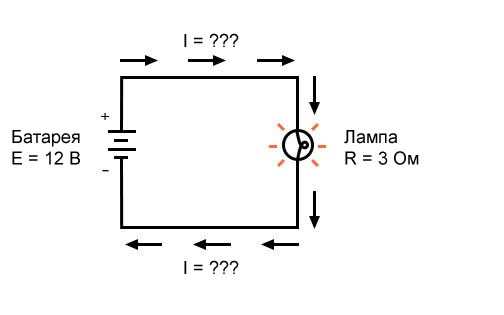Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы
Какая величина тока (I) в этой цепи?
\
Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
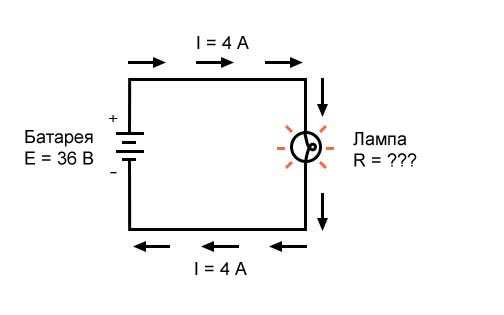Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи
Какое сопротивление (R) оказывает лампа?
\
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
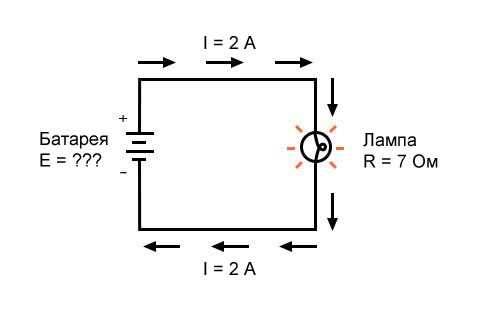Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы
Какое напряжение обеспечивает батарея?
\
Примеры задач
Задача №1
При нормальном режиме работы тостера сила тока в его электрической цепи равна $6 \space А$. Напряжение в сети составляет $220 \space В$. Найдите работу электрического тока в цепи за $5 \space мин$.
Дано:$t = 5 \space мин$$I = 6 \space А$$U = 220 \space В$
СИ:$t = 300 \space с$
$A — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для определения напряжения и выразим из нее работу:$U = \frac{A}{q}$,$A = Uq$.
Как найти электрический заряд? Запишем формулу для расчет силы тока и выразим заряд из нее:$I = \frac{q}{t}$,$q = It$.
Подставим это в формулу для расчета работы электрического тока:$A = Uq = UIt$.
Рассчитаем эту величину:
$A = 220 \space В \cdot 6 \space А \cdot 300 \space с = 396 \space 000 \space Дж = 396 \space кДж$.
Ответ: $A = 396 \space кДж$.
Задача №2
На рисунке 5 представлены графики зависимости работы электрического поля (тока) $A$ от перемещаемого заряда $q$ по двум проводникам. Используя график, вычислите напряжение между концами каждого проводника.
Рисунок 5. Графики зависимости работы тока от перемещаемого заряда по двум проводникам
На графике выберем удобные для нас точки с точными значениями заряда и работы. Для графика $I$ выберем точку со значениями $q = 0.35 \space Кл$ и $A = 70 \space Дж$. Для графика $II$: $q = 0.35 \space Кл$ и $A = 40 \space Дж$. Запишем условие задачи и решим ее.
Дано:$q_1 = q_2 = 0.35 \space Кл$$A_1 = 70 \space Дж$$A_2 = 40 \space Дж$
$U_1 — ?$$U_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитывать напряжения для данных проводников будем по формуле $U = \frac{A}{q}$.
$U_1 = \frac{A_1}{q_1} = \frac{70 \space Дж}{0.35 \space Кл} = 200 \space В$.
$U_2 = \frac{A_2}{q_2} = \frac{40 \space Дж}{0.35 \space Кл} \approx 114 \space В$.
Ответ: $U_1 = 200 \space В$, $U_2 \approx 114 \space В$.
Взаимодействие зарядов. Два вида зарядов
Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.
Обозначение – \( q \), единица измерения в СИ – кулон (Кл).
Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10-19 Кл), наименьший положительный заряд (1,6·10-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.
Величина заряда тела будет равна
где \( N \) — число избыточных или недостающих электронов;
\( e \) — элементарный заряд, равный 1,6·10-19 Кл.
Важно!
Частица может не иметь заряда, но заряд без частицы не существует. Электрические заряды взаимодействуют:
Электрические заряды взаимодействуют:
заряды одного знака отталкиваются:
заряды противоположных знаков притягиваются:
Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.
Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Расстояние
В физике элементарных частиц , система «естественных единиц» , в которой скорость света в вакууме с , и приведенная постоянная Планка ħ безразмерные и равным единице широко используется: с = ħ = 1 . В этих единицах и расстояния, и время выражаются в единицах обратной энергии (в то время как энергия и масса выражаются в одних и тех же единицах, см. Эквивалентность массы и энергии ). В частности, длины рассеяния частиц часто выражаются в единицах обратной массы частиц.
Вне этой системы единиц коэффициенты преобразования электронвольт, секунды и нанометра следующие:
- ℏзнак равночас2πзнак равно1.054 571 817 646×10-34 J sзнак равно6,582 119 569 509×10-16 эВ с.{\ displaystyle \ hbar = {{h} \ over {2 \ pi}} = 1.054 \ 571 \ 817 \ 646 \ times 10 ^ {- 34} \ {\ mbox {J s}} = 6.582 \ 119 \ 569 \ 509 \ times 10 ^ {- 16} \ {\ mbox {эВ с}}.}
Приведенные выше соотношения также позволяют выразить среднее время жизни τ нестабильной частицы (в секундах) через ширину ее распада Γ (в эВ) через Γ = ħ / τ . Например, мезон B имеет время жизни 1,530 (9) пикосекунд , средняя длина распада cτ =459,7 мкм или шириной распада(4.302 ± 25) × 10 −4 эВ .
И наоборот, крошечные разности масс мезонов, ответственные за колебания мезонов , часто выражаются в более удобных обратных пикосекундах.
Энергия в электронвольтах иногда выражается через длину волны света с фотонами той же энергии:
- 1эВчасcзнак равно(1,602 176 634×10-19J)(2,99 792 458×1010смs)⋅(6,62 607 015×10-34J⋅s)≈8065.5439см-1.{\ displaystyle {\ frac {1 \; {\ text {eV}}} {hc}} = {\ frac {(1.602 \ 176 \ 634 \ times 10 ^ {- 19} \; {\ text {J}}) )} {(2,99 \ 792 \ 458 \ times 10 ^ {10} \; {\ text {cm}} / {\ text {s}}) \ cdot (6,62 \ 607 \ 015 \ times 10 ^ {- 34} \; {\ text {J}} \ cdot {\ text {s}})}} \ Thickapprox 8065.5439 \; {\ text {cm}} ^ {- 1}.}
Расстояние
В физика элементарных частиц, система «естественных единиц», в которой скорость света в вакууме c и приведенная постоянная Планка час безразмерны и равны единице. c = час = 1. В этих единицах и расстояния, и время выражаются в единицах обратной энергии (в то время как энергия и масса выражаются в тех же единицах, см. эквивалентность массы и энергии ). В частности, частица длины рассеяния часто выражаются в единицах обратной массы частиц.
Вне этой системы единиц коэффициенты преобразования электронвольт, секунды и нанометра следующие:
- ℏ=час2π=1.054 571 817 646×10−34 J s=6.582 119 569 509×10−16 эВ с.{displaystyle hbar = {{h} over {2pi}} = 1.054 571 817 646 imes 10 ^ {- 34} {mbox {J s}} = 6.582 119 569 509 imes 10 ^ {- 16} {mbox {eV s} }.}
Приведенные выше соотношения также позволяют выразить средняя продолжительность жизни τ нестабильной частицы (в секундах) с точки зрения ее ширина распада Γ (в эВ) через Γ = час/τ. Например, B мезон имеет срок службы 1,530 (9)пикосекунды, средняя длина распада cτ = 459,7 мкм, или ширина спада (4.302±25)×10−4 эВ.
И наоборот, крошечные различия масс мезонов, ответственные за мезонные колебания часто выражаются в более удобных обратных пикосекундах.
Энергия в электронвольтах иногда выражается через длину волны света с фотонами той же энергии:
- 1эВчасc=(1.602 176 634×10−19J)(2.99 792 458×1010смs)⋅(6.62 607 015×10−34J⋅s)≈8065.5439см−1.{displaystyle {frac {1; {ext {eV}}} {hc}} = {frac {(1.602 176 634 imes 10 ^ {- 19}; {ext {J}})} {(2.99 792 458 imes 10 ^ {10}; {ext {cm}} / {ext {s}}) cdot (6.62 607 015 imes 10 ^ {- 34}; {ext {J}} cdot {ext {s}})}} hickapprox 8065.5439; {ext {cm}} ^ {- 1}.}
Закон Кулона
Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.
Закон Кулона формулируется так:
сила взаимодействия \( F \) двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям \( q_1 \) и \( q_2 \) и обратно пропорциональна квадрату расстояния между ними \( r \):
где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м2)/Кл2 – коэффициент пропорциональности,
\( \varepsilon_0=8.85\cdot10^{-12} \) Кл2/(Н·м2) – электрическая постоянная.
Коэффициент \( k \) численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.
Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.
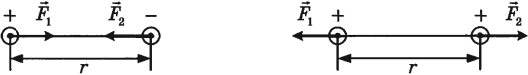
Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:
где \( \varepsilon \) – диэлектрическая проницаемость среды.
Закон Кулона применим к взаимодействию
- неподвижных точечных зарядов;
- равномерно заряженных тел сферической формы.
В этом случае \( r \) – расстояние между центрами сферических поверхностей.
Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции)