Примеры и задачи
Пример 1 Расчет:
1) 15 – 5 – 3;
2) 16 — 6 — 1;
3) 18 – 8 – 9.
Решение:
1) 15 — 5 — 3 = 10 — 3 = 7;
2) 16 — 6 — 1 = 10 — 1 = 9;
3) 18 — 8 — 9 = 10 — 9 = 1.
Пример 2 Расчет:
1) 11-7;
2) 17-9;
3) 14 — 5.
Решение:
1) 11 — 7 = 11 — 1 — 6 = 10 — 6 = 4;
2) 17 — 9 = 17 — 7 — 2 = 10 — 2 = 8;
3) 14 — 5 = 14 — 4 — 1 = 10 — 1 = 9.
Упражнение 1. У Маши было 16 рублей. Она купила карандаш за 7 рублей и конфету за 8 рублей. Сколько денег осталось у Маши?
Решение:
16 — 7 = 9 — количество рублей, оставшееся после покупки карандаша;
9 — 8 = 1 — количество рублей, оставшееся после покупки конфеты.
Ответ: 1 рубль.
Задача 2. В одной коробке было 13 конфет, а в другой — 9 конфет меньшего размера. Сколько конфет было в двух коробках?
Решение: Сначала найдите, сколько конфет во второй коробке:
13 — 9 = 4.
Теперь найдем общее количество конфет, прибавив количество конфет в первой коробке к количеству конфет во второй коробке:
13 + 4 = 17.
Ответ: 17 конфет.
Вычитание единиц из произвольных натуральных чисел.
Будем считать, что уменьшаемое является многозначным натуральным числом, которое можно представить в виде суммы разрядных слагаемых (другие случаи мы рассмотрели в предыдущем пункте и при изучении вычитания с помощью таблицы сложения). Чтобы вычесть из такого натурального числа однозначное натуральное число, нужно уменьшаемое разложить по разрядам, после чего выполнить вычитание числа из суммы.
Рассмотрим решения нескольких примеров.
Вычислим разность чисел 46 и 2. Число 46 раскладывается по разрядам в сумму 40+6, тогда 46−2=(40+6)−2=40+(6−2)=40+4=44.
Усложним пример. Вычтем из 46 число 8. Имеем 46−8=(40+6)−8. Так как 8 больше, чем 6, то в этом случае: (40+6)−8=(40−8)+6. Разность 40−8 вычислим так, как мы это делали в предыдущем пункте: 40−8=(30+10)−8=30+(10−8)=30+2=32. Тогда (40−8)+6=32+6=38.
Теперь отнимем от числа 6 047 число 5. Раскладываем по разрядам число 6 047 и вычитаем число из суммы: 6 047−5=(6 000+40+7)−5=6 000+40+(7−5)=6 000+40+2=6 042.
Для закрепления навыков разберем решение еще одного примера.
Вычтем из числа 2 503 число 8. Раскладываем уменьшаемое по разрядам, при этом получаем 2 503−8=(2 000+500+3)−8. Так как 8 больше, чем 3, но меньше, чем 500, то справедливо равенство (2 000+500+3)−8=2 000+(500−8)+3.
Вычислим разность 500−8, для этого представляем число 500 в виде суммы 400+100=400+90+10 (при необходимости вернитесь к предыдущему пункту этой статьи) и выполняем необходимые вычисления:500−8=(400+90+10)−8=400+90+(10−8)=400+90+2=492.
Осталось закончить вычисления: 2 000+(500−8)+3=2 000+492+3=2 495.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Эта сложная наука – математика
Некоторым деткам научиться математическому счету бывает намного труднее, чем, например, научиться читать. Поэтому, чтобы у ребенка появилась так называемая «симпатия» к предмету, родителям придется постараться привить любовь ребенка к математике.
Некоторые родители не желают обременять себя подобными делами и перекладывают обучение вычислениям на плечи педагогов начальной школы. Безусловно, именно учителя и выполняют обучение счету детей, но родители не должны самоустраняться, а обязаны помогать ребенку, помогать находить ошибки, анализировать их.
Даже если вы решили воспользоваться услугами репетитора, заниматься с ребенком дома все равно придется, ведь учитель задает домашние задания, которые следует добросовестно выполнять. В противном случае знания, не подкрепленные практикой, очень быстро забудутся.
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Приемы сложения и вычитания вида□ + 4, □–4
А в нашей сказке появился новый герой. Это хитрая лисичка. Увидела она теремок, а в нем мышку, лягушку и зайчика.
Попросилась лисичка к ним жить. А зверята согласились ее пустить только если она поможет им составить математические таблицы. Лисичка очень хитрая была и быстро придумала, как выполнить их задание.
У лисички всего 4 лапки. Она посчитала, что у нее 2 передние и 2 задние лапки. Значит четыре это два и два.
Вспомни, кто нам помогал составлять таблицы числа 2.
Правильно. Это лягушка-квакушка, перепрыгивая через число, может быстро найти ответ для любого примера из этой таблицы. А чтобы прибавить 4, лягушке нужно прыгнуть дважды.
Лисичка попросила ее стать на число 1 и прыгнуть вперед один раз, а потом еще раз.
Вот и решен пример. Посмотри, где оказалась лягушка.
Значит 1 + 4 = 5.
Оказалось, что решать примеры в таблице сложения с числом 4 очень легко. Лягушка-квакушка продолжала дважды перепрыгивать через число, а ее друзья записали всю таблицу.
Быстро справившись с этим заданием, зверята сами догадались, что для составления таблицы вычитания числа 4 лягушке придется прыгать дважды в обратном направлении.
Вот посмотри, как они решили первый пример из этой таблицы.
Откуда начала прыгать лягушка? Какой результат получился? Как запишем?
5 − 4 = 1
Так и остальную таблицу составили.
Если ты уже запомнил таблицы для числа 2, то и эту таблицу выучишь очень легко.
Табличное сложение
Прежде чем познакомиться с таблицами сложения чисел, мы рассмотрим случаи сложения разных видов.
Например, 7 + 6 = ?
Мы видим, что сумма будет больше 10, потому что 10 — это 7 и 3. Мы будем прибавлять число 6 по частям.
- Сначала прибавляем столько, чтобы получить 10: 7 + 3 = 10.
- Дальше мы вспоминаем, что 6 — это 3 и 3.
- Число 3 мы уже прибавили, значит, надо прибавить ещё 3: 10 + 3 = 13.
- Тогда наш пример 7 + 6 можно записать по-другому:
или так:
Значит, 7 + 6 = 13
Рассуждая так, можно решить любой пример на сложение в пределах 20.
Случаи табличного сложения
- 11 — это 1 и 10
- 11 — это 2 и 9
- 11 — это 3 и 8
- 11 — это 4 и 7
- 11 — это 5 и 6
- 12 — это 2 и 10
- 12 — это 3 и 9
- 12 — это 4 и 8
- 12 — это 5 и 7
- 12 — это 6 и 6
- 13 — это 3 и 10
- 13 — это 4 и 9
- 13 — это 5 и 8
- 13 — это 6 и 7
- 14 — это 4 и 10
- 14 — это 5 и 9
- 14 — это 6 и 8
- 14 — это 7 и 7
- 15 — это 5 и 10
- 15 — это 6 и 9
- 15 — это 7 и 8
- 16 — это 6 и 10
- 16 — это 7 и 9
- 16 — это 8 и 8
- 17 — это 7 и 10
- 17 — это 8 и 9
- 18 — это 8 и 10
- 18 — это 9 и 9
- 19 — это 9 и 10
Таблицы сложения
Таблица сложения нужна, чтобы научиться быстрому сложению чисел.
Существует несколько таблиц сложения чисел. Одна из первых таблиц такого рода — таблица сложения в пределах 10, но если ты хорошо знаешь состав чисел, тебе она не понадобится.
Как пользоваться такой таблицей?
Например, тебе нужно узнать, сколько будет 4 + 5.
Есть очень простая таблица сложения чисел с переходом через десяток. Вот она.
Пользоваться ею, конечно, очень легко.
Но наиболее полная таблица сложения чисел в от 1 до 20 представлена ниже.
Как ею пользоваться? Очень просто.
Например, тебе нужно к 7 + 6:
А это сводная таблица, которой можно прользоваться, пока не заучишь её наизусть.
А такими таблицами можно пользоваться при заучивании результатов сложения наизусть.
Письменное сложение в столбик
Сложение
Правило встречается в следующих упражнениях:
1 класс
- Страница 76, Моро, Волкова, Степанова, Учебник, 2 часть
- Страница 77, Моро, Волкова, Степанова, Учебник, 2 часть
- Страница 85, Моро, Волкова, Степанова, Учебник, 2 часть
- Страница 104, Моро, Волкова, Степанова, Учебник, 2 часть
- Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть
- Страница 38, Моро, Волкова, Рабочая тетрадь, 2 часть
- Страница 40, Моро, Волкова, Рабочая тетрадь, 2 часть
- Страница 44, Моро, Волкова, Рабочая тетрадь, 2 часть
- 2 класс
- Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Задание 2, Моро, Волкова, Рабочая тетрадь, 1 часть
- Задание 52, Моро, Волкова, Рабочая тетрадь, 1 часть
- Задание 132, Моро, Волкова, Рабочая тетрадь, 1 часть
- Задание 144, Моро, Волкова, Рабочая тетрадь, 1 часть
- Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
- Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
- Страница 48, Моро, Волкова, Рабочая тетрадь, 2 часть
- 3 класс
- Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Страница 31, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
- Страница 6, Моро, Волкова, Рабочая тетрадь, 1 часть
- Страница 11, Моро, Волкова, Рабочая тетрадь, 1 часть
- Страница 4, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
- Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
- Страница 7, Моро, Волкова, Рабочая тетрадь, 2 часть
- 5 класс
- Упражнение 166, Мерзляк, Полонский, Якир, Учебник
- budu5.com, 2020
- Пользовательское соглашение
- Copyright
- Нашли ошибку?
- Связаться с нами
Вычитание произвольных чисел
Рассмотрим правило, когда вычитаемое разлагается на цифры. После представления числа в виде суммы битов используется описанное выше свойство вычитания. Вычитание начинается с единиц, затем десятков, сотен и так далее.
Пример 22
Рассчитаем 45−32.
Разложим 32 на цифры: 32=30+2. У нас есть 45−32=45−(30+2). Представьте, как 45−(30+2)=45−(2+30). Теперь воспользуемся свойством вычитания суммы из числа: 45−(2+30) =(45−2)−30. Осталось вычислить 45−2, а затем вычесть число 30.
Изучив предыдущие правила, вы легко сможете это сделать.
Итак, 45−2=(40+5)−2=40+(5−2)=40+3=43. Тогда (45−2)−30=43−30. Осталось представить приведенное в виде суммы битовых слагаемых и завершить вычисления: 43−30=(40+3)−30=(40−30)+3=10+3=13
Все решение удобно записать в виде цепочки равенств:
45−32=45−(2+30)=(45−2)−30=((40+5)−2)−30==(40+(5−2))−30=(40+3) −30=(40−30)+3=10+3=13
Немного усложним пример.
Вычтите 18 из 85.
Разложим число 18 на цифры, и получим 18 = 10 + 8. Поменяем местами члены: 10+8=8+10. Теперь мы вычтем полученную сумму битовых терминов из числа 85 и воспользуемся свойством вычесть сумму из числа: 85−18=85−(8+10) =(85−8)−10. Вычисляем разницу в скобках:
85−8=(80+5)−8=(80−8)+5=((70+10)−8)+5=(70+(10−8))+5=(70+2)+ 5=70+7=77
Тогда (85−8)−10=77−10=(70+7)−10=(70−10)+7=60+7=67
Для закрепления материала разберем решение еще одного примера.
Пример 23
Вычтите из числа 23555 число 715.
Поскольку 715=700+10+5=5+10+700=5+(10+700), то 23555-715=23555-(5+10+700). Вычтите сумму из числа следующим образом: 23555−(5+(10+700))=(23555−5)−(10+700).
Вычислить разницу в скобках:
23 555−5=(20 000+3 000+500+50+5)−5=20 000+3 000+500+50+(5−5)==20 000+3 000+500+50+0= 20 000+50,00+=23 550.
Тогда (23555−5)−(10+700)=23550−(10+700).
Еще раз обратимся к свойству вычитания натурального числа из суммы: 23 550−(10+700)=(23 550−10)−700.
(23 550−10)−700=23 540−700=(20 000+3 000+500+40)−700==20 000+(3 000−700)+500+40
Отнимите 700 от 3000 и: 3000-700=(2000+1000)-700=2000+(1000-700)=2000+300=2300, тогда 20000+(3000-700)+500,+00=500,+00 = +40=22 840.
Вычитание произвольных натуральных чисел.
Осталось рассмотреть вычитание натуральных чисел, когда вычитаемое раскладывается в сумму разрядных слагаемых. В этом случае вычитание проводится следующим образом: после представления вычитаемого в виде суммы разрядных слагаемых используется необходимое количество раз. Причем сначала удобнее вычитать единицы, затем – десятки, далее – сотни и т.д.
Для примера вычислим разность 45−32. Раскладываем вычитаемое 32 по разрядам: 32=30+2. Имеем 45−32=45−(30+2). Для удобства в скобках переставим слагаемые местами 45−(30+2)=45−(2+30) (это мы можем делать в силу ). Теперь применяем свойство вычитания суммы из числа: 45−(2+30)=(45−2)−30. Осталось вычислить разность 45−2, после чего от полученного результата отнять число 30. Выполнение этих действий не вызовет затруднений, если Вы хорошо усвоили материал предыдущих пунктов. Итак, 45−2=(40+5)−2=40+(5−2)=40+3=43. Тогда (45−2)−30=43−30. Осталось представить уменьшаемое в виде суммы разрядных слагаемых и закончить вычисления: 43−30=(40+3)−30=(40−30)+3=10+3=13.
Все решение удобно записывать в виде цепочки равенств:45−32=45−(2+30)=(45−2)−30=((40+5)−2)−30=
=(40+(5−2))−30=(40+3)−30=(40−30)+3=10+3=13.
Немного усложним пример. Вычтем из числа 85 число 18. Раскладываем по разрядам число 18, при этом получаем 18=10+8. Меняем местами слагаемые: 10+8=8+10. Теперь вычитаем полученную сумму разрядных слагаемых из числа 85 и применяем свойство вычитания суммы из числа: 85−18=85−(8+10)=(85−8)−10.
Вычисляем разность в скобках:85−8=(80+5)−8=(80−8)+5=((70+10)−8)+5=(70+(10−8))+5=(70+2)+5=70+7=77.
Тогда (85−8)−10=77−10=(70+7)−10=(70−10)+7=60+7=67.
Для закрепления материала разберем решение еще одного примера.
Отнимем от числа 23 555 число 715. Так как 715=700+10+5=5+10+700=5+(10+700), то 23 555−715=23 555−(5+10+700). Вычитаем сумму из числа следующим образом: 23 555−(5+(10+700))=(23 555−5)−(10+700).
Вычислим разность в скобках:23 555−5=(20 000+3 000+500+50+5)−5=20 000+3 000+500+50+(5−5)=
=20 000+3 000+500+50+0=20 000+3 000+500+50=23 550.
Тогда (23 555−5)−(10+700)=23 550−(10+700). Еще раз обращаемся к свойству вычитания натурального числа из суммы: 23 550−(10+700)=(23 550−10)−700.
Опять вычисляем разность в скобках:23 550−10=(20 000+3 000+500+50)−10=20 000+3 000+500+(50−10)=
=20 000+3 000+500+40=23 540.
Имеем(23 550−10)−700=23 540−700=(20 000+3 000+500+40)−700=
=20 000+(3 000−700)+500+40.
Вычтем из 3 000 число 700 и этот результат подставим в последнюю сумму: 3 000−700=(2 000+1 000)−700=2 000+(1 000−700)=2 000+300=2 300, тогда 20 000+(3 000−700)+500+40=20 000+2 300+500+40=22 840.
В заключение этого пункта необходимо отметить, что для вычитания двух натуральных чисел удобно использовать специальный метод, который получил название вычитание столбиком.
Как быстро и легко выучить таблицу умножения с ребёнком?
Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.
Совет №1
Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.
Умножение – это сумма одинаковых слагаемых.
8 умножить на 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8
Понимая смысл умножения, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.
Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.
Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32
Умножать можно с помощью рук
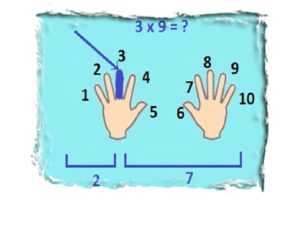
Умножение на 9
Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.
Вычисление произведения любых однозначных чисел больше, чем 5
Способ 1
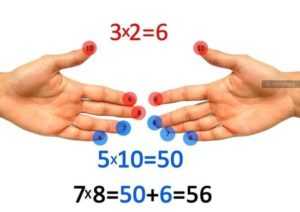
Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).
Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.
Способ 2
Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.
В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42
Проверьте и убедитесь, что эти способы действительно работают.
Совет № 3
Знание правил умножения упростит запоминание таблицы умножения:
- При умножении любого числа на 1 получается то число, которое умножали.
- Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
- Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
- Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
- При умножении на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.
Научиться пользоваться таблицей Пифагора
Необходимо показать ребёнку, что числа из левого столбика умножаются на числа из верхней строки. Найти результат очень просто: нужно только провести рукой по таблице вниз и вправо от множителей до места пересечения, где и будет расположен результат умножения.
Возьмите пустую распечатанную или нарисованную таблицу и заполните её вместе с ребёнком. Причем в цвете, закрашивая одинаковый результат одним цветом. Сразу будет видна закономерность. Ребёнок увидит, что запоминать нужно только половину таблицы (согласно переместительному закону умножения).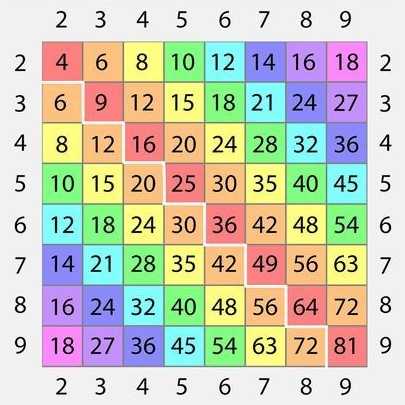
Понимая смысл умножения, можно использовать для вычислений предыдущие или последующие табличные случаи. При этом случае нужно лишь вычесть или прибавить нужное число.
Таблица умножения и игра, чтобы быстро выучить

С лучшей бесплатной игрой таблица умножения учится очень быстро. Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа.
Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять).
Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Таблица умножения – таблица, где строки и столбцы озаглавлены множителями (1, 2, 3, 4, 5…), а ячейки таблицы содержат их произведение. Применяется таблица для обучения умножению. Здесь есть игра и картинка для печати. Для скачивания игры с таблицей на компьютер, сохраните страницу (Ctrl+S). Также посмотрите таблицу деления.
Смотрите ниже шпаргалки в полной форме.
Распечатать таблицу умножения
Умножение прямо на сайте (онлайн)
https://uchim.org/matematika/tablica-umnozheniya — uchim.org
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Всё для учебы » Математика в школе » Таблица умножения и игра, чтобы быстро выучить
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е. Э.Кочурова
В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку.
Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.

Табличное сложение / Сложение / Справочник по математике для начальной школы
- Главная
Справочники
Справочник по математике для начальной школы
Сложение
Табличное сложение
Прежде чем познакомиться с таблицами сложения чисел, мы рассмотрим случаи сложения разных видов.
Например, 7 + 6 = ?
Мы видим, что сумма будет больше 10, потому что 10 – это 7 и 3. Мы будем прибавлять число 6 по частям.
Сначала прибавляем столько, чтобы получить 10: 7 + 3 = 10.
Дальше мы вспоминаем, что 6 — это 3 и 3.
Число 3 мы уже прибавили, значит, надо прибавить ещё 3: 10 + 3 = 13.
Тогда наш пример 7 + 6 можно записать по-другому:
или так:
Значит, 7 + 6 = 13
Рассуждая так, можно решить любой пример на сложение в пределах 20.
Случаи табличного сложения
11 – это 1 и 10
11 – это 2 и 9
11 – это 3 и 8
11 – это 4 и 7
11 – это 5 и 6
12 – это 2 и 10
12 – это 3 и 9
12 – это 4 и 8
12 – это 5 и 7
12 – это 6 и 6
13 – это 3 и 10
13 – это 4 и 9
13 – это 5 и 8
13 – это 6 и 7
14 – это 4 и 10
14 – это 5 и 9
14 – это 6 и 8
14 – это 7 и 7
15 – это 5 и 10
15 – это 6 и 9
15 – это 7 и 8
16 – это 6 и 10
16 – это 7 и 9
16 – это 8 и 8
17 – это 7 и 10
17 – это 8 и 9
18 – это 8 и 10
18 – это 9 и 9
19 – это 9 и 10
Таблицы сложения
Таблица сложения нужна, чтобы научиться быстрому сложению чисел.
Существует несколько таблиц сложения чисел. Одна из первых таблиц такого рода – таблица сложения в пределах 10, но если ты хорошо знаешь состав чисел, тебе она не понадобится.
Как пользоваться такой таблицей?
Например, тебе нужно узнать, сколько будет 4 + 5.
Есть очень простая таблица сложения чисел с переходом через десяток. Вот она.
Пользоваться ею, конечно, очень легко.
Но наиболее полная таблица сложения чисел в от 1 до 20 представлена ниже.
Как ею пользоваться? Очень просто.
Например, тебе нужно к 7 + 6:
А это сводная таблица, которой можно прользоваться, пока не заучишь её наизусть.
А такими таблицами можно пользоваться при заучивании результатов сложения наизусть.
Письменное сложение в столбик
Сложение
Правило встречается в следующих упражнениях:
1 класс
Волкова, Проверочные работы
Моро, Волкова, Степанова, Учебник, 2 часть
Моро, Волкова, Степанова, Учебник, 2 часть
Моро, Волкова, Степанова, Учебник, 2 часть
Моро, Волкова, Степанова, Учебник, 2 часть
Моро, Волкова, Степанова, Учебник, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
2 класс
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 74,
Моро, Волкова, Рабочая тетрадь, 1 часть
Задание 92,
Моро, Волкова, Рабочая тетрадь, 1 часть
Задание 133,
Моро, Волкова, Рабочая тетрадь, 1 часть
Моро, Волкова, Проверочные работы
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Моро, Волкова, Рабочая тетрадь, 1 часть
Моро, Волкова, Проверочные работы
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Моро, Волкова, Рабочая тетрадь, 2 часть
2019 – budu5.com, Буду отличником!
Вычитание чисел на координатном луче
Рассмотрим, что такое вычитание с геометрической точки зрения. Мы используем координатный луч. Вычитание числа b из a на координатном луче происходит следующим образом: определяем точку, координата a.Откладываем в сторону точки O единичных отрезков в количестве, определяемом вычитаемым b.Так находим точку на координатном луче координата равна разности a−b. Другими словами, это движение влево от точки с координатой a на расстояние b, чтобы попасть в точку с координатой a−b.
Оцените вычитание на координатном луче, используя рисунок. Итак, мы приходим в точку с координатой 2, так что 6−4=2.






























