Правила возведения в степень комплексного числа

Возведение комплексного числа в большую степень — декартова форма

спросил 4 года 3 месяца назад

Изменено
4 года, 3 месяца назад

Просмотрено
2к раз

$\begingroup$

Мой вопрос касается возведения комплексного числа в большую степень. Я знаю, как это сделать с помощью закона Муавра, но мне нужно получить результат в декартовой форме, например $z=x+iy$. и без тригонометрических членов. 99$.

$\endgroup$

$\begingroup$

Если вы воспользуетесь формулой Де Муавра и получите $r(\cos x + i\sin x)$, то просто распределите $r$, чтобы получить $$r\cos x + (r\sin x)i$$
Теперь просто оцените функцию косинуса и синуса, и у вас останется комплексное число в форме $a+bi$.

История[]

Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Дж. Кардано (1545), который счёл их непригодными к употреблению.
Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни выражаются через кубические корни из мнимых величин), впервые оценил
Р. Бомбелли (1572).
Он же дал некоторые простейшие правила действий с комплексными числами.
Выражения вида a+b−1{\displaystyle a+b{\sqrt {-1}}}, появляющиеся при решении квадратных и кубических уравнений, стали называть в XVI­­­­-XVII вв. «мнимыми».
Однако даже для многих крупных учёных XVII в. алгебраическая и геометрическая сущность мнимых величин представлялась неясной.
Известно, например, что Ньютон не включал мнимые величины в понятие числа, а Лейбницу принадлежит фраза: «Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием».

Зодача о выражении корней степени n{\displaystyle n} из данного числа была в основном решена в работах А. Муавра
(A. de Moivre, 1707, 1724) и Р. Котеса (R. Cotes, 1722).
Символ i=−1{\displaystyle i={\sqrt {-1}}} предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова imaginarius.
Он же высказал в 1751 мысль об алгебраической замкнутости поля комплексных чисел, к такому же выводу
пришел Д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит
Гауссу (1799). Он же ввёл в употребление термин «комплексное число» в 1831.
Полное геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе К. Весселя (С. Wessel, 1799).
Геометрическое представление комплексных чисел, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806 и 1814 работы Ж. Р. Аргана (J. R. Argand), повторявшей независимо выводы К. Весселя.

Арифметическая теория комплексных чисел как пар вещественных чисел была построена У. Р. Гамильтоном (1837).
Ему же принадлежит обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.

Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

\

Возведём его в квадрат, умножив на само себя:

\

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

\

в степень $n\in \mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $n\in \mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

\

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

Тригонометрическая форма

\

где $\left| z \right|$ — модуль комплексного числа, $\text\!\!\varphi\!\!\text$ — некоторый угол, который называется аргумент комплексного числа (пишут $\text\!\!\varphi\!\!\text=\arg \left( z \right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Переписываем исходное число в виде $z=\sqrt+1\cdot i$ и считаем модуль:

Выносим модуль за скобки:

\

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $\frac\!\!\pi\!\!\text>$ с тем же успехом можно взять аргумент $\frac\!\!\pi\!\!\text>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Как возвести комплексное число в степень: формула Муавра

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Возведение комплексного числа в натуральную степень

В данной публикации мы рассмотрим, как комплексное число можно возвести в степень (в т.ч. с помощью формулы Муавра). Теоретический материал сопровождается примерами для лучшего понимания.

• Возводим комплексное число в степень
  • Квадрат числа
  • N-ая степень

Для начала вспомним, что комплексное число имеет общий вид: z = a + bi (алгебраическая форма).

Теперь можем переходить, непосредственно, к решению поставленной задачи.

Квадрат числа

Мы можем представить степень в виде произведения одинаковых множителей, а затем найти их произведение (при этом помним, что i2 = -1).

z2 = (a + bi)2 = (a + bi)(a + bi)

Пример 1:z = 3 + 5iz2 = (3 + 5i)2 = (3 + 5i)(3 + 5i) = 9 + 15i + 15i + 25i2 = -16 + 30i

Также можно воспользоваться формулой сокращенного умножения, а именно квадратом суммы:

z2 = (a + bi)2 = a2 + 2 ⋅ a ⋅ bi + (bi)2 = a2 + 2abi – b2

Примечание: Таким же образом, если потребуется, можно получить формулы для квадрата разности, куба суммы/разности и т.д.

N-ая степень

Возвести комплексное число z в натуральную степень n гораздо проще, если оно представлено в тригонометрической форме.

Напомним, в общем виде запись числа выглядит так: z = |z| ⋅ (cos φ + i ⋅ sin φ).

Для возведения в степень можно воспользоваться формулой Муавра (так названа в честь английского математика Абрахама де Муавра):

zn = |z|n ⋅ (cos (nφ) + i ⋅ sin (nφ))

Формула получена путем перемножения комплексных чисел, записанных в тригонометрической форме (перемножаются модули, а аргументы складываются).

Пример 2 Возведем комплексное число z = 2 ⋅ (cos 35° + i ⋅ sin 35°) в восьмую степень.

Решениеz8 = 28 ⋅ (cos (8 ⋅ 35°) + i ⋅ sin (8 ⋅ 35°)) = 256 ⋅ (cos 280° + i sin 280°).

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.

ГЛАВНАЯ » Материалы для обучения

Умножение комплексных чисел

Деление комплексных чисел

Формула Муавра

Задание комплексных чисел в тригонометрической форме удобно при выполнении над числами действий умножения, деления, возведения в степень и извлечения корня.
Найдем произведение двух комплексных чисел, записанных в тригонометрической форме; пусть
$z_{1} = r_{1} (\cos \phi_{1} + i \sin \phi_{1}), z_{2} = r_{2} (\cos \phi_{2} + i \sin \phi_{2}).$
Получаем
$z_{1}z_{2} = r_{1}r_{2} $.
Выражения, стоящие в круглых скобках, можно упростить:
$\cos \phi_{1} \cos \phi_{2} — \sin \phi_{1} \sin \phi_{2} = \cos (\phi_{1} + \phi_{2})$,
$\sin \phi_{1} \cos \phi_{2} + \sin \phi_{2} \cos \phi_{1} = \sin (\phi_{1} + \phi_{2})$.
Таким образом,
$z_{2}z_{1} = r_{1} r_{2} $. (1)
Доказано правило: для умножения чисел, заданных в тригонометрической форме, их модули надо перемножить, а аргументы сложить.это правило остается верным для любого количества сомножителей.
Пример 1. Найти произведение чисел
$z_{1} = \sqrt{2} (\cos 28^{\circ} + i \sin 25^{\circ}), z_{2} = \sqrt{4} (\cos 35^{\circ} + i \sin 35^{\circ})$
Решение.
$z_{1}z_{2} = sqrt{2} \sqrt{4} = 2 (\cos 60^{\circ} + i \sin 60^{\circ}) = 1 + i \sqrt{3}$
Так как деление — действие, обратное умножению, то легко вывести следующее правило:
для выполнения деления двух комплексных чисел, заданных в тригонометрической форме, следует их модули разделить, а аргументы вычесть:
$\frac{z_{1}}{z_{2}} = \frac{r_{1}}{r_{2}} $. (2)Пример 2. Найти частное от деления числа $z_{1} = 6 (\cos 110^{\circ} + i \sin 110^{\circ})$ на число $z_{2} = 2 (\cos 80^{\circ} + i \sin 80^{\circ})$.
Решение. Находим по формуле (2):
$\frac{z_{1}}{z_{2}} = \frac{6}{2} (\cos 30^{\circ} + i \sin 30^{\circ}) = \frac{3 \sqrt{3}}{2} + \frac{3}{2} i$
Используем теперь равенство (1) для возведения произвольного комплексного числа $z = r (\cos \phi + i \sin \phi)$ в натуральную степень $n$. Для этого придется модуль $r$ этого числа взять множителем $n$ раз и аргумент $\phi$ взять слагаемым $n$ раз. Это приводит к равенству
$z^{n} = r^{n} (\cos n \phi + i \sin n \phi)$ (3)
Равенство (3) называется формулой Муавра. Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель степени.
Пример 3. Вычислить $^{5}$.
Решение. В соответствии с формулой Муавра (3)
$^{5} = 243 (\cos 215^{\circ} + i \sin 215^{\circ})$
Если число $z$ задано в алгебраической форме $a+bi$, то для возведения его в степень с помощью формулы Муавра надо предварительно записать его в тригонометрической форме.

Проверка

Доказано, что это верно для n = k + 1.

Поскольку zк + 1= zk _* z, то zк + 1 = (r (cos Ɵ + i _* сен Ɵ))к + 1 = гk (cos kƟ + i _* сен кƟ) _*  г (соз Ɵ + я_* сенƟ).

Затем выражения умножаются:

zк + 1 = гк + 1((cos kƟ)_*(cosƟ) + (cos kƟ)_*(я_*senƟ) + (я _* сен кƟ)_*(cosƟ) + (я _* сен кƟ)_*(я_* сенƟ)).

На мгновение фактор r игнорируетсяк + 1, а общий множитель i берется:

(cos kƟ)_*(cosƟ) + i (cos kƟ)_*(sinƟ) + я (грех kƟ)_*(cosƟ) + я2(сен кƟ)_*(сенƟ).

Как и я2 = -1, подставляем в выражение и получаем:

(cos kƟ)_*(cosƟ) + i (cos kƟ)_*(sinƟ) + я (грех kƟ)_*(cosƟ) — (грех kƟ)_*(сенƟ).

Теперь заказаны действительная и мнимая части:

(cos kƟ)_*(cosƟ) — (грех kƟ)_*(sinƟ) + я [(sin kƟ)_*(cosƟ) + (cos kƟ)_*(сенƟ)].

Чтобы упростить выражение, для косинуса и синуса применяются тригонометрические тождества суммы углов:

соз (А + В) = соз А _* cos B — грех A _* сен Б.

грех (А + В) = грех А _* cos B — cos A _* cos B.

В данном случае переменными являются углы Ɵ и kƟ. Применяя тригонометрические тождества, мы имеем:

cos kƟ _* cosƟ — сэн ко _* sinƟ = cos (kƟ + Ɵ)

сен ко _* cosƟ + cos kƟ _* грех = грех (кƟ + Ɵ)

Таким образом, выражение выглядит так:

zк + 1 = гк + 1 (cos (kƟ + Ɵ) + я _* грех (kƟ + Ɵ))

zк + 1 = гк + 1(cos + я _* грех ).

Таким образом, можно показать, что результат верен для n = k + 1. По принципу математической индукции делается вывод, что результат верен для всех положительных целых чисел; то есть n ≥ 1.

Возводим комплексное число в степень

Для начала вспомним, что комплексное число имеет общий вид: (алгебраическая форма).

Теперь можем переходить, непосредственно, к решению поставленной задачи.

Квадрат числа

Мы можем представить степень в виде произведения одинаковых множителей, а затем найти их произведение (при этом помним, что ).

Пример 1: z = 3 + 5i z 2 = = = =

Также можно воспользоваться формулой сокращенного умножения, а именно квадратом суммы:

Примечание: Таким же образом, если потребуется, можно получить формулы для квадрата разности, куба суммы/разности и т.д.

N-ая степень

Возвести комплексное число z в натуральную степень n гораздо проще, если оно представлено в тригонометрической форме.

Напомним, в общем виде запись числа выглядит так: .

Для возведения в степень можно воспользоваться формулой Муавра (так названа в честь английского математика Абрахама де Муавра):

Формула получена путем перемножения комплексных чисел, записанных в тригонометрической форме (перемножаются модули, а аргументы складываются).

Пример 2 Возведем комплексное число в восьмую степень.

Возводим комплексное число в степень

Во-первых, помните, что комплексное число имеет общую форму: z = a + bi (алгебраическая форма).

Теперь можно перейти непосредственно к решению задачи.

Квадрат числа

Мы можем представить степень как произведение тех же множителей, а затем найти их произведение (помня при этом, что i2 = -1).

z2 = (а + bi)2 = (a + bi)(a + bi)

Пример 1:
г = 3 + 5i
z2 = (3 + 5i)2 = (3 + 5i)(3 + 5i) = 9 + 15i + 15i + 25i2 = -16 + 30i

Также можно использовать формулу сокращенного умножения, а именно квадрат суммы:

z2 = (a + bi)2 = a2 + 2 ⋅ a ⋅ bi + (bi)2 = a2 + 2abi – b2

Примечание: Аналогично при необходимости можно получить формулы квадрата разности, куба суммы/разности и т.д.

N-ая степень

Возведение комплексного числа z в натуральную степень n значительно проще, если оно представлено в тригонометрической форме.

Помните, что запись числа обычно выглядит так: z = |z| ⋅ (cos φ + i ⋅ sin φ).

Для возведения в степень можно использовать формулу Де Муавра (названную в честь английского математика Абрахама де Муавра):

zn = |z|n ⋅ (cos (nφ) + i ⋅ sin (nφ))

Формула получается умножением комплексных чисел, записанных в тригонометрической форме (перемножаются модули и складываются аргументы).

Пример 2
Возведем комплексное число z = 2 ⋅ (cos 35° + i ⋅ sin 35°) в восьмую степень.

Решение
z8 = 28 ⋅ (cos (8 ⋅ 35°) + i ⋅ sin (8 ⋅ 35°)) = 256 ⋅ (cos 280° + i sin 280°).

Примеры решения задач

Задача 1

Задача

Необходимо найти частное пары комплексных чисел:

(z_1 = 3+i) и (z_2 = 2-3i)

Решение:

Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.

(frac{z_1}{z_2} = frac{3+i}{2-3i} =)

Сопряженное комплексное число к знаменателю:

(overline{z_2} = 2+3i)

Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:

(= frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =)

Далее следует привести подобные слагаемые и записать вывод с ответом:

(= frac{3 + 11i}{13} = frac{3}{13} + frac{11}{13}i)

Ответ: (frac{z_1}{z_2} = frac{3}{13} + frac{11}{13}i)

Задача 2

Задача

Требуется выполнить деление комплексных чисел:

(z_1 = 2(cos frac{pi}{3} + isin frac{pi}{6}))

(z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6}))

Решение:

Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:

Деление модулей:

(frac{r_1}{r_2} = frac{2}{4} = frac{1}{2})

Разность аргументов:

(varphi_1 — varphi_2 = frac{pi}{3} — frac{pi}{6} = frac{pi}{6})

Следующим шагом является деление чисел:

(frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Ответ: (frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Задача 3

Задача

Нужно найти частное комплексных чисел:

(z_1 = 3e^{frac{pi}{2}i})

(z_2 = 4e^{frac{pi}{4}i})

Решение:  Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:

(frac{r_1}{r_2} = frac{3}{4})

(varphi_1 — varphi_2 = frac{pi}{2} — frac{pi}{4} = frac{pi}{4})

При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:

(frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Ответ: (frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Задача 4

Задача

Определить частное:

(frac{-2+i}{1-i})

Решение:

В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:

(1-i)

Данным числом является:

(1+i)

Таким образом:

(frac{-2+i}{1-i}=frac{-2+i}{1-i} cdot frac{1+i}{1+i}=frac{(-2+i)(1+i)}{(1-i)(1+i)})

Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:

(i^{2}=-1)

(frac{-2+i}{1-i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}=frac{-2-2 i+i-1}{1^{2}-i^{2}}=)

(=frac{-3-i}{1-(-1)}=frac{-3-i}{2}=-frac{3}{2}-frac{i}{2})

Ответ:( frac{-2+i}{1-i}=-frac{3}{2}-frac{i}{2})

Задача 5

Задача

Необходимо найти частное:

(frac{z_{1}}{z_{2}})

При условии, что:

(z_{1}=2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right))

(z_{2}=cos frac{pi}{4}+i sin frac{pi}{4})

Решение:

Искомое частное:

(frac{z_{1}}{z_{2}}=frac{2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)}{cos frac{pi}{4}+i sin frac{pi}{4}}=)

(=frac{2}{1} cdotleft=)

(=2 cdotleft=2 cdot(0+i)=2 i)

Ответ: (frac{z_{1}}{z_{2}}=2 cdotleft(cos frac{pi}{2}+i sin frac{pi}{2}right)=2 i)

Задача 6

Задача

Необходимо разделить два комплексных числа:

(z_{1}=-1+3i)

(z_{2}=1+2i)

Решение:

С помощью соответствующей формулы можно записать уравнение:

(z_{1} div z_{2} = frac{-1+3i}{1+2i} = frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = frac{-1 cdot 1 + 3 cdot 2}{1^{2}+2^{2}} + i frac{3 cdot 1 + (-1) cdot (-2)}{1^{2}+2^{2}} =)

(= frac{5}{5} + i frac{5}{5}=1+i)

Ответ: ( z_{1} div z_{2} = 1+i)

Задача 7

Задача

Необходимо вычислить частное комплексных чисел:

(z_{1}=sqrt{2} left( cos frac{pi}{2} + i sin frac{pi}{2} right))

(z_{2}=sqrt{2} left( cos frac{pi}{4} + i sin frac{pi}{4} right))

Решение:

Используя соответствующую формулу, запишем:

(z_{1} div z_{2} = frac{r_{1}}{r_{2}} (cos ( varphi _{1} — varphi _{2}) + i sin ( varphi _{1} — varphi _{2})) = frac{sqrt{2}}{sqrt{2}} left( cos left( frac{pi}{2}-frac{pi}{4} right) + i sin left( frac{pi}{2}-frac{pi}{4} right) right) =)

(= 1 cdot left( cos frac{pi}{4} + i sin frac{pi}{4} right) = cos frac{pi}{4} + i sin frac{pi}{4})

Ответ:( z_{1} div z_{2} = cos frac{pi}{4} + i sin frac{pi}{4})

Задача 8

Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

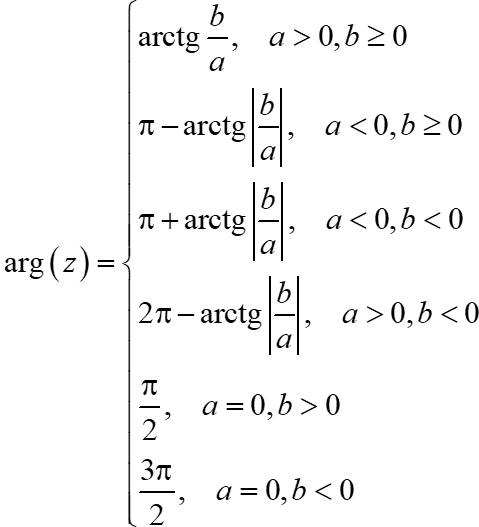
Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

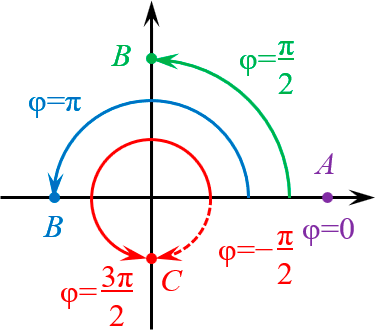
• На положительной полуоси абсцисс $\varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $\varphi =\pi $ (синяя точка $B$).
• На положительной полуоси ординат $\varphi =\frac$ (зелёная точка $B$).
• На отрицательной — $\varphi =\frac$ (красная точка $C$). Однако ничто не мешает рассмотреть $\varphi =-\frac$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $a\ne 0$ и $b\ne 0$. Рассмотрим вспомогательный угол

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $_>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

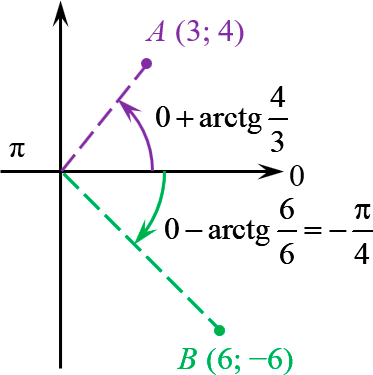
Точка $A\left( 3;4 \right)$ удалена от начала координат на расстояние 5:

\

Для точки $B\left( 6;-6 \right)$ арктангенс оказался табличным:

\

В левой полуплоскости откладываем от луча, соответствующего углу $\pi $:

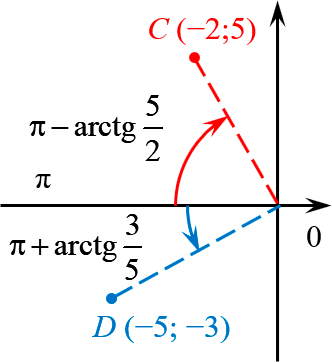
Итого для точки $C\left( -2;5 \right)$ имеем:

\

И, наконец, для точки $D\left( -5;-3 \right)$:

\

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Другие действия над комплексными числами

Помимо основных операций сложения, вычитания, умножения и деления комплексных чисел, существуют также различные математические функции. Рассмотрим некоторые из них:

• Получить действительную часть числа: Re(z) = a
• Получить мнимую часть числа: Im(z) = b
• Числовой модуль: |z| = √(a2 + b2)
• Числовой аргумент: arg z = arctg(b / a)
• Показатель степени: ez = ea cos(b) + i ea sin(b)
• Логарифм: Ln(z) = ln |z| + в аргументе (z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arc z, arth z, arcth z

Отрицательное целое число

Теорема Муавра также применяется, когда n ≤ 0. Рассмотрим отрицательное целое число «n»; тогда «n» можно записать как «-m», то есть n = -m, где «m» — положительное целое число. Таким образом:

(cos Ɵ + i _* сен Ɵ) п = (cos Ɵ + i _* сен Ɵ) -м

Чтобы получить показатель степени «m» положительным образом, выражение записывается в обратном порядке:

(cos Ɵ + i _* сен Ɵ) п = 1 ÷ (cos Ɵ + i _* сен Ɵ) м

(cos Ɵ + i _* сен Ɵ) п = 1 ÷ (cos mƟ + i _* сен мƟ)

Теперь используется, что если z = a + b * i — комплексное число, то 1 ÷ z = a-b * i. Таким образом:

(cos Ɵ + i _* сен Ɵ) п = cos (mƟ) — я _* сен (мƟ).

Используя cos (x) = cos (-x) и -sen (x) = sin (-x), мы имеем:

(cos Ɵ + i _* сен Ɵ) п = [cos (mƟ) — я _* сен (мƟ)]

(cos Ɵ + i _* сен Ɵ) п = cos (- mƟ) + я _* сен (-mƟ)

(cos Ɵ + i _* сен Ɵ) п = cos (nƟ) — я _* сен (n).

Таким образом, можно сказать, что теорема применима ко всем целым значениям «n».