Объем конуса, его расчет

Элементы конуса

Определение. Вершиной конуса является точка (К), из которой выходят лучи. Определение. Основание конуса — это плоскость, образованная пересечением плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основания, как окружность, эллипс, гипербола и парабола. Определение Образующая конуса (L) — это любой отрезок, соединяющий вершину конуса с границей основания конуса. Образующая — это отрезок луча, выходящего из вершины конуса):

Л 2 = Р 2 + Н 2

Определение. Направляющая конуса – это кривая, описывающая контур основания конуса. Определение. Боковая поверхность конуса есть сумма всех образующих конуса. То есть поверхность, образованная движением образующей по направляющей конуса Определение Поверхность конуса состоит из боковой поверхности и основания конуса Определение Высота конуса (Н) – это отрезок, выходящий из вершине конуса и перпендикулярна основанию. Определение. Ось конуса (а) представляет собой прямую линию, проходящую через вершину конуса и центр основания конуса. Определение конусности (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса это отношение разности диаметров сечений D и d усеченного конуса и расстояния между ними:

С =	Д	и С =	Д — д
ЧАС	час

где C — конусность, D — диаметр основания, d — диаметр меньшего основания, h — расстояние между основаниями.
Конусность характеризует остроту конуса, то есть угол наклона образующей к основанию конуса. Чем больше конусность, тем острее будет угол наклона угла конусности α:

α = 2 угл	Р
ЧАС

где R — радиус основания, H — высота конуса.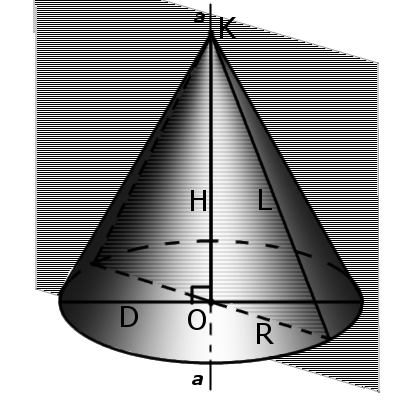
Определение: осевым сечением конуса называется сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, где стороны образованы образующими, а основание треугольника является диаметром основания конуса.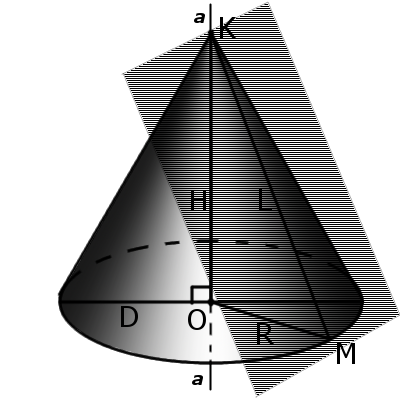
Определение: Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению конуса. Конус, покоящийся на окружности, эллипсе, гиперболе или параболе, называется круговым, эллиптическим, гиперболическим или параболическим конусом соответственно (последние два имеют бесконечный объем).
Определение: Прямой конус — это конус, ось которого перпендикулярна основанию. У такого конуса ось совпадает с высотой, а все образующие равны между собой Формула Объем круглого конуса:

В =	1	πHR2
3

где R — радиус основания, а H — высота конуса. Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:

Sb=πRL

Формула. Суммарная площадь поверхности (Sp) прямого кругового конуса по радиусу R и длине образующей L:

Sp = πRL + πR2

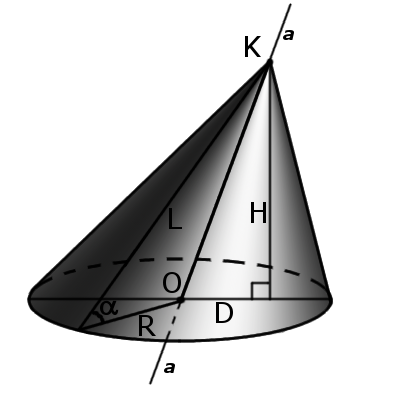
Определение: Наклонный (наклонный) конус – это конус, ось которого не перпендикулярна основанию. У такого конуса ось не совпадает с высотой Формула Объем любого конуса:

В =	1	Ш
3

где S — площадь основания, а H — высота конуса.
Определение. Усеченный конус — это часть конуса, расположенная между основанием конуса и плоскостью сечения, параллельной основанию. Формула. Объем усеченного конуса:

В =	1	(S2H-S1h)
3

где S1 и S2 — площади меньшего и большего основания соответственно, а H и h — расстояние от вершины конуса до центра нижнего и верхнего основания соответственно.

Почему пожарные ведра имеют форму конуса?

Кто задумывался, почему пожарные ведра имеют, казалось бы, странную коническую форму? А это не просто так. Оказывается, коническое ведро при тушении пожара имеет много преимуществ перед обычным, имеющим форму усеченного конуса.

Во-первых, как оказывается, пожарное ведро быстрее наполняется водой и при переноске она не расплескивается. Конус, объем которого больше обычного ведра, за один раз позволяет перенести больше воды.

Во-вторых, воду из него можно выплеснуть на большее расстояние, чем из обычного ведра.

В-третьих, если коническое ведро сорвется с рук и упадет в огонь, то вся вода выливается на очаг возгорания.

Все перечисленные факторы позволяют сэкономить время — главный фактор при тушении пожара.

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

• из круглого прямого конуса;
• с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной

Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр

Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

Разрезать ее вдоль образующей и развернуть на плоскости

Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор. Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G

Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2. Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r12 + r22 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

Пример решения задачи

Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см 2 . При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.

Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:

S = S1 + S2 = pi*r1 2 + pi*r2 2 = 4*pi*r2 2 + pi*r2 2 = 5*pi*r2 2 .

Откуда получается:

r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.

Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.

Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:

g = ((r1-r2)^2 + h 2 )^0,5 = (2,52 2 + 15 2 )^0,5 = 15,21 см.

Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:

Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см 2 .

Построение развертки конуса на бумаге

Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.

В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.

Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:

Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.

Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.

В чем преимущество усеченного конуса как геометрической фигуры?

Усеченный конус — это геометрическая фигура, у которой основаниями являются две круглые плоскости, соединенные боковой поверхностью, которая имеет форму конуса, но сечение вдоль его высоты меньше его оснований.

Преимущества этой геометрической фигуры могут включать:

1. Усеченный конус имеет большую устойчивость, чем обычный конус, так как он имеет большую поверхность опоры на основаниях, что делает его лучшим выбором для некоторых приложений, например, при проектировании оболочек реакторов.
2. Усеченный конус может быть более экономичным в использовании материала, чем обычный конус, так как он имеет меньшую высоту, но сохраняет ту же площадь оснований. Это может быть полезно в проектировании строительных элементов, таких как колонны или башни.
3. Усеченный конус может иметь большую универсальность в применении, так как его форма может быть изменена путем изменения размеров его оснований и высоты. Это позволяет использовать усеченные конусы в различных областях, например, в качестве башенной опоры или формы для литья металла.
4. Усеченный конус может иметь более эргономичную форму, что делает его удобным в использовании в некоторых приложениях, например, при проектировании мебели или автомобильных деталей.
5. Усеченный конус может иметь более интересный внешний вид, что делает его привлекательным для использования в художественном дизайне или архитектуре.

В целом, усеченный конус является полезной геометрической фигурой, которая имеет множество преимуществ в различных областях применения.

Задача 5

Рис. 8. Вра­ща­е­мый тре­уголь­ник

Рис. 9. Тело, по­лу­чен­ное при вра­ще­нии рав­но­бед­рен­но­го тре­уголь­ни­ка

Рав­но­бед­рен­ный тре­уголь­ник, бо­ко­вая сто­ро­на ко­то­ро­го равна , а угол при ос­но­ва­нии равен , вра­ща­ет­ся во­круг сво­е­го ос­но­ва­ния (см. рис. 8). Найти пло­щадь по­верх­но­сти по­лу­чен­но­го при вра­ще­нии тела (см. рис. 9).

Ре­ше­ние

Рис. 10. Два рав­ных ко­ну­са

Если про­ве­сти в тре­уголь­ни­ке вы­со­ту из вер­ши­ны, то по­лу­ча­ет­ся два пря­мо­уголь­ных тре­уголь­ни­ка, вра­щая ко­то­рые мы по­лу­ча­ем два рав­ных ко­ну­са, при­ле­га­ю­щих друг к другу ос­но­ва­ни­я­ми (см. рис. 10).

Зна­чит, пло­щадь по­верх­но­сти ис­ко­мо­го тела равна удво­ен­ной пло­ща­ди бо­ко­вой по­верх­но­сти лю­бо­го из ко­ну­сов. Таким об­ра­зом, нам надо найти ра­ди­ус ос­но­ва­ния и об­ра­зу­ю­щую ко­ну­са (см. рис. 11).

Рис. 11. Ил­лю­стра­ция к по­след­не­му шагу

Ра­ди­ус ос­но­ва­ния ко­ну­са равен вы­со­те ис­ход­но­го тре­уголь­ни­ка, а об­ра­зу­ю­щая – бо­ко­вой сто­роне. Оче­вид­но, вы­со­та равна , а зна­чит, , таким об­ра­зом, окон­ча­тель­ный ответ: .

Ответ: .

Конус с круглым основанием

Прежде чем переходить к рассмотрению боковой поверхности конуса, покажем, что это за фигура и как ее получить геометрическими методами.

Возьмем прямоугольный треугольник ABC, у которого AB и AC являются катетами. Поставим этот треугольник на катет AC и будем его вращать вокруг катета AB. В результате стороны AC и BC опишут две поверхности фигуры, которая показана ниже.

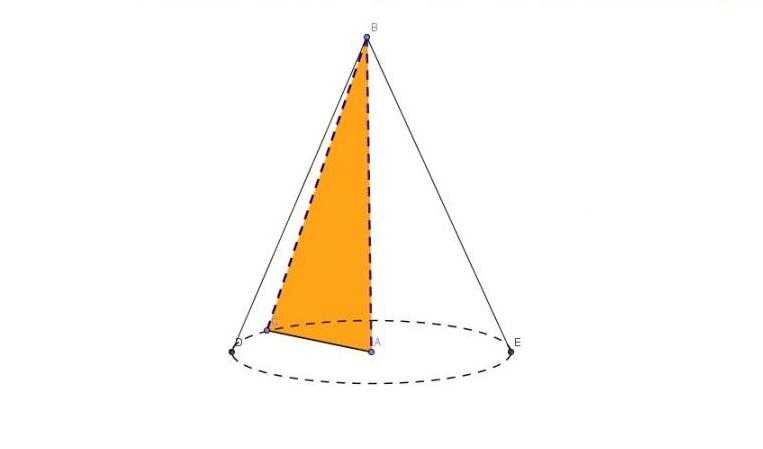
Полученная вращением фигура называется круглым прямым конусом. Круглый он потому, что его основание является кругом, а прямой потому, что проведенный из вершины фигуры (точка B) перпендикуляр пересекает круг в его центре. Длина этого перпендикуляра называется высотой. Очевидно, что она равна катету AB. Высоту принято обозначать буквой h.

Помимо высоты, рассматриваемый конус описывается еще двумя линейными характеристиками:

• образующая, или генератриса (гипотенуза BC);
• радиус основания (катет AC).

Радиус обозначим буквой r, а генератрису — g

Тогда, принимая во внимание теорему Пифагора, можно записать важное для рассматриваемой фигуры равенство:. g2 = h2 + r2

g2 = h2 + r2

Тест с ответами: “Цилиндр”

1. Дан цилиндр, длина диаметра основания которого в два раза меньше длины образующей. Объем этого цилиндра равен 108п. Вычислите диаметр основания: а) 6 + б) 14 в) 12

2. Что представляет сечение цилиндра, проведенное плоскостью, перпендикулярно оси: а) овал б) круг + в) прямоугольник

3. Вычислите длину радиуса основания равностороннего цилиндра, площадь полной поверхности которого равна 24п: а) 48 б) 12 в) 2 +

4. Что представляет осевое сечение цилиндра: а) прямоугольник + б) треугольник в) овал

5. Объем цилиндра равен произведению площади … на высоту: а) стороны б) вершины в) основания +

6. Что представляет боковая поверхность цилиндра: а) треугольник б) прямоугольник + в) круг

7. Сечение, проходящее параллельно основаниям цилиндра, является: а) прямоугольником б) квадратом в) кругом +

8. Объем цилиндра равен 64π, а площадь боковой поверхности – 32π. Найдите площадь полной поверхности цилиндра, деленную на π: а) 64 + б) 72 в) 48

9. Цилиндр, осевым сечением которого является квадрат, называется: а) правильным круглым б) эллиптическим в) равносторонним +

10. Про прямые круговые цилиндры C1 и C2 известно, что у C1 радиус основания в два раза больше, чем у C2, но у C2 высота в три раза больше, чем у C1. Найдите отношение объёма цилиндра C2 к объёму C1: а) 1 б) 0,75 + в) 1,2

11. Если диаметр основания и образующая цилиндра равны друг другу, то осевым сечением является: а) квадрат + б) круг в) прямоугольник

12. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали: а) 24 л б) 14 л + в) 12 л

13. Геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её: а) цилиндр + б) конус в) квадрат

14. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра: а) 1,20 б) 1,5 в) 1,25 +

15. Сечение, проходящее параллельно оси цилиндра, может быть: а) либо прямоугольником, либо квадратом + б) только квадратом в) только прямоугольником

16. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого: а) 18 см б) 3 см + в) 9 см

17. Если диаметр основания и образующая цилиндра не равны друг другу, то осевым сечением является: а) квадрат б) круг в) прямоугольник +

18. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали: а) 1100 см3 б) 1000 см3 + в) 100 см3

19. Вычислите длину высоты равностороннего цилиндра, площадь осевого сечения которого равна 25: а) 50 б) 12,5 в) 5 +

20. Пусть V, r, h соответственно объем, радиус и высота цилиндра. Найдите объем, если r=2√2 cм, h=3 см: а) 43π см3 б) 24π см3 + в) 31π см3

21. Сколько образующих можно провести в цилиндре: а) много + б) одну в) две

22. Радиус основания цилиндра равен 7, а высота – 10. Найдите площадь боковой поверхности цилиндра, деленную на π: а) 124 б) 140 + в) 104

23. Какой вид не может иметь сечение цилиндра: а) овал б) квадрат в) треугольник +

24. Шар вписан в цилиндр. Площадь поверхности шара равна 41. Найдите площадь полной поверхности цилиндра: а) 60 б) 61,5 + в) 55

25. Вращением какой геометрической фигуры можно получить цилиндр: а) прямоугольного треугольника вокруг гипотенузы б) прямоугольного треугольника вокруг катета в) прямоугольника вокруг одной из сторон +

26. Площадь боковой поверхности цилиндра равна 18π, а диаметр основания равен 9. Найдите высоту цилиндра: а) 4 б) 2 + в) 36

27. Площадь полной поверхности цилиндра: а) S=2п(r+h) + б) S= r(r+h) в) S=пr(r+h)

28. Поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей): а) поверхность основания цилиндра б) коническая поверхность в) цилиндрическая поверхность +

29. Площадь боковой поверхности цилиндра: а) S=пrh + б) S=2r в) S=r2

30. Отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка: а) сторона цилиндра б) высота цилиндра + в) вершина цилиндра

Объём конуса. Калькулятор объёма конуса онлайн

Объем конуса равен одной трети произведения площади основания на высоту

— тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называют также конусом вращения.

Связанные определения для конуса

Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.

Коническая поверхность. Образующая поверхность конуса является конической поверхностью.

Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.

Угол раствора конуса. Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).

Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.

Косой (наклонный) конус. Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.

Круговой конус. Круговой конус — конус, основание которого является кругом.

Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).

Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).

Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.

Объем прямого углового конуса

Конус — это геометрическое тело, которое образовано вращением прямоугольного треугольника около одного из его катетов.

Первый способ вычисления объема конуса

Объем конуса равен одной трети произведения площади основания на высоту

\

где:V — объем конусаS — площадь основания конусаH — высота конуса

Второй способ вычисления объема конуса

Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.

\

где:V — объем конусаH — высота конусаπ — число пи (3.1415)r — радиус конуса

Входные данные

Радиус r:

Высота h:

Количество знаков после запятой в результате вычислений

1234567

Результат

Объем усеченного конуса

Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.

Первый способ вычисления объема усеченного конуса

Объем усеченного конуса вычисляется по формуле:

\

где:V — объем конусаh — расстояния от плоскости верхнего основания до вершиныH — расстояния от плоскости нижнего основания до вершиныS₁ — площадь верхнего (ближнего к вершине) основанияS₂ — площадь нижнего основания

Второй способ вычисления объема усеченного конуса

Объем усеченного конуса вычисляется по формуле:

\

где:V — объем конусаh — высота конусаR — радиус нижнего основанияr — радиус верхнего основания

Калькулятор объема усечённого конуса

Входные данные

Радиус нижнего основания усечённого конуса R:

Радиус верхнего основания усечённого конуса r:

Высота усечённого конуса h:

Количество знаков после запятой в результате вычислений

1234567

Результат

В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Фигура конус

Прежде чем отвечать на вопрос о том, что это — усеченный конус, необходимо познакомиться с фигурой, от которой он образован. Конусом в геометрии принято называть фигуру, получаемую с помощью соединения прямыми отрезками некоторой точки пространства со всеми точками заданной кривой. Точка пространства не должна лежать в плоскости кривой, она называется вершиной конуса. Соединяющие отрезки — это образующие фигуры, а плоская кривая — это направляющая. Она ограничивает основание конуса. В свою очередь, совокупность всех образующих называется конической поверхностью. Конус, основанием которого является круг, показан на рисунке.

Расстояние между вершиной фигуры и основанием называется высотой. Если соответствующий перпендикуляр пересекает основание в геометрическом центре, то фигуру называют прямой.

Дальше в статье покажем, как, используя прямой круглый конус, получить усеченную фигуру.