Условие перевода обыкновенной дроби в десятичную
Давайте проверим и попробуем превратить в десятичную дробь $2\frac{3}{20}$
Разложим $20$ на простые множители. У нас получается $2, 5, 2$. Значит, эту дробь можно превратить в десятичную.
Для нахождения дополнительного множителя разделим $100$ на $20$, получится $5$.
Целые части дроби записываем без изменений, а числитель и знаменатель дробной части умножаем на дополнительные множители.
$$2\frac{3}{20} = 2\frac{3 \cdot 5}{20 \cdot 5} = 2\frac{15}{100} = 2.15$$
Попробуем другой пример.
$$5\frac{3}{8}$$
$8$ раскладывается на множители $2, 2$ и $2$, значит, у нас получится перевести дробь с этим знаменателем в десятичную.
Теперь найдём дополнительные множители. Для этого нам нужно разделить желаемый знаменатель на $8$. Помним, что нам нужно, чтобы в знаменателе было «круглое» число — $10, 100, 1000$ и т.п.
Конечно, мы не можем поделить $10$ на $8$ без остатка. $100$ на $8$ также не делится без остатка, поэтому делим $1000$ на $8$, у нас получается $125$.
$$5\frac{3}{8} = 5\frac{3 \cdot 125}{8 \cdot 125} = 5\frac{375}{1000} = 5.375$$
{"questions":,"answer":}},"step":1,"hints":}]}
Использование калькулятора при переводе обыкновенных дробей десятичные
Если мы пользуемся делением при переводе обыкновенной дроби в десятичную, можно использовать калькулятор для быстрых и точных подсчётов. Просто делим числитель на знаменатель и записываем получившуюся дробь. Не забывайте, что в случае смешанных чисел целая часть дроби остаётся без изменений.
Давайте попробуем.
{"questions":}]}
Но иногда и калькулятор не помогает перевести дробь в десятичный формат. Тогда нам на помощь приходит округление.
{"questions":},{"content":"Соедините обыкновенные дроби с соответствующими десятичными. Постарайтесь выполнить вычисления устно, можно пользоваться рисунком 3.`matcher-6`","widgets":{"matcher-6":{"type":"matcher","labels":,"items":}},"hints":},{"content":"Переведите дробь $\\frac{1}{50}$ в десятичную (лучше всего использовать умножение). Вычислите пример устно, не приводя к общему знаменателю, и выберите правильный ответ. <br />$\\frac{1}{50} + \\frac{1}{5}$`choice-35`","widgets":{"choice-35":{"type":"choice","options":,"answer":}},"step":1,"hints":["Чтобы перевести $\\frac{1}{50}$ в десятичную при помощи умножения, подберём дополнительный множитель, который позволит нам написать в знаменателе дроби $100$. Для этого разделим $100$ на $50$, получится $2$.","Умножим числитель и знаменатель дроби $\\frac{1}{50}$ на $2$. У нас получится $\\frac{2}{100}$. Эту дробь можно записать как $0.02$.","Чтобы вычислить $\\frac{1}{5}$, разделим $1$ на $5$. <br />$1 : 5 = 0.2$","Осталось только выполнить сложение.<br />$0.2 + 0.02 = 0.22$"]}]}
Способы преобразования дроби в число
Первый способ, как перевести дробь в число годится для дроби, которую можно преобразовать в число, являющееся десятичной дробью. Сначала выясним, можно ли перевести заданную дробь в дробь десятичную
Для этого обратим внимание на знаменатель (цифра, которая под чертой или справа от наклонной). Если знаменатель можно разложить на множители (в нашем примере — 2 и 5), которые могут повторяться, то данную дробь реально преобразовать в конечную десятичную дробь
Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Второй способ, как перевести дробь в число — более простой: необходимо числитель поделить на знаменатель. Для применения этого способа просто произведем деление, а полученное число и будет той искомой десятичной дробью. Например, надо перевести дробь 2/15 в число. Делим 2 на 15. Получаем 0, 1333… — бесконечная дробь. Записываем так: 0,13(3). Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
Самый простой способ по переводу дроби в число — это использование калькулятора или иного вычислительного прибора. Укажем сначала числитель дроби, потом нажмем кнопку со значком «разделить» и набираем знаменатель. После нажатия клавиши «=» мы получаем искомое число.
Десятичные числа, такие как 0,2; 1,05; 3,017 и т.п. как слышатся, так и пишутся. Ноль целых две десятых, получаем дробь . Одна целая пять сотых, получаем дробь . Три целых семнадцать тысячных, получаем дробь . Цифры до запятой в десятичном числе — это целая часть дроби. Цифра после запятой — числитель будущей дроби. Если после запятой однозначное число — в знаменателе будет 10, если двухзначное — 100, трехзначное — 1000 и т.д. Некоторые полученные дроби можно сократить . В наших примерах
Как перевести десятичную дробь в обыкновенную дробь
Перевод десятичной дроби в обыкновенную — это простой процесс. В числителе дроби записывается число, которое следует за запятой, а в знаменателе ставится разрядная единица, содержащая такое же количество нулей, сколько знаков после запятой в исходной дроби. Например, если нужно перевести десятичную дробь 0,625 в обыкновенную, в числителе будет записано число 625, а в знаменателе — число, содержащее два нуля, то есть 100. Получится дробь 625/1000, которую можно сократить до 5/8. Таким образом, перевод десятичной дроби в обыкновенную — это простой математический приём, который позволяет записать десятичную дробь в виде обыкновенной и удобнее работать с ней.
Как дробь с целой частью перевести в обычную
Для того чтобы перевести смешанное число в неправильную дробь, необходимо выполнить несколько шагов. Во-первых, умножаем знаменатель дроби на целую часть числа. Затем прибавляем к этому произведению числитель дробной части. При этом знаменатель остается без изменений. Полученная сумма становится числителем неправильной дроби, а знаменатель остается тот же. Таким образом, мы успешно перевели смешанное число в обычную дробь. Например, если у нас есть число 3 1/4, необходимо умножить знаменатель дроби (4) на целую часть числа (3), что дает нам 12. Затем прибавляем числитель дробной части (1) и получаем 13. Таким образом, смешанное число 3 1/4 можно записать в виде обычной дроби 13/4.
Перевод десятичных чисел в обыкновенную дробь
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3: Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2: Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.
По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Онлайн-калькулятор на «Математическом ресурсе» Calcs.su
Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.
Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.
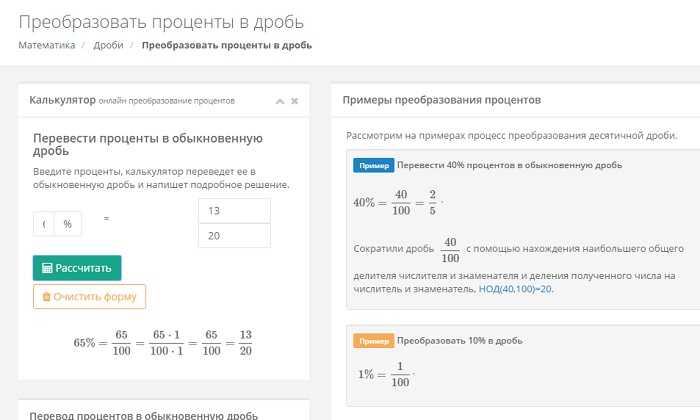
В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам. Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.
Что дальше?
Хотите узнать самые быстрые и простые способы конвертировать градусы Фаренгейта в градусы Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градусы Фаренгейта (или наоборот).
Вы изучаете логарифмы и натуральные логарифмы на уроках математики? У нас есть руководство по всем правила естественного журнала ты должен знать.
Знаете ли вы, что вода имеет особую плотность? Ознакомьтесь с нашим руководством, чтобы узнать какая плотность воды и как может измениться плотность.
Есть друзья, которым тоже нужна помощь в подготовке к экзаменам?
Десятичные дроби — коротко о главном
1. Определение
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac{8}{10},\ \frac{13}{100},\frac{49}{1000}\));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac{1}{7}=0,\underbrace{142857}_{{период}}\underbrace{142857}_{период}142…=0,\left( 142857 \right)\))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac{3}{100}=0,03=0,030=0,030000\)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
- Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
- Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа
При умножении нам неважно, стоят ли запятые под запятыми и так далее
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
Как можно перевести обыкновенную дробь в десятичную
Рассмотрим пример: дробь 3/5. Для превращения ее в десятичную, умножим числитель и знаменатель на 2: получим 6/10. Теперь мы можем записать 6/10 в виде десятичной дроби — 0,6.
Если у нас есть дробь с большим числителем или знаменателем, мы можем использовать аналогичный способ. Например, пусть у нас есть дробь 7/25. Умножим числитель и знаменатель на 4: получим 28/100. Записываем десятичную дробь — 0,28.
Таким образом, обыкновенную дробь можно перевести в десятичную путем умножения числителя и знаменателя на одно и то же число, чтобы получить в знаменателе 10, 100, 1000 и т. д. Затем записываем полученную дробь в виде десятичного числа.
Перевести обычную дробь в десятичную возможно несколькими способами
После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.
Как переводить дроби в десятичные: наиболее простой метод
Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.
Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.
Рассмотрим примеры:
Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:
После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.
Можно рассмотреть дополнительный пример, для наглядности:
Второй и боле популярный способ переводить дроби в десятичные
Второй вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.
Стоит запомнить
Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.
Рассмотрим действие на примере:
Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.
После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».
Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.
Как перевести десятичную дробь в обыкновенную: правило
В данной публикации мы рассмотрим, каким образом конечную или бесконечную десятичную дробь можно перевести в обыкновенную (простую). Также разберем решение примеров для лучшего понимания изложенного материала.
- Правило перевода десятичной дроби в обыкновенную
- Примеры
- Конечные дроби
- Бесконечные дроби
Правило перевода десятичной дроби в обыкновенную
Чтобы перевести десятичную дробь в простую, придерживаемся следующих правил:
1. Целая часть десятичной дроби – это то же самое, что и целая часть обыкновенной дроби, которая в данном случае будет являться смешанной.Примечание: если целая часть десятичной дроби равняется нулю, значит мы имеем дело с правильной простой дробью (числитель меньше знаменателя).
2. Цифры после запятой (дробная часть) в десятичной дроби пишем в числителе дробной части обыкновенной дроби. При этом, отбрасываем все нули.
3. В знаменателе дробной части простой дроби пишем единицу и количество нулей, равное количеству цифр после запятой в десятичной дроби.Примечание: Нули, которые иногда могут встречаться после цифр в дробной части десятичной дроби, не считаются (согласно основному свойству) и их можно отбросить.
Чтобы превратить бесконечную десятичную дробь в обыкновенную сначала ее следует округлить и только после этого выполнить перевод.
Для перевода бесконечных периодических десятичных дробей в простые дроби есть отдельная инструкция.
Конечные дроби
Пример 1
0,2 =
2/10
Т.к. после запятой всего одна цифра, значит пишем один ноль после единицы в знаменателе, а в числитель переносим цифру 2.
Пример 2
0,02 =
2/100
Т.к. после запятой две цифры, значит пишем два нуля после единицы в знаменателе.
Пример 3
0,02000 = 0,02 =
2/100
Т.к. нули после цифр в дробной части десятичной дроби можно отбросить, следовательно, остаются только две цифры, а значит – всего два нуля с единицей в знаменателе. Числитель, как и в примере выше, будет содержать только одну цифру 2.
Пример 4
3,8 = 3
8/10
Целую часть десятичной дроби переписываем в целую часть простой смешанной дроби, а дробную часть представляем в виде числителя и знаменателя. Полученную дробь, также, можно записать как неправильную.
3
8/10
=
3 ⋅ 10 + 8/10
=
38/10
Пример 5
6,27 = 6
27/100
(смешанная дробь)
6
27/100
=
6 ⋅ 100 + 27/100
=
627/100
(неправильная дробь)
Пример 6
8,09 = 8
9/100
(смешанная дробь)
8
9/100
=
8 ⋅ 100 + 9/100
=
809/100
(неправильная дробь)
Пример 7
10,607 = 10
607/1000
=
10 ⋅ 1000 + 607/1000
=
10607/1000
Пример 8
15,040500 = 15,0405 = 15
405/10000
=
15 ⋅ 10000 + 405/10000
=
150405/10000
Бесконечные дроби
Давайте переведем бесконечную дробь 12,004571231457668723568421… в обыкновенную.
РешениеДля начала округлим дробь до 4 цифр после запятой, т.е. 12,004571231457668723568421… ≈ 12,0046.
Теперь можем превратить эту дробь в простую.
12,0046 = 12
46/10000
=
12 ⋅ 10000 + 46/10000
=
120046/10000
Можно ли любую обыкновенную дробь перевести в десятичную
Ответ на этот вопрос — «Да». Любую обыкновенную дробь можно записать в виде конечной или бесконечной десятичной, периодической дроби. У каждой дроби всегда есть эквивалентное представление в десятичной форме.
Теперь, прежде чем вы приступите к преобразованию обыкновенной дроби в десятичную, обратите внимание на следующие полезные советы:
- Используйте калькулятор: Если у вас есть доступ к калькулятору, лучше воспользуйтесь им для выполнения деления. Это упростит и ускорит процесс.
- Округление: При округлении десятичной дроби рекомендуется использовать «четное округление», то есть округлять до ближайшего четного числа.
- Проверьте результат: После окончания преобразования проверьте результат с помощью других методов или калькулятора, чтобы убедиться в его точности.
Выводы:
Перевод обыкновенной дроби в десятичную форму может быть выполнен различными способами, включая деление числителя на знаменатель и умножение на определенное число
Независимо от выбранного подхода, важно следовать указанным шагам и быть внимательным при округлении результатов. При необходимости всегда лучше проверять результаты с помощью других методов или с использованием калькулятора, чтобы быть уверенным в их точности
Можно ли бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби
Для доказательства этого факта необходимо воспользоваться алгебраическими операциями и свойствами рациональных чисел. Первым шагом можно представить бесконечную десятичную периодическую дробь в виде обыкновенной бесконечной десятичной периодической дроби, умножив исходную дробь на 10. Затем, в результате вычислений, можно выделить две части этой периодической дроби — целую и периодическую.
Затем, используя формулы и свойства обыкновенных дробей, можно свести данную бесконечную периодическую дробь к виду обыкновенной. Если период равен нулю, то получится обыкновенная дробь без остатка, а если период не равен нулю, то бесконечную периодическую дробь можно записать в виде обыкновенной, где числитель выражен через разность между периодом и целой частью, а знаменатель равен разности между числителем и целой частью.
Таким образом, любую бесконечную десятичную периодическую дробь можно записать в виде обыкновенной дроби, что означает, что она является рациональным числом.
Как десятичную дробь прибавить к обычной дроби
Для сложения десятичных дробей необходимо следовать нескольким шагам. В начале, нужно записать оба числа одно под другим так, чтобы запятая стояла под запятой в обоих числах. Затем производится сложение чисел, при этом сложение осуществляется как обычное сложение чисел в столбик, начиная с самого правого разряда. После сложения всех разрядов, запятая в итоговом ответе будет расположена под запятой. Если в процессе сложения получилось число, у которого количество разрядов после запятой больше, чем десятичная дробь, пишется результат с штрихом на запятой и продолжается сложение следующих разрядов. Итоговая сумма будет содержать десятичную дробь, если она присутствовала в исходных числах.
Как преобразовать десятичную дробь в обыкновенную примеры
Далее мы должны упростить полученную обыкновенную дробь. Для этого умножим числитель и знаменатель на 10, пока в числителе не станет только цифры после запятой. Например, в случае с дробью 0,35 мы умножаем числитель и знаменатель на 10, получаем 3,5/10. При этом, если в какой-то момент мы получаем дробь без нулей после запятой, мы умножаем числитель и знаменатель на 1000, 10000 и так далее, чтобы убрать все цифры после запятой в числителе.
После упрощения дроби, мы можем сократить ее, если это возможно. Для этого находим наибольший общий делитель числителя и знаменателя и делим оба на него. В итоге получается обыкновенная дробь в виде a/b, где a и b — целые числа.
Как разделить обыкновенную дробь на целое число
Для того чтобы разделить обыкновенную дробь на целое число, нужно умножить знаменатель дроби на данное целое число, а числитель оставить без изменений. Например, если у нас есть дробь 3/4 и мы хотим разделить ее на число 2, мы умножаем знаменатель 4 на 2 и получаем 8. Числитель остается без изменений и равен 3. Таким образом, исходная дробь 3/4 разделяется на 2, и мы получаем дробь 3/8. Это означает, что одна часть дроби 3/4 равна 3/8. Таким образом, мы можем разделить обыкновенную дробь на целое число, умножив знаменатель на это число и оставив числитель без изменений.
Онлайн-калькулятор на «Математическом ресурсе» Calcs.su
Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.
Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.
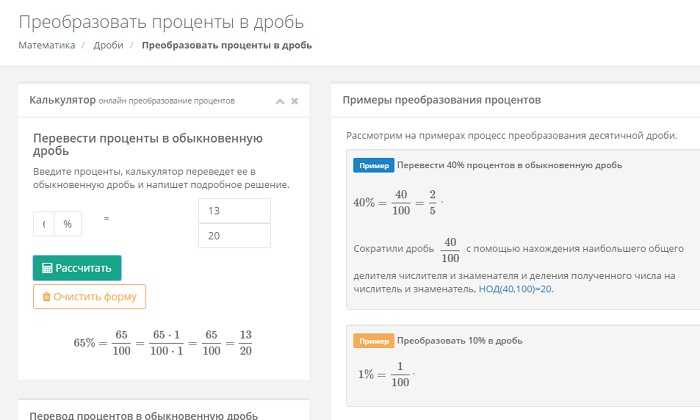
В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам. Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.





























