Дроби и действия с дробями

Действия над смешанными числами

Смешанное число — математическое выражение, в состав которого входят целая величина и обыкновенная правильная дробь. Например, 7[1/3] является смешанным, целая часть — 7 и дробная — 1/3. Последняя заключается в квадратные скобки. В смешанное выражение могут конвертироваться только целые числа и неправильные дроби.

Для каждого вида конвертации существует определенная методика. Специалисты предлагают только 2 алгоритма преобразования:

1. Целого числа.
2. Неправильной дроби.

В первом случае операция выполняется довольно просто. Однако начинающим математикам рекомендуется пока придерживаться методики. Неправильную дробь необходимо конвертировать по усложненному алгоритму при помощи специальной формулы. Последняя формирует новый числитель.

Представление целой величины

Необязательно исходным значением может быть неправильная дробь. Каждое целое число можно представить в виде смешанного при помощи такого алгоритма:

1. Записать величину.
2. Отнять от целой части единицу.
3. Указать в скобках дробь — единичное значение.
4. Написать результат.

Реализация методики выполняется на примере числа 7, которое нужно представить в смешанной форме. Операция выглядит таким образом:

1. Записать число: 7.
2. Величина без учета единицы: 6.
3. Дробь: 2/2.
4. Полная запись: 6[2/2].

Конвертация неправильного дробного тождества

В случае конвертации числа, представленного в виде обыкновенной дроби, необходимо воспользоваться определенным алгоритмом. Он выглядит таким образом:

1. Записать число смешанного типа.
2. Выделить целую часть.
3. Рассчитать «новый» числитель по формуле: Q’=Q-C*Z, где Q — искомая величина числителя, C — целое число и Z — знаменатель.
4. Результат: Q’/Z.

Реализацию алгоритма нужно разобрать на примере «78/7» для закрепления теоретических знаний. Решать его нужно следующим образом:

1. Записать значение: 78/7.
2. Выделить целое значение (часть): 78/7=11.
3. Найти величину нового числителя: 78−11*7=1, где 78 — числитель искомой неправильной дроби, 7 — ее знаменатель и 11 — целая часть.
4. Написать результат: 11[1/7].

Специалисты рекомендуют на начальных этапах обучения четко следовать методике. Со временем надобность в ней исчезнет, поскольку операция преобразования будет выполняться на автоматизме. Далее необходимо разобрать алгоритм обратной конвертации.

Обратная операция

Для проверки правильности конвертации неправильной дроби в смешанное число или решения задач необходимо воспользоваться специальным алгоритмом. Он имеет следующий вид:

1. Записать смешанное тождество.
2. Вычислить величину нового числителя: Q=Q’+C*Z, где Q’ — исходная величина числителя, C — целое значение и Z — знаменатель.
3. Записать результат: Q/Z.

Чтобы понять принцип работы алгоритма, необходимо разобрать пример 11[1/7]. Он должен решаться таким способом:

1. Написать смешанное тождество: 11[1/7].
2. Числитель: 11*7+1=78.
3. Искомый результат: 78/7.

При помощи этого алгоритма можно осуществлять операцию преобразования в целое число.

Таким образом, смешанное число — вид дробного выражения, которое применяется при решении задач. Для его конвертации необходимо знать соответствующие методики.

Деление обыкновенных дробей

Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.

Если необходимо произвести деление обыкновенной дроби a b на c d , тогда для определения такого числа нужно произвести умножение на делитель c d , это даст в итоге делимое a b . Получим число и запишем его a b · d c , где d c является обратным c d числу. Равенства можно записать при помощи свойств умножения, а именно: a b · d c · c d = a b · d c · c d = a b · 1 = a b , где выражение a b · d c является частным от деления a b на c d .

Отсюда получим и сформулируем правило деления обыкновенных дробей:

Чтобы разделить обыкновенную дробь a b на c d , необходимо делимое умножить на число, обратное делителю.

Запишем правило в виде выражения: a b : c d = a b · d c

Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.

Перейдем к рассмотрению деления обыкновенных дробей.

Выполнить деление 9 7 на 5 3 . Результат записать в виде дроби.

Число 5 3 – это обратная дробь 3 5 . Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 9 7 : 5 3 = 9 7 · 3 5 = 9 · 3 7 · 5 = 27 35 .

Ответ: 9 7 : 5 3 = 27 35 .

При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.

Разделить 8 15 : 24 65 . Ответ записать в виде дроби.

Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15 : 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9

Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9

Выделяем целую часть и получаем 13 9 = 1 4 9 .

Ответ: 8 15 : 24 65 = 1 4 9 .

Дробные выражения

Когда ученик видит в учебнике задание в виде выражения: 

то желание заниматься математикой сразу пропадает. Сегодня мы узнаем,как решать дробные выражения и докажем, что даже такие выражения совершенно не сложные, и выполнить вычисления сможет каждый желающий после изучения нашего урока!

Никого не пугает запись обыкновенной дроби – 3/7, 4/15, 8/14.

Каждый понимает, что дробная черта заменяет привычный знак деления – : .

Например:

10/21 = 10 : 21 или 7/18 = 7 : 18.

Выходит, что частное чисел или выражений, в случае замены знака деления чертой дроби, называют дробным выражением.

Вот так, проведя два простых вычисления, мы выполнили задание, вызывающее недоумение у школьников. Математика интересная и простая наука. Если приложите немного внимания и терпения, то результат не заставит себя ждать!

Знаешь ли ты?

1) Ученые – селекционеры вывелиновый вид яблонь. Удивительным является то, что корни растения уходит в землю более чем на 49/50километра (около 980 метров), а общая длина корневища достигает 4000 метров.

2) За всю жизнь человек выпивает примерно 75 тонн воды. Подсолнечнику, например, достаточно 1/4 тонны(250 литров), чтобы вырасти и принести семена.

3) Италия в который раз удивила весь мир. Около вулкана Этна растет каштан, диаметр ствола которого, составляет,3/50 километра (около 60 метров),это чуть ли не половина футбольного стадиона.

4) Пальма Рафия Тедигера встречается только в Бразилии. Она интересна тем, что её листья имеют гигантские размеры. Черенок листка достигает1/200 километра (5 метров), длина листика – более1/50 километра (более 20 метров), ширина – более 5 метров (1/200 километра).

Смешанные дроби 5 класс

Пятиклашки любят называть такие дроби не смешанные, а <<смешные>>, наверное так легче запомнить. Смешанные дроби называются так от того, что они получились путем соединения целого натурального числа  и обыкновенной дроби.

Смешанная дробь состоит из целой и дробной части.

При чтении таких дробей сначала называют целую часть, затем дробную: одна целая две третьих, две целых одна пятая, три целых две пятых, четыре целых три четвертых.

Как же они получаются, эти смешанные дроби? Все довольно просто. Когда мы получаем в ответе неправильную дробь ( дробь у которой числитель больше знаменателя), мы ее должны всегда переводить в смешанную. Достаточно разделить числитель на знаменатель. Это действие называется выделением целой части:

Перевести смешанную дробь обратно в неправильную тоже несложно:

Признаки делимости

При сокращении дробей следует знать признаки делимости. Если одно число делится на другое, то результатом является третья величина, которая называется частным значением. Первое число называется делимым, второе — делителем. Признаки деления на них от 1 до 9 (соответствуют пунктам нумерации):

1. Любое число.
2. Последняя цифра — четная величина.
3. Сумма делится на тройку.
4. Две крайние справа цифры (последние) делятся на четверку.
5. Последняя цифра заканчивается на нуль или пятерку.
6. Сумму, полученную при сложении компонентов-цифр числа, можно делить на двойку и тройку.
7. Деление по формуле / 7, где m, n и t — единицы, десятки и сотни искомого числа.
8. Деление на двойку и четверку на основании пунктов 2 и 4.
9. Алгебраическая сумма цифр, составляющих число, делится на девятку без остатка.

Признаки делимости рекомендуется заготовить в виде электронной презентации или на картонном листе. Математики рекомендуют их выучить, поскольку это позволит существенно сократить время на решение примеров и задач.

Деление дроби на число

Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?

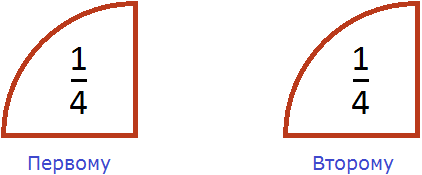
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет  пиццы. Значит каждому достанется по  пиццы.

Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.

Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.

Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.

Итак, требуется разделить дробь  на число 2. Здесь делимым является дробь , а делителем число 2.

Чтобы разделить дробь  на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить  на 

Получили ответ . Значит при делении половины на две части получается четверть.

Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:

Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:

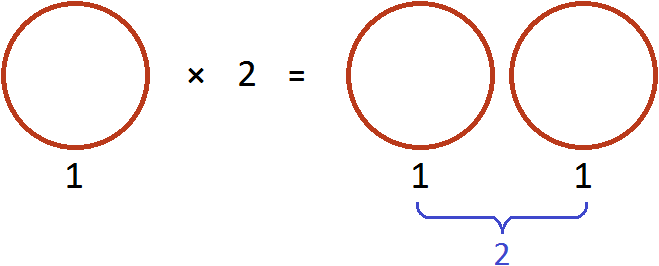
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:

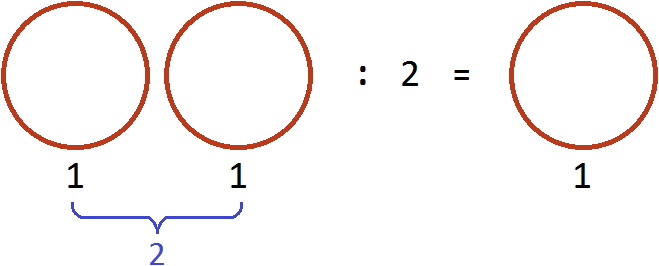
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь 

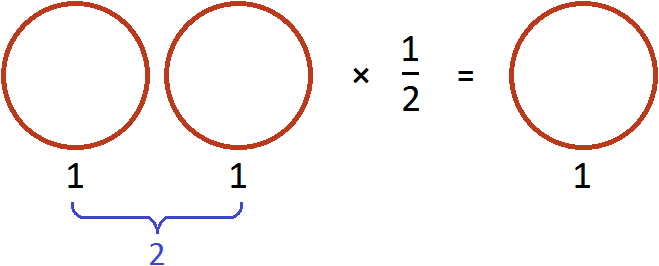
В обоих случаях получился один и тот же результат.

Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить  на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь 

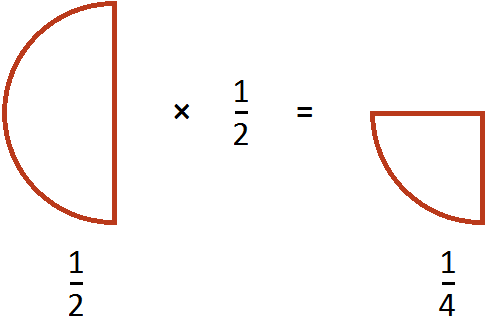
Пример 2. Найти значение выражения 

Умножим первую дробь на число, обратное делителю:

Допустим, имеется четверть пиццы и нужно разделить её на двоих:

Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:

Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5

10 : 2 = 5

Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь 

Как видно результат не изменился. Мы снова получили ответ 5.

Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.

Пример 3. Найти значение выражения 

Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь 

Допустим, имелось  пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков

Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении  на 6 получается 

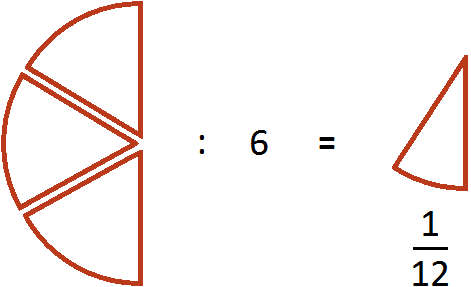
История дробей

Русское слово «дробь», как и его аналоги в других языках, происходит от латинского слова «fractura» с арабским происхождением и означает в переводе: ломать или дробить. Основы теории обыкновенных дробей заложили греческие и индийские математики. Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.

Позже дроби появляются в Европейской математике, например, у Фибоначчи в 1202 году. Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).

В России, начиная с древней Руси, дроби именовали долями. А в первых отечественных учебниках по математике дроби назывались ломаными числами. Термин «дробь», как аналог латинского «fractura», впервые используется в «Арифметике» Магницкого в 1703 году как для обыкновенных, так и для десятичных дробей.

Как научить ребенка легко решать дроби с помощью лего

С помощью такого конструктора можно не только хорошо развивать воображение ребенка, но и объяснить наглядно в игровой форме, что такое доля и дробь.

На картинке ниже показано, что одна часть с восемью кружками это целое. Значит, взяв пазл с четырьмя кружками, получается половина, или 1/2. На картинке наглядно показано, как решать примеры с лего, если считать кружки на деталях.

Вы можете построить башенки из определенного количества частей и подписать каждую из них, как на картинке ниже. Например возьмем башенку из семи частей. Каждая часть зеленого конструктора будет 1/7. Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.

Нахождение целого числа по дроби

Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.

А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.

Например, если  длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.

Требуется найти длину всей линейки по дроби . Известно, что  длины всей линейки составляют 6 см.

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби  это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби  это число 2.

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:

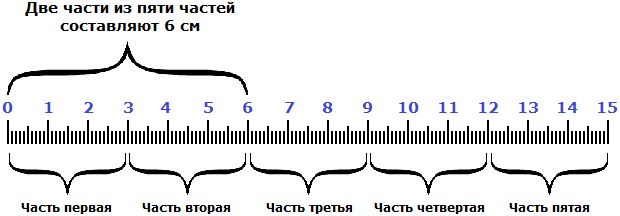
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2

6 см : 2 = 3 см

Итак, мы нашли длину одной части. Одна часть из пяти или  длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5

3 см × 5 = 15

Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.

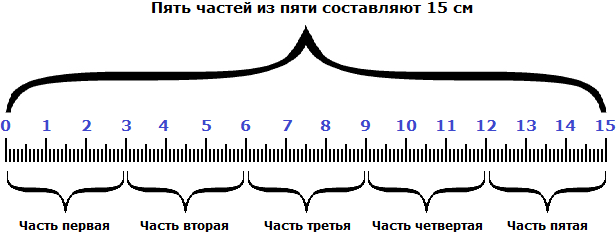
Видно, что пять частей из пяти или  составляют пятнадцать сантиметров.

Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:

Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.

Пример 2. Число 20 это  от всего числа. Найдите это число.

Знаменатель дроби  показывает, что число, которое мы должны найти, разделено на пять частей. Если  этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти  (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби

20 : 4 = 5

Мы нашли  от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби

5 × 5 = 25

Мы нашли  от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.

Пример 3. Десять минут это  времени приготовления каши. Найдите общее время приготовления каши.

Знаменатель дроби  показывает, что общее время приготовления каши разделено на три части. Если  времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти  времени приготовления. Для этого 10 нужно разделить на числитель дроби

10 мин : 2 = 5 мин

Мы нашли  времени приготовления каши.  времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби

5 мин × 3 = 15 мин

Мы нашли  времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.

Пример 4.     массы мешка цемента составляет 30 кг. Найти общую массу мешка.

Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .

30кг : 2 = 15кг

Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби

15кг × 4 = 60кг

Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.

Виды дробей

Дроби бывают нескольких видов:

• обыкновенные;
• смешанные и простые;
• правильные и неправильные;
• десятичные;
• в виде процентов.

Обыкновенная дробь

Обыкновенная дробь имеет вид a/b. Число a — здесь будет являться числителем дроби, а число b — будет знаменателем.

Примеры:

1. 1/2
2. 6/5
3. 3/1
4. 7/15

Правильные и неправильные

Правильной называется дробь, у которой числитель (модуль числителя) меньше модуля знаменателя.

Пример, правильной дроби: 3/4, так как 3<4.

Неправильная дробь, наоборот, имеет числитель, который по модулю больше чем знаменатель.

Пример, неправильной дроби: 4/3, так как 4>3.

Простые и смешанные

Простая дробь содержит только числитель и знаменатель. Например, 4/3.

Смешанная дробь содержит целое число и дробь, и понимается как сумма этого числа и дроби. Например, 1 и 1/3.

Неправильную дробь всегда можно сделать смешанной, то есть выделить в ней целые части.

Десятичная дробь

Десятичная дробь — это запись дроби, в которой знаменатель не дан в явном виде, но понимается как целое число, степень десяти (напр. 10, 100, 1000 и др).

Десятичная дробь записывается через запятую в строку таким образом, чтобы отделить дробную часть от целой части. Вот так:

• 0,7 – ноль целых и 7 десятых (7/10).
• 5,42 – пять целых и 42 сотых (42/100).
• 9,245 – девять целых и 245 тысячных (245/1000).

В виде процентов

Дробь в виде процентов — это когда при переводе десятичной дроби в проценты, ее необходимо умножить на 100. Запись производится с запятыми.

Например, 0,023 = 0,023 * 100% = 2,3%

Для того чтобы перевести проценты в десятичные дроби, следует разделить число процентов на 100.

Деление смешанного числа на дробь и дроби на смешанное число

Зная общий принцип, можете сформулировать, как происходит деление?

Показать правило

Скрыть

Опираясь на предыдущие правила, можно дать примерно такое определение:

Давайте для тренировки выполним такое упражнение: посмотрите на пример и найдите ошибку в вычислениях.

Рисунок 2. Пример с ошибкой

Показать правильный вариант

Скрыть

Хотя мы и заменяем деление дробей умножением, важно помнить, что в данном случае мы не можем свободно менять множители местами. В обратную дробь можно превращать только делитель

Правильное решение будет выглядеть так:

Рисунок 3

{"questions":,"items":}}}]}

Основное свойство дроби.

Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби. Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:

Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь. 2/3.

А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей. Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но… человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.

Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом .

Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.

Например, надо упростить выражение:

Тут и думать нечего, зачеркиваем букву «а» сверху и двойку снизу! Получаем:

Все правильно. Но реально вы поделили весь числитель и весь  знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении

и получить снова

Что будет категорически неверно. Потому что здесь весь числитель на «а» уже не делится! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов  преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!

Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё… пока сокращается, короче. Получим 3/8! Куда приятнее, правда?

Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора! Это важно на ЕГЭ, верно?

Суть дроби

Перед тем, как узнать что такое дробь, ребенок должен познакомиться с понятием доля. Здесь лучше всего подойдет ассоциативный метод.

Представьте целый торт, который поделили на несколько равных частей, допустим на четыре. Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.

Доли бывают разные, потому что, целое можно поделить на совершенно разное количество частей. Чем больше долей в целом, тем они меньше, и наоборот.

Чтобы доли можно было обозначить, придумали такое математическое понятие, как обыкновенная дробь. Дробь позволит нам записать столько долей, сколько потребуется.

Составными частями дроби являются числитель и знаменатель, которые разделены дробной чертой либо наклонной чертой. Многие дети не понимают их смысла, поэтому и суть дроби им не понятна. Дробная черта обозначает деление, здесь нет ничего сложного.

Знаменатель принято записывать снизу, под дробной чертой или справа от накл.черты. Он показывает количество долей целого. Числитель, он записывается сверху над дробной чертой или слева от накл.черты, определяет сколько долей взяли.К примеру дробь 4/7. В данном случае 7-это знаменатель, показывает, что есть всего 7 долей, а числитель 4 указывает на то, что из семи долей взяли четыре.

Основные доли и их запись в дробях:

Помимо обыкновеной, существует еще и десятичная дробь.

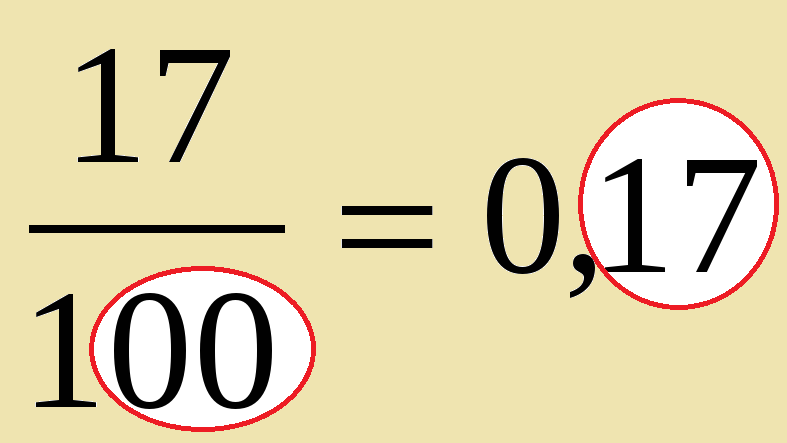
Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

1. Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.