Введение
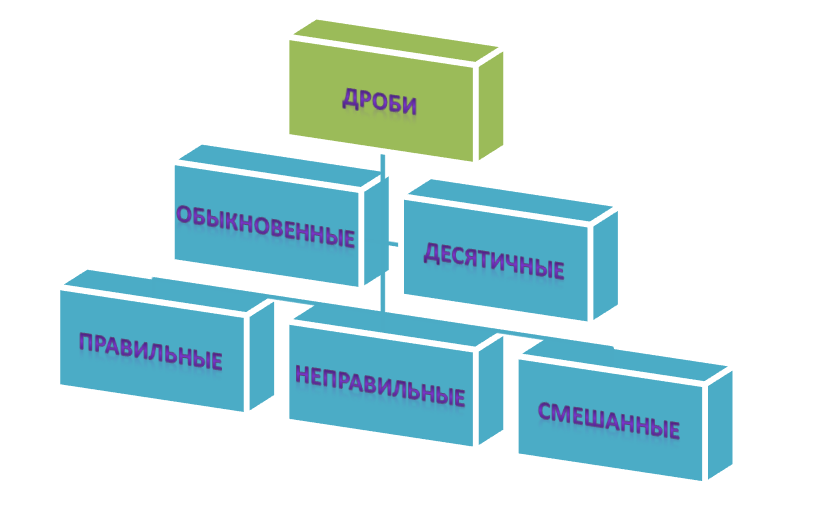
Мы уже познакомились с дробями и их видами. Давайте вспомним, какие бывают дробные числа:
Сегодня рассмотрим новый вид дробных чисел – десятичные дроби. Очень часто возникает необходимость в использовании дробных чисел, знаменатели которых имеют числовые значения 10, 100, 1000, 10000. Что такое десятичная дробь, как правильно её записывать, выполнять математические действия, именно об этом мы сегодня и поговорим.
Рассмотрим такую ситуацию:
У Маши был День Рождения, пришли гости. Праздничный торт мама разрезала на 10 кусков по количеству гостей. Какая часть торта досталась каждому гостю?
Давайте разберемся: Торт разрезан на 10 кусков, значит, знаменатель дроби равен 10, каждому достался один кусок, значит, числителем записываем единицу. Записываем как 1/10. Это числовое выражение возможно представить и в другом виде – 0,1. Такой вид числаназывается десятичной дробью. Получается, каждому досталась одна десятая доля торта.
Сформулируем определение:
Десятичная дробь – это числовое выражение, имеющее знаменатель, кратный 10. Всегда пишется в строку. Во время написания после целой части указывают только числитель. Целую и дробную части разделяет запятая.
17/100=0,17 или 3/10=0,3
18+(11/100) =18,11 или 39+(7/10)=39,7
В случае, когда дробь правильная, то перед запятой, необходимо записывать 0.
9/10=0,9
Умение записывать десятичные дроби очень помогает в решении многих математических задач.
Теперь давайте разберемся, как же обозначать десятичные дроби на координатной прямой?
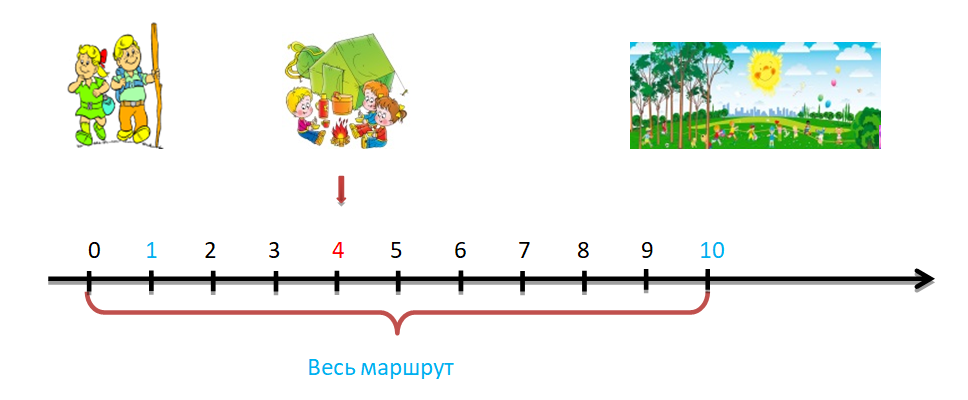
Рассмотрим ситуацию из жизни:
После окончания учебного года школьники пошли в поход. Длина маршрута составляет 10 километров. Первый привал только через 4 километра. Определите пройденную детьми часть маршрута до привала.
Чтобы ответить на главный вопрос необходимо выяснить:
- Из скольких одинаковых долей состоит весь маршрут;
- Определите числовое значение одной части всего маршрута;
- Найдите числовое значение 4 частей?
На рисунке видно, что весь маршрут разбит на 10 одинаковых частей. Одна часть пути равна 1/10 всего маршрута или 0,1. Теперь понятно, что привал будет через 4 такие части, через 4/10 или 0,4 всего пути.
А теперь давайте изобразим на координатном луче числовое выражение 4,5.
4,5 состоит из 4 целых единиц и 5 десятых доли. Значит, на координатном луче нужно отложить 4 единичных отрезка (это расстояние между началом луча и единицей), а один такой отрезок необходимо поделить на десять долей и отсчитать 5 таких частей – то есть половину.
Запомни! Всегда слева будут лежать меньшие, а справа большие числовые значения.
Десятичные дроби — коротко о главном
1. Определение
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac{8}{10},\ \frac{13}{100},\frac{49}{1000}\));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac{1}{7}=0,\underbrace{142857}_{{период}}\underbrace{142857}_{период}142…=0,\left( 142857 \right)\))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac{3}{100}=0,03=0,030=0,030000\)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
- Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
- Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа
При умножении нам неважно, стоят ли запятые под запятыми и так далее
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
Можно ли любую обыкновенную дробь перевести в десятичную
Ответ на этот вопрос — «Да». Любую обыкновенную дробь можно записать в виде конечной или бесконечной десятичной, периодической дроби. У каждой дроби всегда есть эквивалентное представление в десятичной форме.
Теперь, прежде чем вы приступите к преобразованию обыкновенной дроби в десятичную, обратите внимание на следующие полезные советы:
- Используйте калькулятор: Если у вас есть доступ к калькулятору, лучше воспользуйтесь им для выполнения деления. Это упростит и ускорит процесс.
- Округление: При округлении десятичной дроби рекомендуется использовать «четное округление», то есть округлять до ближайшего четного числа.
- Проверьте результат: После окончания преобразования проверьте результат с помощью других методов или калькулятора, чтобы убедиться в его точности.
Выводы:
Перевод обыкновенной дроби в десятичную форму может быть выполнен различными способами, включая деление числителя на знаменатель и умножение на определенное число
Независимо от выбранного подхода, важно следовать указанным шагам и быть внимательным при округлении результатов. При необходимости всегда лучше проверять результаты с помощью других методов или с использованием калькулятора, чтобы быть уверенным в их точности
Можно ли бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби
Для доказательства этого факта необходимо воспользоваться алгебраическими операциями и свойствами рациональных чисел. Первым шагом можно представить бесконечную десятичную периодическую дробь в виде обыкновенной бесконечной десятичной периодической дроби, умножив исходную дробь на 10. Затем, в результате вычислений, можно выделить две части этой периодической дроби — целую и периодическую.
Затем, используя формулы и свойства обыкновенных дробей, можно свести данную бесконечную периодическую дробь к виду обыкновенной. Если период равен нулю, то получится обыкновенная дробь без остатка, а если период не равен нулю, то бесконечную периодическую дробь можно записать в виде обыкновенной, где числитель выражен через разность между периодом и целой частью, а знаменатель равен разности между числителем и целой частью.
Таким образом, любую бесконечную десятичную периодическую дробь можно записать в виде обыкновенной дроби, что означает, что она является рациональным числом.
Как десятичную дробь прибавить к обычной дроби
Для сложения десятичных дробей необходимо следовать нескольким шагам. В начале, нужно записать оба числа одно под другим так, чтобы запятая стояла под запятой в обоих числах. Затем производится сложение чисел, при этом сложение осуществляется как обычное сложение чисел в столбик, начиная с самого правого разряда. После сложения всех разрядов, запятая в итоговом ответе будет расположена под запятой. Если в процессе сложения получилось число, у которого количество разрядов после запятой больше, чем десятичная дробь, пишется результат с штрихом на запятой и продолжается сложение следующих разрядов. Итоговая сумма будет содержать десятичную дробь, если она присутствовала в исходных числах.
Как преобразовать десятичную дробь в обыкновенную примеры
Далее мы должны упростить полученную обыкновенную дробь. Для этого умножим числитель и знаменатель на 10, пока в числителе не станет только цифры после запятой. Например, в случае с дробью 0,35 мы умножаем числитель и знаменатель на 10, получаем 3,5/10. При этом, если в какой-то момент мы получаем дробь без нулей после запятой, мы умножаем числитель и знаменатель на 1000, 10000 и так далее, чтобы убрать все цифры после запятой в числителе.
После упрощения дроби, мы можем сократить ее, если это возможно. Для этого находим наибольший общий делитель числителя и знаменателя и делим оба на него. В итоге получается обыкновенная дробь в виде a/b, где a и b — целые числа.
Как разделить обыкновенную дробь на целое число
Для того чтобы разделить обыкновенную дробь на целое число, нужно умножить знаменатель дроби на данное целое число, а числитель оставить без изменений. Например, если у нас есть дробь 3/4 и мы хотим разделить ее на число 2, мы умножаем знаменатель 4 на 2 и получаем 8. Числитель остается без изменений и равен 3. Таким образом, исходная дробь 3/4 разделяется на 2, и мы получаем дробь 3/8. Это означает, что одна часть дроби 3/4 равна 3/8. Таким образом, мы можем разделить обыкновенную дробь на целое число, умножив знаменатель на это число и оставив числитель без изменений.
Сравнение выражений
Чтобы сравнить две дроби, нужно составить уравнение из их целых частей. Если их части равные, то сравниваются десятые доли. Стоит отметить, что в этом случае учитывают разряд числа. Меньшей будет та дробь, у которой значение числа в разряде меньше.
Для того чтобы провести сравнение дробей, применяют следующую последовательность действий:
- Пробуют сократить выражения.
- Приводят дроби к одинаковому числу знаков путём дописывания в случае необходимости нулей.
- Выполняют сравнение по старшинству разрядов, начиная с целой части, а в случае равенства — с десятой, сотой и так далее.
- Если при сравнении разрядов один из них будет больше или меньше, задача считается выполненной.
Например, нужно сравнить дроби 237,4 и 238,2 и результат выразить через процентное отношение. Так как 237 меньше 238, то дробные части сравнивать уже будет не нужно. Для того чтобы определить процентное отношение, большую часть принимают за 100%, а меньшую — за X. Составляют пропорцию и делают вычисление: 237,4 * 100 = 238,2 * Х.
Это обыкновенное уравнение с одним неизвестным: Х = 237,4 * 100 / 238,2 = 99,66%. То есть первое выражение меньше второго на 100 — 99,66 = 0,34%. Десятичные выражения, как и натуральные, можно записывать в ряд, а значит, откладывать на координатной прямой. На ней правее будет стоять отношение, которое больше.
Небольшие задания решать несложно
Но существуют задачи, для решения которых нужно не только проявить максимальное внимание, но и затратить много времени. Например, как при вычислении совместных дробей
В таких случаях есть резон использовать калькулятор десятичных дробей с запятыми онлайн. Чтобы им воспользоваться, особых знаний не нужно. Загрузив сайт и введя в таблицу исходные данные, пользователю нужно всего лишь нажать кнопку «Рассчитать» и получить точный результат.
Форма записи
При записи десятичной дроби используют следующую форму: сначала пишут целую часть, затем ставят разделитель целой и дробной доли (запятую), а после уже указывают дробную составляющую. Количество цифр, идущих после запятой, зависит от размерности. Различают десятые доли, их записывают одной цифрой, сотые — двумя, тысячные — тремя и так далее.
Записанные десятичные отношения выглядят так: 6,7; 3,26; 0, 234. Их принято указывать без знаменателя. Например, 7/10 = 0,7; 32/100 = 0,32. Удобнее всего пояснить на реальном примере. Пусть есть дробь 69/10. В знаменателе стоит число десять, имеющее один ноль. Отсчитав справа налево в числителе количество знаков, соответствующих числу нулей, в этом случае один, ставят запятую. В рассматриваемом примере запись будет выглядеть как 6,9. Тут 6 — целая часть, а 9 — дробная.
С отношениями можно выполнять любые действия. Их можно складывать, вычитать, делить и умножать. Десятичные дроби — это один из видов отношений. Они соответствуют выражениям, где знаменатель определяется как 10 в степени n, а n — натуральное число, то есть возникающее при счёте естественным образом.
Виды дробей
Дробные числа используют не только в математике, но и повседневной жизни. Наиболее типичное применение — это кулинария, где приготовление еды происходит с помощью смешивания определённых частей ингредиентов между собой. В качестве примера можно привести и спортивные состязания, пошив одежды, нумерацию.
Кроме десятичных отношений, существуют ещё и другие виды дроби:
- обыкновенная (простая) — записывают как отношение двух рациональных чисел;
- правильная — это выражение, у которого значение числителя меньше знаменателя;
- неправильная — в этом случае числитель больше или совпадает по величине со знаменателем;
- смешанная — образуется из неправильных как сумма натурального числа и правильной дроби.
Есть правило, по которому легко определить, существует ли возможность преобразования. Согласно ему, обыкновенную дробь можно преобразовать в конечную десятичную лишь в том случае, если её знаменатель можно разложить на множители два и пять, которые имеют свойство повторяться. Например, 11/40, знаменатель можно представить в виде произведения 2*2*2*5, поэтому привести к десятичной её возможно. А вот 13/60 преобразовать нельзя, так как в знаменателе при разложении есть число три: 5 * 2 * 2 * 3 = 60.
Для переведения простого отношения в десятичное нужно верхнюю и нижнюю часть выражения умножить на одно и то же число, но таким образом, чтобы внизу записи появилось число, кратное десяти. Например, 7/20 = 7*5/20*5 = 35/100 = 0,35. Или такой пример: 13/40 = 13/2*2*2*5 = 13*25/40*25 = 325/1000 = 0,325.
Есть и более сложный способ приведения, но при этом используют его чаще. В основе метода лежит деление уголком. То есть выполняют просто деление числителя на знаменатель. Например, 69/200. На первом этапе следует убедиться, что дробь может быть конечной десятичной, для этого раскладывают знаменатель: 200 = 5*5*2*2*2. На втором шаге выполняют деление в столбик и получают ответ: 0,345.
Популярность второго способа связана с тем, что всё же некоторые отношения проще разделить, чем подбирать, как правильно преобразовать знаменатель. Наиболее часто встречаются следующие дроби, которые поддаются преобразованию: ½ = 0,5; ¼ = 0,25; ¾ = 0,75; 1/5 = 0,2; 1/8 = 0,125; 1/10 = 0,1. А вот такие выражения, как 1/3, 1/7, 5/6, преобразовать в десятичные числа невозможно.
Перевести обычную дробь в десятичную возможно несколькими способами
После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.
Как переводить дроби в десятичные: наиболее простой метод
Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.
Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.
Рассмотрим примеры:
Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:
После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.
Можно рассмотреть дополнительный пример, для наглядности:
Второй и боле популярный способ переводить дроби в десятичные
Второй вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.
Стоит запомнить
Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.
Рассмотрим действие на примере:
Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.
После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».
Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.
Вычитание десятичных дробей
Как видите, вычитание дробей похоже на обычное вычитание в столбик натуральных чисел. Давайте подробно разберём пример:
$$8.9-5.67$$
Рисунок 5
Сначала записываем дроби друг под другом (рисунок 5, а)
Обращаем внимание, чтобы запятая была под запятой. Также в конце дроби $8.9$ пишем $0.$ Это нужно нам для того, чтобы уравнять количество знаков после запятой в обеих дробях
Начинаем вычитание справа. Нам нужно отнять $7$ сотых от $0$ сотых, это невозможно, поэтому занимаем десяток из соседнего разряда (рисунок 5, б)
У нас получается $223$, теперь остаётся только поставить запятую, отделяющую целую часть дроби от десятых (рисунок 5, в).
Разберём ещё один пример:
$$1.2-0.8$$
Так как мы не можем вычесть $8$ из $2$ , занимаем десяток из соседнего разряда. Вычитаем $8$ из $12$. Теперь в уменьшаемом числе в разряде десятков остался $0,$ а $0 — 0 = 0$. Может быть, его и писать не стоит?
Нет, писать $0$ необходимо, ведь мы знаем, что $0$ играет очень большую роль в сохранении разрядов; если после окончания вычисления мы поймём, что он не нужен, тогда и сможем его убрать, используя главное свойство десятичной дроби.
У нас получилось $04$. Ставим запятую под запятыми.
Рисунок 6
Теперь видно, что $0$ был необходим, так как он показывает количество целых в получившейся дроби.
{"questions":[{"content":"Решите пример и запишите ответ в виде десятичной дроби <br />$7\\frac{7}{10}-2\\frac{3}{100}-3\\frac{47}{100}$<br />`input-1`","widgets":{"input-1":{"type":"input","answer":}},"step":1,"hints":}]}
Распространённые ошибки при вычитании дробей те же: неправильная запись чисел, при которой запятая смещается
Необходимо помнить, что место разряда в десятичных дробях очень важно
{"questions":[{"content":"Найдите закономерность и запишите следующее число<br />$5.34 ; 7.56 ; 9.78 …$<br />`input-1`","widgets":{"input-1":{"type":"input","answer":"11.98"}},"step":1,"hints":["Чтобы вычислить закономерность, вычислим, сколько будет $7.56-5.34$. У нас получится $2.2$","Проверяем: <br />$7.56 + 2.2 = 9.78$<br />Значит, мы нашли закономерность верно.","Теперь произведём вычисление: <br />$9.78 + 2.2 = 11.98$"]},{"content":"Решите уравнения и совместите с соответствующим значением $x$.`matcher-12`","widgets":{"matcher-12":{"type":"matcher","labels":,"items":}}},{"content":"Расстояние от дома до школы $1.78$ км, а расстояние от дома до детской площадки, которая находится по пути к школе – $0.9$ км. Каково расстояние от детской площадки до школы? `input-27`","widgets":{"input-27":{"type":"input","answer":"0.88"}}}]}
Общие принципы вычитания десятичных дробей
По своей сути вычитание конечных десятичных дробей и бесконечных периодических десятичных дробей представляет вычитание соответствующих обыкновенных дробей. Действительно, указанные десятичные дроби являются десятичной записью обыкновенных дробей, о чем сказано в статье перевод обыкновенных дробей в десятичные дроби и обратно.
Рассмотрим примеры вычитания десятичных дробей, отталкиваясь от озвученного принципа.
Пример.
Выполните вычитание из десятичной дроби 3,7 десятичной дроби 0,31.
Решение.
Так как 3,7=37/10 и 0,31=31/100, то . Так вычитание десятичных дробей свелось к : . Полученную дробь представим в виде десятичной дроби: 339/100=3,39.
Ответ:
3,7−0,31=3,39.
Заметим, что вычитание конечных десятичных дробей удобно проводить столбиком, об этом методе мы поговорим в .
Сейчас разберем пример вычитания периодических десятичных дробей.
Пример.
Отнимите от периодической десятичной дроби 0,(4) периодическую десятичную дробь 0,41(6).
Решение.
Осуществим :
Таким образом, .
При необходимости можно полученную :
Ответ:
0,(4)−0,41(6)=0,02(7).
Осталось озвучить принцип вычитания бесконечных непериодических дробей.
Вычитание бесконечных непериодических дробей сводится к вычитанию конечных десятичных дробей. Для этого вычитаемые бесконечные десятичные дроби округляют до некоторого разряда, обычно, до самого младшего из возможных (смотрите округление чисел).
Пример.
Проведите вычитание конечной десятичной дроби 0,52 из бесконечной непериодической десятичной дроби 2,77369….
Решение.
Округлим бесконечную непериодическую десятичную дробь до 4 знака после запятой, имеем 2,77369…≈2,7737. Таким образом, 2,77369…−0,52≈2,7737−0,52. Вычислив разность конечных десятичных дробей, получаем 2,2537.
Ответ:
2,77369…−0,52≈2,2537.
Сложение и вычитание
При необходимости сложить или отнять от одного дробного числа другое, нужно пользоваться тем же алгоритмом действий, как и при вычитании/сложении двух чисел столбиком, с некоторой разницей касательно записи нулей. Понять, как вычитать десятичные дроби столбиком, несложно.
Например, если необходимо от «14,635» отнять «7,12», то нужно записать 7 под 4. Под 5 ничего нет, так как у второго числа только 2 знака после запятой. В таком случае дописывают 0, так как у дробного числа нули, дописанные после знака запятой, ничего не «весят» и не меняют число.
Следующий шаг — вычесть эти 2 числа друг из друга столбиком, как если бы это были обычные числа. В конкретном примере ответом будет «7,515». Сложение происходит по тому же принципу — записать числа друг под другом относительно запятой и добавить в конце нули, если необходимо. Если в задаче требуется сложить положительное и отрицательное число, это по сути вычитание и нужно руководствоваться соответствующими правилами.
Нужно также знать, как из натурального числа вычесть десятичную дробь. Найти такую разность несложно. Опять же, проще всего это сделать в столбик. Пример — вычесть из 6 1,24. У второго числа после запятой находиться 2 символа. Значит, нужно написать запятую и добавить 2 нуля первому — «6,00». Это не влияет на размер, но позволяет «минусовать» от натурального числа дробное. Ответом будет 4,76.
Разряды в десятичных дробях
В записи десятичной дроби значение каждой цифры зависит от ее позиции. Т.е. в десятичных дробях также имеет место понятие разряда.
Разряды в десятичных дробях до десятичной запятой называются так же, как и разряды в натуральных числах. Разряды в десятичных дробях после запятой вынесены в таблицу:
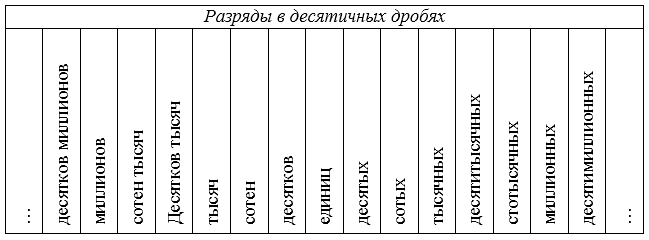Рисунок 1.
Пример 3
Например, в десятичной дроби $56,328$ цифра $5$ стоит в разряде десятков, $6$ — в разряде единиц, $3$ — в разряде десятых, $2$ — в разряде сотых, $8$ — в разряде тысячных.
Разряды в десятичных дробях различают по старшинству. При чтении десятичной дроби движутся слева направо — от старшего разряда к младшему.
Пример 4
Например, в десятичной дроби $56,328$ старшим (высшим) разрядом является разряд десятков, а младшим (низшим) — разряд тысячных.
Десятичную дробь можно разложить по разрядам аналогично разложению по разрядам натурального числа.
Пример 5
Например, разложим по разрядам десятичную дробь $37,851$:
$37,851=30+7+0,8+0,05+0,001$
Десятичная запись дробного числа
Дробное число можно представить в виде десятичной записи дробного числа.
Десятичная запись дробного числа представляет собой набор двух и более цифр от $0$ до $9$, между которыми находится так называемая \textit{десятичная запятая}.
Пример 1
Например, $35,02$; $100,7$; $123 \ 456,5$; $54,89$.
Крайняя левая цифра в десятичной записи числа не может быть нулем, исключением является только случай, когда десятичная запятая стоит сразу после первой цифры $0$.
Пример 2
Например, $0,357$; $0,064$.
Часто десятичную запятую заменяют десятичной точкой. Например, $35.02$; $100.7$; $123 \ 456.5$; $54.89$.