Умножение десятичных дробей: правила, примеры

Как перевести обыкновенную десятичную дробь

Для этого нужно разделить числитель дроби на знаменатель. Например, если у нас есть дробь 3/4, то мы делим 3 на 4 и получаем результат 0.75. Если же у нас есть дробь 5/8, то делим 5 на 8 и получаем результат 0.625. Таким образом, десятичное представление обыкновенной десятичной дроби получается путем деления числителя на знаменатель. В случае, если результат деления будет оканчиваться на бесконечную десятичную дробь, то используется приближенное значение с определенным количеством знаков после запятой

Важно помнить, что при переводе дроби в десятичное представление мы получаем число, которое может быть бесконечной десятичной дробью или иметь ограниченное количество знаков после запятой

Умно­жить на 100 зна­чит сдви­нуть за­пя­тую впра­во на две по­зи­ции.

После сдви­га можно об­на­ру­жить, что после за­пя­той уже нет цифр, а это зна­чит, что дроб­ная часть от­сут­ству­ет. Тогда и за­пя­тая не нужна, число по­лу­чи­лось целое.

При­мер 2

Сдви­гать нужно на 4 по­зи­ции впра­во. Но цифр после за­пя­той всего две. Стоит вспом­нить, что для дроби 56,14 есть эк­ви­ва­лент­ная за­пись.

Те­перь умно­жить на 10 000 не со­став­ля­ет труда:

Если не очень по­нят­но, по­че­му можно до­пи­сать два нуля к дроби в преды­ду­щем при­ме­ре, то до­пол­ни­тель­ное видео по ссыл­ке смо­жет по­мочь в этом.

Эк­ви­ва­лент­ные де­ся­тич­ные за­пи­си

За­пись 52 озна­ча­ет сле­ду­ю­щее:

Если впе­ре­ди по­ста­вить 0, по­лу­чим за­пись 052. Эти за­пи­си эк­ви­ва­лент­ны.

Можно ли по­ста­вить два нуля впе­ре­ди? Да, эти за­пи­си эк­ви­ва­лент­ны.

Те­перь по­смот­рим на де­ся­тич­ную дробь:

Если при­пи­сать ноль, то по­лу­ча­ет­ся:

Эти за­пи­си эк­ви­ва­лент­ны. Ана­ло­гич­но можно при­пи­сать несколь­ко нулей.

Таким об­ра­зом, к лю­бо­му числу можно при­пи­сать несколь­ко нулей после дроб­ной части и несколь­ко нулей перед целой ча­стью. Это будут эк­ви­ва­лент­ные за­пи­си од­но­го и того же числа.

При­мер 3

Так как про­ис­хо­дит де­ле­ние на 100, то необ­хо­ди­мо сдви­нуть за­пя­тую на 2 по­зи­ции влево. Слева от за­пя­той не оста­лось цифр. Целая часть от­сут­ству­ет. Такую за­пись часто ис­поль­зу­ют про­грам­ми­сты. В ма­те­ма­ти­ке же, если целой части нет, то ста­вят ноль вме­сто нее.

При­мер 4

Сдви­гать нужно влево на три по­зи­ции, но по­зи­ций всего две. Если перед чис­лом на­пи­сать несколь­ко нулей, то это будет эк­ви­ва­лент­ная за­пись.

То есть при сдви­ге влево, если цифры кон­чи­лись, необ­хо­ди­мо вос­пол­нить их ну­ля­ми.

При­мер 5

В дан­ном слу­чае стоит пом­нить, что за­пя­тая все­гда стоит после целой части. Тогда:

Как разделить число на десятичную дробь

Бывают дроби другого вида – десятичные. Деление на них происходит по совсем другому алгоритму. Если вы столкнулись с таким примером, то придерживайтесь инструкции:

• Для начала, превратите оба числа в десятичные дроби. Сделать это просто: делитель у вас и так представлен в виде дроби, а делимое натуральное число вы отделяете запятой, получая десятичную дробь. То есть, если делимое было числом 5, вы получаете дробь 5,0. Отделять число нужно на столько цифр, сколько стоит после запятой и делителя.
• После этого, обе десятичные дроби вы должны сделать натуральными числами. Сперва, вам покажется это немного запутанным, но это самый быстрый способ деления, который будет занимать у вас секунды, после нескольких тренировок. Дробь 5,0 станет числом 50, дробь 6,23 будет 623.
• Выполните деление. Если числа получились большие, либо деление будет происходить с остатком, выполните его в столбик. Так вы наглядно увидите все действия данного примера. Вам не нужно специально ставить запятую, так как она сама появится в процессе деления в столбик.

Данный вид деления изначально кажется слишком запутанным, так как вам нужно превратить делимое и делитель в дробь, а потом снова в натуральные числа. Но после недолгой тренировки, вы сразу станете видеть те числа, которые нужно просто разделить друг на друга.

Помните, что умение правильно делить дроби и целые числа на них могут ни раз пригодиться в жизни, поэтому, знать эти правила и простые принципы ребенку нужно идеально, чтобы в более старших классах они не стали камнем преткновения, из-за которого ребенок не может решать более сложные задачи.

I.
Чтобы разделить десятичную дробь на натуральное число, нужно делить дробь на это число, как делят натуральные числа и поставить в частном запятую тогда, когда закончится деление целой части.

Примеры.

Выполнить деление
: 1)
96,25 5; 2)
4,78 4; 3)
183,06 45.

Решение.

Пример
1)
96,25 5.

Делим «уголком» так, как делят натуральные числа. После того, как сносим цифру 2

(число десятых — первая цифра после запятой в записи делимого 96,2

5), в частном ставим запятую и продолжаем деление.

Ответ
: 19,25.

Пример
2)
4,78 4.

Делим так, как делят натуральные числа. В частном поставим запятую сразу, как снесем 7

— первую цифру после запятой в делимом 4,7

8. Продолжаем деление дальше. При вычитании 38-36 получаем 2, но деление не окончено. Как поступаем? Мы знаем, что в конце десятичной дроби можно приписывать нули — от этого значение дроби не изменится. Приписываем нуль и делим 20 на 4. Получаем 5 — деление окончено.

Ответ
: 1,195.

Пример 3)
183,06 45.

Делим как 18306 на 45. В частном поставим запятую как только снесем цифру — первую цифру после запятой в делимом 183, 6. Так же, как в примере 2) нам пришлось приписать нуль к числу 36 — разности чисел 306 и 270.

Ответ
: 4,068.

Вывод
: при делении десятичной дроби на натуральное число в частном ставим запятую
сразу после того, как сносим цифру в разряде десятых делимого

Обратите внимание: все выделенные красным цветом цифры

в этих трех примерах относятся к разряду десятых
долей делимого.. II

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.

II
. Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.

Примеры.

Выполнить деление: 1)
41,56 10; 2)
123,45 100; 3)
0,47 100; 4)
8,5 1000; 5)
631,2 10000.

Решение.

Перенос запятой влево зависит от того, сколько в делителе нулей после единицы. Так, при делении десятичной дроби на 10
мы будем переносить в делимом запятую влево на одну цифру
; при делении на 100

— перенесем запятую влево на две
цифры

; при делении на 1000

перенесем в данной десятичной дроби запятую на три цифры влево.

Что такое дробь, основные понятия и виды

Определение

Дробь — число, состоящее из нескольких равных долей.

По сути дробь — это деление одного числа на другое. Выделяют два вида: обыкновенные и десятичные.

Обыкновенная дробь — означает, состоящая из целых чисел. Обыкновенные, имею два типа записи к примеру:

• 15- разделена наклонной линией, читается как одна пятая;
• — горизонтальной линией.

Определения:

• Числитель — число, находящееся в верхней границе дроби;
• Знаменатель — число которое мы видим в нижней границе дроби.

Например: 15, где 1- числитель, 5- знаменатель. Для того чтобы проще объяснить, что такое дробь приведём простой пример. Торт разрезан на 5 кусков, если мы взяли два и них то это 25 (две пятые части торта).

Обыкновенные дроби имеют два типа правильные и неправильные.

Правильной дробью называется дробь с значениями, в которых числитель меньше знаменателя. Такое название данный тип дроби получил не зря, ведь так логичнее и правильнее, когда часть меньше целого.

Неправильная в свою очередь имеет обратные значения, когда числитель больше знаменателя.

_{Примечание. Дроби, у которых знаменатель и числитель одинаковы, тоже неправильные.}

Смешанная дробь. Существует также такое определение как смешанная дробь, такой вид, представляет собой дробь, состоящую из двух частей целой и дробной. Пример — , где четыре это целая часть, а 35 дробная. Такой тип дроби можно получить, только при делении неправильного вида дробей.

Десятичные дроби. К десятичным, относят дроби которые в знаменателе имеют 10 в натуральной степени. К примеру и тд. Такие, так же могут иметь вид строчной записи, 0,5 и 0,06. При этом в такой записи целая часть отделяется от дробной знаком запятой.

Существуют также понятия сократимой и несократимой дроби. Сократимая дробь, это та, в которой можно произвести деление числителя и знаменателя на одно и то же число.

Несократимая дробь, если такие действия выполнить нельзя.

Составная дробь, многоуровневая или выражение, имеющее несколько черт дроби. Пример

Равные и неравные дроби. Для того чтобы сказать, являются дроби равными или нет, нужно их сравнить.

Равные обыкновенные — можно вывести при помощи такого верного равенства а*b=d*c , если такое равенство не верно то данные дроби будут называться неравными.

Положительные и отрицательные дроби.

Положительные называют обыкновенные дроби, с положительными числами, при необходимость перед такими дробями ставится знак +, пример .

Отрицательными, считаются дроби со знаком минус, пример .

Стоит отметить что две дроби вида являются противоположными.

Алгебраическая дробь.

Отличается она тем, что на месте числителя и знаменателя находятся алгебраические значения, числа заменены буквами. Примеры —

Если в такой дроби буквы заменить числами, то она сразу станет обыкновенной.

Одночлен — это выражение, содержащее числа, степени положительные и их произведение. Пример:

Многочлен — это сумма одночленов. Пример: 7а+6в

Дроби на координате прямых.

Если рассматривать координату прямых, то положительные дроби на ней будут расположены справа от нулевого значения, а отрицательные слева.

Понятия и термины

Дробь — это число, в состав которого входят равные доли единиц. По сути, в математике она обозначает деление одного члена на другой. Результат действия может быть положительным или отрицательным. Классическая форма записи выглядит как x / y, где иксом называют делимое (числитель), а игреком — делитель (знаменатель). В качестве членов дробного отношения может быть не только рациональное число, но и любое выражение. Например, 67/90 (123x + 8y)/ 45z 32 / log78.

Дроби разделяют по типам. Они могут быть:

• обыкновенными — членами являются рациональные числа;
• смешанными — состоящими из суммы натурального числа и обыкновенной дроби;
• десятичными — в знаменателе записи стоит член, кратный десяти (10n).

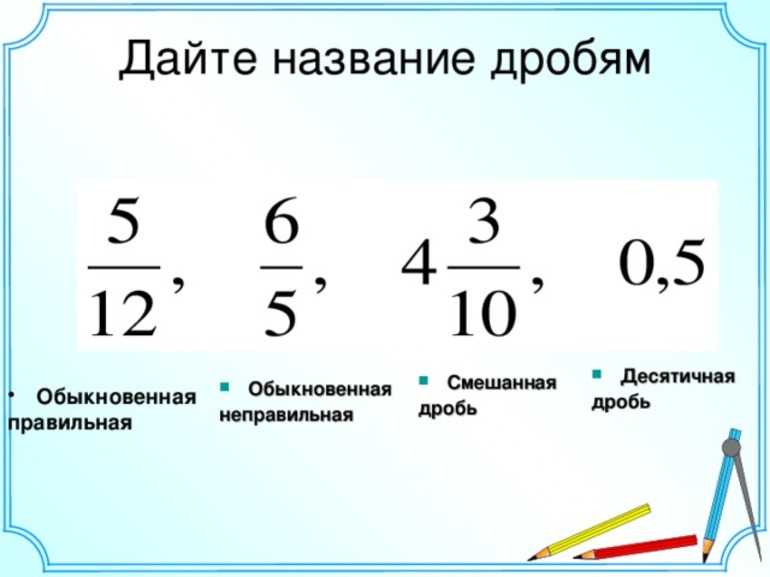
Обыкновенная дробь может быть правильной или неправильной. К какому типу она относится, зависит от величины числителя. Если делимое меньше знаменателя, то отношение правильное, а если больше, то неправильное. Отношение может быть конечным и бесконечным. Первое имеет конечное число членов после запятой, а для второго это число не определено.

Десятичное выражение, кроме классической записи с использованием горизонтальной черты, может быть записано с запятой. Например, 56/100 как 0, 56. Эти две записи равносильны. Вторая форма в некоторых случаях просто более удобная.

Перевести из одного вида в другой довольно просто. Цифры, стоящие перед запятой, относятся к целой части, а после неё — к дробной. Их ставят в числитель: 3678 = 3 678/1000. Число разрядов определяет количество нулей в знаменателе. Так, более подробная запись для рассмотренного примера будет следующей: 3678 = 3 + 6 / 10 + 7 / 100 + 8 / 1000.

С дробями можно выполнять любые арифметические действия. Их можно: складывать, вычитать, делить, умножать. При этом операции возможно выполнять как с однотипными записями, например, выполнять умножение десятичных дробей на десятичную дробь, так и разными. Правда, во втором случае приходится делать дополнительные преобразования.

Например, 2/10 = 2 * 34 / 10*34 = 68 / 340. Это важный закон, который часто позволяет заменить громоздкое трудное решение простым действием.

Как десятичную дробь умножить на целую

Для примера возьмем десятичную дробь 0.75 и натуральное число 5.

Умножаем их как натуральные числа: 0.75 * 5 = 3.75.

Затем отделяем запятую, начиная справа, на столько позиций, сколько цифр стоит в десятичной дроби. В данном случае эта позиция находится на третьем месте справа от запятой.

Таким образом, получаем конечный результат: 3.75 * 5 = 18.75.

В итоге, десятичная дробь 0.75, умноженная на натуральное число 5, равна 18.75.

Важно помнить, что при умножении десятичной дроби на целое число, её позиция в результате не изменяется — запятая всегда будет на одном и том же месте, отделяя целую часть от десятичной

Как перевести десятичную дробь в обыкновенную примеры

Далее перемножаем числитель и знаменатель на 100, чтобы избавиться от десятичной точки: 0,35/1 = 35/100. Если полученная дробь несократимая, то дробь уже является обыкновенной. Если дробь сократимая, то делим числитель и знаменатель на их наибольший общий делитель (НОД). В отношении 35/100 НОД = 5, поэтому делим числитель и знаменатель на 5 и получаем сократимую обыкновенную дробь 7/20. Таким образом, десятичная дробь 0,35 можно представить в виде обыкновенной дроби 7/20. То же самое можно сделать и с другими десятичными дробями. Например, десятичная дробь 0,75 можно перевести в обыкновенную дробь следующим образом: 0,75/1 = 75/100 = 3/4.

Решение простых примеров

Для успешного применения теории на практике нужен опыт решения различных примеров. Обычно для закрепления материала достаточно самостоятельно решить около пятнадцати заданий. Существуют различные математические сборники, в которых находятся типовые задания, предназначенные для самостоятельной проработки учащимися средней школы.

Вот некоторые из примеров на умножение десятичных дробей с решением и подробным объяснением, включённые в математические сборники:

1. Вычислить суму трёх произведений: 0, 11 * 0, 25 + 4 * 1, 67 * 8, 9 + 3, 8 * 7, 1. Решение удобнее всего выполнять по действиям. То есть сначала найти произведение каждого члена, а уже после выполнить сложение. Умножение членов будет выполняться одинаково. Вычислять произведения понадобится в столбик. Так, 0, 11 * 0, 25 необходимо умножить, не обращая внимания на запятую, то есть записать 011, а под ним 025. Получится 00275. Теперь справа налево нужно отсчитать четыре знака и поставить запятую — 0, 0275. И также можно найти произведения оставшихся двух членов. В итоге должно получиться следующее: 0, 0275 + 6, 68 + 26, 98 = 33, 6875.
2. Найти произведение: (12 / 20) * 5, 4. В этом случае удобно первый член записать в виде десятичного числа с запятой. Так дробь можно сократить на два. В итоге она примет вид: 12 / 20 = 6 / 10 = 0, 6. Теперь, используя правило умножения, несложно выполнить и нужное действие: 06 * 5, 4 = 3, 24.
3. Определить, чему равно произведение: 0, 5 * 3 4/5 * 2/5. Ответ записать в виде десятичного числа. Выражение содержит десятичную правильную и смешанную дробь. Поэтому нужно привести все члены к одному виду. Десятичное число можно представить как 5 / 10, а смешанную дробь в виде неправильной: 3 4/5 = ((3 * 5) + 4)) / 5 = 19 / 5. Теперь, по правилу умножения, все числители и знаменатели нужно перемножить между собой: 5 / 10 * 19 / 5 * 2 / 5 = (5 * 19 * 2) / (5 * 5 * 5) = 190 / 25 = 38 / 5 = (7 * 5 + 3) / 5 = 7 + 3 / 5 = 7 3/5 = 7, 6.

Общие сведения

Смешанная дробь — число, состоящее из целого значения и обыкновенного дробного выражения. Они образуются в результате операции деления. Последняя состоит из трех элементов, а именно: делимого, делителя и частного. Чтобы понять смысл смешанного числа, нужно разобрать дробные величины. К ним относятся следующие виды:

1. Обыкновенные.
2. Десятичные.

Обыкновенная дробь образуется посредством комбинации делимого и делителя, т. е. состоит всего из двух элементов. В этом случае частное имеет вид десятичного дробного тождества. Иными словами, десятичная дробь — величина, полученная при делении числителя на знаменатель.

Обыкновенные дробные выражения бывают двух видов: правильными и неправильными. У первых величина числителя меньше знаменателя, а у вторых — наоборот. Десятичные дроби делятся на 3 типа: с фиксированным количеством знаков после запятой, бесконечные периодические и непериодические.

У периодических дробных величин после запятой математические символы повторяются через определенный период, который указывается в круглых скобках. Например, число 4,(3) читается следующим образом: четыре целых и три в периоде.

Следует отметить, что бесконечные непериодические дробные выражения в их полном виде невозможно записать на листе бумаги, поскольку количество разрядов достигает бесконечности. Далее необходимо рассмотреть сокращение дробей, поскольку операция применяется для оптимизации конвертации неправильного дробного тождества в смешанное число.

Свойства дробей

Дроби, как и любые числовые выражения, обладают определенными свойствами. К ним относятся:

1. Если от числителя отнять одно значение, а затем его прибавить, дробь не изменится, т. е. (Q+T-T)/Z=Q/Z.
2. При умножении и делении на эквивалентное число величина дробного тождества не изменится, т. е. (Q*T)/(Z*Т)=Q/Z.

Первое утверждение проверить очень просто. Для этой цели нужно решить следующий пример, прибавив и отняв от числителя одно и то же значение: 7/8. Доказательство имеет такой вид:

1. Записать дробь: 7/8.
2. Взять произвольный коэффициент: 5.
3. Отнять, а затем прибавить его к числителю: (7−5+5)/8.
4. Числа «-5» и «5» являются противоположными. Их сумма равна 0, т. е. 5−5=0.
5. Если прибавить нуль к любому числу, получится искомая величина: 5+0=5.
6. Математические преобразования исходной дроби: (7−5+5)/8=/8=(7+0)/8.
7. Результат совпадает с искомым значением: 7/8=7/8.

Второе утверждение доказывается таким же простым способом на дроби ½. Для этого нужно решить пример (1*8)/(2*8) по следующему нестандартному алгоритму:

1. Записать дробное тождество: ½.
2. Коэффициент — общий множитель: 8. Последний необходимо представить в виде обыкновенной дроби: 8/8.
3. Величина «8/8» эквивалентна единице, которую можно умножить на любое число без потери значения выражения.
4. Расписать дробное значение: (½) * (8/8) = (½) * 1 = ½.
5. Сравнить результат и исходное значение: ½ = ½.
6. Утверждение доказано.

Некоторые ученики делают большую ошибку, отнимая (прибавляя) к числителю и знаменателю одну величину. Чтобы они не путали 2 утверждения сокращения, нужно привести пример и решить его:

1. Записать искомое значение: ½.
2. Коэффициент: 3.
3. Прибавить значение «3» к числителю и знаменателю: (1+3)/(2+3)=4/5.
4. Превратить искомое значение и величину в третьем пункте в десятичные дроби: 0,5 и 0,8.
5. Сравнить: 0,5 < 0,8.

Упрощение выражений

Преобразование любого арифметического выражения начинается с упрощения. Последнее применяется для уменьшения расчетов, при которых возникают ошибки. Упростить выражение — значит, сделать его более читабельным и предоставить возможность дальнейшего применения при расчетах. Иными словами, каждый результат должен «подгоняться» под мировой стандарт. Для сокращения дробей обыкновенного типа рекомендуется использовать такие правила:

1. Вынесения общего множителя за скобки и сокращение на него.
2. Формулы сокращенного умножения.
3. Приведение подобных слагаемых.

Первое правило позволяет найти единый множитель всего дробного выражения. После этого его можно будет разделить на одно и то же число. Формулы сокращенного умножения применяются также для реализации первого правила. Суть метода заключается в использовании специальных соотношений. Например, математическое выражение «1−25t 2 » выглядит таким образом: (1−5t)(1+5t).

После раскрытия скобок реализовывается третье правило — приведение подобных слагаемых. Они группируются по наличию однотипных элементов. Например, выражение 4t-4+t+t 2 −3+2t 2 имеет следующие одинаковые компоненты, которые группируются в скобках: (2t 2 +t 2 )+(4t+t)-(4+3). Если приводить подобные элементы, выражение упрощается, т. е. 3t 2 +5t-7.

Умножение десятичной дроби на натуральное число

По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.

Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.

Пример.

Вычислите произведение 15·2,27.

Решение.

Проведем умножение натурального числа на десятичную дробь столбиком:

Ответ:

15·2,27=34,05.

При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.

Пример.

Умножьте десятичную дробь 0,(42) на натуральное число 22.

Решение.

Сначала переведем периодическую десятичную дробь в обыкновенную дробь:

Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3).

Ответ:

0,(42)·22=9,(3).

А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.

Пример.

Выполните умножение 4·2,145….

Решение.

Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60.

Ответ:

4·2,145…≈8,60.

Умножение десятичной дроби на обыкновенную дробь или смешанное число

Для умножения конечной десятичной дроби или бесконечной периодической десятичной дроби на обыкновенную дробь или смешанное число, нужно десятичную дробь представить в виде обыкновенной дроби, после чего провести умножение.

Пример.

Проведите умножение десятичной дроби 0,4 на смешанное число .

Решение.

Так как 0,4=4/10=2/5 и , то . Полученное число можно записать в виде периодической десятичной дроби 1,5(3).

Ответ:

.

При умножении бесконечной непериодической десятичной дроби на обыкновенную дробь или смешанное число, обыкновенную дробь или смешанное число следует заменить десятичной дробью, после чего провести округление умножаемых дробей и закончить вычисления.

Пример.

Выполните умножение .

Решение.

Так как 2/3=0,6666…, то . После округления умножаемых дробей до тысячных, приходим к произведению двух конечных десятичных дробей 3,568 и 0,667. Выполним умножение в столбик:

Полученный результат следует округлить до тысячных, так как умножаемые дроби были взяты с точностью до тысячных, имеем 2,379856≈2,380.

Ответ:

.

Список литературы.

• Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
• Математика. 6 класс : учеб. для общеобразоват. учреждений / . — 22-е изд., испр. — М.: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Перенос запятой при делении на десятичную дробь

Хорошо, а что делать, если количество знаков после запятой в делимом и делителе разное? Например, если после переноса запятой делимое остаётся дробью?

Ничего страшного, делим дробь на натуральное число. Помните, что в этом случае нужно будет поставить в частном запятую, как только закончим делить целую часть делителя.

Например, разделим $7.04$ на $2.2$

Рисунок 5

Показать вычисления

Скрыть

Этот пример можно решить устно, не в столбик. $70$ делим на $22$, получается $3$ и $4$ в остатке. Ставим запятую после тройки, добавляем к $4$ число десятых – $4$. Теперь мы делим $44$ на $22$, у нас получается $2$.

$$7.04 : 2.2 = 3.2$$

Иногда бывает так, что знаков «не хватает». Например, нам нужно разделить 4.8 на 0.006. Как думаете, что нужно сделать в таком случае?

Показать ответ

Скрыть

Нужно дописать к делимому столько нулей, на сколько знаков нужно было бы перенести запятую.

Другими словами, мы всё равно умножаем и делимое, и делитель на одно и то же разрядное число. Если при этом приходится дописывать нули, это не делает наше вычисление ошибочным. Наоборот, если мы их не допишем, то разрядность «поедет», и ответ будет неверным.

Рисунок 6

{"questions":,"explanations":,"answer":}}}]}

Итак, деление на десятичную дробь почти не отличается от тех вычислений, что мы делали ранее

Важно только каждый раз переделывать делитель в натуральное число, умножая на разрядную единицу, и умножать делимое на то же самое разрядное число

{"questions":}},"step":1,"hints":["Вычислим значение $x$ в примере $86.4 : x = 43.2$<br />Чтобы найти делитель, нужно делимое разделить на частное. <br />$x = 86.4 : 43.2 = 864 : 432 = 2$","Вычислим значение $x$ в примере $x \\cdot 2.3 = 6.9$<br />Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. <br />$x = 6.9 : 2.3 = 69 : 23 = 3$","Вычислим значение $x$ в примере $53.4 : x = 5.34$<br />Чтобы найти делитель, нужно делимое разделить на частное. <br />$x = 53.4 : 5.34 = 5340 : 534 = 10$"]},{"content":"Соедините по парам части равенств, где $N$ и $M$ означают любые числа в пределах от $1$ до $9$. `matcher-10`","widgets":{"matcher-10":{"type":"matcher","labels":,"items":}},"step":1,"hints":["Чтобы выполнить деление на десятичную дробь, нужно умножить делимое и делитель на одну и те же разрядную единицу таким образом, чтобы делитель стал натуральным числом. <br />$0.0N : 0.M \t= (0.0N \\cdot 10) : (0.M \\cdot 10) = 0.N : M$","$0.N : 0.0M = (0.N \\cdot 100) : (0.0M \\cdot 100) =\tN0 : M$","$0.N : 0.M = (0.N \\cdot 10) : (0.M \\cdot 10) = N : M$"]},{"content":"Поезд прошёл $78$ километров за $1.3$ часа. Сколько километров он пройдёт за $2.4$ часа? `input-33`","widgets":{"input-33":{"type":"input","answer":"144"}},"step":1,"hints":["Для начала найдём скорость поезда. Для этого разделим расстояние, пройденное поездом, на время. У нас получится $78 : 1.3 = 780 : 13 = 60$","Теперь, зная скорость поезда – $60$ км/ч – мы можем легко посчитать, сколько он пройдёт за заданное время. <br />$60 \\cdot 2.4 = 144$"]}]}

Общие принципы умножения десятичных дробей

Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.

Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей . Иными словами, умножение конечных десятичных дробей
, умножение конечной и периодической десятичных дробей
, а также умножение периодических десятичных дробей
сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные .

Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.

Пример.

Выполните умножение десятичных дробей 1,5
и 0,75
.

Решение.

Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10
и 0,75=75/100
, то . Можно провести сокращение дроби , после чего выделить целую часть из неправильной дроби , а удобнее полученную обыкновенную дробь 1 125/1 000
записать в виде десятичной дроби 1,125
.

Ответ:

1,5·0,75=1,125
.

Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в .

Рассмотрим пример умножения периодических десятичных дробей.

Пример.

Вычислите произведение периодических десятичных дробей 0,(3)
и 2,(36)
.

Решение.

Выполним перевод периодических десятичных дробей в обыкновенные дроби:

Тогда . Можно полученную обыкновенную дробь перевести в десятичную дробь :

Ответ:

0,(3)·2,(36)=0,(78)
.

Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел
), после чего выполнять умножение полученных после округления конечных десятичных дробей.

Пример.

Выполните умножение десятичных дробей 5,382…
и 0,2
.

Решение.

Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38
. Конечную десятичную дробь 0,2
округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2
. Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10=
1 076/1 000=1,076
.

Ответ:

5,382…·0,2≈1,076
.

Вычитание десятичных дробей

Как видите, вычитание дробей похоже на обычное вычитание в столбик натуральных чисел. Давайте подробно разберём пример:

$$8.9-5.67$$

Рисунок 5

Сначала записываем дроби друг под другом (рисунок 5, а)

Обращаем внимание, чтобы запятая была под запятой. Также в конце дроби $8.9$ пишем $0.$ Это нужно нам для того, чтобы уравнять количество знаков после запятой в обеих дробях

Начинаем вычитание справа. Нам нужно отнять $7$ сотых от $0$ сотых, это невозможно, поэтому занимаем десяток из соседнего разряда (рисунок 5, б)

У нас получается $223$, теперь остаётся только поставить запятую, отделяющую целую часть дроби от десятых (рисунок 5, в).

Разберём ещё один пример:

$$1.2-0.8$$

Так как мы не можем вычесть $8$ из $2$ , занимаем десяток из соседнего разряда. Вычитаем $8$ из $12$. Теперь в уменьшаемом числе в разряде десятков остался $0,$ а $0 — 0 = 0$. Может быть, его и писать не стоит?

Нет, писать $0$ необходимо, ведь мы знаем, что $0$ играет очень большую роль в сохранении разрядов; если после окончания вычисления мы поймём, что он не нужен, тогда и сможем его убрать, используя главное свойство десятичной дроби.

У нас получилось $04$. Ставим запятую под запятыми.

Рисунок 6

Теперь видно, что $0$ был необходим, так как он показывает количество целых в получившейся дроби.

{"questions":[{"content":"Решите пример и запишите ответ в виде десятичной дроби <br />$7\\frac{7}{10}-2\\frac{3}{100}-3\\frac{47}{100}$<br />`input-1`","widgets":{"input-1":{"type":"input","answer":}},"step":1,"hints":}]}

Распространённые ошибки при вычитании дробей те же: неправильная запись чисел, при которой запятая смещается

Необходимо помнить, что место разряда в десятичных дробях очень важно

{"questions":[{"content":"Найдите закономерность и запишите следующее число<br />$5.34 ; 7.56 ; 9.78 …$<br />`input-1`","widgets":{"input-1":{"type":"input","answer":"11.98"}},"step":1,"hints":["Чтобы вычислить закономерность, вычислим, сколько будет $7.56-5.34$. У нас получится $2.2$","Проверяем: <br />$7.56 + 2.2 = 9.78$<br />Значит, мы нашли закономерность верно.","Теперь произведём вычисление: <br />$9.78 + 2.2 = 11.98$"]},{"content":"Решите уравнения и совместите с соответствующим значением $x$.`matcher-12`","widgets":{"matcher-12":{"type":"matcher","labels":,"items":}}},{"content":"Расстояние от дома до школы $1.78$ км, а расстояние от дома до детской площадки, которая находится по пути к школе – $0.9$ км. Каково расстояние от детской площадки до школы? `input-27`","widgets":{"input-27":{"type":"input","answer":"0.88"}}}]}