Что нужно сделать чтобы перевести обыкновенную дробь в десятичную
Для этого выбирают число на порядок больше количества цифр после запятой, так чтобы результат был целым числом. Затем числитель дроби умножают на это число, а получившееся произведение записывают в числитель. Далее знаменатель дроби также умножают на это число, а получившееся произведение записывают в знаменатель. После этого можно провести деление числителя на знаменатель и получить десятичную запись дроби. Если после выполнения деления остается остаток, то знаменатель не является степенью числа 10 и дробь не может быть точно представлена в виде десятичной. В таком случае десятичная запись будет бесконечной или периодической.
Как дробь с целой частью перевести в обычную
Для того чтобы перевести смешанное число в неправильную дробь, необходимо выполнить несколько шагов. Во-первых, умножаем знаменатель дроби на целую часть числа. Затем прибавляем к этому произведению числитель дробной части. При этом знаменатель остается без изменений. Полученная сумма становится числителем неправильной дроби, а знаменатель остается тот же. Таким образом, мы успешно перевели смешанное число в обычную дробь. Например, если у нас есть число 3 1/4, необходимо умножить знаменатель дроби (4) на целую часть числа (3), что дает нам 12. Затем прибавляем числитель дробной части (1) и получаем 13. Таким образом, смешанное число 3 1/4 можно записать в виде обычной дроби 13/4.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это от всего числа. Найдите это число.
Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
20 : 4 = 5
Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
5 × 5 = 25
Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти времени приготовления. Для этого 10 нужно разделить на числитель дроби
10 мин : 2 = 5 мин
Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби
5 мин × 3 = 15 мин
Мы нашли времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .
30кг : 2 = 15кг
Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
15кг × 4 = 60кг
Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Виды дробей
Можно выделить два больших подвида дробей:
- Обыкновенные дроби. Сюда относят числа, которые записываются через дробную черту. В таких числах всегда есть числитель и знаменатель.
- Десятичные дроби. У десятичных дробей в строку записывается числитель, а знаменатель можно определить по положению запятой. Количество знаков после запятой равняется степени, в которую нужно возвести число 10, чтобы получить знаменатель.
Смешанные числа есть как среди обыкновенных, так и среди десятичных дробей. При этом неправильной десятичной дроби быть не может. Система записи такова, что целая часть десятичной дроби выделяется автоматически.
Так знаменателем числа 0,17 является число 100, так как у дроби 2 знака после запятой. Десятичной дробь зовут за то, что знаменателем всегда выступает степень числа 10, это подразумевается самой системой записи подобных чисел.
Перевод десятичных дробей в обыкновенные дроби
Теперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби.
Перевод конечных десятичных дробей в обыкновенные дроби
Получить обыкновенную дробь, которая записана в виде конечной десятичной дроби, достаточно просто. Правило перевода конечной десятичной дроби в обыкновенную дробь
состоит из трех шагов:
- во-первых, записать данную десятичную дробь в числитель, предварительно отбросив десятичную запятую и все нули слева, если они есть;
- во-вторых, в знаменатель записать единицу и к ней дописать столько нулей, сколько цифр находится после запятой в исходной десятичной дроби;
- в-третьих, при необходимости выполнить сокращение полученной дроби.
Рассмотрим решения примеров.
Пример.
Обратите десятичную дробь 3,025
в обыкновенную дробь.
Решение.
Если в исходной десятичной дроби убрать десятичную запятую, то мы получим число 3 025
. В нем нет нулей слева, которые бы мы отбросили. Итак, в числитель искомой дроби записываем 3 025
.
В знаменатель записываем цифру 1
и справа к ней дописываем 3
нуля, так как в исходной десятичной дроби после запятой находятся 3
цифры.
Так мы получили обыкновенную дробь 3 025/1 000
. Эту дробь можно сократить на 25
, получаем .
Ответ:
.
Пример.
Выполните перевод десятичной дроби 0,0017
в обыкновенную дробь.
Решение.
Без десятичной запятой исходная десятичная дробь имеет вид 00017
, отбросив нули слева получаем число 17
, которое и является числителем искомой обыкновенной дроби.
В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4
цифры.
В итоге имеем обыкновенную дробь 17/10 000
. Эта дробь несократима, и перевод десятичной дроби в обыкновенную закончен.
Ответ:
.
Когда целая часть исходной конечной десятичной дроби отлична от нуля, то ее можно сразу перевести в смешанное число, минуя обыкновенную дробь. Дадим правило перевода конечной десятичной дроби в смешанное число
:
- число до десятичной запятой надо записать как целую часть искомого смешанного числа;
- в числитель дробной части нужно записать число, полученное из дробной части исходной десятичной дроби после отбрасывания в ней всех нулей слева;
- в знаменателе дробной части нужно записать цифру 1
, к которой справа дописать столько нулей, сколько цифр находится в записи исходной десятичной дроби после запятой; - при необходимости выполнить сокращение дробной части полученного смешанного числа.
Рассмотрим пример перевода десятичной дроби в смешанное число.
Пример.
Представьте десятичную дробь 152,06005
в виде смешанного числа
Дробь представляет собой число, которое состоит из одной или нескольких долей единицы. В математике существует три вида дробей: обыкновенные, смешанные и десятичные.
Обыкновенные дроби
Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.
Если числитель равен знаменателю или больше его, то мы имеем дело с неправильной дробью. Например: 5/5, 9/4, 5/2 При делении числителя может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим записи одного и того же числа в виде ряда различных .
Смешанные дроби
В общем виде смешанная дробь может быть представлена формулой: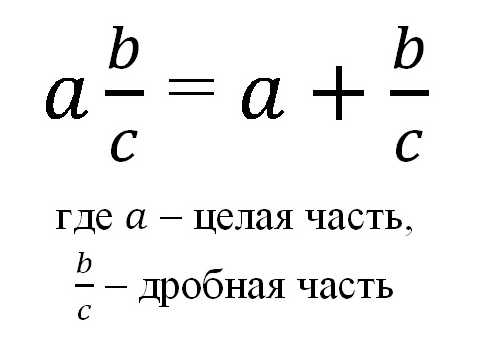
Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.
Десятичные дроби
Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.
Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом: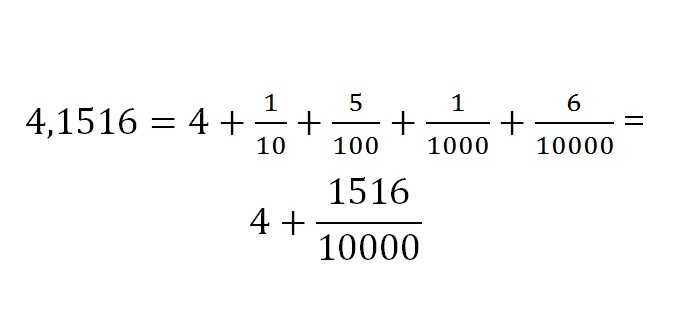
3 простых шага — Mashup Math
Готовы ли вы узнать, как преобразовать десятичную дробь в дробь ?
(и если вы хотите узнать, как преобразовать дробь в десятичную, нажмите здесь)
Прежде чем вы изучите простой способ выполнения обоих этих преобразований (с калькулятором и без него), давайте удостоверимся, что вы понять, что такое десятичные дроби и дроби:
Ключевой вывод из этих определений состоит в том, что десятичные дроби и дроби представляют собой разные способы представления одного и того же — нецелое число.
Вы можете преобразовать десятичную дробь в дробь, выполнив следующие три простых шага.
В этом случае в качестве примера вы будете использовать десятичное число 0,25 (см. рисунок ниже).
Шаг первый: Перепишите десятичное число больше единицы (в виде дроби, где десятичное число — числитель, а знаменатель — единица).
Шаг второй: Умножьте числитель и знаменатель на 10 в степени количества цифр после запятой. Если после запятой стоит одно значение, умножьте на 10, если два, то умножьте на 100, если три, то умножьте на 1000 и т. д.
В случае преобразования 0,25 в дробь после запятой идут две цифры. Поскольку 10 во 2-й степени равно 100, мы должны умножить и числитель, и знаменатель на 100 на втором шаге.
Шаг третий: Выразите дробь в простейшей (или сокращенной) форме.
Если вам нужна дополнительная помощь в упрощении дробей, посмотрите этот бесплатный видеоурок.
Выполнив эти три шага в приведенном выше примере преобразования десятичной дроби в дробь, вы можете сделать вывод, что десятичное число 0,25 при преобразовании в дробь равно 1/4.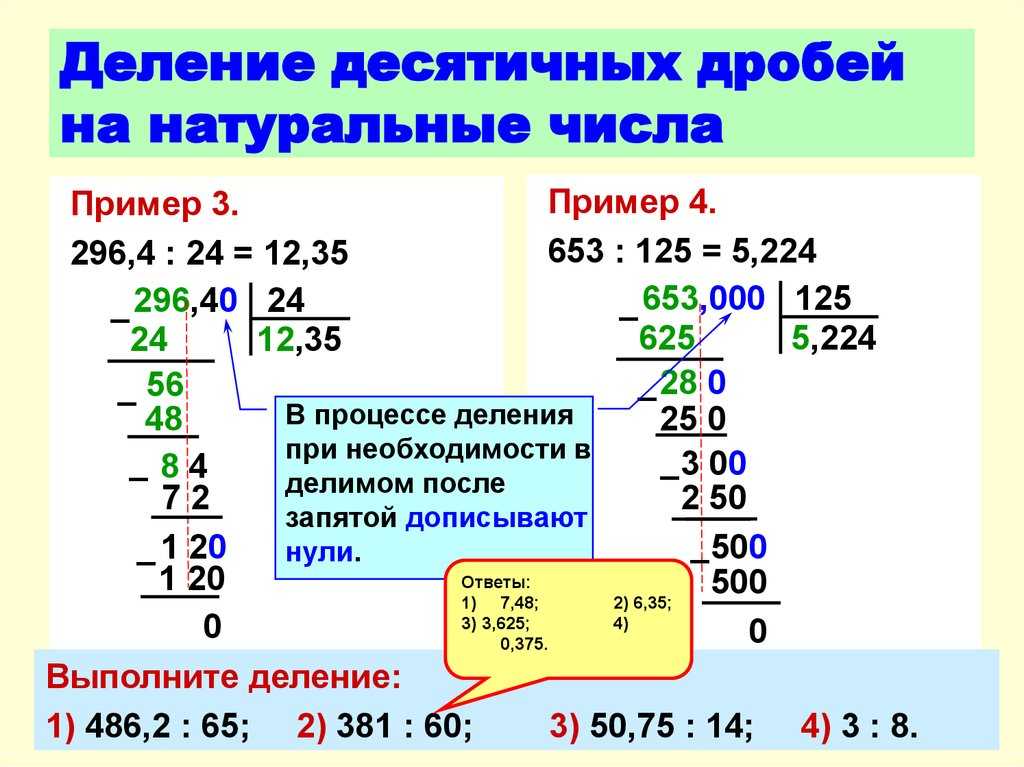
Вот еще один пример преобразования десятичной дроби в дробную:
Обратите внимание, что ответом на этот пример является смешанное число (целое число и дробь вместе взятые). Если вам нужен быстрый и простой способ преобразования десятичных чисел в дроби, вы можете воспользоваться многочисленными бесплатными онлайн-калькуляторами преобразования десятичных чисел в дроби
Если вам нужен быстрый и простой способ преобразования десятичных чисел в дроби, вы можете воспользоваться многочисленными бесплатными онлайн-калькуляторами преобразования десятичных чисел в дроби.
Этот бесплатный калькулятор десятичных дробей от www.calculatorsoup.com не только выполняет преобразование, но также показывает расчеты (используя трехэтапный метод, показанный выше), что является удобным инструментом, поскольку он не только поможет вам найти правильный ответ, но также понять процесс.
Чтобы использовать калькулятор преобразования десятичных дробей в дроби, просто введите десятичное значение и нажмите «Рассчитать».
Существует также повторяющийся калькулятор десятичной дроби (для выполнения этой функции следуйте инструкциям на веб-странице).
Вы хотите узнать больше о работе с десятичными знаками и понять разрядность? Щелкните здесь для получения дополнительных бесплатных ресурсов
Вам нужно больше практики, чтобы научиться преобразовывать десятичную дробь в дробь? Следующий рабочий лист десятичной дроби и ключ к ответу дадут вам множество возможностей применить трехэтапный процесс для преобразования десятичной дроби в дробь.
Щелкните здесь, чтобы загрузить бесплатную таблицу преобразования десятичных дробей с ответами.
И если вы ищете более подробный урок о том, как преобразовать десятичную дробь в дробную, посмотрите этот бесплатный видео-урок десятичной дроби :
Поделитесь своими идеями, вопросами и комментариями ниже!
(Никогда не пропустите блог Mashup Math — щелкните здесь, чтобы получать наш еженедельный информационный бюллетень!)
Сложение десятичных дробей
Мы знаем, что десятичная дробь состоит из целого числа и дроби. Добавляя десятичные дроби, добавляйте каждую часть отдельно.
Рассмотрим пример добавления 3.2 и 5.3. Для простоты воспользуемся столбцовым методом.
Запишем эти две дроби в столбик. При этом целая часть одной дроби должна быть меньше целой части другой. В школе это называется «запятая под запятой». Как это:
Складываем дроби: 2+3=5. Запишем пятерку в дроби ответа:
Теперь целые части равны: 3 + 5 = 8. Запишем число восемь в целой части ответа:
Целую часть от дробной отделить запятой так, чтобы запятая была ниже запятой:
Мы получили ответ: 3,2 + 5,3 = 8,5.
Что такое десятичная дробь
Десятичные дроби представляют собой целые числовые выражения, в знаменатель которых десять в какой-либо степени.
Для чего нужны десятичные дроби
- удобнее сравнивать;
- сокращение вычислений;
- удобная запись в одну строчку.
Чтобы записать десятичную дробь выполняют следующие действия:
- Отдельно написать числитель.
- Передвинуть десятичную точку на количество нулей знаменателя.
- После того, как десятичная точка сдвинулась, зачеркните нули, которые остались в конце записи.
Если на втором шаге недостаточно цифр для завершения действия, на недостающих позициях проставляются нули. Примеры десятичной записи.
\
В знаменателе первой дроби стоит 10, значит, числитель первой дроби 73 сдвинем на один знак. Получается 7,3.
Знаменатель второй дроби 100, а числитель 9. Сдвигаем десятичный знак на два знака и получаем 0,09.
Знаменатель третьей дроби 1000, а числитель 10029. Сдвигаем десятичную точку на три знака и получаем 10,029.
В последней дроби числитель 10500, перемещаем точку на три знака 10,500. Образовавшиеся в конце записи нули убираем, и получаем ответ 10,5.
Два последних примера показывают, как правильно поступать с нулями. Если нули получились справа в конце – их следует зачеркнуть, а если в середине, как в третьем примере, то их оставляем. Это цифры внутри числа.
Операции над дробями
С дробями можно совершать различные арифметические операции.
Сложение
Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.
Далее — выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.
В конце, если возможно, сократить полученную дробь.
Например:
Вычитание
Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.
Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.
Например:
Умножение
Для этого умножаются числители и записывается результат, как числитель дроби.
Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.
Например:
Деление
Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.
Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.
Например:
Сокращение
Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.
В итоге получается равную дробь, имеющая меньший знаменатель и числитель.
Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.
Значительно упростит сокращение раскладывание знаменателя и числителя на множители.
Например:
Вопросы и ответы
А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них
Какие дроби называются простыми?
Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.
Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название — десятичные.
Правильные дроби те, у которых модуль знаменателя больше модуля числителя.
Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.
Нельзя делить на 0.
Если делить на 1 — будет такое же число.
Если делить 0 на любое число, получится 0.
Когда она больше 0.
Когда перед положительной дробью ставится знак «–».
Что такое степени с дробями?
Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.
При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.
Как пользоваться калькулятором дробей?
Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.
Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор логарифмов. Вычислите онлайн натуральные, десятичные логарифмы (или с другим основанием) с решением.
- Возведение дроби в степень. Возведите онлайн любую дробь (десятичную и обыкноенную) в любую степень.
- Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
- Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
- Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
- Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
- На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
- На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.
с другой дробью, целым натуральным числом
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
В данной публикации мы рассмотрим, каким образом десятичную дробь можно сложить с другой дробью (десятичной и обыкновенной) или целым натуральным числом. Также разберем примеры для лучшего понимания представленного материала.
- Правило сложения десятичных дробей
- Примеры
Правило сложения десятичных дробей
Сумма десятичных дробей находится путем их сложения столбиком. Порядок действий следующий:
1. Одноименные разряды пишем друг под другом: десятые под десятыми, сотые под сотыми, тысячные под тысячными и т.д.
Примечание: При необходимости (если количество цифр после запятой у суммируемых дробей разное), в конце более “короткой” дроби с меньшим количеством знаков после запятой добавляем нули, чтобы выровнять ее с более “длинной”. Согласно основному свойству десятичной дроби, это никоим образом не отразится на ее величине.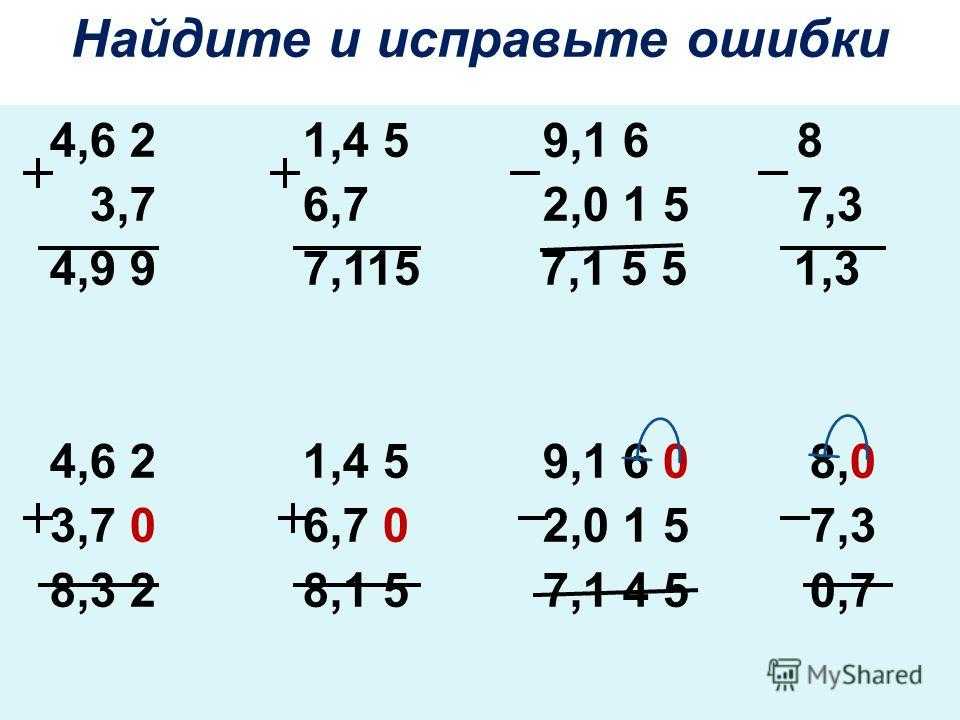
2. Десятичные разделители (запятые), также, должны находится строго друг под другом.
Примеры неправильной записи слагаемых:
Примеры правильной записи слагаемых:
3. Складываем дроби, как будто имеем дело с целыми натуральными числами. Т.е. на запятые внимания не обращаем.
4. В полученном результате ставим запятую строго там же, где она стояла в суммируемых дробях.
Сумма десятичной дроби и целого натурального числа
Если к десятичной дроби требуется прибавить целое натуральное число, то в конце последнего ставим запятую, после которой добавляем столько нулей, сколько цифр содержится в дробной части десятичной дроби. Затем вычисляем сумму слагаемых.
Сложение десятичной и обыкновенной дробей
Чтобы найти сумму десятичной и обыкновенной дробей, последнюю переводим в десятичную. После этого выполняем сложение.
Можно поступить наоборот – десятичную дробь преобразовать в обыкновенную. В этом случае уже складываем обыкновенные дроби.
Примеры
Давайте найдем сумму десятичных дробей, рассмотренных выше:
Примечание: если сумма десятых в дробной части результата больше 10, то единицу держим в уме и переносим ее в целую часть.
И, напоследок, вычислим сумму десятичной дроби и целого числа:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Как перевести десятичную дробь в обычную дробь
Для начала, рассмотрим пример. Пусть у нас есть десятичная дробь \(0,75\). Чтобы перевести ее в обыкновенную, запишем в числителе число после запятой (75), а в знаменателе запишем \(10^2 = 100\), так как в данном случае два знака после запятой. Поэтому обычная дробь будет выглядеть как \(\frac{75}{100}\). Затем дробь можно сократить, разделив числитель и знаменатель на их общий делитель — в данном случае это число 25. Получаем \(\frac{3}{4}\). Итак, десятичная дробь \(0,75\) равна обыкновенной дроби \(\frac{3}{4}\). Чтобы перевести любую десятичную дробь в обыкновенную, нужно записать число после запятой в числителе, а в знаменателе написать нужное количество нулей, зависящее от количества знаков после запятой.





























