Вынесение общего множителя в тригонометрических уравнениях
Еще один распространенный на ЕГЭ тип тригонометрических уравнений, в которых необходимо вынести общий множитель.
Пример 27
$$\sin(2x)-2\sin^2(x)=0;$$
В этом уравнении только одна тригонометрическая функция — \(\sin(x)\). Но под синусами стоят разные выражения. Поэтому избавимся от двойного угла под синусом при помощи формулы синуса двойного угла:
$$\sin(2x)=2\sin(x)*\cos(x);$$
Уравнение примет вид:
$$2\sin(x)*\cos(x)-2\sin^2(x)=0;$$
Замечаем общий множитель \(2*\sin(x)\), вынесем его за скобки:
$$2*\sin(x)*(\cos(x)-\sin(x))=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Уравнение разбивается на два:
Либо:
$$2\sin(x)=0;$$
$$\sin(x)=0;$$
$$x_{1}=0+2\pi*n=2\pi*n, \quad n \in Z;$$
$$x_{2}=\pi+2\pi*n, \quad n \in Z;$$
(Кстати, эти два решения можно объединить в одно: \(x=0+\pi*n=\pi*n, \quad n \in Z;\))
Либо второе уравнение:
$$\cos(x)-\sin(x)=0;$$
Это уравнение решается при помощи деления. Разделим левую и правую часть уравнения на \(\cos(x)\):
$$\frac{\cos(x)-\sin(x)}{\cos(x)}=\frac{0}{\cos(x)};$$
$$1-\frac{sin(x)}{\cos(x)}=0;$$
$$1-tg(x)=0;$$
$$tg(x)=1;$$
$$x=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$
Ответ:
$$x_{1}=\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$
Пример 28
$$2\cos(\frac{\pi}{2}-x)=tg(x);$$
Сразу замечаем формулу приведения под косинусом:
$$\cos(\frac{\pi}{2}-x)=\sin(x);$$
Подставляем в исходное уравнение
$$2\sin(x)=tg(x);$$
Распишем тангенс по определению:
$$tg(x)=\frac{\sin(x)}{\cos(x)};$$
$$2\sin(x)=\frac{\sin(x)}{\cos(x)};$$
$$2\sin(x)-\frac{\sin(x)}{\cos(x)}=0;$$
И здесь тоже будет общий множитель \(\sin(x)\):
$$\sin(x)*(2-\frac{1}{\cos(x)})=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
Первый множитель:
$$\sin(x)=0;$$
$$x_{1}=0+\pi*n=\pi*n, \quad n \in Z;$$
Второй множитель:
$$2-\frac{1}{\cos(x)}=0;$$
Приведем к общему знаменателю:
$$\frac{2\cos(x)}{\cos(x)}-\frac{1}{\cos(x)}=0;$$
$$\frac{2\cos(x)-1}{\cos(x)}=0;$$
Дробь равна нулю, когда числитель равен нулю – избавляемся от знаменателя:
$$2\cos(x)-1=0;$$
$$2\cos(x)=1;$$
$$\cos(x)=\frac{1}{2};$$
$$x_{2}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$x_{3}=-\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
Ответ:
$$x_{1}=\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$x_{3}=-\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
Метод группировки в тригонометрических уравнениях
Рассмотрим еще уравнение, которое было на ЕГЭ 2015 года на метод группировки. Тоже нужно обязательно это знать. Сам метод, если кто не знает, сводится, по сути, к вынесению общего множителя за скобки, только немного сложнее.
Пример 29
$$\sin(2x)+\sqrt{2}\sin(x)=2\cos(x)+\sqrt{2};$$
Избавляемся от двойного угла:
$$2*\sin(x)\cos(x)+\sqrt{2}\sin(x)=2\cos(x)+\sqrt{2};$$
И перенесем все в левую часть:
$$2*\sin(x)\cos(x)+\sqrt{2}\sin(x)-2\cos(x)-\sqrt{2}=0;$$
У нас 4 слагаемых, сгруппируем их попарно: 1-е со 2-м, а 3-е с 4-м, и вынесем в каждой паре общий множитель:
$$\sin(x)(2\cos(x)+\sqrt{2})-1(2\cos(x)+\sqrt{2})=0;$$
У 3-го и 4-го слагаемых я вынес за скобки \(-1\).
Теперь обратите внимание, что в скобках получились идентичные выражения, то есть эти скобки абсолютно одинаковые. Вынесем эту общую скобку за скобку!
$$(2\cos(x)+\sqrt{2})(\sin(x)-1)=0;$$
Вот мы и сгруппировали, теперь приравниваем каждый множитель к нулю:
Первый множитель:
$$2\cos(x)+\sqrt{2}=0;$$
$$\cos(x)=\frac{-\sqrt{2}}{2};$$
$$x_{1}=\frac{3\pi}{4}+2\pi*n, \quad n \in Z;$$
$$x_{2}=-\frac{3\pi}{4}+2\pi*n, \quad n \in Z;$$
Второй множитель:
$$\sin(x)-1=0;$$
$$\sin(x)=1;$$
$$x_{3}=\frac{\pi}{2}+2\pi*n, \quad n \in Z;$$
Получение функции arctg .
Есть функция y = tg x
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arctg x
не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает все значения лишь 1 раз — . На таком отрезке y = tg x
только возрастает монотонно и принимает все значения лишь 1 раз, то есть, на интервале есть обратная y = arctg x
, график ее симметричен графику y = tg x
на отрезке относительно прямой y = x
.
Арктангенс и арккотангенс числа а
Равенство
tg φ
= а
(1)
определяет угол φ
неоднозначно. В самом деле, если φ
0 есть угол, удовлетворяющий равенству (1), то в силу периодичности тангенса этому равенству будут удовлетворять и углы
φ
0 + nπ
,
где n
пробегает все целые числа (n = 0, ±1, ±2, ±3, . . .). Такой неоднозначности можно избежать, если дополнительно потребовать, чтобы угол φ
находился в пределах — — π /
2
φ
π /
2
. Действительно, в интервале
— π /
2
x
π /
2
функция у = tg x
монотонно возрастает от — ∞ до + ∞.
Следовательно, в этом интервале тангенсоида обязательно пересечется с прямой у =
а
и притом лишь в одной точке. Абсциссу этой точки принято называть арктангенсом числа а и обозначать arctg
a
.
Арктангенс а
есть угол, заключенный в интервале от — π /
2 до + π /
2 (или от -90° до +90°), тангенс которого равен а
.
Примеры.
1). arctg 1 = π /
4
или arctg 1 = 45°
. Действительно, угол в π /
4
радианов попадает в интервал (- π /
2
, π /
2
) и тангенс его равен 1.
2) arctg (- 1 / \/ 3
) = — π /
6 ,
или arctg (- 1 / \/ 3
) = -30°
. Действительно, угол в -30° попадает в интервал (-90°, 90°), тангенс его равен — 1 / \/ 3
Заметим, что из равенства
tg π
= 0
нельзя заключить, что arctg 0 = π
. Ведь угол в π
радианoв не попадает в интервал (- π /
2
, π /
2
) и потому он не может быть арктангенсом нуля. Читатель, по-видимому, уже догадался, что arctg 0 = 0.
Равенство
ctg φ
= а
, (2)
так же как и равенство (1), определяет угол φ
неоднозначно. Чтобы избавиться от этой неоднозначности, нужно на искомый угол наложить дополнительные ограничения. В качестве таких ограничений мы выберем условие
0 π
.
Если аргумент х
непрерывно возрастает в интервале (0, π
), то функция у = ctg x
будет монотонно убывать от + ∞ до — ∞. Поэтому в рассматриваемом интервале котангенсоида обязательно пересечет прямую у =
а
и притом лишь в одной точке.
Абсциссу этой точки принято называть арккотангенсом числа а
и обозначать arcctg
a
.
Арккотангенс а
есть угол, заключенный в интервале от 0 до π
(или от 0° до 180°), котангенс которого равен а
.
Примеры
.
1) arcctg 0 = π /
2
, или arcctg 0 = 90°
. Действительно, угол в π /
2
радианов попадает в интервал» (0, π
) и котангенс его равен 0.
2) arcctg (- 1 / \/ 3
) = 2π /
3
, или arcctg (- 1 / \/ 3
) =120°
. Действительно, угол в 120° попадает в интервал (0°,180°) и котангенс его равен — 1 / \/ 3
.
Заметим, что из равенства
ctg (- 45°) = -1
нельзя заключить, что arcctg (-1) = — 45°. Ведь угол в — 45° не попадает в интервал (0°, 180°) и потому он не может быть арккотангенсом числа -1. Очевидно, что
arcctg (—
1) = 135°.
Упражнения
I. Вычислить
:
1). arctg0 + arctg 1
/ \/
3
+ arctg \/
3
+ arctg 1.
2). arcctg0 + arcctg 1
/ \/
3
+ arcctg \/
3
+ arcctg 1.
3). arcctg 0 + arcctg (- 1) -arcctg (- 1
/ \/
3
) + arcctg(- \/
3
).
4). arctg (- 1) + arctg (- \/
3
) — arctg (- 1
/ \/
3
) — arctg 0.
II. Какие значения могут принимать величины а
и b
, если b
= arctg a
?
III. Какие значения могут принимать величины а
и b
, если b
= arcctg а
?
IV. В. каких четвертях оканчиваются углы:
а) arctg 5; в) arcctg 3; д) π /
2
— arcctg (- 4);
б) arctg (- 7); г) arcctg (- 2); е) 3π /
2
+ arctg 1 /
2
?
V. Могут ли выражения arctg
а
и arcctg
а
принимать значения: а) одного знака; б) разных знаков?
VI. Найти синусы, косинусы, тангенсы и котангенсы следующих углов:
а) arctg 5 /
12
; в) arcctg (- 5 /
12
);
б) arctg (-0,75); г) arcctg (0,75).
VII. Доказать тождества
:
1). arctg (-х
) = — arctg x
.
2). arcctg (-х
) = π
— arcctg x
.
VIII. Вычислить
:
1). arcctg (ctg 2).
Основные формулы
Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.
В первую группу входят формулы, справедливые на всей области определения обратных функций:sin(arcsin
x)
= x
cos(arccos
x)
= x
tg(arctg
x)
= x
(-∞ ctg(arcctg
x)
= x
(-∞
Во вторую группу входят формулы, справедливые только на множестве значений обратных функций. arcsin(sin
x)
= x
при arccos(cos
x)
= x
при arctg(tg
x)
= x
при arcctg(ctg
x)
= x
при
Если переменная x
не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n
— целое): sin
x = sin(-
x-π)
;
sin
x = sin(π-x)
;
sin
x = sin(x+2
πn)
;
cos
x = cos(-x)
;
cos
x = cos(2
π-x)
;
cos
x = cos(x+2
πn)
;
tg
x = tg(x+πn)
;
ctg
x = ctg(x+πn)
Например, если известно, что тоarcsin(sin
x)
=
arcsin(sin( π — x ))
= π — x .
Легко убедиться, что при π — x
попадает в нужный интервал. Для этого умножим на -1
: и прибавим π
:
или Все правильно.
Формулы
Формулы суммы и разности
при или
при 0,\,y>0 \;» style=»width:114px;height:18px;vertical-align:-10px;background-position:-638px -553px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
при и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
при или
при 0,\,y и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
при 0 \;» style=»width:108px;height:18px;vertical-align:-10px;background-position:-0px -571px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
Главные значения: arcsin, arccos, arctg и arctg
Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \ градусов. Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.
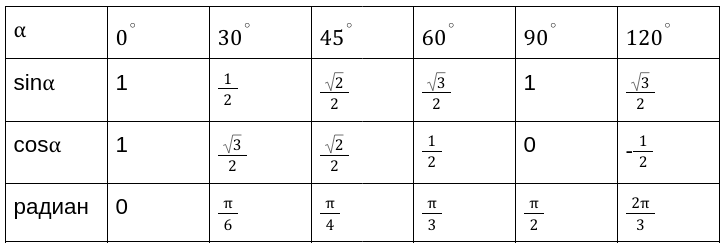
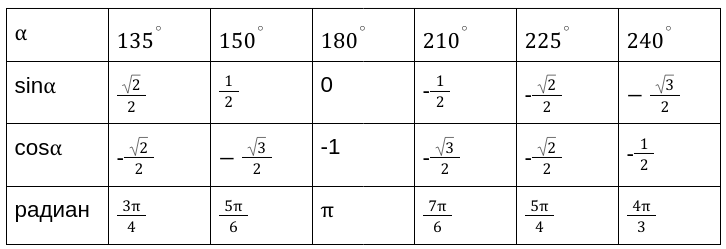Продолжение таблицы 1
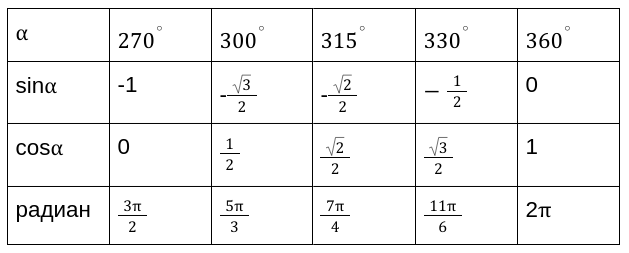
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.
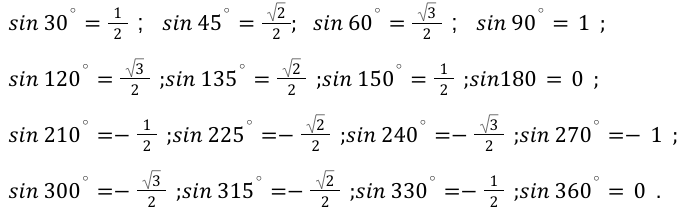
Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.
Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.
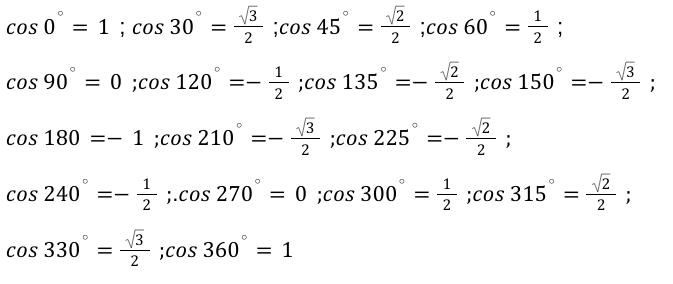
Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.
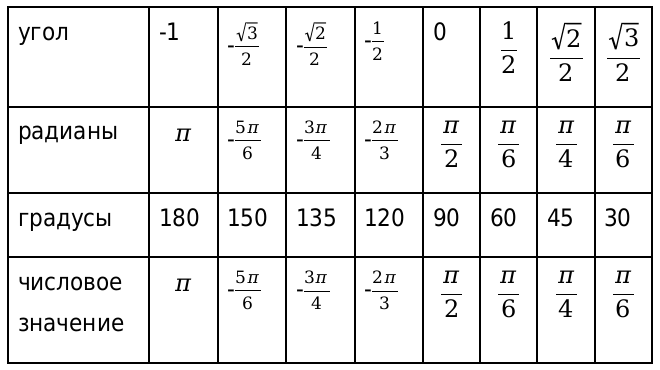
И напоследок остается вычислить значения арктангенса и арккотангенса.
Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:
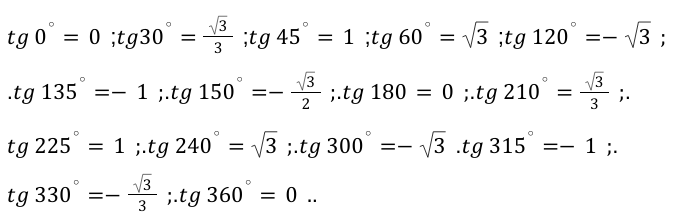
\ — данные угловые значения, не определяются, согласно основным законам геометрии и математики.
\- для перечисленных угловых значений по законам математики и всех технических наук в целом, значения не определяются
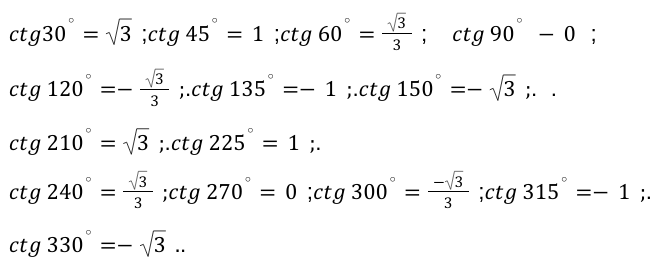
Далее все данные запишем в виде табличной формы.
Первая таблица для арктангенса
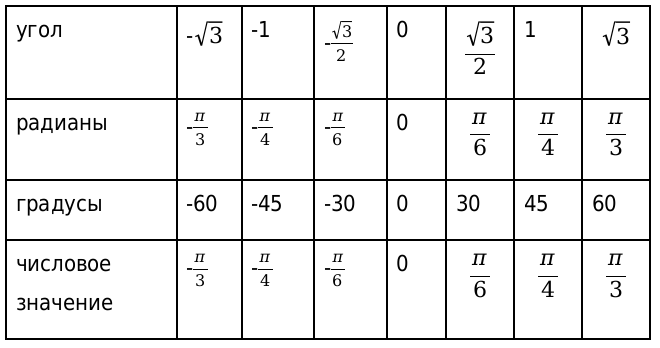
Вторая таблица для арккотангенса
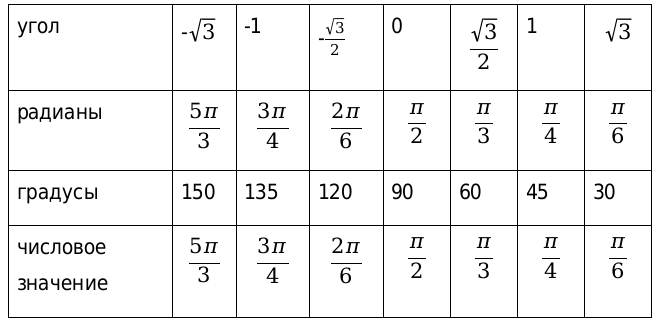
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
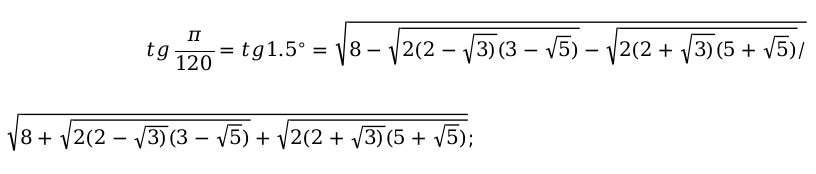
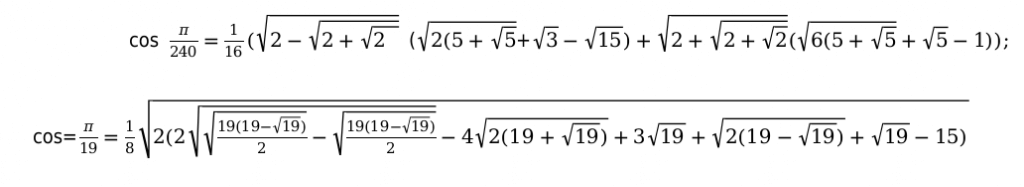
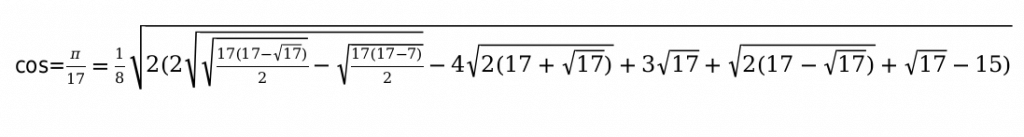
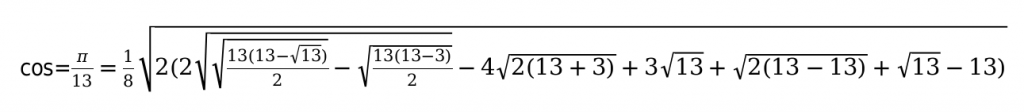
Основные способы, которые помогут заполнить таблицу функций тригонометрии.
Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции
Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec)
На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения.
Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.
В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Мы показали, что представляет таблица, какие данные и значения отображает. Полную версию таблицы, можно найти в сборнике. Который издается каждый год. Для определения неизвестных нужно использовать следующие уже известные нам формулы:
\
Пример решения:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102
\
Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение. Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.
Арксинус (y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
| Свойства функции | Функции y=arcsin х |
| E(f) | \ |
| D(f) | \ |
| наличие четности | Нечётная, т.к. arcsin(-x)= — arcsin x |
| характер графика направление | возрастание |
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y).
| Свойства | Функции y=arccos х |
| E(f) | \ |
| D(f) | \ |
| Чётности | Данное свойство ей не характерно. Иными словами отсутствует. |
| Монотонность | Убывающая |
Арктангенс ( y = arctg x ) – характеризуется, как обратное значение функции относительно тангенса.
Следовательно арккотангенс имеет такие свойства по отношению к тангенсу.
| Свойства | y=arctg х | y=arcctg х |
| E(f) | R | R |
| D(f) | \ | \ |
| Характер функции | Нечётная | Нечётная |
| Периоды | Возрастающая | Убывающая |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
График функции \(y = arccosx\)
Функция y=\arccos x не прерывается и ограничивается на протяжении всей своей области определения. Данная функция строго убывает и не является отрицательной. Характеристики понятия функции arccos, которые используют при ее нахождении:
- \(\cos(\arccos x)=x, когда -1\leqslant x\leqslant 1 \) (от минус единицы до плюс единицы);
- \(\arccos(\cos y)=y, если 0\leqslant y\leqslant \pi ;\)
- \(D(\arccos x)=\) является областью определения;
- \(E(\arccos x)=\) является областью множества значений.
Функцию \(y=\arccos x\) можно изобразить графически. В результате нужный график принимает следующий вид:
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
a r c sin α = a r c cos 1 — α 2 , 0 ≤ α ≤ 1 — a r c cos 1 — a 2 , — 1 ≤ α 0 a r c sin α = a r c t g α 1 — α 2 , — 1 α 1 a r c sin α = a r c c t g 1 — α 2 α , 0 α ≤ 1 a r c c t g 1 — α 2 α — π , — 1 ≤ α ≤ 0
А так мы выразим арккосинус через остальные обратные функции:
a r c cos α = a r c sin 1 — α 2 , 0 ≤ α ≤ 1 π — arcsin 1 — α 2 , — 1 ≤ α 0 a r c cos α = a r c t g 1 — α 2 α , 0 α ≤ 1 π + arctg 1 — α 2 α , — 1 α 0 arccosα = arcctg α 1 — α 2 , — 1 α 1
Формула выражения арктангенса:
a r c t g α = a r c sin α 1 + α 2 , — ∞ α + ∞ a r c t g α = a r c cos 1 1 + α 2 , α ≥ 0 — a r c cos 1 1 + α 2 , α 0 a r c t g α = a r c c t g 1 α , α ≠ 0
Последняя часть – выражение арккотангенса через другие обратные функции:
a r c c t g α = a r c sin 1 1 + α 2 , α ≥ 0 π — a r c sin 1 1 + α 2 , α 0 a r c c t g α = a r c cos α 1 + α 2 , — ∞ α + ∞ a r c c t g α = a r c t g 1 α , α ≠ 0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём a r c sin α = a r c t g α 1 — α 2 , — 1 α 1 и постараемся вывести доказательство.
Мы знаем, что a r c t g α 1 — α 2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin ( a r c t g α 1 — α 2 ) = α 1 — α 2 1 + ( α 1 — α 2 ) 2 = α 1 — α 2 1 + α 2 1 — α 2 = α 1 — α 2 1 + α 2 1 — α 2 = α 1 — α 2 1 1 — α 2 = α
Получается, что a r c t g α 1 — α 2 при условии 1 a 1 – это и есть арксинус числа a .
Вывод: a r c sin a = a r c t g a 1 — a 2 , — 1 a 1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Условие Вычислить синус арккотангенса минус корня из 3 .
Решение
Нам понадобится формула выражения арккотангенса через арксинус: a r c c t g α = a r c sin 1 1 + a 2 , α ≥ 0 π — arcsin 1 1 + a 2 , α 0 Подставим в нее α = — 3 и получим ответ – 1 2 . Непосредственное вычисление дало бы нам те же результаты: sin ( a r c c t g ( — 3 ) ) = sin 5 π 6 = 1 2 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sin α = 1 1 + c t g 2 α , 0 α π
В итоге у нас бы вышло: sin ( a r c c t g ( — 3 ) ) = 1 1 + c t g 2 ( a r c c t g ( — 3 ) ) = 1 1 + ( — 3 ) 2 = 1 2
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin ( a r c c t g α ) = 1 1 + α 2 sin ( a r c c t g ( — 3 ) ) = 1 1 + ( — 3 ) 2 = 1 2
Замена переменной в тригонометрических уравнениях
Замена выражения под тригонометрической функцией
Мы научились решать простейшие уравнения. И на этом строится решение всех остальных тригонометрических уравнений. Они все так или иначе сводятся к решению простейших. И один из способов – это введение замены переменной.
Вы должны были с этим регулярно сталкиваться в младших классах при решении, например, биквадратных уравнений. Все дальнейшие рассуждения предполагают, что вы знаете, что такое замена переменной. Итак, разберем пример:
Пример 18
$$\sin(2x)=\frac{\sqrt{3}}{2};$$
Обратите внимание, что теперь у нас под синусом стоит не просто \(x\), а целое выражение. Давайте избавимся от него, убрав \(2x\) в замену: пусть \(t=2x\)
Теперь наше уравнение превратилось в простейшее тригонометрическое. Решаем его относительно переменной \(t\) (вы можете решать при помощи единичной окружности или по готовым формулам, как вам удобнее. Я же буду просто выписывать ответ):
$$t_{1}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$t_{2}=\frac{2\pi}{3}+2\pi*n, \quad n \in Z;$$
На этом решение не заканчивается. Мы нашли значения \(t\), а нам надо найти \(x\). Делаем обратную замену, вспоминая, что \(t=2x\):
$$2x_{1}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$2x_{2}=\frac{2\pi}{3}+2\pi*n, \quad n \in Z;$$
И просто выражаем из получившихся выражений \(x\), для этого разделим левую и правую часть равенства на \(2\):
$$\frac{2x_{1}}{2}=\frac{\frac{\pi}{3}+2\pi*n}{2}, \quad n \in Z;$$
$$\frac{2x_{2}}{2}=\frac{\frac{2\pi}{3}+2\pi*n}{2}, \quad n \in Z;$$
$$x_{1}=\frac{1}{2}*\frac{\pi}{3}+\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{1}{2}*\frac{2\pi}{3}+\pi*n, \quad n \in Z;$$
Обратите внимание, что период тоже не забываем поделить на \(2\). Ответ:
$$x_{1}=\frac{\pi}{6}+\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{3}+\pi*n, \quad n \in Z.$$
Ответ:
$$x_{1}=\frac{\pi}{6}+\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{3}+\pi*n, \quad n \in Z.$$
Аналогичным образом можно решать тригонометрические уравнения с более сложным подтригонометрическим выражением:
Пример 19
$$tg(\frac{2x+\pi}{3})=1;$$
Под тангенсом тут стоит целая дробь, зависящая от \(x\). Засунем всю эту дробь в замену:
$$t=\frac{2x+\pi}{3};$$
Уравнение примет вид:
$$tg(t)=1;$$
Решением этого простейшего уравнения будет:
$$t=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$
Делаем обратную замену, вместо \(t\) подставляем \(\frac{2x+\pi}{3}\):
$$\frac{2x+\pi}{3}=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$
И выражаем отсюда \(x\). Домножим равенство на \(3\):
$$2x+\pi=3*(\frac{\pi}{4}+\pi*n), \quad n \in Z;$$
$$2x+\pi=\frac{3\pi}{4}+3\pi*n, \quad n \in Z;$$
Перенесем \(\pi\) направо:
$$2x=-\pi+\frac{3\pi}{4}+3\pi*n, \quad n \in Z;$$
Приведем подобные слагаемые:
$$2x=-\frac{\pi}{4}+3\pi*n, \quad n \in Z;$$
И разделим на \(2\):
$$x=-\frac{\pi}{8}+\frac{3}{2}*\pi*n, \quad n \in Z;$$
Ответ:
$$x=-\frac{\pi}{8}+\frac{3}{2}*\pi*n, \quad n \in Z;$$
Замена всей тригонометрической функции
Что делать с подтригонометрическим выражением, мы разобрались. Теперь решим пример на замену, при помощи которой тригонометрическое уравнение сводится к квадратному.
Пример 20
$$2*\sin^2(x)+\sin(x)-1=0;$$
Обращаем внимание на одинаковое выражение \(\sin(x)\). Сделаем замену:
$$t=\sin(x);$$
$$2t^2+t-1=0;$$
Получили обыкновенное квадратное уравнение, которое решается через дискриминант:
$$D=1-4*2*(-1)=9;$$
$$t_{1}=\frac{-1+3}{4}=\frac{1}{2};$$
$$t_{2}=\frac{-1-3}{4}=-1;$$
Делаем обратную замену и получаем два простейших тригонометрических уравнения
Первое:
$$\sin(x)=\frac{1}{2};$$
$$x_{1}=\frac{\pi}{6}+2\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{5\pi}{6}+2\pi*n, \quad n \in Z;$$
Второе:
$$\sin(x)=-1;$$
$$x_{3}=\frac{3\pi}{2}+2\pi*n, \quad n \in Z;$$
Записываем ответ из трех наборов решений.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Поскольку то умножив на -1
, имеем: или Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Аналогично для остальных функций.arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x