Свойства синуса
Ниже в табличной форме представлены основные свойства синуса с формулами:
| Свойство | Формула |
| Симметрия | грех (-α) = -sinα «порядок данных=»sin (-α) = -sin α»>sin (-α) = -sinα |
| Симметрия | sin (90°- α) = cos α» data-order=»sin (90°- α) = cos α»> sin (90°- α) = cos α |
| Пифагорейское тригонометрическое тождество | sin2 α + cos2 α = 1″ порядок данных=»sin2 α + cos2 α = 1″>sin2α + cos2α = 1 |
| sin α = cos α tg α» data-order=»sin α = cos α tg α»> sin α = cos α tg α | |
| грех α = 1 / csc α» порядок данных=»sin α = 1 / csc α»> sin α = 1 / csc α | |
| Синус двойного угла | грех 2α = 2 грех α потому что α» порядок данных=»sin 2α = 2 sin α cos α»> sin 2α = 2 sin α cos α |
| Синус суммы углов | грех (α + β) = грех α, потому что β + потому что α, грех β» data-order=»sin (α+β) = sin α cos β + cos α sin β»> sin (α + β) = sin α cos β + cos α sin β |
| Синус угловой разности | грех (α-β) = грех α, потому что β — потому что α, грех β» data-order=»sin (α-β) = sin α cos β — cos α sin β»>sin(α-β) = sin α cos β — cos α sin β |
| Сумма синусов | |
| Разница синусов | |
| Произведение синуса | |
| Произведение синуса и косинуса | |
| Закон синуса | a / sin α = b / sin β = c / sin γ» data-order=»a / sin α = b / sin β = c / sin γ»>a/sin α = b/sin β = c/sin γ |
| Синусоидальная производная | грех х = потому что х» порядок данных=»sin’ x = cos x»> грех х = потому что х |
| Синусоидальный интеграл | ∫ sin x dx = -cos x + C» data-order=»∫ sin x dx = -cos x + C»>∫ sin x dx = -cos x + C |
| Формула Эйлера | sin x = (eix — e-ix) / 2i» data-order=»sin x = (eix — e-ix) / 2i»> sin x = (eix — e-ix) / 2i |
Вычисление тригонометрических функций числа
В данном пункте рассмотрим случай, когда определение рассматриваемых нами функций тригонометрии, происходит из числового значения, а не угла. Таких подходов два:
- Sin, cos, tg, ctg числа n, является число которое равно sin, сos, tg, ctg n радиан. Где Радиа́н это угол, который соответствует дуге, которая в свою очередь равна длине, её радиуса. Пример: sin числа2k=sin угла2k радиан. Используя формулы можно получить таблицу часто встречаемых углов, которая поможет быстро перевести значения из градусов в радианы и в противоположную сторону.
- На прямоугольной системе координат, в единичной окружности, ставится точка, которой соответствует любое действительное значение числа d. тригонометрические функции можно определить, узнав координаты этой точки.
- Считая начальной точкой А с координатами (1,0). Поэтому для того чтобы найти взаимодействие между точкой на окружности и числом, нужно найти отрицательное и положительное значение числа d, положительным будет значение при движении точки А(1,0) в противоположную сторону движения часовой стрелки и её движение будет равным open t \ t, а отрицательным движение по часовой стрелке.
В связи с этим выделяют следующие функции:
- (sin f = y) Синус числа f- определяется ординатой точки единичной окружности, которая равна числу f;
- (cos f = x) Косинус числа f — абсцисса окружности, которая соответствующая числу f;
- (tg f = y\x=sin f\cos f) тангенс f определяется делением ординаты на абсциссу точки, равной числу f.
Что такое таблицы тригонометрических функций
Определение
Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе.
Для определения неизвестных элементов треугольника (сторон или углов), необходимо использовать известные элементы и правила зависимости между ними. Подобные зависимости называют также тригонометрическими функциями. Таким образом, зная значения некоторого угла или стороны, пользуясь тригонометрическими функциями можно найти неизвестные углы и стороны треугольника. Именно поэтому, без знаний тригонометрии решать геометрические задачи не представляется возможным.
Основные тригонометрические функции:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
- Синус — отношение противолежащего катета к гипотенузе.
- Косинус — отношение прилежащего катета к гипотенузе.
- Тангенс — отношение противолежащего катета к прилежащему. Также равен частному от деления синуса определенного угла на его косинус.
- Котангенс — отношение прилежащего катета к противолежащему. Также равен частному от деления косинуса определенного угла на его синус.
Примечание
Синус и косинус являются прямыми тригонометрическими функциями, тангенс и котангенс — производными. Существуют и другие тригонометрические функции, например — арктангенс. Арктангенс относится к так называемым обратным тригонометрическим функциям, и является функцией, обратной тангенсу. Это означает, что если тангенс некоторого угла у градусов (радиан) равен х, значит арктангенс x равняется y градусов (радиан).
Вычисленные тригонометрические функции (синус, косинус и тангенс) представляют в виде специальных таблиц, которые можно использовать при решении задач — это и есть таблицы тригонометрических функций. В них приведены значения тригонометрических функций углов от 0° до 360°.
Для прямоугольных треугольников в диапазоне углов от 30° до 90° тригонометрические функции равняются следующим значениям:
sin 30° = 1/2, cos 30° = √3/2, tg 30° = √3/3, ctg 30° = √3
sin 45° = √2/2, cos 45° = √2/2, tg 45°= 1, ctg 45° = 1
sin 60° = √3/2, cos 60° = 1/2, tg 60° =√3 , ctg 60° = √3/3
Как выглядит для значений, синуса, косинуса, тангенса и котангенса
Таблица тригонометрических функций выглядит следующим образом:
Значение аргумента α задано в верхней строке задано в градусах (от 0° до 90°), во второй строке — в радианах (0, π/6, π/4, π/3, π/2 радиан). Иногда в таблице присутствуют значения только в радианах. Для перевода в градусы необходимо подставить число π = 180°, например, π/6 = 180/6 = 30°.
Обозначение «не определен» в таблице (тангенс 90° и котангенс 0°) означает, что функция является неопределенной.
Пример
Алгоритм решения задач с помощью данной таблицы крайне прост. К примеру, нам необходимо найти значение косинуса 30°. Для этого найдем ячейку пересечения строки косинуса и столбца значений для 30°. В данной ячейке находится искомое значение.
Стандартные углы
Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
- Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
\
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:
\
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
\
И с углом 30°:
\
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:
\
Итак, мы знаем синус
Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$
Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
И наоборот:
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
Таблица функций тригонометрии
Эта таблица представляет из себя уже посчитанные значения sin, cos, tg, ctg углов от 0до 360 градусов. Такая таблица заменит специальный калькулятор если нужны значения, нужно просто найти нужный угол в таблице.
Области применения тригонометрии
Приведём для примера несколько областей в которых применяются функций:
- В астрономии. Во-первых, как отмечалось выше область астрономии стала первой, где стали применять тригонометрические функции. Именно по этой причине довольно долго этот раздел науки относили к астрономии. Одним из крупных открытий в этой науке при помощи тригонометрических основ стала возможность вычисления наступления темноты, а также составление первых звёздных карт.
- В физике. Мир, который нас окружает построен на колебательных процессах, это такие явления и процессы, которые повторяются через определённый цикл;
- В окружающей нас природе. Например, отражение лучей солнца от различных поверхностей;
- В медицине. К примеру, существует такое понятие как формула сердца;
- В биологии. Биологические ритмы, модель которых строят при помощи тригонометрии;
- В музыке, звуковые ритмы, построение моделей.
- Важную роль тригонометрия играет и для морского флота и авиации;
- В изучении сейсмической активности.
Как мы видим тригонометрия очень важная наука, которая пронизывает практически все сферы нашей жизни.
Определения функций и их связь
Вернемся к единичной окружности в прямоугольной системе координат, где центр окружности и системы координат совпадает. Точку А(1,0) повернём на 90°, и из полученной точки А1 проведём перпендикуляр к абсциссе. В результате получится прямоугольный треугольник, где угол А1 ОН это угол поворота а. длины катета ОН и абсциссы точки А1 также равны. А катет, который находится напротив угла равен ординате точки А1, а длина гипотенузу это единица.
Получается исходя из определения, синус угла а, это отношение катета напротив к гипотенузе.
sin α = A 1 H\ O A 1 = y \1 = y
sin α=A1H\OA1=y\1=y
Из чего следует, что определение sin острого угла, одинаково определению синуса угла поворота а, если а лежит в пределе 0-90°. Точно так же и с вычислением косинуса, тангенса и котангенса.
Угол поворота.
Как уже говорилось выше определения, которые мы рассмотрели относятся к острым углам треугольника. Но существует и понятие угол поворота, в котором исчисляемый угол не будет равен значению от 0 градусов до 90. При этом угол поворота может быть любым числом, от +бесконечности и до — бесконечности.
В данной связи можно выдвинуть определение синуса, косинуса, тангенса и котангенса угла любой величины. Для этого представим окружность в системе координат с двумя взаимно перпендикулярными осями.
Заданная точка А, имеющая координатные значения 1,0, делает поворот вокруг центра оси на угол α, переходя в точку А1. рассматривая определение через координаты А1(х,у).
Sin угла поворота α, это ордината точки А1(х,у), то есть sinα=у
Косинус α — абсцисса точки А1 (cosα=х)
Tg данного угла — ‘это деление (отношение) ординаты А1 к абсциссе. tgα=у\х
Котангенс поворотного угла α — отношение её абсциссы к ординате, ctgα=х\у
Заметим, что синус и косинус можно выделить для любого угла, а вот тангенс и котангенс нет. И это абсолютно логично, так как при переходе точки в значение ноля для абсциссы, тангенс посчитать невозможно, так как невозможно деление на 0. Тоже самое со значением ординаты равным нулю, котангенс не исчисляется.
Sin и cos можно вычислить для любых углов α. тогда как tg всех кроме α = 90°+180°* k , k ∈ Z ( α = π 2 + π * k , k ∈ Z ) α=90°+180°*k, k∈Z (α=π2+π*k, k∈Z)
Котангенс так же можно вычислить не для всех углов, например для α = 180 ° * k , k ∈ Z ( α = π * k , k ∈ Z , это сделать нельзя.
Отметим, что на практике при решении примеров словосочетание угол поворота опускается из речевого оборота.
Для удобства существуют таблицы значений часто используемых углов, которые вычисляются в тригонометрических функциях, к примеру, для первой четверти круга:
| 0° | 30° | 45° | 60° | 90° | |
| sin | 1 2 | √2 2 | √3 2 | 1 | |
| cos | 1 | √3 2 | √2 2 | 1 2 | |
| tg | 1 √3 | 1 | √3 | – | |
| ctg | – | √3 | 1 | 1 √3 |
Здесь можно посмотреть таблицу синусов, косинусов и других функций.
Правило встречается в следующих упражнениях:
7 класс
Задание 591, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 642, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 704, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1024, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1037, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1117, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1238, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1307, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Что такое таблица синусов π и таблица Брадиса
В таблице синусов значение угла α дается в:
в виде числа, выраженного через квадратный корень.
Это таблица не только для синусов, но и для других тригонометрических знаков. Но в данном случае, мы приведем таблицу только для синусов.
| Значение угла α (градусов) |
Значение угла α в радианах (через число пи) |
sin (синус) |
|---|---|---|
| 15 | π/12 | (√3 — 1)/2√2 |
| 30 | π/6 | 1/2 |
| 45 | π/4 | √2/2 |
| 60 | π/3 | √3/2 |
| 75 | 5π/12 | (√3 + 1)/2√2 |
| 90 | π/2 | 1 |
| 105 | 7π/12 | (√3 + 1)/2√2 |
| 120 | 2π/3 | √3/2 |
| 135 | 3π/4 | √2/2 |
| 150 | 5π/6 | 1/2 |
| 180 | π | |
| 210 | 7π/6 | -1/2 |
| 240 | 4π/3 | -√3/2 |
| 270 | 3π/2 | -1 |
| 360 | 2π |
Рассчитываем калькулятором значение π, данные можно посмотреть в таблице. Здесь включены значения синуса, которых нет в таблицах Брадиса, вычисления сделаны с точностью до 4 знака. Если нужно узнать, чему равен синус, это всегда можно посмотреть в таблице или рассчитать самому.
| Значение sin угла α в градусах | Значение sin угла α в радианах | Значение синуса угла α |
|---|---|---|
| Синус угла 0 градусов | ||
| Синус угла 15 градусов | π/12 | 0.2588 |
| Синус угла 30 градусов | π/6 | 0.5 |
| Синус угла 45 градусов | π/4 | 0.7071 |
| Синус угла 50 градусов | 5π/18 | 0.766 |
| Синус угла 60 градусов | π/3 | 0.866 |
| Синус угла 65 градусов | 13π/36 | 0.9063 |
| Синус угла 70 градусов | 7π/18 | 0.9397 |
| Синус угла 75 градусов | 5π/12 | 0.9659 |
| Синус угла 90 градусов | π/2 | 1 |
| Синус угла 105 градусов | 5π/12 | 0.9659 |
| Синус угла 120 градусов | 2π/3 | 0.866 |
| Синус угла 135 градусов | 3π/4 | 0.7071 |
| Синус угла 140 градусов | 7π/9 | 0.6428 |
| Синус угла 150 градусов | 5π/6 | 0.5 |
| Синус угла 180 градусов | π | |
| Синус угла 270 градусов | 3π/2 | -1 |
| Синус угла 360 градусов | 2π |
Таблица синусов и её применение
Для начала нужно напомнить, что означает такое понятие, как синус угла.
Это справедливо в случае, если треугольник прямоугольный.
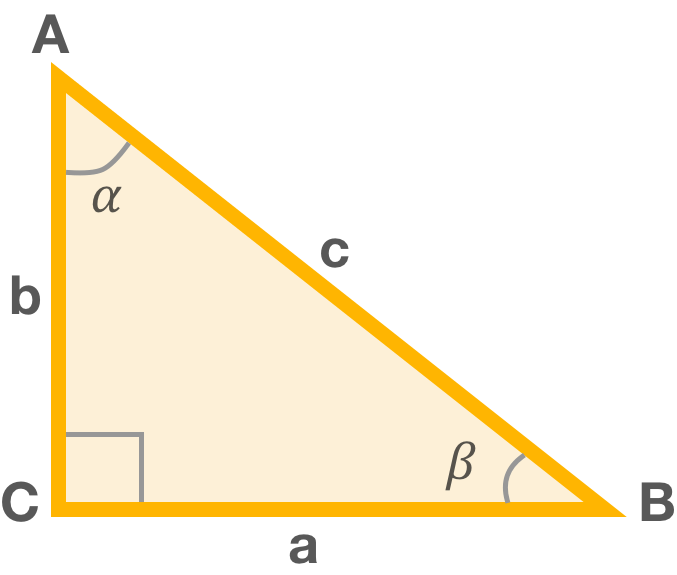
Стандартный прямоугольный треугольник: стороны a (BC) и b (AC) – катеты, сторона с (AB) – гипотенуза
Если взять тригонометрическую таблицу Брадиса для решения задач, можно убедиться на личном примере, что таблица синусов является одной из наиболее применяемых таблиц. Эта статья посвящена тому, как научиться находить значение синуса (sin) углов, от 0 до 90° и научиться это значение применять для решения задач. Кстати, её разработал и опубликовал в 1921 году педагог из Твери Владимир Модестович БРАДИС
Несмотря на то, что в 2021 году она отметит свой столетний юбилей, актуальность таблица Брадиса не утратила. В частности ее применяют архитекторы, проектанты, конструктора для проведения быстрых промежуточных расчетов.
Таблицы Брадиса разрешены к использованию в школах при сдаче ЕГЭ, в отличие от калькуляторов.
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, c — гипотенуза.
| Теорема косинусов звучит так: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α |
При доказательстве теоремы косинусов мы используем формулу длины отрезка в координатах. Рассмотрим эту формулу:
ВС2 = (х2 — х1)2 + (у2 — у1)2
В доказательстве теоремы косинусов ВС — сторона треугольника АВС, которую обозначают буквой а. Введем практическую систему координат и найдем координаты нужных нам точек. Точка B имеет координаты (c; 0).
Координаты точки C равны (b cos α; b sin α) для α ∈ (0°; 180°).
cos2α + sin2α = 1 — основное тригонометрическое тождество.
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
КЭД
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на математические онлайн-курсы для детей и подростков.
Используя закон косинусов, можно найти косинус угла треугольника:
- При b2 + c2 — a2 > 0 угол α будет острым.
- При b2 + c2 — a2 = 0 угол α будет прямым.
- При b2 + c2 — a2 < 0 угол α будет тупым.
Помните: когда угол α прямой, теорема косинусов становится теоремой Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Получим треугольник ABC, в котором высота CD опущена от вершины C к стороне AB. Это означает:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b × cos α)2
- h2 = a2 — (c – b × cos α)2
Приравняем правильные части уравнений:
b2 — (b × cos α)2 = a2 — (c — b × cos α)2
или
a2 = b2 + c2 — 2bc × cosα
Если один из углов у основания тупой (высота упирается в продолжение основания), то это точно так же, как обсуждалось выше.
Определим стороны b и c:
- b2 = a2 + c2 — 2ac × cosβ;
- c2 = a2 + b2 — 2ab × cos γ.
Тангенс и котангенс через синус и косинус
Несколько вступлений:
- Синус угла — это ордината у.
- Косинус угла — это абсцисса x.
- Тангенс угла – это отношение ординаты к абсциссе.
- Котангенс угла – это отношение абсциссы к ординате.
Из всего этого множества красивых, но не очень понятных слов можно сделать вывод, что одно зависит от другого. Такое соединение помогает отдельно преобразовывать нужные величины.
- tga =
- ctga =
На основании определений:
- tga =
= - ctga =
=
Это позволяет сделать вывод, что тригонометрические тождества
даны углы sin и cos.
Отсюда следует, что тангенс угла есть отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых укладываются в диапазон.
Например, выражение
относится к любому углу α, не равному
+ π + z, где z — любое целое число. В противном случае знаменатель будет равен 0.
Выражение
выполняется для любого угла α, не равного π * z, где z — любое целое число.
Что такое синус, косинус, тангенс и котангенс?
Тригонометрия в какой-то степени относится и к алгебре, и к геометрии. В этом уроке мы обсудим геометрическую часть тригонометрии.
А именно, нам понадобится прямоугольный треугольник. Это такой треугольник, в котором один из углов 90 градусов. Стороны, образующие прямой угол, называются катеты, для удобства обозначим их какими-нибудь буквами, например, \(a\) и \(b\). А гипотенузой называют сторону треугольника, лежащую напротив прямого угла, пусть она у нас будет \(c\). И обозначим острые углы в треугольнике за \(\alpha\) и \(\beta\).
С обозначениями закончили, без них изучать тригонометрию будет проблематично.
Что такое синус и зачем он нужен?
Вульгарное объяснение: синус — это математическое поле, в которое вставляется любое число, а в ответ оно выдает числа от −1 до 1. Если эти числа выстроить на определенной оси, получится такая кривая:
Как читать эту кривую: Если вы поместите число, примерно равное 1,57, в поле «sin», поле выведет число, близкое к единице. Если вы нажмете цифру 2, выход будет примерно 0,909. Если вы нажмете около 3,14, он вернет около 0. Синус 4,712 даст около -0,999. И так далее: число может быть сколь угодно большим, а синус всегда будет возвращать какое-то дробное значение от -1 до 1.
Это число взято из тригонометрии — то есть из науки, которая занимается углами и сторонами треугольника. В частности, синус описывает отношение между сторонами прямоугольного треугольника: насколько один из катетов (короткая сторона треугольника) короче гипотенузы (длинной стороны треугольника). Но чаще всего нам известны не длины сторон, а угол между ними, поэтому значения углов всегда записываются в синусы.
Грубо говоря, вы говорите ящику: «Коробка, у меня здесь прямоугольный треугольник. Смотрю на острый угол, это 30º. Что ты мне хочешь сказать?» А коробка отвечает: «Если угол равен 30º, то короткая сторона треугольника вдвое короче длинной гипотенузы. Итак, жалость (30º) = ½».
Это число очень нужно там в математике и компьютерах. Например, без синуса невозможно соединить две точки прямой линией на плоскости. Люди делают это легко линейкой, а вот компьютеру нужно очень четко сообразить, куда ставить пиксель, а для этого нужен синус.
Кроме синуса есть еще три аналогичные функции — косинус, тангенс и котангенс. Они в основном одинаковы, но описывают отношения с другими сторонами.
Многие языки программирования имеют встроенную команду для нахождения синуса угла — sin(). Внутри этой функции подключена некоторая логика для нахождения этого числа.
Чаще всего, когда не требуется высокой точности, компьютер берет значения синуса из готовых таблиц — находит там нужный угол и возвращает значение, ничего не вычисляя. Это достаточно быстро и точно для повседневного использования. Вы, наверное, использовали его в школе, когда считали пазухи в таблице Брадиса.
Таблица Брейди, по которой компьютер находит значения синуса с точностью до 4 знаков после запятой
Но когда требуется высокая точность вычислений (например, 20 знаков после запятой), синус и другие тригонометрические функции вычисляются каждый раз с нуля. Для этого используется множество различных алгоритмов, и самым простым из них является использование рядов Тейлора.
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0,2588190451sin(π/6) = sin(30°) = 0,5sin(π/4) = sin(45°) = 0,7071067812sin (π/3) = sin(60°) = 0,8660254038sin(5π/12) = sin(75°) = 0,9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105 °) = 0,9659258263sin(2π/3) = sin(120°) = 0,8660254038sin(3π/4) = sin(135°) = 0,7071067812sin(5π/6) = sin(150° 1)(2π5/1.) = sin(165°) = 0,2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0,2588190451sin(7π/6) = sin(210°) = -0,5 sin(5π/4) = sin(225°) = -0,7071067812sin(4π/3) = sin(240°) = -0,8660254038sin(17π/12) = sin(255°) = -0,9659258263sin(3π)) = sin(270°) = -1sin(19π/12) = sin(285°) = -0,9659258263sin(5π/3) = sin(300°) = -0,8660254038sin(7π/4) = sin(315°) = -0,7071067812sin(11π/6) = sin(330°) = -0,5sin(23π/12) = sin(345°) = — 0,2588190451
Функции аргумента угла и числа
Каждому значению угла а, существует своё значение sin, сos, данного угла, которое ему соответствует. А также углам α, кроме от α = 90 ° + 180 ° * k , k ∈ Z ( α = π 2 + π * k , k ∈ Z ) будет соответствовать определенное значение тангенса. Так же котангенс α, кроме α = 180 ° * k , k ∈ Z ( α = π * k , k ∈ Z ).
Из чего следует что синус а, косинус а, тангенс а, котангенс а — это и есть функции углового аргумента.
Точно также определяются функции числового аргумента. Выбранное любое действительное число, имеет своё соответственное значение функций тригонометрии, все кроме перечисленных исключений.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь


















![Тригонометрические выражения и тригонометрические формулы [wiki.eduvdom.com]](http://rwvt.ru/wp-content/uploads/5/f/c/5fcb02d0a4993d09bfc26d4d12d7d4cb.jpeg)









