Матрица: что это такое простыми словами

Ступенчатая матрица

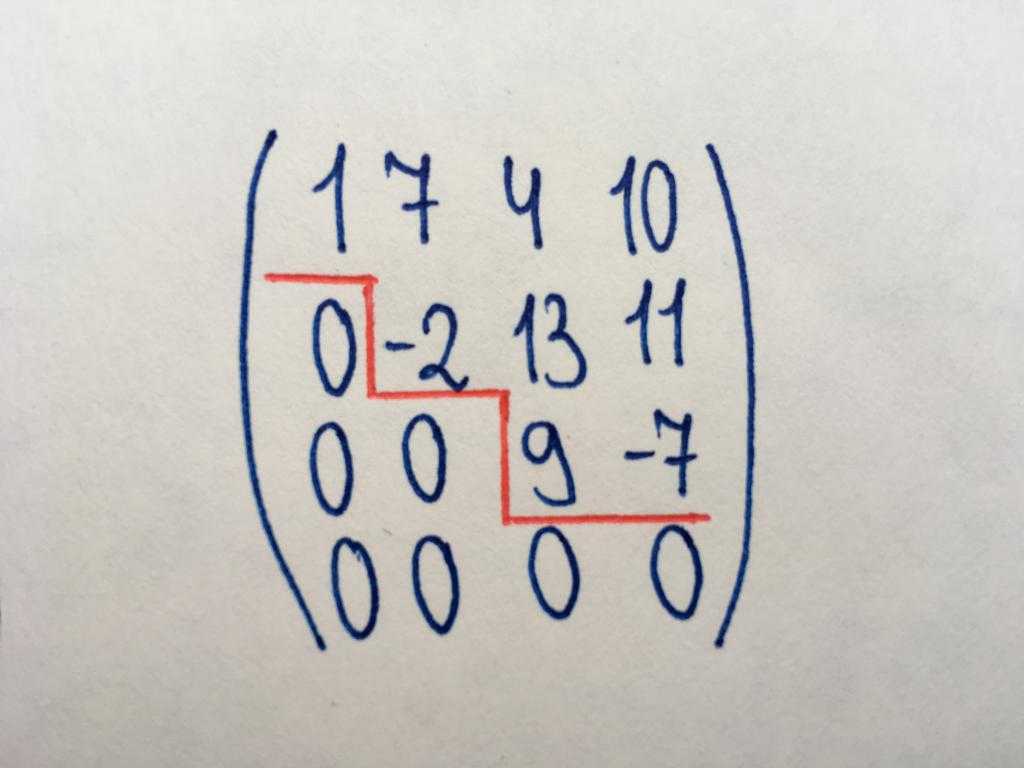
Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные «ступени» из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.

Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.

Какой вид имеет матрица

Матрица — это математический объект, который можно представить в виде таблицы с элементами, принадлежащими определенному кольцу или полю (например, целым, действительным или комплексным числам). Она состоит из строк и столбцов, где каждый элемент находится на пересечении соответствующей строки и столбца. Размер матрицы определяется количеством строк и столбцов. Таким образом, матрица может быть представлена прямоугольной таблицей.

Тип матрицы зависит от ее характеристик и может быть определен по ее размеру или по типу элементов, из которых она состоит. Например, квадратная матрица имеет одинаковое количество строк и столбцов, а диагональная матрица имеет ненулевые элементы только на главной диагонали. Различные типы матриц используются в различных областях математики и науки, таких как линейная алгебра, статистика и физика.

Какие зоны бывают в матрице судьбы

Матрица Судьбы — это система классификации жизненных областей, которые могут повлиять на нашу жизнь. Она включает в себя несколько зон: Детско-родительская карма, Духовно-творческая карма, Материальная карма прошлых жизней, Карма прошлых и партнерских отношений, Зона комфорта, Канал отношений, Канал финансов и Родовая линия отца. Каждая зона имеет свою собственную энергетику, которая определяет наше поведение и привлекаемые нами события. Например, ДРК может определять наше отношение к родителям и детям, а ДК — к нашей творческой деятельности. Каждая зона имеет свой потенциал и свои ограничения, и человек может успешно развиваться только тогда, когда умеет работать со всеми зонами своей Матрицы Судьбы. Это помогает ему достичь баланса и гармонии в жизни и стать успешным и счастливым человеком.

Простые операции с матрицами

Убрав минус из матрицы. Если большинство элементов в матрице имеют знак минус, это часто мешает вычислениям или приводит к ошибкам. Чтобы этого не произошло, избавьтесь от минуса. Для этого нужно переместить знак минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.

И наоборот: если внутри матрицы большинство элементов имеют знак минус, а перед матрицей стоит минус, то в матрицу можно вставить минус.

Вынимаем минус из матрицы и получаем вместо двадцати одного отрицательного элемента: четыре
Перед матрицей стоит минус, а внутри большинства элементов — минус. Введем в матрицу минус и сделаем ее удобной для дальнейших вычислений

Умножение матрицы на число. Чтобы умножить матрицу на число, просто умножьте каждый элемент матрицы на это число.

Пример умножения матрицы на число

Перестановка матриц. Это операция, которая нам понадобится позже для решения матричных уравнений. Для транспонирования мы берем известную матрицу, меняем местами строки столбцами и получаем новую матрицу. Как поставить матрицу на бок.

При этом запрещается изменять элементы матрицы в произвольном порядке. Но вы можете полностью поменять местами строки или столбцы. Если мы поменяем местами первую и вторую строки, останется та же матрица.

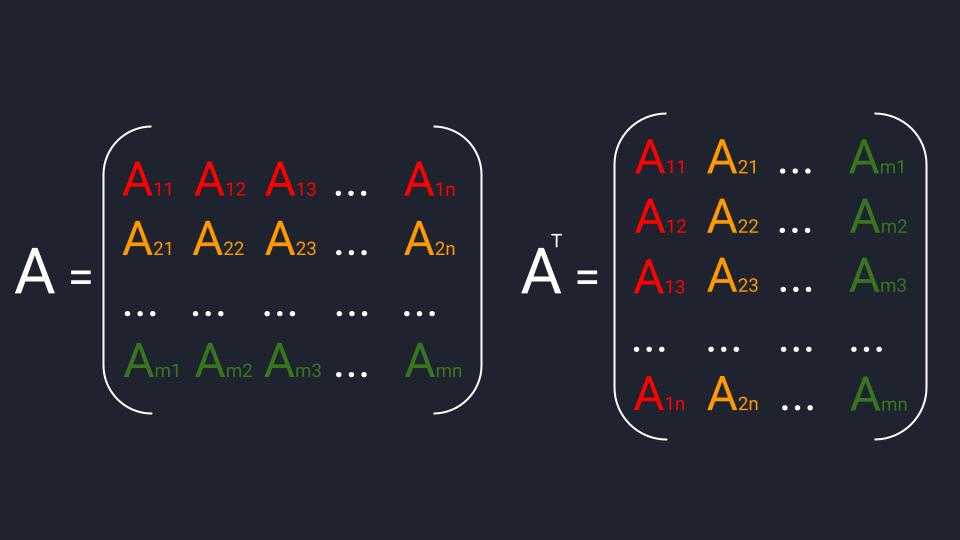
Схема транспонирования матрицы: первая строка переходит в первый столбец, вторая строка идет во второй столбец и так далее, в зависимости от количества элементов матрицы

Пример транспозиции. Транспонированная матрица обозначается буквой той же матрицы, из которой она была получена + верхний индекс в виде печатной буквы «Т»

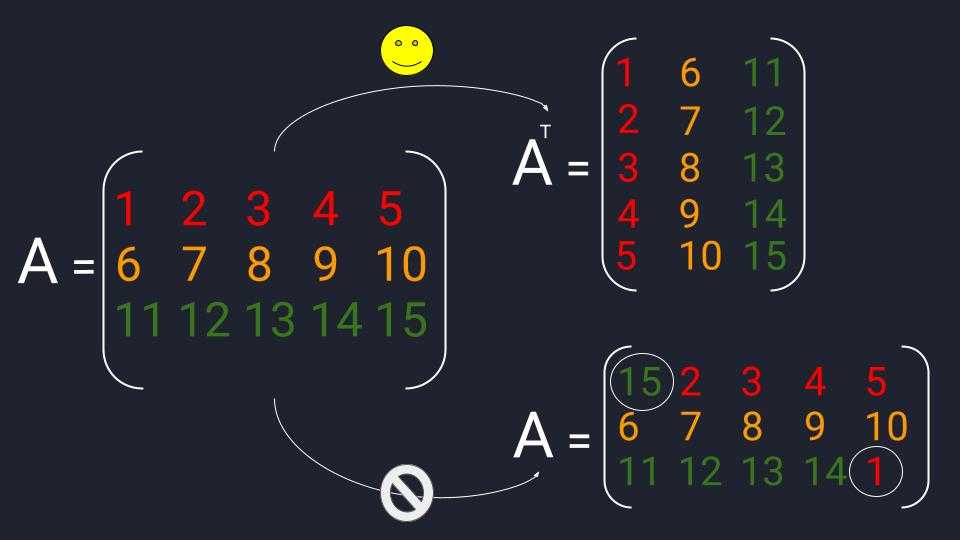
Матрицу можно смешивать, но делать это нужно по правилам. Транспонирование — одно из этих правил

Виды матриц в зависимости от их размера. Главная и побочная диагонали. След матрицы.

Пусть задана некая матрица $A_{m\times n}$. Если $m=1$ (матрица состоит из одной строки), то заданную матрицу называют матрица-строка. Если же $n=1$ (матрица состоит из одного столбца), то такую матрицу называют матрица-столбец. Например, $\left( \begin{array} {ccccc} -1 & -2 & 0 & -9 & 8 \end{array} \right)$ – матрица-строка, а $\left( \begin{array} {c} -1 \\ 5 \\ 6 \end{array} \right)$ – матрица-столбец.

Если для матрицы $A_{m\times n}$ верно условие $m\neq n$ (т.е. количество строк не равно количеству столбцов), то часто говорят, что $A$ – прямоугольная матрица. Например, матрица $\left( \begin{array} {cccc} -1 & -2 & 0 & 9 \\ 5 & 9 & 5 & 1 \end{array} \right)$ имеет размер $2\times 4$, т.е. содержит 2 строки и 4 столбца. Так как количество строк не равно количеству столбцов, то эта матрица является прямоугольной.

Если для матрицы $A_{m\times n}$ верно условие $m=n$ (т.е. количество строк равно количеству столбцов), то говорят, что $A$ – квадратная матрица порядка $n$. Например, $\left( \begin{array} {cc} -1 & -2 \\ 5 & 9 \end{array} \right)$ – квадратная матрица второго порядка; $\left( \begin{array} {ccc} -1 & -2 & 9 \\ 5 & 9 & 8 \\ 1 & 0 & 4 \end{array} \right)$ – квадратная матрица третьего порядка. В общем виде квадратную матрицу $A_{n\times n}$ можно записать так:

Говорят, что элементы $a_{11}$, $a_{22}$, $\ldots$, $a_{nn}$ находятся на главной диагонали матрицы $A_{n\times n}$. Эти элементы называются главными диагональными элементами (или просто диагональными элементами). Элементы $a_{1n}$, $a_{2 \; n-1}$, $\ldots$, $a_{n1}$ находятся на побочной (второстепенной) диагонали; их называют побочными диагональными элементами. Например, для матрицы $C=\left(\begin{array}{cccc}2&-2&9&1\\5&9&8& 0\\1& 0 & 4 & -7 \\ -4 & -9 & 5 & 6\end{array}\right)$ имеем:

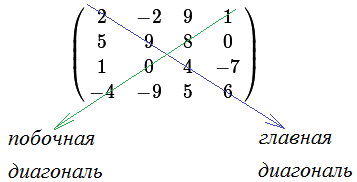
Элементы $c_{11}=2$, $c_{22}=9$, $c_{33}=4$, $c_{44}=6$ являются главными диагональными элементами; элементы $c_{14}=1$, $c_{23}=8$, $c_{32}=0$, $c_{41}=-4$ – побочные диагональные элементы.

Сумма главных диагональных элементов называется следом матрицы и обозначается $\Tr A$ (или $\Sp A$):

Например, для матрицы $C=\left(\begin{array} {cccc} 2 & -2 & 9 & 1\\5 & 9 & 8 & 0\\1 & 0 & 4 & -7\\-4 & -9 & 5 & 6 \end{array}\right)$ имеем:

Понятие диагональных элементов используется также и для неквадратных матриц. Например, для матрицы $B=\left( \begin{array} {ccccc} 2 & -2 & 9 & 1 & 7 \\ 5 & -9 & 8 & 0 & -6 \\ 1 & 0 & 4 & -7 & -6 \end{array} \right)$ главными диагональными элементами будут $b_{11}=2$, $b_{22}=-9$, $b_{33}=4$.

Пример теоретической части диплома

Независимо от того какой путь выбран, образец теоретической главы дипломной работы поможет выстроить ориентиры, но не забывайте: чтобы пройти «Антиплагиат», способ написания «Ctrl+C – Ctrl+V» – заведомо проигрышный.

Теоретическая часть диплома – пример:

• по пищевым технологиям;
• педагогике (начальная школа);
• менеджменту;
• маркетингу.

Углубляясь в анализ опыта предшественников, занимавшихся исследованием темы, ориентируйтесь на рекомендуемый объем теоретической части диплома – примерно 2/3 практического раздела. Стандарт не стоит превышать, иначе работа превратится в реферат.

Автор статьи:

Определение матрицы и её элемента. Обозначения.

Матрица – это таблица из $m$ строк и $n$ столбцов. Элементами матрицы могут быть объекты совершенно разнообразной природы: числа, переменные или, к примеру, иные матрицы. Например, матрица $\left( \begin{array} {cc} 5 & 3 \\ 0 & -87 \\ 8 & 0 \end{array} \right)$ содержит 3 строки и 2 столбца; элементами её являются целые числа. Матрица $\left(\begin{array} {cccc} a & a^9+2 & 9 & \sin x \\ -9 & 3t^2-4 & u-t & 8\end{array} \right)$ содержит 2 строки и 4 столбца.

Разные способы записи матриц: показать\скрыть

Произведение $m\times n$ называют размером матрицы. Например, если матрица содержит 5 строк и 3 столбца, то говорят о матрице размера $5\times 3$. Матрица $\left(\begin{array}{cc} 5 & 3\\0 & -87\\8 & 0\end{array}\right)$ имеет размер $3 \times 2$.

Обычно матрицы обозначаются большими буквами латинского алфавита: $A$, $B$, $C$ и так далее. Например, $B=\left( \begin{array} {ccc} 5 & 3 \\ 0 & -87 \\ 8 & 0 \end{array} \right)$. Нумерация строк идёт сверху вниз; столбцов – слева направо. Например, первая строка матрицы $B$ содержит элементы 5 и 3, а второй столбец содержит элементы 3, -87, 0.

Элементы матриц обычно обозначаются маленькими буквами. Например, элементы матрицы $A$ обозначаются $a_{ij}$. Двойной индекс $ij$ содержит информацию о положении элемента в матрице. Число $i$ – это номер строки, а число $j$ – номер столбца, на пересечении которых находится элемент $a_{ij}$. Например, на пересечении второй строки и пятого столбца матрицы

расположен элемент $a_{25}=59$:

Точно так же на пересечении первой строки и первого столбца имеем элемент $a_{11}=51$; на пересечении третьей строки и второго столбца – элемент $a_{32}=-15$ и так далее. Замечу, что запись $a_{32}$ читается как «а три два», но не «а тридцать два».

Для сокращённого обозначения матрицы $A$, размер которой равен $m\times n$, используется запись $A_{m\times n}$. Нередко используется и такая запись:

Здесь $(a_{ij})$ указывает на обозначение элементов матрицы $A$, т.е. говорит о том, что элементы матрицы $A$ обозначаются как $a_{ij}$. В развёрнутом виде матрицу $A_{m\times n}=(a_{ij})$ можно записать так:

Введём еще один термин – равные матрицы.

Две матрицы одинакового размера $A_{m\times n}=(a_{ij})$ и $B_{m\times n}=(b_{ij})$ называются равными, если их соответствующие элементы равны, т.е. $a_{ij}=b_{ij}$ для всех $i=\overline{1,m}$ и $j=\overline{1,n}$.

Пояснение к записи $i=\overline{1,m}$: показать\скрыть

Итак, для равенства матриц требуется выполнение двух условий: совпадение размеров и равенство соответствующих элементов. Например, матрица $A=\left(\begin{array}{cc} 5 & 3\\0 & -87\\8 & 0\end{array}\right)$ не равна матрице $B=\left(\begin{array}{cc} 8 & -9\\0 & -87 \end{array}\right)$, поскольку матрица $A$ имеет размер $3\times 2$, а размер матрицы $B$ составляет $2\times 2$. Также матрица $A$ не равна матрице $C=\left(\begin{array}{cc} 5 & 3\\98 & -87\\8 & 0\end{array}\right)$, поскольку $a_{21}\neq c_{21}$ (т.е. $0\neq 98$). А вот для матрицы $F=\left(\begin{array}{cc} 5 & 3\\0 & -87\\8 & 0\end{array}\right)$ можно смело записать $A=F$ поскольку и размеры, и соответствующие элементы матриц $A$ и $F$ совпадают.

Пример №1

Определить размер матрицы
$A=\left(\begin{array} {ccc} -1 & -2 & 1 \\
5 & 9 & -8 \\
-6 & 8 & 23 \\
11 & -12 & -5 \\
4 & 0 & -10 \\
\end{array} \right)$. Указать, чему равны элементы $a_{12}$, $a_{33}$, $a_{43}$.

Решение

Данная матрица содержит 5 строк и 3 столбца, поэтому размер её $5\times 3$. Для этой матрицы можно использовать также обозначение $A_{5\times 3}$.

Элемент $a_{12}$ находится на пересечении первой строки и второго столбца, поэтому $a_{12}=-2$. Элемент $a_{33}$ находится на пересечении третьей строки и третьего столбца, поэтому $a_{33}=23$. Элемент $a_{43}$ находится на пересечении четвертой строки и третьего столбца, поэтому $a_{43}=-5$.

Ответ: $a_{12}=-2$, $a_{33}=23$, $a_{43}=-5$.

Что такое теоретическая часть диплома

Дипломная работа традиционно состоит из нескольких блоков, один из них – теоретическая часть, которая следует за введением и предваряет практическую главу, более детально описывающую тему работы или посвященную доказательству и фактической аргументации выдвинутой гипотезы. Если расчетно-аналитический раздел не предусмотрен, то в первой части автор должен описать центральные идеи и тезисы, которые будут рассматриваться и анализироваться в основном блоке диплома.

Чтобы максимально информативно описать академическую базу работы, при подготовке теоретической главы студент должен опираться на профильные научные труды, публикации и исследования, делая на них ссылки в тексте.

Умножение матриц

Массивы перемножаются по столбцу. Мы умножаем первую строку первой матрицы на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. Аналогичным образом рассчитываем все остальные элементы. Смотрится запутанно, так что давайте пошагово:

1. У нас есть две матрицы A и B. Нам нужно перемножить их, чтобы получить новую матрицу C.
2. Размер матрицы A — два на два: две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; второй — А₂₁ и А₂₂.
3. Матрица B имеет такой же размер: в ней две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; второй — B₂₁ и B₂₂.
4. У нас есть две матрицы одинакового размера с двумя строками и двумя столбцами. Это означает, что матрица C будет размером два на два. Первая строка будет C₁₁ и C₁₂; второй — C₂₁ и C₂₂.
5. Рассмотрим элемент C₁₁. Умножаем первый элемент первой строки матрицы A (A₁₁) на первый элемент первого столбца матрицы B (B₁₁). Это первая часть, после которой ставим знак плюса. Вторая часть: умножьте второй элемент первой строки матрицы A (A₁₂) на второй элемент первого столбца матрицы B (B₂₁). Складываем обе стороны и получаем первый элемент первой строки матрицы C (C₁₁).
6. Рассмотрим элемент C₁₂. Умножаем первый элемент первой строки матрицы A (A₁₁) на первый элемент второго столбца матрицы B (B₁₂). Это первая часть. Вторая часть: умножьте второй элемент первой строки матрицы A (A₁₂) на второй элемент второго столбца матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы C (C₁₂).
7. Рассмотрим элемент C₂₁. Умножаем первый элемент второй строки матрицы A (A₂₁) на первый элемент первого столбца матрицы B (B₁₁). Это первая часть. Вторая часть: умножьте второй элемент второй строки матрицы A (A₂₂) на второй элемент первого столбца матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы C (C₂₁).
8. Рассмотрим элемент C₂₂. Умножаем первый элемент второй строки матрицы A (A₂₁) на первый элемент второго столбца матрицы B (B₁₂). Это первая часть. Вторая часть: умножьте второй элемент второй строки матрицы A (A₂₂) на второй элемент второго столбца матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы C (C₂₂).

Если нам нужно найти квадратную матрицу, мы умножаем эту матрицу на себя. Если вам нужна матрица в кубе, мы умножаем ее на себя трижды и так далее, в зависимости от количества градусов. Если в одной из матриц все элементы равны нулю, тогда она считается нулевой, и после умножения на другую матрицу она дает нулевую матрицу — это похоже на то, что умножение нуля на число всегда дает ноль.

Формула умножения матриц
Пример умножения квадратных матриц размера 2 × 2

Некоторые виды матриц.

Введем определения некоторых часто употребляемых видов матриц. Все матрицы предполагаются квадратными.

Определение.

Матрица \(A\) называется симметричной или симметрической, если \(A^{T}=A\). Для такой матрицы \(a_{ij}=a_{ji}\) при всех \(i\) и \(j\) — элементы, расположенные симметрично относительно главной диагонали, равны.

Определение.

Матрица \(A\) называется кососимметричной или антисимметричной, если \(A^{T}=-A\). Для такой матрицы \(a_{ij}=-a_{ji}\) при всех \(i\) и \(j\) — элементы, расположенные симметрично относительно главной диагонали, отличаются знаком. Диагональные элементы равны нулю.

Определение.

Матрица \(A\) называется верхней треугольной, если ее элементы, расположенные ниже главной диагонали, равны нулю: \(a_{ij}=0\) при \(i > j\). Аналогично определяется нижняя треугольная матрица: \(a_{ij}=0\) при \(i < j\).

Определение.

Матрица \(A\) называется диагональной, если у нее равны нулю все недиагональные элементы: \(a_{ij}=0\) при \(i \neq j\).

Другие частные виды матриц будем определять по мере необходимости.

Понятие определителя n-го порядка

Пользуясь этой статьёй об определителях, вы обязательно научитесь решать задачи вроде следующей:

Решить уравнение:

и многих других, которые так любят придумывать преподаватели.

Определитель матрицы или просто определитель играет важную роль в решении систем линейных уравнений. В общем-то определители и были придуманы для
этой цели. Поскольку часто говорят также «определитель матрицы», упомянем здесь и матрицы. Матрица — это прямоугольная таблица, составленная из чисел, которые нельзя менять местами.
Квадратная матрица — таблица, у которой число строк и число столбцов одинаково. Определитель может быть только у квадратной матрицы.

Понять логику записи определителей легко по следующей схеме. Возьмём знакомую вам со школьной скамьи
систему из двух уравнений с двумя неизвестными:

В определителе последовательно записываются коэффициенты при неизвестных: в первой строке — из первого уравнения,
во второй строке — из второго уравнения:

Например, если дана система уравнений

,

то из коэффициентов при неизвестных формируется следующий определитель:

Итак, пусть дана квадратная таблица, состоящая из чисел, расположенных в n строках (горизонтальных рядах) и в n столбцах (вертикальных рядах). С помощью этих чисел по некоторым правилам, которые мы изучим ниже, находят число, которое и называют определителем n-го порядка и обозначают следующим образом:

                    (1)

Числа называют
элементами определителя (1) (первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит элемент; i = 1, 2, …, n;  j = 1, 2, …, n). Порядок определителя – это число его строк и столбцов.

Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы

называется главной диагональю, другая диагональ – побочной.

По теме «Определители» на сайте есть
также отдельный урок по вычислению минора и алгебраического дополнения.

Виды матриц в зависимости от значений их элементов.

Если все элементы матрицы $A_{m\times n}$ равны нулю, то такая матрица называется нулевой и обозначается обычно буквой $O$. Например, $\left( \begin{array} {cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right)$, $\left( \begin{array} {ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)$ – нулевые матрицы.

Рассмотрим некоторую ненулевую строку матрицы $A$, т.е. такую строку, в которой есть хоть один элемент, отличный от нуля. Ведущим элементом ненулевой строки назовём её первый (считая слева направо) ненулевой элемент. Для примера рассмотрим такую матрицу:

Во второй строке ведущим будет четвёртый элемент, т.е. $w_{24}=12$, а в третьей строке ведущим будет второй элемент, т.е. $w_{32}=-9$.

Матрица $A_{m\times n}=\left(a_{ij}\right)$ называется ступенчатой, если она удовлетворяет двум условиям:

1. Нулевые строки, если они есть, расположены ниже всех ненулевых строк.
2. Номера ведущих элементов ненулевых строк образуют строго возрастающую последовательность, т.е. если $a_{1k_1}$, $a_{2k_2}$, …, $a_{rk_r}$ – ведущие элементы ненулевых строк матрицы $A$, то $k_1\lt{k_2}\lt\ldots\lt{k_r}$.

Примеры ступенчатых матриц:

Для сравнения: матрица $Q=\left(\begin{array}{ccccc} 2 & -2 & 0 & 1 & 9\\0 & 0 & 0 & 7 & 9\\0 & -5 & 0 & 10 & 6\end{array}\right)$ не является ступенчатой, так как нарушено второе условие в определении ступенчатой матрицы. Ведущие элементы во второй и третьей строках $q_{24}=7$ и $q_{32}=10$ имеют номера $k_2=4$ и $k_3=2$. Для ступенчатой матрицы должно быть выполнено условие $k_2\lt{k_3}$, которое в данном случае нарушено. Отмечу, что если поменять местами вторую и третью строки, то получим ступенчатую матрицу: $\left(\begin{array}{ccccc} 2 & -2 & 0 & 1 & 9\\0 & -5 & 0 & 10 & 6 \\0 & 0 & 0 & 7 & 9\end{array}\right)$.

Ступенчатую матрицу называют трапециевидной или трапецеидальной, если для ведущих элементов $a_{1k_1}$, $a_{2k_2}$, …, $a_{rk_r}$ выполнены условия $k_1=1$, $k_2=2$,…, $k_r=r$, т.е. ведущими являются диагональные элементы. В общем виде трапециевидную матрицу можно записать так:

Примеры трапециевидных матриц:

Дадим ещё несколько определений для квадратных матриц. Если все элементы квадратной матрицы, расположенные под главной диагональю, равны нулю, то такую матрицу называют верхней треугольной матрицей. Например, $\left( \begin{array} {cccc} 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & 6 \end{array} \right)$ – верхняя треугольная матрица. Заметьте, что в определении верхней треугольной матрицы ничего не сказано про значения элементов, расположенных над главной диагональю или на главной диагонали. Они могут быть нулевыми или нет, – это несущественно. Например, $\left( \begin{array} {ccc} 0 & 0 & 9 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right)$ – тоже верхняя треугольная матрица.

Если все элементы квадратной матрицы, расположенные над главной диагональю, равны нулю, то такую матрицу называют нижней треугольной матрицей. Например, $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ -5 & 1 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 6 \end{array} \right)$ – нижняя треугольная матрица. Заметьте, что в определении нижней треугольной матрицы ничего не сказано про значения элементов, расположенных под или на главной диагонали

Они могут быть нулевыми или нет, – это неважно. Например, $\left( \begin{array} {ccc} -5 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 9 \end{array} \right)$ и $\left( \begin{array} {ccc} 0 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right)$ – тоже нижние треугольные матрицы

Квадратная матрица называется диагональной, если все элементы этой матрицы, не лежащие на главной диагонали, равны нулю. Пример: $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 \end{array} \right)$. Элементы на главной диагонали могут быть любыми (равными нулю или нет), – это несущественно.

Диагональная матрица называется единичной, если все элементы этой матрицы, расположенные на главной диагонали, равны 1. Например, $\left(\begin{array} {cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$ – единичная матрица четвёртого порядка; $\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array}\right)$ – единичная матрица второго порядка.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Обратные «модели»

Обратная матрица тоже встречается при решении задач. Вырожденная «модель» — это квадратный объект строк и столбцов n-го порядка, когда определитель равен нулю. Невырожденная – когда не равен ему соответственно.

Матрица A-1 – обратная, если для нее актуально соотношение типа: A x A-1=A-1 x A = E.

Если A-1 не вырождена, то существует всего одна обратная матрица A-1. Она будет равна значению:

А вот несколько наглядных примеров:

Как найти

Для того, чтобы определить A-1, необходимо:

• Найти детерминант A.
• Проверить, чтобы он не был равен нулю.
• Найти миноры матрицы – M_ij.
• Определить A_ij= (-1)i+jM_ij.
• Построить матрицу алгебраических дополнений:

Поделить каждое из слагаемых (каждый элемент матрицы) объекта на детерминант A.

Умножение числа на матрицу, как и другие операции – это не так трудно. Зная соответствующую базу, человек сможет производить вручную или через специальные калькуляторы необходимые подсчеты. А некоторые видео уроки объяснят теорию простым языком.

Знакомство с матрицами

Понятие и базовые операции.

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

• Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного.
• У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
• Векторы можно складывать, вычитать, умножать. Это чуть сложнее, чем с обычными числами.
• У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.

Принцип написания

В теоретической части больше всего ценится ее научная новизна. Это значит, что студент должен не только проанализировать и переписать своими словами чужие труды: статьи, монографии, диссертации, архивные публикации, документы или интервью – но и на основе анализа собранного материала внести что-то новое в науку, добавляя свои находки и рассуждения.

При написании теоретической части диплома важны выводы. Они показывают, что студент не только изучил источники, но и проанализировал их, сделал определенные заключения, которые могут быть двух видов:

промежуточные – логически завершают отдельные блоки главы, представляют собой результаты осмысления приведенных цитат, рассмотренных исследований или идей;

глобальные комплексного типа – размещаются в конце теоретической главы диплома, могут содержать подпункты, в которых разъясняются завершающие мысли и тезисы.

Просто суммировать промежуточные выводы в финале – проигрышный вариант. В идеале надо прочитать работу еще раз и дать ответы на вопросы теоретической части диплома, которые помогут настроиться на основной раздел и перекинут логический мостик между составляющими исследования.

Универсальный способ завершить главу с теорией – подчеркнуть, что тема недостаточно изучена, и именно это подтолкнуло автора к ее обстоятельной разработке.

Математические методы научного исследования: описание

Использование грамотных методов в исследовании — это залог успеха. Но чтобы не ошибиться в выборе, нужно понимать, что из себя представляют методические приёмы и для каких задач они подходят.

Главная задача студента — из всего многообразия математических методов выбрать те, которые помогут раскрыть тему исследования и достичь поставленных целей и задач. Так что очень внимательно отнеситесь к этому вопросу. А если не можете определиться сами — обратитесь к научному руководителю.

Давайте кратко рассмотрим самые популярные методы, которые применяют в математике, и разберёмся в их специфике.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы.

Применение матриц в математико-экономическом моделировании

В виде матриц просто и удобно записываются структурированные данные о том или ином объекте. Матричные
модели создаются не только для хранения этих структурированных данных, но и для решения различных задач с этими данными
средствами линейной алгебры.

Так, известной матричной моделью экономики является модель «затраты-выпуск», внедрённая американским
экономистом русского происхождения Василием Леонтьевым. Эта модель исходит из предположения, что весь производственный
сектор экономики разбит на n чистых отраслей. Каждая из отраслей выпускает продукцию только одного вида и разные отрасли
выпускают разную продукцию. Из-за такого разделения труда между отраслями существуют межотраслевые связи, смысл которых
состоит в том, что часть продукции каждой отрасли передаётся другим отраслям в качестве ресурса производства.

Объём продукции i-й отрасли (измеряемый определённой единицей измерения), которая была произведена
за отчётный период, обозначается через и
называется полным выпуском i-й отрасли. Выпуски
удобно разместить в n-компонентную строку матрицы.

Количество единиц продукции i-й отрасли, которое необходимо затратить j-й
отрасли для производства единицы своей продукции, обозначается
и называется коэффициентом прямых затрат.

Коэффициенты прямых затрат ,
среди которых многие могут равняться нулю, удобно записать в nxn матрицу коэффициентов прямых затрат:

Матрица содержит много информации о структуре межотраслевых связей. При этом j-й
столбец матрицы полностью характеризует затраты j-й отрасли для производства единицы продукции.

Пример 4. На некоторой благоустроенной исследовательской странции в Арктике
действуют три отрасли производства. Первая из них — небольшая электростанция, производящая электроэнергию. Вторая —
установка для производства пресной воды из снега. Третья — хлебопекарня.

Записать в матрицу коэффициентов прямых затрат данные о том, что 0,10 единиц электроэнергии расходуется
для производства одной единицы электроэнергии, 0,40 единиц электроэнергии расходуется для производства одной единицы
пресной воды, 0,30 единиц электроэнергии расходуется для производства одной единицы хлебопродуктов;
0,05 единиц пресной воды расходуется для производства одной единицы электроэнергии, 0 единиц пресной воды расходуется
на производство одной единицы пресной воды, 0,20 единиц пресной воды расходуется на производство одной единицы хлебопродуктов;
затраты же хлебопродуктов на производство всех видов продукции, включая хлебопродукту равны нулю.

Решение. Записываем коэффициенты затрат каждой отрасли в свою строку: электростанции — в первую,
установки для производства пресной воды — во вторую, хлебопекарни — в третью. Получаем искомую матрицу:

Матрицы оказались очень востребованной структурой данных в программировании и вообще
в информационных технологиях. В частности, такие объекты, как графы, в памяти компьютера часто задаются
в форме матриц смежности и матриц инцидентности. Кроме того,
матрицы очень удобны для формализации многих ситуаций в бизнесе и жизни вообще, задачи на которые решаются
в теории игр.

Назад

Листать

Вперёд>>>

Продолжение темы «Матрицы»

Другие темы линейной алгебры

Виды матриц

1. Если матрица состоит из одной строки, она называется вектор-строкой (или матрицей-строкой).

2. Матрица, состоящая из одного столбца, называется вектором-столбцом (или матрицей-столбцом).

3. Квадратная – матрица, которая содержит одинаковое количество строк и столбцов, т.е. m (строки) равняется n (столбцы). Размер матрицы можно задать как n x n или m x m , где m (n) – ее порядок.

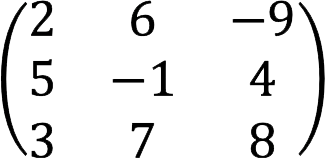
4. Нулевая – матрица, все элементы которой равняются нулю ( a_ij = 0).

5. Диагональная – квадратная матрица, у которой все элементы, за исключением расположенных на главной диагонали, равняются нулю. Одновременно является верхней и нижней треугольной.

6. Единичная – это разновидность диагональной матрицы, у которой все элементы главной диагонали равны единице. Обычно обозначается буквой E.

7. Верхняя треугольная – все элементы матрицы ниже главной диагонали равны нулю.

8. Нижняя треугольная – матрица, все элементы которой выше главной диагонали равняются нулю.

9. Ступенчатая – матрица, для которой выполняются следующие условия:

• если в матрице есть нулевая строка, то все остальные строки, находящиеся под ней, являются нулевыми.
• если первый ненулевой элемент определенной строки находится в столбце с порядковым номером j , и следующая строка является ненулевой, то первый ненулевой элемент следущей строки должен располагаться в столбце с номером больше, чем j .

Виды матриц

Вот некоторые основные виды матриц:

Квадратная матрица: Матрица, у которой количество строк равно количеству столбцов. Например, матрица размером 3×3 или 4×4;

• Прямоугольная матрица: Матрица, у которой количество строк и количество столбцов различны. Например, матрица размером 3×4 или 2×5;
• Нулевая матрица: Матрица, все элементы которой равны нулю;
• Единичная матрица: Квадратная матрица, у которой все элементы на главной диагонали равны единице, а остальные элементы равны нулю;
• Диагональная матрица: Квадратная матрица, у которой все элементы вне главной диагонали равны нулю. Элементы на главной диагонали могут быть любыми;
• Верхнетреугольная матрица: Квадратная матрица, у которой все элементы ниже главной диагонали равны нулю;
• Нижнетреугольная матрица: Квадратная матрица, у которой все элементы выше главной диагонали равны нулю;
• Симметричная матрица: Квадратная матрица, которая равна своему транспонированию. Значит, элементы отражаются относительно главной диагонали;
• Транспонированная матрица: Матрица, полученная путем замены строк на столбцы и столбцов на строки исходной матрицы;
• Скалярная матрица: Матрица, все элементы которой равны одному и тому же числу (скаляру).

Это лишь несколько примеров типов матриц, и существует еще множество других видов матриц, включая треугольные, блочные и разреженные матрицы. Каждый тип матрицы имеет свои особенности и применяется в различных математических и прикладных областях.

Заключение

Хорошая демонстрация продукта поможет вам квалифицировать лидов и превратить потенциальных клиентов в реальных. Однако ни один из примеров, которые мы использовали в этой статье, не делает упор на продажу

Вместо этого бренды уделяют основное внимание тому, как продукт решает проблемы клиентов, так как только это помогает наладить связь с аудиторией и приблизить к закрытию сделки

Используйте примеры из этой статьи как источник вдохновения для создания своих собственных демонстраций. Подумайте, чем наиболее ценен ваш продукт, на кого вы хотите ориентироваться и что беспокоит ваших клиентов. Это даст вам представление о том, какой тип демонстрации лучше всего выбрать.

Если ваш продукт является многофункциональным или требует длительного обучения пользователей, наиболее полезной может оказаться живая демонстрация или предварительно записанная демонстрация, проведенная под руководством члена вашей команды. Если он прост в использовании, короткая видеоанимация или онбординг, реализованный, например, с помощью такого инструмента, как Experrto, могут лучше подойти для убеждения потенциальных клиентов. С его помощью вы можете не только обратиться к клиентам и «провести» их через ваш продукт, но и предоставить нужную помощь в нужное время, тем самым значительно сократив количество обращений в службу поддержки.

Какой вариант вы бы ни выбрали, следуйте ключевым принципам: квалифицируйте лидов, тщательно готовьтесь и ведите клиентов по всему пути — от знакомства до решения конкретных задач и последующих шагов.

Подписывайтесь на нашу группу в фейсбуке и канал в телеграм, чтобы следить за обновлениями.

Прокачайте свой онбординг!