Как найти область определения и область значений функции

Примеры решения

Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.

С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.

Для линейного вида

Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:

1. Упростить выражение.
2. Определить D (f).

Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = — x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика.

В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.

Дробные и иррациональные

Пусть существует выражение вида y = 1 / . Нужно определить D (f).

Решается задача таким способом:

1. Приравнивается знаменатель к 0.
2. Решается уравнение.
3. Определяется интервал допустимых значений.

Нужно решить уравнение (x — 4) * (x + 4) = 0. Из него видно, что x1 = 4 и x2 = -4, поскольку эти значения «превращают» знаменатель в неопределенность. Следовательно, D (y) = (-бесконечность, -4) U (4, +бесконечность).

В случае с иррациональным выражением: y = sqrt, нужно решить уравнение подкоренного выражения.

Для решения квадратного уравнения следует применить такой алгоритм:

1. Записать неравенство: 4 * sqr (x) — 12 * x + 9 >= 0.
2. Дискриминант: D = — (4 * a * c) = — (4 * 4 * 9) = 144 — 144 = 0.
3. D = 0 — только одно решение.
4. x = (-b) / (2 * a) >= 12 / (2 * 4) >= 12 / 8 >= 6 / 4 >= 1,5.

Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.

Как найти область значений функции по уравнению

Нахождение области значений функции по заданному уравнению также сводится к вычислению экстремумов.

Рассмотрим два случая:

1. Нахождение области значений функции, непрерывной на некотором заданном отрезке.
2. Нахождение области значений функции, непрерывной на некотором интервале. Сюда же отнесем случаи, когда функция не существует в какой-либо точке. Например, точка нуля знаменателя, в которой функция не существует, а область определения терпит разрыв.

Алгоритм поиска области значений для первого случая:

1. Находим производную функции.
2. Приравниваем производную к нулю, находим корни уравнения f′(x)=0 и точки, в которых производная не существует — критические точки.
3. Отмечаем корни, критические точки и границы заданного интервала на прямой и определяем знаки производной на каждом получившемся промежутке.
4. Находим минимумы и максимумы функции. Если в некоторой точке x1 производная меняет знак с «+» на «-», то точка x1 — максимум, если с «-» на «+» — минимум.
5. Подставляя значения аргументов для минимума и максимума функции в выражение f(x), находим минимальное и максимальное значения функции. В том случае, если имеются точки, в которых производная не существует, значение функции вычисляем через пределы по формулам: limx→x1—f(x)   и limx→x1+f(x).
6. Записываем область значений функции.

Для второго случая:

1. Находим производную, приравниваем ее к нулю и определяем знаки производной на каждом промежутке.
2. Определяем значение функции в каждой из точек. Для определения значения функции в граничных точках, а также в точках разрыва или точках, в которых производная не существует, вычисляем пределы функции аналогично указанным в пункте 5 для первого случая.
3. Определяем и записываем область значений.

Область определения это:

Запрос «Отображение» перенаправляется сюда. Cм. также другие значения

В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.

Определения

• Нестрогое определение: функция — это «закон», по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
• Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:

Функция называется инъективной, если

Обозначения

• , или для отображения F множества X в множество Y;
  • Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или .).
  • Множество Y называется о́бластью значе́ний отображения F.(обозначается E(F), или ).
• , y = F(x) или или . Используется также обратная польская запись: y = xF, а иногда y = xF

  Элементы x называют аргументами функции, а соответствующие элементы y — значениями функции.

  .

Связанные определения

Пусть дано отображение , и . Тогда суже́нием функции F на M называется функция , определяемая равенством . Это определение подчёркивает, что фиксация области определения является частью определения функции.

F является продолжением функции на множество . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.

Пусть . Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством .

FXF

• Пусть задано отображение , и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент должен иметь ровно один образ, но элемент

  Например, пусть дана функция , где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.

  может не иметь прообразов либо иметь один или несколько.

• Пусть задано отображение , и . Тогда множество называется по́лным проо́бразом элемента y. Полный прообраз обозначается F — 1(y

  Например, пусть , и F(x) = sinx. Тогда .

  ).

• Пусть . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством

  Например, пусть , и F(x) = cosx. Тогда , .

  .

• ;
• ;
• ;
• . Заметим отсутствие равенства в этом случае.

Классы функций

При необходимости можно различать отображения в зависимости от природы множеств X и Y. Если X и Y — числовые множества, такие, как

XYве́ктор-фу́нкциейXYфункциона́лом

Вариации и обобщения

многозначная функция

Функции нескольких аргументов

Определение функции легко обобщить на случай функции многих аргументов.

Пусть даны множества

Yn

См. также

• Композиция функций
• График функции
• Сюръективность
• Инъективность
• Биективность
• Функция с множеством значений {0, 1}
• Функциональное уравнение

Литература

Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.

Wikimedia Foundation. 2010.

dic.academic.ru

Методы нахождения

Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.

Перебор значений

Самый простой и ограниченный способ. При его помощи можно находить область значений на небольшом промежутке целых чисел \(x\in(a;\;b)\). В таком случае заданные значения переменной поочередно подставляются в уравнение и вычисляются значения функции, соответствующие им.

Графический метод

Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.

Примечание

Если по условию задачи необходимо найти область значений функции на определенном промежутке значений переменной x, то на графике максимальные и минимальные точки становятся очевидными. Это могут быть как общие точки экстремума, так и локальные максимальные и минимальные значения.

Учет непрерывности и монотонности

Данный метод вытекает из предыдущего и позволяет делать некоторые прогнозы об области значений функции исходя из ее свойств. Если на графике видно, что функция не прерывается и монотонно убывает или возрастает на определенном промежутке, можно предположить, что эта тенденция сохранится и дальше.

Например, график квадратичной функции f(x)=x^2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем \(x\in\lbrack-4;\;4\rbrack\):

Рисунок 1. Значение непрерывности и монотонности функции для области определения

На графике видно, что функция монотонно убывает на промежутке \(\lbrack-4;\;0\rbrack\) и монотонно возрастает на промежутке\( \lbrack0;\;4\rbrack\). Исходя из этого и непрерывности функции, можно экстраполировать данную закономерность на всю область определения. Так как минимальное значение данной функции равняется нулю, область значений будет следующей:

\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty)\)

Производная, min и max

Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.

Определение

Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.

Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными

Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:

• если при переходе через критическую точку производная функции меняет знак с (+) на (-), то эта точка является максимумом;
• если при переходе через критическую точку производная меняет знак с (-) на (+), то такая точка является минимумом;
• если при переходе знак производной не меняется, то экстремума в данной точке нет.

Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:

Если \(f»(x_1)>0\), то \(x_1\) — точка минимума.

Если \(f»(x_1)<0\), то \(x_1\) — точка максимума.

Область определения функции с логарифмом

Третья распространённая функция – логарифм. В качестве образца я буду рисовать натуральный логарифм, который попадается примерно в 99 примерах из 100. Если некоторая функция содержит логарифм , то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству . Если логарифм находится в знаменателе: , то дополнительно накладывается условие  (так как ).

Пример 9

Найти область определения функции

Решение: в соответствии с вышесказанным составим и решим систему:

Графическое решение для чайников:Ответ: область определения:

Остановлюсь ещё на одном техническом моменте – у меня ведь не указан масштаб и не проставлены деления по оси. Возникает вопрос: как выполнять подобные чертежи в тетради на клетчатой бумаге? Отмерять ли расстояние между точками по клеточкам строго по масштабу? Каноничнее и строже, конечно, масштабировать, но вполне допустим и схематический чертёж, принципиально отражающий ситуацию.

Пример 10

Найти область определения функции

Для решения задачи можно использовать метод предыдущего параграфа – проанализировать, как парабола расположена относительно оси абсцисс. Ответ в конце урока.

Как видите, в царстве логарифмов всё очень похоже на ситуацию с квадратным корнем: функция  (квадратный трёхчлен из Примера № 7) определена на интервалах , а функция  (квадратный двучлен из Примера № 6) на интервале . Неловко уже и говорить, функции типа  определены на всей числовой прямой.

Полезная информация: интересна типовая функция , она определена на всей числовой прямой кроме точки . Согласно свойству логарифма , «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» необходимо заключить под знак модуля: . Вот вам и ещё одно «практическое применение» модуля = ). Так необходимо поступать в большинстве случаев, когда вы снОсите чётную степень, например: .  Если же основание степени  заведомо положительно, например, , то в знаке модуля отпадает необходимость и достаточно обойтись круглыми скобками: .

Чтобы не повторяться, давайте усложним задание:

Пример 11

Найти область определения функции

Решение: в данной функции у нас присутствует и корень и логарифм.

Подкоренное выражение должно быть неотрицательным: , а выражение под знаком логарифма – строго положительным: . Таким образом, необходимо решить систему:

Многие из вас прекрасно знают или интуитивно догадываются, что решение системы должно удовлетворять каждому условию.

Исследуя расположение параболы  относительно оси , приходим к выводу, что неравенству  удовлетворяет интервал  (синяя штриховка):
Неравенству , очевидно, соответствует «красный» полуинтервал  .

Поскольку оба условия должны выполняться одновременно, то решением системы является пересечение данных интервалов. «Общие интересы» соблюдены на полуинтервале .

Ответ: область определения:

Типовое неравенство , как демонстрировалось в Примере № 8,  нетрудно разрешить и аналитически.

Найденная область определения не изменится для «похожих функций», например, для  или .  Также можно добавить какие-нибудь непрерывные на  функции, например: , или так: , или даже так: . Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится (хотя в общем случае это не всегда справедливо). Ну а в теории матана по поводу этого словесного… ой… существуют теоремы.

Пример 12

Найти область определения функции

Это пример для самостоятельного решения. Использование чертежа вполне уместно, так как функция не самая простая.

Ещё пару примеров для закрепления материала:

Пример 13

Найти область определения функции

Решение: составим и решим систему:
Все действия уже разобраны по ходу статьи. Изобразим на числовой прямой интервал, соответствующий неравенству  и, согласно второму условию, исключим две точки:
Значение  оказалось вообще не при делах.

Ответ: область определения

Небольшой математический каламбур на вариацию 13-го примера:

Пример 14

Найти область определения функции

Это пример для самостоятельного решения. Кто пропустил, тот в пролёте

Завершающий раздел урока посвящен более редким, но тоже «рабочим» функциям:

Область определения логарифмической функции

Логарифмическая функция выражается как: y=log nk

Где значение n, имеет значение больше нуля и не менее единицы. Область определения логарифма и логарифмической функции — это  множество положительных значений и действительных чисел.

Рассмотрим на примере, характер решения задачи данной функции.

Пример №1

y=ln x, определить область определения натурального логарифма. D(y)=(0;+).

На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.

\

Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.

Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.

Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.

Ответ: множество всех действительных чисел, это и есть область значений функции ln.

Неявные функции. Параметрически заданные функции.

Пусть Е — множество точек \(M(x,y)\) плоскости \(Oxy\). Если каждой точке \(M\in E\) поставлено в соответствие по некоторому правилу (закону) число z, то говорят, что на множестве E задана числовая функция от переменных \(x\) и \(y\), и пишут \(z=f(x,y),\;(x,y)\in E\).

Например, объем конуса \(v\) есть функция от переменных r и h, где r — радиус основания, h — высота конуса. Эта функция задается формулой \(v=\displaystyle \frac{1}{3}\pi r^{2}h\).

Аналогично вводится понятие функции от трех и большего числа переменных.

Пусть функция \(F(x,y)\) определена на некотором множестве точек плоскости. Рассмотрим уравнение
$$
F(x,y)=0.\label{ref9}
$$

Рис. 9.12

Графиком уравнения \eqref{ref9} в прямоугольной системе координат называют множество всех точек плоскости, координаты которых удовлетворяют этому уравнению. Например, графиком уравнения
$$
x^{2}+y^{2}-1=0\label{ref10}
$$
является единичная окружность (рис. 9.12).

Естественной является постановка вопроса о том, можно ли уравнение \eqref{ref9} однозначно разрешить относительно \(y\), то есть найти единственную функцию \(y=f(x)\) такую, что \(F(x,f(x))=0\), где \(x\) принимает значения из некоторого промежутка.

Обратимся к уравнению \eqref{ref10}. Если \(|x|>1\), то не существует значений \(y\) таких, что пара чисел \((x,y)\) удовлетворяет уравнению \eqref{ref10}. Если \(|x|\leq 1\), то, решая это уравнение относительно y, получаем
$$
y=\pm\sqrt{1-x^{2}}.\label{ref11}
$$

Таким образом, если \(|x|\;<1\), то из уравнения \eqref{ref10} \(y\) выражается через \(х\) неоднозначно: каждому значению \(x\) соответствуют два различных значения \(y\), а именно \(y_{1}=-\sqrt{1-x^{2}}\quad y_{2}=\sqrt{1-x^{2}}\quad (y_{1}=y_{2}\) при \(x=-1\;x=1)\).

Отсюда следует, что всякая функция \(y=f(x)\), которая в точке \(x\in\) принимает либо значение \(y_{1}\), либо значение \(y_{2}\), удовлетворяет уравнению \eqref{ref10}, то есть
$$
x^{2}+f^{2}(x)-1=0,\quad x\in.\nonumber
$$

Например, функция \(y=f(x)\), принимающая значение \(y_1\) при \(x\in\), удовлетворяет уравнению \eqref{ref10}. Меняя \(\alpha\), можно получить бесконечное множество функций, удовлетворяющих на отрезке \(\) уравнению \eqref{ref10}.

Будем теперь рассматривать уравнение \eqref{ref10} в прямоугольнике
$$
K_{1}=\{(x,y):-1\leq x\leq 1,\;0\leq y\leq 1\}.\nonumber
$$

В этом случае существует единственная функция \(y=y_{1}=\sqrt{1-x^{2}},\;-1\leq x\leq 1\), удовлетворяющая уравнению \eqref{ref10} и такая, что \(y\in\). Эту функцию называют неявной функцией, определяемой уравнением \eqref{ref10} в прямоугольнике \(K_1\).

Аналогично в прямоугольнике \(K_{1}=\{(x,y):-1\leq x\leq 1,\;-1\leq y\leq 0\}\) неявная функция, определяемая уравнением \eqref{ref10}, задается формулой \(y=y_{2}=-\sqrt{1-x^{2}},\;-1\leq x\leq 1\).

Вернемся к уравнению \eqref{ref9}. Пусть прямоугольник \(K=\{(x,y):|x-x_{0}|\leq a,\;|y-у_0|\leq b\) содержится в области определения функции \(F(х,у)\), и пусть \(F(х_0,y_0)=0\). Если на отрезке \(\Delta=\lceil x_{0}-a,x_{0}+a\rceil\) существует единственная функция \(y=f(x)\) такая, что \(f(x)\in\lceil y_0-b,y_0+b\rceil\) и
$$
F(x,f(x))=0,\quad x\in\Delta,\nonumber
$$
то говорят, что уравнение \eqref{ref9} определяет в прямоугольнике \(K\) переменную y как неявную функцию переменной \(x\).

Достаточные условия существования неявной функции и другие вопросы, связанные с неявными функциями, рассматриваются далее в параграфе 28.

Функция одной переменной может быть задана не только в явном виде \(y=f(x)\) или неявно уравнением \(F(х,у)=0\), но также параметрически. Этот способ задания состоит в следующем.

Пусть функции \(x=\varphi(t)\) и \(\varphi(t)\) определены на некотором множестве \(E\), и пусть \(E_1\) — множество значений функции \(\varphi\). Предположим, что функция \(\varphi\) обратима на множестве \(E\), и пусть \(t=\varphi^{-1}(x)\) — обратная к ней функция. Тогда на множестве \(E_1\) определена сложная функция \(y=\psi(\varphi^{-1}(x))=f(x)\), которую называют параметрически заданной формулами (уравнениями) \(х=\varphi(t),\quad y=\psi(t)\).

Например, уравнениях \(x=\cos t,\;y=\sin t\), где \(t\in\left \), определяют параметрически заданную функцию \(y=f(x)\). В данном случае \(t=\arccos x,\;y=\sin(\arccos x)=\sqrt{1-x^{2}}\).

Что такое ОДЗ?

ОДЗ – это аббревиатура от «область допустимых значений», используется в математике для обозначения множества значений переменной или функции, которые являются корректными для данного выражения. ОДЗ может быть определена как множество всех возможных значений переменной, которые лежат в определенном диапазоне.

ОДЗ может быть определена для различных математических функций, включая логарифмические, тригонометрические, алгебраические, и многие другие. Для определения ОДЗ нужно учитывать все ограничения функции и знать, какие значения могут привести к появлению некорректных результатов.

Важно помнить, что ОДЗ может быть изменена, если у нас нет достаточной информации о функции, которую мы рассматриваем. Например, если мы не знаем, что функция имеет ограничение на определенный диапазон значений, мы можем рассматривать ОДЗ, которое не является истинным

Способы задания функции.

Числовые функции чаще всего задаются при помощи формул. Такой способ задания называют аналитическим. Например, функции \(y=x^2, \ y=|x|^{3/2}, \ y=\sin^3{3x}\) заданы на множестве \(\mathbb{R}\) аналитически.

Если числовая функция f задана формулой и не указана область ее определения \(D(f)\) , то принято считать, что \(D(f)\) — множество всех тех значений аргумента, при которых эта формула имеет смысл, и результатом каждой операции, указанной в формуле, является вещественное число. Например, если \(f(x)=\sqrt{9-x^2}\), то \(D(f)=\), а если \(f(x)=\sqrt{\operatorname{lg} \sin{x}}\), то \(D(f)\) — множество корней уравнения \(\sin x=1\) то есть множество чисел \(x_{k}=\pi/2.+2\pi k\), где \(k\in Z\).

Следует отметить, что функция может быть задана различными формулами на разных промежутках. Например, функция
$$
f(x)=\left\{\begin{array}{l}-x,\quad если\;x\;<\;0,\\x^{2},\quad если\;0\leq x\leq1,\\2-\sqrt{x},\quad если\;x>1,\end{array}\right.\nonumber
$$
задана аналитическим способом на \(\mathbb{R}\) с помощью трех различных формул.

Иногда функциональная зависимость описывается с помощью таблицы, содержащей лишь некоторые значения аргумента и соответствующие значения функции. Для значений аргумента, не содержащихся в таблице, значения функции обычно находят приближенно.

На практике часто соответствие между значениями аргумента и значениями функции задается с помощью рисунка. Например, в медицине при изучении работы сердца получают электрокардиограммы — кривые, отражающие изменение с течением времени электрических импульсов в мышце сердца. В практике физических измерений функциональная зависимость часто задается с помощью эскиза графика, снимаемого, например, с экрана осциллографа.

Определения области значения функции x

На примерах рассмотрим, как определить области значений функции.

Первоначально, необходимо определить значения непрерывной функции y=f(x).

Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.

Пример №1

Необходимо вычислить область значений уравнения

y = x4-5×3+6×2 на отрезке .

Для решения задачи необходимо произвести следующие действия:

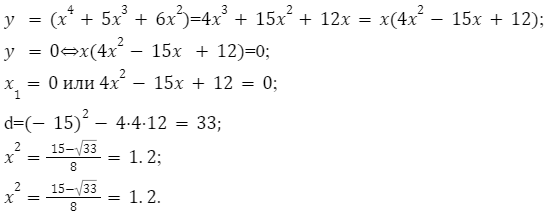
Следующим шагом будет определение значений функции в конечной и начальной точках.

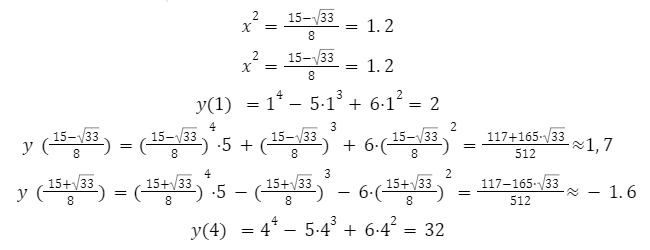
Ответ: \.

Пример №2

Необходимо вычислить область значений уравнения

y = x4-7×3+5×2на отрезке

Для решения задачи необходимо произвести следующие действия:

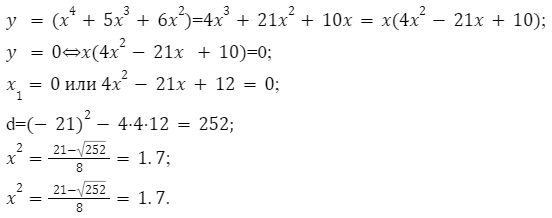
Следующим шагом будет определение значений функции в конечной и начальной точках.

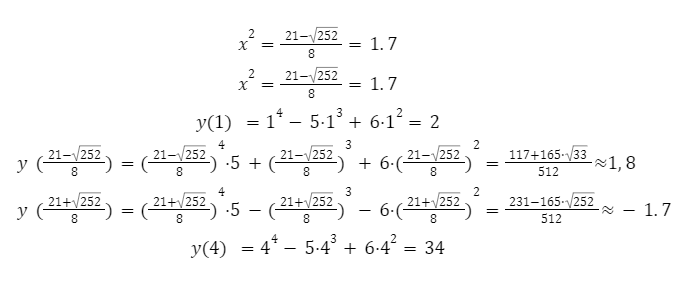
Ответ: \.

Пример №3

На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.

Для этого, первоначально вычислим:

• наименьшее и наибольшее значение;
• определим промежуток возрастания и убывания функции;
• односторонние пределы;
• предел бесконечности.

Решение:

Для решения возьмем функцию \ и вычислим область значений на промежутке (-2;2).

Находим наименьшее и наибольшее значение функции на заданном отрезке.

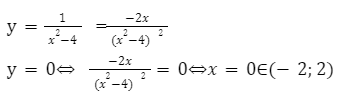
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.

А именно: \;

\ — будет являться наибольшим значение заданной функции.

Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).

В алгебре иными словами эти значения называют односторонними пределами.

Решение выглядит следующим образом.

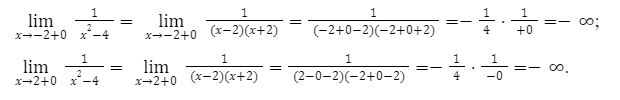
В конечном итоге мы получаем, что в пределах от -2 до , функции будут возрастать от -∞ до \. Если аргумент меняется, от до то наоборот будет убывать к -∞.

Следовательно, необходимое множество значений будет на интервале -∞ до \.

Ответ: \.

Пример №4

Для решения возьмем функцию \ и вычислим область значений на промежутке (-2;3).

Находим наименьшее и наибольшее значение функции на заданном отрезке.

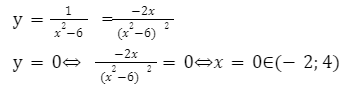
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.

А именно: \;

\ — будет являться наибольшим значение заданной функции.

Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+4).

В алгебре иными словами эти значения называют односторонними пределами.

Решение выглядит следующим образом.

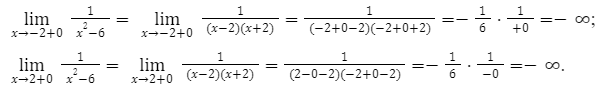
В конечном итоге мы получаем, что в пределах от -2 до , функции будут возрастать от -∞ до \. Если аргумент меняется, от до то наоборот будет убывать к -∞.

Следовательно, необходимое множество значений будет на интервале -∞ до\.

Ответ: (-∞ \).