Основные сведения об области определения логарифмической функции

Логарифмическая функция, ее свойства и график

При рассмотрении какого-либо логарифмируемого числа в качестве переменной получается логарифмическая функция, имеющая следующий вид: \(y=\log _{a}x\).

Областью определения данной функции являются такие значения, которые соответствуют интервалу:

\(a>0;\ a\neq 1;x>0.\)

Область значений логарифмической функции определена таким образом:

\(E(y) = (-\infty ;+\infty).\)

На графике логарифмическая функция имеет вид кривой, которую часто называют логарифмикой. Согласно формуле, с помощью которой осуществляют замену основания логарифма, сделаем вывод о том, что:

• графики логарифмических функций, имеющих разные основания, больше единицы, различаются по масштабу относительно оси y;
• графики логарифмических функций для оснований, меньших, чем единица, представляют собой их зеркальное отражение по отношению к горизонтальной оси.

Изобразим графики логарифмических функций:

Согласно определению, логарифмическая функция является обратной для показательной функции \(y=a^{x}\). По этой причине графические изображения данных функций будут симметричными по отношению к биссектрисе первого и третьего квадрантов. Обе эти функции трансцендентны.

Заметим следующие особенности логарифмической функции:

• строгое возрастание графика, если a>1;
• строгое убывание графика, если 0<a<1.

Графически изображенная логарифмическая функция в любом случае будет пересекать точку с координатами (1;0). Функция не прерывается и дифференцируется без ограничений на любом участке в рамках собственной области определений.

Ось ординат при x=0 представляет собой вертикальную асимптоту, так как:

• \(\lim _{x\to 0+0}\log _{a}x=-\infty\) при a>1;
• \(\lim _{x\to 0+0}\log _{a}x=+\infty\) при 0<a<1.

Производную логарифмической функции вычисляют по формуле:

\({\frac {d}{dx}}\log _{a}x={\frac {1}{x\cdot \ln a}}\)

Логарифмическая функция представляет собой непрерывное решение, которое считают единственно верным, для следующего функционального уравнения:

\(f(xy)=f(x)+f(y).\)

Свойства функции \(y={{log}_a x\ }\), при a >1:

1. Областью определения данной функции является интервал \((0,+\infty )\).
2. Значения функции определяются, как множество действительных чисел.
3. Данную функцию нельзя отнести к типу четных или нечетных.
4. График пересекает оси координат. С осью Oy точки пересечения отсутствуют. Если \(y=0\), \({{log}_a x\ }=0,\ x=1\). Функция пересекается с осью Ox в точке (1,0).
5. Функция является положительной, если \(x\in (1,+\infty )\). Функция является отрицательной в том случае, когда \(x\in (0,1)\).
6. \(y’=\frac{1}{xlna}\).
7. Точки минимума и максимума: \(\frac{1}{xlna}=0\), при этом корни отсутствуют, то есть максимальные и минимальные точки также отсутствуют.
8. Функция является возрастающей на всей области определения.
9. \(y^{»}=-\frac{1}{x^2lna}\).
10. Промежутки выпуклости и вогнутости: \(-\frac{1}{x^2lna}\). Функция является выпуклой на всей области, в которой определяется.
11. \({\mathop{lim}_{x\to 0} y\ }=-\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=+\infty.\)

Рассмотрим свойства функции \(y={{log}_a x\ }, 0 < a < 1:\)

1. Функция определяется на интервале \((0,+\infty).\)
2. Значениями функции являются все числа из множества действительных.
3. Данную функцию нельзя отнести к типу четных или нечетных.
4. Отсутствуют пересечения графика с осью Oy. Если \(y=0, {{log}_a x\ }=0,\ x=1\).Функция пересекает ось Ox в точке с координатами: (1,0).
5. Функция является положительной, если \(x\in (0,1)\). Функция является отрицательной в том случае, когда \(x\in (1,+\infty).\)
6. \(y’=\frac{1}{xlna}.\)
7. Точки минимума и максимума: \( \frac{1}{xlna}=0\); в этом случае корни отсутствуют — значит, отсутствуют максимальные и минимальные точки.
8. Функция является убывающей на всей области, в которой она определена.
9. \(y^{»}=-\frac{1}{x^2lna}\).
10. Промежутки выпуклости и вогнутости: \( -\frac{1}{x^2lna}>0\). Функция является вогнутой на всей области, в которой она определена.
11. \(\mathop{lim}_{x\to 0} y\ =+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty\).

Постоянная функция.

Постоянная функция задается на множестве всех действительных чисел формулой , где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.

Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5, y=-2 и , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.

Свойства постоянной функции.

• Область определения: все множество действительных чисел.
• Постоянная функция является четной.
• Область значений: множество, состоящее из единственного числа С.
• Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
• Говорить о выпуклости и вогнутости постоянной не имеет смысла.
• Асимптот нет.
• Функция проходит через точку (0,C) координатной плоскости.

Примеры исследования и построения логарифмических функций

Пример 1

Исследовать и построить график функции $y=2-{{log}_2 x\ }$

1. Область определения — интервал $(0,+\infty )$;

2. Область значения — все действительные числа;

3. Функция не является ни четной, ни нечетной.

4. Точки пересечения с осями координат:

   С осью $Oy$ пересечений нет.

   При $y=0$, $2-{{log}_2 x\ }=0,\ x=4.$ Пересечение с осью $Ox$: (4,0).

5. Функция положительна, при $x\in (0,4)$ и отрицательна, при $x\in (4,+\infty )$

6. $y’=-\frac{1}{xln2}$;

7. Точки минимума и максимума:

   \

   Точек максимума и минимума нет.

8. Функция убывает на всей области определения;

9. $y^{»}=\frac{1}{x^2ln2}$;

10. Промежутки выпуклости и вогнутости:

    \

    Функция вогнута на всей области определения;

11. ${\mathop{lim}_{x\to 0} y\ }=+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty ,\ $;

12. График функции:

Рисунок 3.

Область определения функции с корнем

По определению, логарифмическая функция имеет вид:

\(y=\log _{a} x,\; a,\, x>0,\; a\ne 1.\)

Областью определения функции \(D\left(y\right)\) является такое множество, на котором задана функция \(y=f\left(x\right)\), при этом каждая точка рассматриваемого множества соответствует определенному значению функции.

В случае логарифмической функции, в том числе, с корнем квадратным, дробью со знаменателем, отличным от нуля, область определения соответствует какому-либо числу со знаком плюс из множества действительных чисел:

\(D\left(\log _{a} x\right):x\in \left(0;\; +\infty \right)\)

Рассмотрим несколько примеров логарифмических функций, чтобы узнать область их определений:

\(y=\log _{ \frac{2}{3} } x;\)

\(y=\log _{ \sqrt{5}} x;\)

\(y=\log _{7} x.\)

Областью определения записанных логарифмических функций, в том числе, с корнем, является интервал \((0, +\infty)\).

Попробуем решить задачу. Здесь требуется искать область определения в случае функции:

\(f(x)=\frac{1}{ln(x+3)}\)

Условия следующие:

х + 3 > 0

\(x + 3 \neq 1\)

Тогда:

х > -3

\(x \neq -2\)

Тогда область определения соответствует следующим значениям:

\(D(f) = (-3, -2) \cup (-2, +\infty).\)

Свойства логарифма

Область определения, множество значений, возрастание, убывание

Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.

Область определения
Область значений	— ∞	— ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y =	x = 1	x = 1
Точки пересечения с осью ординат, x =	нет	нет
	+ ∞	— ∞
	— ∞	+ ∞

Частные значения

Логарифм по основанию 10 называется десятичным логарифмом
и обозначается так: Логарифм по основанию e
называется натуральным логарифмом
:

Основные формулы логарифмов

Свойства логарифма, вытекающие из определения обратной функции:

Формула замены основания

Логарифмирование
— это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.

Потенцирование
— это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.

Доказательство основных формул логарифмов

Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.

Рассмотрим свойство показательной функции.
Тогда.
Применим свойство показательной функции:
.

Докажем формулу замены основания.
;
.
Полагая c = b
,
имеем:

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:e
= 2,718281828459…

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x

Таким образом, ln e
= 1 ; ln e
2 = 2 ; ln e
16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

1.8. Формула возведения дроби в степень.

E = lim(1+1/N), при N → ∞.

С точностью 17 знаков число e равно 2.71828182845904512.

6. Логарифм.

6.1. Определение функции логарифм

Y = Log b (x).

Логарифм показывает в какую степень надо возвести число — основание логарифма (b), чтобы
получить заданное число (X). Функция логарифм определена для X больше нуля.

Например: Log 10 (100) = 2.

Y = Log 10 (x) .

Обозначается Log(x): Log(x) = Log 10 (x).

Пример использования десятичного логарифма — децибел .

Y = Log 2 (x).

Обозначается Lg(x): Lg(x) = Log 2 (X)

6.5. Натуральный логарифм

Y = Log e (x) .

Обозначается Ln(x): Ln(x) = Log e (X)
Натуральный логарифм — обратная функция к экспоненциальной функции exp (X).

Пример:

Log 2 (8) = Log 10 (8)/Log 10 (2) =
0.903089986991943552 / 0.301029995663981184 = 3

7. Формулы полезные в жизни

Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича .

Разрешается использовать материалы сайта при условии установки активной ссылки на источник.

Логарифмом
данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием
логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (10 2 = 100). Если n
– заданное число, b
– основание и l
– логарифм, то b l = n
. Число n
также называется антилогарифмом по основанию b
числа l
. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений log b n
= l
и antilog b l
= n
.

Основные свойства логарифмов:

Любое положительное число, кроме единицы, может служить основанием логарифмов, но, к сожалению, оказывается, что если b
и n
– рациональные числа, то в редких случаях найдется такое рациональное число l
, что b l = n
. Однако можно определить иррациональное число l
, например, такое, что 10 l
= 2; это иррациональное число l
можно с любой требуемой точностью приблизить рациональными числами. Оказывается, что в приведенном примере l
примерно равно 0,3010, и это приближенное значение логарифма по основанию 10 числа 2 можно найти в четырехзначных таблицах десятичных логарифмов. Логарифмы по основанию 10 (или десятичные логарифмы) столь часто используются при вычислениях, что их называют обычными
логарифмами и записывают в виде log2 = 0,3010 или lg2 = 0,3010, опуская явное указание основания логарифма. Логарифмы по основанию e
, трансцендентному числу, приближенно равному 2,71828, называются натуральными
логарифмами. Они встречаются преимущественно в работах по математическому анализу и его приложениям к различным наукам. Натуральные логарифмы также записывают, не указывая явно основание, но используя специальное обозначение ln: например, ln2 = 0,6931, т.к. e
0,6931 = 2.

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

.

Тогда любое число, либо переменную у можно представить в виде:

,

где х любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

.

Воспользуемся свойством  (только вместо с у нас выражение):

Отсюда получаем универсальную формулу:

.

В частности, если z=e, то тогда:

.

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1. Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если , то  , получаем:

.

Задача 2. Решите уравнение (5 + 3 * ln (x 3)) = 3.

Решение: Используя определение логарифма: если , то  , получаем:

.

Тогда:

.

.

Еще раз применим определение логарифма:

.

Таким образом:

.

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение .

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

.

Перед нами квадратное уравнение. Найдем его дискриминант:

.

Первый корень уравнения:

.

Второй корень уравнения:

.

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

.

Используя определение логарифма: если  , то , получаем оба корня:

.

Вспомним, что область определения: . Оба корня больше нуля, так что оба решения верны и подходят.

Внимание! Когда в логарифмических уравнениях у вас получается два корня или больше, не забывайте про область определения. Аргумент, стоящий под логарифмом никогда не может быть меньше нуля

Если одно из решений делает выражение под логарифмом меньше либо равным нулю такой корень вам не подходит, исключите его.

Логарифмическая функция, ее свойства и график

Для начала вспомним, что же вообще такое логарифм.

Определение 1

Логарифмом числа $bin R$ по основанию $a$ ($a>0, a
e 1$) называется число $c$, в которое нужно возвести число $a$, чтобы получить число $b$.

Рассмотрим показательную функцию $fleft(x
ight)=a^x$, где $a >1$. Эта функция возрастает, непрерывна и отображает действительную ось на интервал $(0,+infty )$.

Тогда, по теореме о существовании обратной непрерывной функции, у нее в множестве $Y=(0,+infty )$ существует обратная функция $x=f^{-1}(y)$, которая также непрерывна и возрастает в $Y$ и отображает интервал $(0,+infty )$ на всю действительную ось.

Эту обратную функцию называют логарифмической функцией по основанию $a (a >1)$ и обозначается $y={{log}_a x }$.

Теперь рассмотрим показательную функцию $fleft(x
ight)=a^x$, где $0

Таким образом, мы определили логарифмическую функцию при всех возможных значениях основания $a$. Рассмотрим далее два этих случая отдельно.

Функция $y={{log}_a x }, a >1$

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Рассмотрим свойства данной функции.

1. Область определения — интервал $(0,+infty )$;

2. Область значения — все действительные числа;

3. Функция не является ни четной, ни нечетной.

4. Точки пересечения с осями координат:

   С осью $Oy$ пересечений нет.

   При $y=0$, ${{log}_a x }=0, x=1.$ Пересечение с осью $Ox$: (1,0).

5. Функция положительна, при $xin (1,+infty )$ и отрицательна, при $xin (0,1)$

6. $y’=frac{1}{xlna}$;

7. Точки минимума и максимума:

   Точек максимума и минимума нет.

8. Функция возрастает на всей области определения;

9. $y^{»}=-frac{1}{x^2lna}$;

10. Промежутки выпуклости и вогнутости:

    [-frac{1}{x^2lna}Функция выпукла на всей области определения;

11. ${mathop{lim}_{x o 0} y }=-infty , {mathop{lim}_{x o +infty } y }=+infty , $;

12. График функции (Рис. 1).

Рисунок 1. График функции $y={{log}_a x }, a >1$

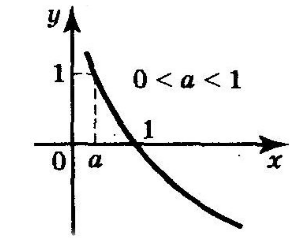
Функция $y={{log}_a x }, 0

Рассмотрим свойства данной функции.

1. Область определения — интервал $(0,+infty )$;

2. Область значения — все действительные числа;

3. Функция не является ни четной, ни нечетной.

4. Точки пересечения с осями координат:

   С осью $Oy$ пересечений нет.

   При $y=0$, ${{log}_a x }=0, x=1.$ Пересечение с осью $Ox$: (1,0).

5. Функция положительна, при $xin (0,1)$ и отрицательна, при $xin (1,+infty )$

6. $y’=frac{1}{xlna}$;

7. Точки минимума и максимума:

   Точек максимума и минимума нет.

8. Функция убывает на всей области определения;

9. $y^{»}=-frac{1}{x^2lna}$;

10. Промежутки выпуклости и вогнутости:

    Функция вогнута на всей области определения;

11. ${mathop{lim}_{x o 0} y }=+infty , {mathop{lim}_{x o +infty } y }=-infty , $;

12. График функции (Рис. 2).

Примеры исследования и построения логарифмических функций

Пример 1

Исследовать и построить график функции $y=2-{{log}_2 x }$

1. Область определения — интервал $(0,+infty )$;

2. Область значения — все действительные числа;

3. Функция не является ни четной, ни нечетной.

4. Точки пересечения с осями координат:

   С осью $Oy$ пересечений нет.

   При $y=0$, $2-{{log}_2 x }=0, x=4.$ Пересечение с осью $Ox$: (4,0).

5. Функция положительна, при $xin (0,4)$ и отрицательна, при $xin (4,+infty )$

6. $y’=-frac{1}{xln2}$;

7. Точки минимума и максимума:

   Точек максимума и минимума нет.

8. Функция убывает на всей области определения;

9. $y^{»}=frac{1}{x^2ln2}$;

10. Промежутки выпуклости и вогнутости:

    Функция вогнута на всей области определения;

11. ${mathop{lim}_{x o 0} y }=+infty , {mathop{lim}_{x o +infty } y }=-infty , $;

12. График функции:

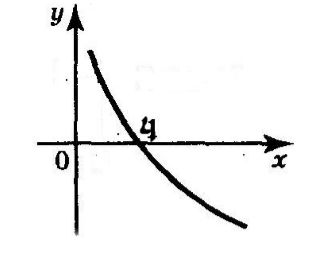
Рисунок 3.

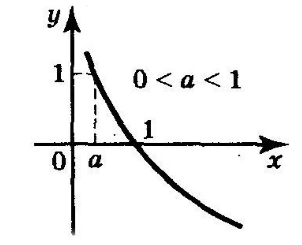
Функция $y={{log}_a x\ }, \ 0

Рассмотрим свойства данной функции.

1. Область определения — интервал $(0,+\infty )$;

2. Область значения — все действительные числа;

3. Функция не является ни четной, ни нечетной.

4. Точки пересечения с осями координат:

   С осью $Oy$ пересечений нет.

   При $y=0$, ${{log}_a x\ }=0,\ x=1.$ Пересечение с осью $Ox$: (1,0).

   

   

   

   

   

   

   

   

   

   

5. Функция положительна, при $x\in (0,1)$ и отрицательна, при $x\in (1,+\infty )$

6. $y’=\frac{1}{xlna}$;

7. Точки минимума и максимума:

   \

   Точек максимума и минимума нет.

8. Функция убывает на всей области определения;

9. $y^{»}=-\frac{1}{x^2lna}$;

10. Промежутки выпуклости и вогнутости:

    \

    Функция вогнута на всей области определения;

11. ${\mathop{lim}_{x\to 0} y\ }=+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty ,\ $;

12. График функции (Рис. 2).

Логарифмическая функция в природе и науке

Логарифм – это не просто инструмент для выполнения сложных операций. Например, в теории вероятностей существуют логарифмическое и логнормальное (от слов «логарифм» и «нормальное») распределение случайных величин, которые используются в генетике и физике. Так, размеры астероидов в Солнечной системе описываются логарифмическим распределением, а размеры градин во время града – логнормальным.

В компьютерной технике многие величин можно вычислить с использованием логарифмов. Например, ясно, что чем больше телефонных номеров находится в базе данных, тем дольше компьютер будет искать требуемый необходимый номер в ней. Зависимость времени поиска от количества номеров в базе данных описывается логарифмической функцией.

Огромное значение логарифмы имеют в астрономии. Так, яркость звезд на небе характеризуется таким параметром, как «видимая звездная величина». Однако в физике для оценки яркости света используют величину «освещенность», измеряемую в люксах. Зависимость между освещенностью звезд и их видимой величиной также является логарифмической.

Используются логарифмы и в термодинамике для вычисления такой характеристики систем, как энтропия. При расчете количества топлива, необходимого ракете для набора определенной скорости, используется формула Циолковского, содержащая натуральный логарифм:

В биологии давно замечено, что зависимость человеческих ощущений от силы воздействующих на них факторов окружающей среды носит логарифмический характер. В связи с этим для измерения громкости звуков используется специальная шкала децибелов, которая является логарифмической.

В строении ряда организмов можно обнаружить логарифмические кривые. Классическим примером является форма некоторых ракушек.