Способ вычисления натурального логарифма

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Численное значение

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

y
x
x
x

Для ln(x
), где x
> 1, чем ближе значение x
к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:

где M
обозначает арифметико-геометрическое среднее 1 и 4/s, и

m
выбрано так, что p
знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M
(n
) ln n
). Здесь n
— число цифр точности, для которой натуральный логарифм должен быть оценен, а M
(n
) — вычислительная сложность умножения двух n
-значных чисел.

Ввод функций:

Функции вводятся с использованием маленьких латинских букв: sin ; cos ; tan ; log

ВНИМАНИЕ! Аргумент функции всегда берется в скобки () , например: sin( 4 ) ; cos( x ) ; log( 4 + y ). Запись типа: sin 4 ; cos x ; log 4 + y – недопустима. Правильная запись: sin( 4 ) ; cos( x ) ; log( 4 + y )

Если необходимо возвести функцию в степень, например: синус x и все это в квадрате, это записывается вот так: (sin( x )) ^ 2. Если необходимо возвести в квадрат аргумент, а не функцию (т.е синус от x ^ 2 ), тогда это выглядит вот так: sin( x ^ 2). Запись типа: sin ^ 2 x – недопустима

Правильная запись: sin( 4 ) ; cos( x ) ; log( 4 + y ) . Если необходимо возвести функцию в степень, например: синус x и все это в квадрате, это записывается вот так: (sin( x )) ^ 2 . Если необходимо возвести в квадрат аргумент, а не функцию (т.е синус от x ^ 2 ), тогда это выглядит вот так: sin( x ^ 2) . Запись типа: sin ^ 2 x – недопустима .

Источник статьи: http://mathforyou.net/online/input/simple/

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Натуральные логарифмы.

Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов. Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли. Натуральные логарифмы чисел 5,432; 54,32 и 543,2 равны, соответственно, 1,6923; 3,9949 и 6,2975. Взаимосвязь между этими логарифмами станет очевидной, если рассмотреть разности между ними: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; последнее число есть не что иное, как натуральный логарифм числа 10 (пишется так: ln10); log543,2 – log5,432 = 4,6052; последнее число равно 2ln10. Но 543,2 = 10ґ54,32 = 10 2 ґ5,432. Таким образом, по натуральному логарифму данного числа a
можно найти натуральные логарифмы чисел, равные произведениям числа a
на любые степени n
числа 10, если к lna
прибавлять ln10, умноженный на n
, т.е. ln(a
ґ10 n
) = lna
+ n
ln10 = lna
+ 2,3026n
. Например, ln0,005432 = ln(5,432ґ10 –3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще говорят об экспоненциальной функции или об экспоненте. Если x
= lny
, то y
= e x
, и y
называется экспонентой от x
(для удобства типографского набора часто пишут y
= exp x
). Экспонента играет роль антилогарифма числа x
.

С помощью таблиц десятичных и натуральных логарифмов можно составить таблицы логарифмов по любому основанию, отличному от 10 и e
. Если log b a
= x
, то b x
= a
, и, следовательно, log c b x
= log c a
или x
log c b
= log c a
, или x
= log c a
/log c b
= log b a
. Следовательно, с помощью этой формулы обращения из таблицы логарифмов по основанию c
можно построить таблицы логарифмов по любому другому основанию b
. Множитель 1/log c b
называется модулем перехода
от основания c
к основанию b
. Ничто не мешает, например, пользуясь формулой обращения, или перехода от одной системы логарифмов к другой, найти натуральные логарифмы по таблице обычных логарифмов или совершить обратный переход. Например, log105,432 = log e
5,432/log e
10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Число 0,4343, на которое нужно умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

4. Дифференцирование функции y=ln x

Ло­га­риф­ми­че­скую функ­цию с на­ту­раль­ным ос­но­ва­ни­ем можно диф­фе­рен­ци­ро­вать. Да­вай­те на­учим­ся это де­лать.

Для этого до­ка­жем фор­му­лу .

До­ка­за­тель­ство.

Мы знаем, что ;

Зна­чит, про­из­вод­ная от слож­ной функ­ции ;

Также знаем ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство:

;

Про­диф­фе­рен­ци­ру­ем тож­де­ство :

1=

1=

Вы­ра­зим :

.

Фор­му­ла до­ка­за­на. Те­перь диф­фе­рен­ци­ро­вать ло­га­риф­ми­че­ские функ­ции с на­ту­раль­ным ос­но­ва­ни­ем мы можем.

В итоге имеем две важ­ные фор­му­лы:

;

Зна­чит, мы умеем ре­шать любые ти­по­вые за­да­чи на про­из­вод­ную ло­га­риф­ми­че­ской функ­ции с ос­но­ва­ни­ем .

Примечания

1. ↑ Mortimer, Robert G. Mathematics for physical chemistry (неопр.). — 3rd. — Academic Press, 2005. — С. 9. — ISBN 0-125-08347-5., Extract of page 9
2. ↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
3. ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
4. ↑ Корн Г., Корн Т. Справочник по математике, 1973, с. 34.
5. ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
6. ↑ 1 2 3 Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
7. ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 159-160.
8. ↑ Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x) (англ.) // Journal of Information Processing. — 1982. — Vol. 5, iss. 4. — P. 247—250.
9. ↑ Ahrendt, Timm. Fast computations of the exponential function. Lecture notes in computer science (неопр.). — 1999. — Т. 1564. — С. 302—312. — doi:10.1007/3-540-49116-3_28.
10. ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 164.
11. ↑ Рудио Ф. О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). — Изд. 3-е. — М.—Л.: ОГИЗ, 1936. — С. 89. — 237 с. — (Классики естествознания).
12. ↑ Cajori, Florian. A History of Mathematics, 5th ed (неопр.). — AMS Bookstore, 1991. — С. 152. — ISBN 0821821024.
13. ↑ Flashman, Martin. Estimating Integrals using Polynomials (неопр.). Дата обращения: 30 июня 2011. Архивировано 11 февраля 2012 года.
14. ↑ J J O’Connor and E F Robertson. The number e (неопр.). The MacTutor History of Mathematics archive (сентябрь 2001). Дата обращения: 30 июня 2011. Архивировано 11 февраля 2012 года.
15. ↑ 1 2 История математики, том III, 1972, с. 325-328..
16. ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231..
17. ↑ 1 2 Корн Г., Корн Т. Справочник по математике, 1973, с. 623..
18. ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 45-46, 99-100..
19. ↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
20. ↑ Weisstein, Eric W. Log-Series Distribution (англ.). MathWorld. Дата обращения: 26 апреля 2012.
21. ↑ Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
22. ↑ Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
23. ↑ Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
24. ↑ Головин С. Ю. ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога (неопр.). Дата обращения: 17 апреля 2012.
25. ↑ Ирина Алдошина. Основы психоакустики // Звукорежиссёр. — 1999. — Вып. 6. Архивировано 24 апреля 2012 года.
26. ↑ Закон Фиттса // Психологическая энциклопедия (неопр.) (недоступная ссылка). Дата обращения: 17 апреля 2012. Архивировано 27 мая 2012 года.
27. ↑ Welford, A. T. Fundamentals of skill. — London: Methuen, 1968. — P. 61. — ISBN 978-0-416-03000-6.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Продолжаем изучать логарифмы. В этой статье мы поговорим про вычисление логарифмов
, этот процесс называют логарифмированием
. Сначала мы разберемся с вычислением логарифмов по определению. Дальше рассмотрим, как находятся значения логарифмов с использованием их свойств. После этого остановимся на вычислении логарифмов через изначально заданные значения других логарифмов. Наконец, научимся использовать таблицы логарифмов. Вся теория снабжена примерами с подробными решениями.

Навигация по странице.

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

Тогда любое число, либо переменную у можно представить в виде:

где х — любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

Воспользуемся свойством (только вместо «с» у нас выражение):

Отсюда получаем универсальную формулу:

.

В частности, если z=e, то тогда:

.

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1
. Необходимо решить уравнение ln x = 3.

Решение:
Используя определение логарифма: если , то , получаем:

Задача 2
. Решите уравнение (5 + 3 * ln (x — 3)) = 3.

Решение: Используя определение логарифма: если , то , получаем:

.

Еще раз применим определение логарифма:

.

Таким образом:

.

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3.
Решите уравнение .

Решение:
Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

.

Перед нами квадратное уравнение. Найдем его дискриминант:

Первый корень уравнения:

.

Второй корень уравнения:

.

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике
нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

Доказательство основного свойства натурального логарифма

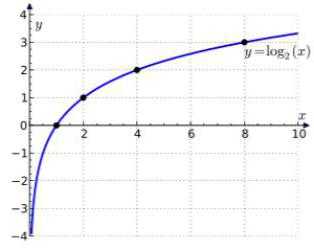
График натурального логарифма

Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.

Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:

Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:

Для удобства мы можем взять пять опорных точек:

;

;

.

;

.

Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.

Построив по точкам график, получаем приблизительный график:

Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.

Внимание!
В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма

Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .

Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Что такое натуральный логарифм

логарифмические функции

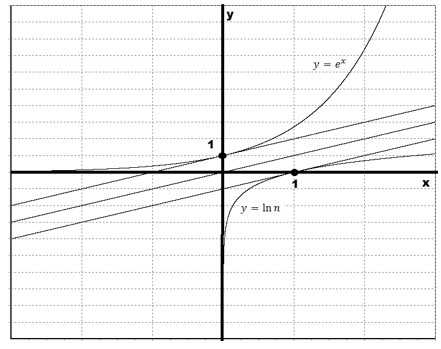
Стоит заметить угол наклона касательной к графику функции $y=e^x$ в точке (0;1) равен 45&deg. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45&deg. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:

Свойства функции $y=\ln{x}$

Наибольшего значениянаименьшего значения

В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции
. Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.

Пример.

Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять.
$y»=(\ln{(2x-7)})»=\frac{2}{(2x-7)}$.
Вычислим значение производной в требуемой точке: $y»(4)=\frac{2}{(2*4-7)}=2$.
Ответ: 2.

Пример.
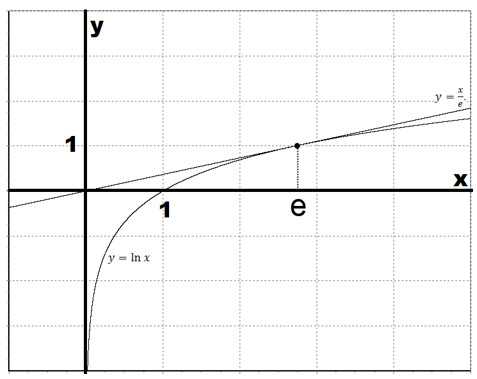
Провести касательную к графику функции $y=ln{x}$ в точке $х=е$.
Решение.
Уравнение касательной к графику функции, в точке $х=а$, мы хорошо помним.
$y=f(a)+f»(a)(x-a)$.
Последовательно вычислим требуемые значения.
$a=e$.
$f(a)=f(e)=\ln{e}=1$.
$f»(a)=\frac{1}{a}=\frac{1}{e}$.
$y=1+\frac{1}{e}(x-e)=1+\frac{x}{e}-\frac{e}{e}=\frac{x}{e}$.
Уравнение касательной в точке $х=е$ представляет собой функцию $y=\frac{x}{e}$.
Давайте построим график натурального логарифма и касательной.

Пример.
Исследовать функцию на монотонность и экстремумы: $y=x^6-6*ln{x}$.
Решение.
Область определения функции $D(y)=(0;+∞)$.
Найдем производную заданной функции:
$y»=6*x^5-\frac{6}{x}$.
Производная существует при всех х из области определения, тогда критических точек нет. Найдем стационарные точки:
$6*x^5-\frac{6}{x}=0$.
$\frac{6*x^6-6}{x}=0$.
$6*x^6-6=0$.
$x^6-1=0$.
$x^6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания: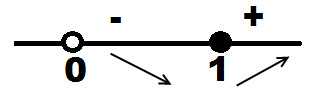
Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $}

Что же такое число е и откуда оно взялось?

Кто-то спросит: «Что же это за число такое удивительное?» И здесь всего три слова: “второй замечательный предел”. На языке математики это выглядит следующим образом:

Расходимся…

Появление числа е связывают с Якобом Бернулли, который еще в 17 веке задался вопросом: какова же максимальная величина процентного дохода при постоянной капитализации вклада?

Якоб Бернулли (1654-1705)

Чтобы было понятно о чем идет речь, давайте представим, что у меня есть рубль. Я кладу его в банк под 100% годовых. То есть, через год у меня уже не рубль, а два.

Но что если рост происходит не мгновенно в конце года, а частями? Ну скажем, каждые полгода по 50%. Да, наш рубль так же превратится в два, но на 50 копеек, которые набежали за первые полгода, за вторую половину года набежит уже свой процент. И мы получим еще 25 копеек дополнительно. И в итоге мы имеем уже 2 рубля 25 копеек.

Если рост вклада будет происходить каждые четыре месяца, то есть 3 раза в год, дополнительный процент к нашим двум рублям, составит уже 37 копеек.

При ежемесячном росте только на процентах у нас набежит примерно 61 копейка.

И здесь возникает вопрос: а что если рост будет происходить непрерывно? Как в природе. К примеру, дети не вырастают на 15 сантиметров в свой день рождения. Нет. Они растут в течении всего года. Каждый день, каждый час, каждую секунду… Что если так же будет расти наш вклад, и вместе с ним будут увеличиваться начисления по проценту?

Существует ли какой то предел при непрерывном росте, который позволит понять, на какую максимальную прибыль мы можем рассчитывать?

Сам Бернулли определил, что это где-то между 2,5 и 3.

Леонард Эйлер (1707 – 1783)

Более точно этот предел вычислил Леонард Эйлер, а полученное число, к которому этот предел стремится, назвал числом е.

По одной из версий е — это первая буква в фамилии ученого (Euler). Но это не точно. Вполне возможно, что е это просто первая буква в слове«экспоненциальный» (exponential). Что тоже кажется тоже вполне разумным, так как экспонента, наверно, первая ассоциация при упоминании числа е. По крайней мере, у меня.

Возведение в степень и логарифм

Возведение в степень представляет собой операцию повторяющегося умножения числа на само себя. Если нам требуется умножить тройку на себя 7 раз, то мы записываем это как 3 × 3 × 3 × 3 × 3 × 3 × 3. Компактная запись такого выражения выглядит как 37 — это и есть возведение в степень.

Деление — операция, обратная умножению. Если верно выражение A × B = C, то и выражение A = C / B так же верно. Такая взаимосвязь часто используется при решении линейных уравнений вида Ax + B = 0, где мы легко можем выразить неизвестное при помощи операции деления. Но что делать, если уравнение не линейное, а показательное? Например, как решить уравнение вида Ax = B. Икс — показатель степени и он нам неизвестен. Возникает задача, в какую степень требуется возвести A, чтобы получить B?

Для наглядности попробуем решить не абстрактный буквенный пример Ax = B, а числовой. Пусть есть элементарное показательное уравнение 2x = 4. В какую степень нужно возвести двойку, чтобы получить 4? Очевидно, что во вторую. Более сложное уравнение 3x = 243. Для решения такого уравнения можно постепенно умножать тройку на саму себя, пока не получим число 243. Легко подсчитать, что 3 × 3 × 3 = 27, но этого мало. Умножим еще на 3 и получим 81. Умножив еще раз мы получим искомое 243. Мы умножили 3 на себя 5 раз, следовательно, x = 5.

Ну а что делать с уравнением 2x = 5? Небольшое изменение, и элементарное уравнение превращается в практически не разрешимое вручную. Очевидно, что ответ больше 2 и меньше 3, но его точное значение мы можем узнать лишь с заданной точностью. Вот тут нам и пригодятся логарифмы. Для решения уравнения следует записать x = log2 5. Все, это и есть ответ, которого достаточно любому математику.

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

Тогда любое число, либо переменную у можно представить в виде:

где х — любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

Воспользуемся свойством

Отсюда получаем универсальную формулу:

В частности, если z=e, то тогда:

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1. Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если

Задача 2. Решите уравнение (5 + 3 * ln (x — 3)) = 3.

Решение: Используя определение логарифма: если

Тогда:

Еще раз применим определение логарифма:

Таким образом:

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

Перед нами квадратное уравнение. Найдем его дискриминант:

Первый корень уравнения:

Второй корень уравнения:

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

Используя определение логарифма: если 

Вспомним, что область определения:

Внимание! Когда в логарифмических уравнениях у вас получается два корня или больше, не забывайте про область определения. Аргумент, стоящий под логарифмом никогда не может быть меньше нуля

Если одно из решений делает выражение под логарифмом меньше либо равным нулю — такой корень вам не подходит, исключите его.