Работа с основанием и показателем степени
Встречаются степени, в основании и/или показателе которых находятся не просто числа или переменные, а некоторые выражения. В качестве примера приведем записи (2+0,3·7) 5−3,7
и (a·(a+1)−a 2) 2·(x+1)
.
При работе с подобными выражениями можно как выражение в основании степени, так и выражение в показателе заменить тождественно равным выражением на ОДЗ его переменных. Другими словами, мы можем по известным нам правилам отдельно преобразовывать основание степени, и отдельно – показатель. Понятно, что в результате этого преобразования получится выражение, тождественно равное исходному.
Такие преобразования позволяют упрощать выражения со степенями или достигать других нужных нам целей. Например, в упомянутом выше степенном выражении (2+0,3·7) 5−3,7
можно выполнить действия с числами в основании и показателе, что позволит перейти к степени 4,1 1,3
. А после раскрытия скобок и приведения подобных слагаемых в основании степени (a·(a+1)−a 2) 2·(x+1)
мы получим степенное выражение более простого вида a 2·(x+1)
.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
\
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
\
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Понятие о степени с иррациональным показателем
Пусть а — какое-нибудь положительное число и а — иррациональное. Какой смысл следует придать выражению ?
Чтобы сделать изложение более наглядным, проведем его на частном примере. Именно, положим а = 2 и а = 1,624121121112…. Здесь, а — бесконечная десятичная дробь, составленная по такому закону: начиная с четвертого десятичного знака, для изображения а употребляются только цифры 1 и 2, и при этом количество цифр 1, записываемых подряд перед цифрой 2, все время увеличивается на одну. Дробь а непериодическая, так как иначе количество цифр 1, записываемых подряд в его изображении, было бы ограниченным. Следовательно, а — иррациональное число.
Итак, какой же смысл следует придать выражению
Чтобы ответить на этот вопрос, составим последовательности значений а с недостатком и избытком с точностью до . Получим
1,6; 1,62; 1,624; 1,6241; …, (1)
1,7; 1,63; 1,625; 1,6242; … (2)
Составим соответствующие последовательности степеней числа 2:

Последовательность (3) возрастает, так как возрастает последовательность (1) (теорема 2 § 6).
Последовательность (4) убывает, так как убывает последовательность (2).
Каждый член последовательности (3) меньше каждого члена последовательности (4), и, таким образом, последовательность (3) ограничена сверху, а последовательность (4) ограничена снизу.
На основании теоремы о монотонной ограниченной последовательности каждая из последовательностей (3) и (4) имеет предел. Если теперь окажется, что разность последовательностей (4) и (3) сходится к нулю, то из этого будет вытекать, что обе эти последовательности, имеют общий предел.
Разность первых членов последовательностей (3) и (4)
![]()
Разность вторых членов
![]()
Разность n-х членов
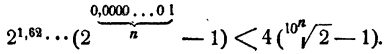
На основании теоремы 3 § 6
Итак, последовательности (3) и (4) имеют общий предел. Этот предел является единственным вещественным числом, которое больше всех членов последовательности (3) и меньше всех членов последовательности (4), его и целесообразно считать точным значением .
Из сказанного вытекает, что и вообще целесообразно принять следующее определение:
Определение:
Если a > 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых есть рациональные приближения а с недостатком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с избытком.
Если a < 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых — рациональные приближения а с избытком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с недостатком.
.Если а= 1, то степенью его с иррациональным показателем а является 1.
Пользуясь понятием предела, это определение можно сформулировать так:
Степенью положительного числа с иррациональным показателем а называется предел, к которому стремится последовательность рациональных степеней этого числа при условии, что последовательность показателей этих степеней стремится к а, т. е.
Пример:
Вычислить с точностью до 0,1 число , если а= 1,624121121112 … (а то же, что и выше).
Решение:
Для приближенного вычисления заметим, что

Далее,
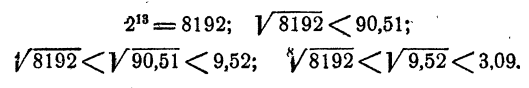
Таким образом, < 3,09.
Испытанием уходим, что (3,03)⁵ = 255,3954324543 < 256. Поэтому . Выходит, что
Число вычислено с точностью до: 0,06.
Возведение в целую степень
Возведение в целую степень удобно рассматривать для трех случаев: для целых положительных показателей, для нулевого показателя, и для целых отрицательных показателей степени.
Так как множество целых положительных чисел совпадает со множеством натуральных чисел, то возведение в целую положительную степень есть возведение в натуральную степень. А этот процесс мы рассмотрели в предыдущем пункте.
Переходим к возведению в нулевую степень. В статье мы выяснили, что нулевая степень числа a определяется для любого отличного от нуля действительного числа a, при этом a=1.
Таким образом, возведение любого отличного от нуля действительного числа в нулевую степень дает единицу. Например, 5=1, (−2,56)=1 и , а 0 не определяется.
Чтобы закончить с возведением в целую степень, осталось разобраться со случаями целых отрицательных показателей. Мы знаем, что степень числа a с целым отрицательным показателем −z определяется как дробь вида . В знаменателе этой дроби находится степень с целым положительным показателем, значение которой мы умеем находить. Осталось лишь рассмотреть несколько примеров возведения в целую отрицательную степень.
Пример.
Вычислите значение степени числа 3 с целым отрицательным показателем −2.
Решение.
По определению степени с целым отрицательным показателем имеем . Значение степени в знаменателе легко находится: 23=2·2·2=8. Таким образом, .
Ответ:
.
Пример.
Найдите значение степени (1,43)−2.
Решение.
. Значение квадрата в знаменателе равно произведению 1,43·1,43. Найдем его значение, выполнив :
Итак, . Запишем полученное число в виде обыкновенной дроби, умножив числитель и знаменатель полученной дроби на 10 000 (при необходимости смотрите преобразование дробей), имеем .
На этом возведение в степень завершено.
Ответ:
.
В заключение этого пункта стоит отдельно остановиться на возведении в степень −1. Минус первая степень числа a равна числу, обратному числу a. Действительно, . Например, 3−1=1/3, и .
Какие правила применяются для возвышения дроби в степень?
Для возвышения дроби в степень применяются определенные правила, которые позволяют проводить вычисления с такими числами. При возведении дроби в степень, необходимо умножить числитель и знаменатель дроби на себя столько раз, сколько указывает показатель степени.
Например, чтобы возвести дробь 2/5 во вторую степень, нужно умножить числитель и знаменатель дроби на себя:
- Числитель: 2 * 2 = 4
- Знаменатель: 5 * 5 = 25
В итоге получаем дробь 4/25.
Если показатель степени отрицательный, то вначале необходимо возвести дробь в положительную степень, а затем взять обратное значение результата. Например, для дроби 3/7, возведенной в степень -2, сначала находим ее значение в положительной степени:
- Числитель: 3 * 3 = 9
- Знаменатель: 7 * 7 = 49
Получаем дробь 9/49. Затем берем ее обратное значение, получая окончательный результат: 49/9.
Таким образом, при возвышении дроби в степень необходимо умножить числитель и знаменатель дроби на себя столько раз, сколько указано в показателе степени. При отрицательном показателе степени необходимо возвести дробь в положительную степень, а затем взять обратное значение результата.
Одна степень
Степень – это математическая операция, которая позволяет возвести число в определенную степень. Возвести дробь в степень – это значит умножить эту дробь саму на себя столько раз, сколько указано в степени.
Если дробь возводится в положительную степень, то результат будет равен произведению дроби на себя столько раз, сколько указано в степени.
Например, если у нас есть дробь 1/2 и мы хотим возвести ее в степень 3, то результат будет равен 1/2 * 1/2 * 1/2 = 1/8.
Если же дробь возводится в отрицательную степень, то мы должны возвести ее в положительную степень, а затем взять обратное значение от полученного результата. То есть, если мы хотим возвести дробь 1/2 в степень -3, то сначала возводим ее в степень 3: 1/2 * 1/2 * 1/2 = 1/8, а затем берем обратное значение: 8/1 = 8.
Отрицательная степень
Возвести дробь в отрицательную степень означает взять обратное значение этой дроби и вознести его в положительную степень. Например, чтобы возвести дробь 1/2 в отрицательную степень -2, нужно сначала взять обратное значение дроби, что будет равно 2/1, а затем возвести это значение в положительную степень 2. Таким образом, (1/2)^(-2) = (2/1)^2 = 4/1 = 4.
При возвели дроби в отрицательную степень, важно помнить, что знаменатель дроби не может быть равен нулю, так как деление на ноль не определено. Если знаменатель дроби равен нулю, то возвести эту дробь в отрицательную степень невозможно
Если число возводится в отрицательную степень, то его обратное значение будет равно единице деленной на это число. То есть, если a = 2, то a^(-1) = 1/2.
Когда дробь возводится в отрицательную степень, ее числитель и знаменатель меняются местами. Например, для дроби 3/4 в степени -1 получим 4/3.
Иногда результат возвели дроби в отрицательную степень может быть представлен в виде обыкновенной десятичной дроби. В этом случае, десятичная дробь может быть округлена до определенного количества знаков после запятой или представлена в виде бесконечной периодической десятичной дроби. Например, (1/3)^(-2) = (3/1)^2 = 9/1 = 9, что соответствует десятичной дроби 9.
Степень больше 1
Когда нужно возвести дробь в степень, большую чем 1, необходимо умножить дробь на себя столько раз, сколько указано в степени. Для этого нужно перемножить числитель и знаменатель дроби каждый раз, когда они участвуют в умножении. Например, чтобы возвести дробь 3/4 в степень 3, нужно умножить числитель (3) на себя 3 раза и знаменатель (4) на себя 3 раза.
Вычисления можно упростить, если обратить внимание на свойства степеней. Если степень больше 1, то результат будет числителем возводимой дроби в эту степень, а знаменатель останется прежним
Например, если нужно возвести дробь 2/5 в степень 4, то результат будет 2^4/5 = 16/5.
Если степень отрицательная, то нужно сначала возвести дробь в положительную степень, а затем взять обратное значение. Например, чтобы возвести дробь 1/3 в степень -2, нужно сначала возвести ее в положительную степень 2, получив 1/9, а затем взять обратное значение 9/1 = 9.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 21 , 174367 .
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Использование дробей в качестве степеней значительно упрощает жизнь по сравнению с записью выражений с помощью корней. Это связано с тем, что совершать арифметические действия с дробями легче, чем применять и помнить свойства корней. Поэтому ниже мы рассмотрим, как перейти от корней к числу в дробной степени.
Возведение в дробную степень проводится соответственно следующему правилу:
Пусть $frac
$ — обыкновенная дробь, причём $p$ и $q$ больше нуля и $q≠1$. Тогда для возведения числа $a$ в дробную степень необходимо извлечь из него корень $q$-ой степени и возвести в степень числителя, равную $p$.
В математической форме это тождество записывается так:
Следует отметить, что в случае использования в качестве записи дробной степени вместо корней есть одно важное правило. Запрещается возводить в дробную степень отрицательные числа
Это связано с тем, что в таком случае можно прийти к невыполнимому равенству, например:
Попробуй обратиться за помощью к преподавателям
Правило для возведения степени в степень в случае, когда показатель степени является дробным числом, выполняется также как и для обычной целой степени, то есть:
Число $a$ в дробной степени вида $frac
$, возведённое в степень $b$, равно числу $a$, возведённому в степень произведения дроби и числа $b$.
В математической форме это выглядит так:
Правило для возведения числа в дробную степень справедливо не только для обыкновенных дробей, но и для десятичных и неправильных.
В случае, если необходимо возвести число в десятичную или неправильную дробь, сначала необходимо перевести её в обычную чтобы стали видны показатели степени числа и корня.
Возведение в нецелую отрицательную степень проводится по тем же правилам, что и возведение в целую отрицательную степень, то есть:
Пусть $frac
$ — обыкновенная дробь и $q≠1$, а $a>0$, тогда $a^<-frac
>$ равно $frac<1>
>>$.
Задай вопрос специалистам и получи ответ уже через 15 минут!
Запишем в математической форме:
Вычислите арифметические корни из следующих выражений:
Решение:
Так и не нашли ответ на свой вопрос?
Просто напиши с чем тебе нужна помощь
Урок и презентация на тему: «Степень с отрицательным показателем. Определение и примеры решения задач»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Определение степени с отрицательным показателем
Мы хорошо знаем, что любое число в нулевой степени равно единице. $a^0=1$, $a≠0$.
Возникает вопрос, а что будет, если возвести число в отрицательную степень? Например, чему будет равно число $2^{-2}$?
Первые математики, задавшиеся этим вопросом, решили, что изобретать велосипед заново не стоит, и хорошо, чтобы все свойства степеней оставались прежними. То есть при умножении степеней с одинаковым основанием, показатели степени складываются.
Давайте рассмотрим такой случай: $2^3*2^{-3}=2^{3-3}=2^0=1$.
Получили, что произведение таких чисел должно давать единицу. Единица в произведении получается при перемножении обратных чисел, то есть $2^{-3}=\frac{1}{2^3}$.
Такие рассуждения привели к следующему определению.
Определение. Если $n$ – натуральное число и $а≠0$, то выполняется равенство:
$a^{-n}=\frac{1}{a^n}$.
Важное тождество, которое часто используется: $(\frac{a}{b})^{-n}=(\frac{b}{a})^n$.
В частности, $(\frac{1}{a})^{-n}=a^n$
Примеры решения
Решение. Рассмотрим каждое слагаемое по отдельности.
1. $2^{-3}=\frac{1}{2^3}=\frac{1}{2*2*2}=\frac{1}{8}$.
2. $(\frac{2}{5})^{-2}=(\frac{5}{2})^2=\frac{5^2}{2^2}=\frac{25}{4}$.
3. $8^{-1}=\frac{1}{8}$.
Осталось выполнить операции сложения и вычитания: $\frac{1}{8}+\frac{25}{4}-\frac{1}{8}=\frac{25}{4}=6\frac{1}{4}$.
Ответ: $6\frac{1}{4}$.
Пример 2. Представить заданное число в виде степени простого числа
$\frac{1}{729}$.
Решение. Очевидно, что $\frac{1}{729}=729^{-1}$.
Но 729 — не простое число, заканчивающиеся на 9. Можно предположить, что это число является степенью тройки. Последовательно разделим 729 на 3.
1) $\frac{729}{3}=243$; 2) $\frac{243}{3}=81$; 3) $\frac{81}{3}=27$; 4) $\frac{27}{3}=9$; 5) $\frac{9}{3}=3$; 6) $\frac{3}{3}=1$.
Выполнено шесть операций и значит: $729=3^6$.
Для нашей задачи:
$729^{-1}=(3^6)^{-1}=3^{-6}$.
Ответ: $3^{-6}$.
Пример 3. Представьте выражение в виде степени:
$\frac{a^6*(a^{-5})^2}{(a^{-3}*a^8)^{-1}}$.
Решение. Первое действие выполняется всегда внутри скобок, затем умножение
$\frac{a^6*(a^{-5})^2}{(a^{-3}*a^8)^{-1}}=\frac{a^6*a^{-10}}{(a^5)^{-1}}=\frac{a^{(-4)}}{a^{(-5)}}=a^{-4-(-5)}=a^{-4+5}=a$.
Ответ: $a$.
Пример 4. Докажите тождество:
$(\frac{y^2 (xy^{-1}-1)^2}{x(1+x^{-1}y)^2}*\frac{y^2(x^{-2}+y^{-2})}{x(xy^{-1}+x^{-1}y)}):\frac{1-x^{-1} y}{xy^{-1}+1}=\frac{x-y}{x+y}$.
Решение.
В левой части рассмотрим каждый сомножитель в скобках отдельно.
1.
$\frac{y^2(xy^{-1}-1)^2}{x(1+x^{-1}y)^2}=\frac{y^2(\frac{x}{y}-1)^2}{x(1+\frac{y}{x})^2}
=\frac{y^2(\frac{x^2}{y^2}-2\frac{x}{y}+1)}{x(1+2\frac{y}{x}+\frac{y^2}{x^2})}=\frac{x^2-2xy+y^2}{x+2y+\frac{y^2}{x}}=\frac{x^2-2xy+y^2}{\frac{x^2+2xy+y^2}{x}}=\frac{x(x^2-2xy+y^2)}{(x^2+2xy+y^2)}$.
2. $\frac{y^2(x^{-2}+y^{-2})}{x(xy^{-1}+x^{-1}y)}=\frac{y^2(\frac{1}{x^2}+\frac{1}{y^2})}{x(\frac{x}{y}+\frac{y}{x})}
=\frac{\frac{y^2}{x^2}+1}{\frac{x^2}{y}+y}=\frac{\frac{y^2+x^2}{x^2}}{{\frac{x^2+y^2}{y}}}=\frac{y^2+x^2}{x^2} *\frac{y}{x^2+y^2}=\frac{y}{x^2}$.
3. $\frac{x(x^2-2xy+y^2)}{(x^2+2xy+y^2)}*\frac{y}{x^2}=\frac{y(x^2-2xy+y^2)}{x(x^2+2xy+y^2)}=\frac{y(x-y)^2}{x(x+y)^2}$.
4. Перейдем к дроби, на которую делим.
$\frac{1-x^{-1}y}{xy^{-1}+1}=\frac{1-\frac{y}{x}}{\frac{x}{y}+1}=\frac{\frac{x-y}{x}}{\frac{x+y}{y}}=\frac{x-y}{x}*\frac{y}{x+y}=\frac{y(x-y)}{x(x+y)}$.
5. Выполним деление.
$\frac{y(x-y)^2}{x(x+y)^2}:\frac{y(x-y)}{x(x+y)}=\frac{y(x-y)^2}{x(x+y)^2}*\frac{x(x+y)}{y(x-y)}=\frac{x-y}{x+y}$.
Получили верное тождество, что и требовалось доказать.
В конце урока еще раз запишем правила действий со степенями, здесь показатель степени — это целое число.
$a^s*a^t=a^{s+t}$.
$\frac{a^s}{a^t}=a^{s-t}$.
$(a^s)^t=a^{st}$.
$(ab)^s=a^s*b^s$.
$(\frac{a}{b})^s=\frac{a^s}{b^s}$.
Задачи для самостоятельного решения
В этой статье мы разберемся, что такое степень числа
. Здесь мы дадим определения степени числа, при этом подробно рассмотрим все возможные показатели степени, начиная с натурального показателя, заканчивая иррациональным. В материале Вы найдете массу примеров степеней, покрывающих все возникающие тонкости.
Навигация по странице.
Возведение в отрицательную степень
Минусовая степень обозначает, что число множат на него самого такое количество раз, какое значится в ст., а после этого единицу делят на вычисленный результат.
Для наглядности следует обратить внимание на такую цепочку выражений:
110=0,1=1* 10 в минус 1 ст.,
1100=0,01=1*10 в минус 2 степ.,
11000=0,0001=1*10 в минус 3 ст.,
110000=0,00001=1*10 в минус 4 степeни.
Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени. Для этой цели достаточно банально сдвигать десятичную составляющую:
- 10 в -1 степeни — перед единицей 1 ноль;
- в -3 — три нуля перед единицей;
- в -9 — это 9 нулей и проч.
Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —
1100000=0,000001=(1*10)-5.

Возведение числа в степень с натуральным показателем
Прежде чем приступить к изучению операции возведения в степень необходимо рассмотреть базовое понятие натуральной степени числа.
Определение
Натуральной степенью n числа а называют произведение, состоящее из n множителей, каждый из которых равен a.
Таким образом, для натурального показателя степень представляет собой укороченную запись умножения одинаковых множителей. В данном случае чтобы найти значение степени, следует перемножить число, которое является основанием, само на себя указанное количество раз.
Пример 1
Рассмотрим возведение числа 3 в степень 5. Согласно приведенному выше базовому определению:
35 = 3 × 3 × 3 × 3 × 3 = 243
Для операций возведения во вторую и третью степень имеются устоявшиеся названия: возведение в квадрат и куб, соответственно. Таким образом, выражение «32» может быть прочитано как «три во второй степени» или «три в квадрате», оба варианта будут верными.
Значение степенных выражений с дробным основанием и натуральным показателем находится по той же схеме. В то же время, в соответствии с правилом умножения дробей, операция возведения дроби в степень может быть разбита на два действия, когда числитель и знаменатель возводятся в соответствующую показателю степень по отдельности.
Пример 2
Найдем, чему будут равны \ в степени 3:
\
Операция возведения в натуральную степень имеет определенные особенности при работе с отрицательными числами. Рассмотрим следующий пример:
Пример 3
Найдем значения степенных выражений (-5)3 и (-5)4. Для этого, согласно базовому определению, необходимо умножить основание само на себя 3 и 4 раза соответственно:
(-5)3 = (-5) × (-5) × (-5) = -125
(-5)4 =(-5) × (-5) × (-5) × (-5) = 625
Из приведенного примера можно видеть, что в первом случае полученный результат является отрицательным числом, а во втором – положительным. Это связано с правилом перемножения отрицательных чисел. Следствием из него является то, что если показатель степени отрицательного числа представляет собой четное число, результат будет положительным, если нечетное – отрицательным. Таким образом, степень с отрицательным основанием и четным показателем будет равна степени с таким же показателем и основанием, равным по модулю, но противоположным по знаку.
(-a)2n = a2n
Если требуется возвести в натуральную степень иррациональное число, то его необходимо предварительно округлить до той значащей цифры, которая позволит получить ответ с требуемой точностью. Рассмотрим данный случай на примере числа π.
Пример 4
Выполним возведение в степень 3 числа π.
π – это бесконечное иррациональное число. С точностью до 10 знаков после запятой оно записывается следующим образом:
π = 3,1415926536
Допустим, нам необходим результат с точностью два знака после запятой. Тогда число π может быть округлено до 3,14.
(3,14)3 = 3,14 × 3,14 × 3,14 ≈ 30,96
Отдельно следует отметить, чему будет равно число в степени 1. В соответствии с базовым определением
\
вне зависимости от значения основания, число в степени 1 равно самому себе.
На практике возможны и более сложные случаи, когда требуется найти значение степенного выражения, в котором показатель не является натуральным числом. Ниже будут рассмотрены ситуации, когда показатель степени представляет собой целое, дробное, рациональное или иррациональное число.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 21 , 174367 .
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Формулы возведения в степень
Чтобы грамотно возводить в степень нужно помнить и знать формулы, указанные ниже. В этом нет ничего сверх естественного, главное понять суть и тогда они не только запомнятся, но и покажутся легкими.
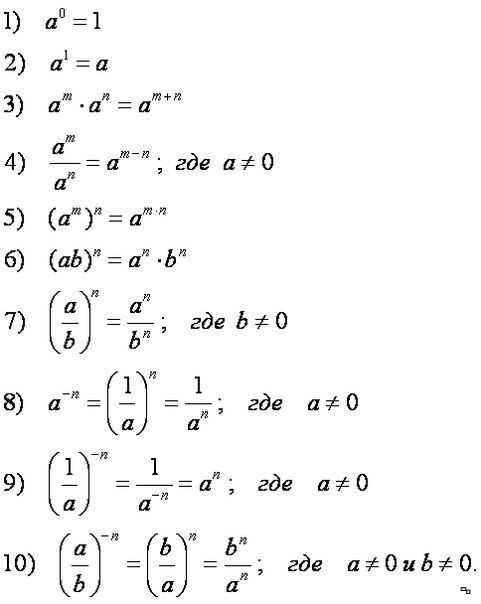
Возведение одночлена в степень
Что из себя представляет одночлен? Это произведение чисел и переменных в любом количестве. Например, двух – одночлен. И вот именно о возведении в степень таких одночленов данная статья.
Пользуясь формулами возведения в степень вычислить возведение одночлена в степень будет не трудно.
Например, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6
; Если возводить одночлен в степень, то в степень возводится каждая составная одночлена.
Возводя в степень переменную уже имеющую степень, то степени перемножаются. Например, (x^2)^3 = x^(2 * 3) = x^6
;
Возведение в отрицательную степень
Отрицательная степень – обратное число. Что такое обратное число? Любому числу Х обратным будет 1/X. То есть Х-1=1/X. Это и есть суть отрицательной степени.
Рассмотрим пример (3Y)^-3:
(3Y)^-3 = 1/(27Y^3).
Почему так? Так как в степени имеется минус, то просто переносим в знаменатель данное выражение, а затем возводим в его в третью степень. Просто не так ли?
Возведение в дробную степень
Начнем рассмотрение вопрос на конкретном примере. 43/2. Что означает степень 3/2? 3 – числитель, означает возведение числа (в данном случае 4) в куб. Число 2 – знаменатель, это извлечение корня второй степени из числа (в данном случае 4).
Тогда получаем квадратный корень из 43 = 2^3 = 8
. Ответ: 8.
Итак, знаменатель дробной степени может быть, как 3, так и 4 и до бесконечности любым числом и это число определяет степень квадратного корня, извлекаемого из заданного числа. Конечно же, знаменатель не может быть равным нулю.
Возведение корня в степень
Если корень возводится в степень, равной степени самого корня, то ответом будет подкоренное выражение. Например, (√х)2 = х. И так в любом случае равенства степени корня и степени возведения корня.
Если (√x)^4. То (√x)^4=x^2. Чтобы проверить решение переведем выражение в выражение с дробной степенью. Так как корень квадратный, то знаменатель равен 2. А если корень возводится в четвертую степень, то числитель 4. Получаем 4/2=2. Ответ: x = 2.
В любом случае лучший вариант просто перевести выражение в выражение с дробной степенью. Если не будет сокращаться дробь, значит такой ответ и будет, при условии, что корень из заданного числа не выделяется.
Возведение в степень комплексного числа
Что такое комплексное число? Комплексное число – выражение, имеющее формулу a + b * i; a, b – действительные числа. i – число, которое при возведение в квадрат дает число -1.
Рассмотрим пример. (2 + 3i)^2.
(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Преобразование выражений с корнями и степенями
Часто в выражениях, в которыми требуется провести некоторые преобразования, вместе со степенями с дробными показателями присутствуют и корни. Чтобы преобразовать подобное выражение к нужному виду, в большинстве случаев достаточно перейти только к корням или только к степеням. Но поскольку работать со степенями удобнее, обычно переходят от корней к степеням. Однако, осуществлять такой переход целесообразно тогда, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков (это мы подробно разобрали в статье переход от корней к степеням и обратно
После знакомства со степенью с рациональным показателем вводится степень с иррациональным показателем, что позволяет говорить и о степени с произвольным действительным показателем. На этом этапе в школе начинает изучаться показательная функция
, которая аналитически задается степенью, в основании которой находится число, а в показателе – переменная. Так мы сталкиваемся со степенными выражениями, содержащими числа в основании степени, а в показателе — выражения с переменными, и естественно возникает необходимость выполнения преобразований таких выражений.
Следует сказать, что преобразование выражений указанного вида обычно приходится выполнять при решении показательных уравнений
и показательных неравенств
, и эти преобразования довольно просты. В подавляющем числе случаев они базируются на свойствах степени и нацелены по большей части на то, чтобы в дальнейшем ввести новую переменную. Продемонстрировать их нам позволит уравнение 5 2·x+1 −3·5 x ·7 x −14·7 2·x−1 =0
.
Во-первых, степени, в показателях которых находится сумма некоторой переменной (или выражения с переменными) и числа, заменяются произведениями. Это относится к первому и последнему слагаемым выражения из левой части:5 2·x ·5 1 −3·5 x ·7 x −14·7 2·x ·7 −1 =0
,5·5 2·x −3·5 x ·7 x −2·7 2·x =0
.
Дальше выполняется деление обеих частей равенства на выражение 7 2·x
, которое на ОДЗ переменной x
для исходного уравнения принимает только положительные значения (это стандартный прием решения уравнений такого вида, речь сейчас не о нем, так что сосредоточьте внимание на последующих преобразованиях выражений со степенями):
Теперь сокращаются дроби со степенями, что дает .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению , которое равносильно . Проделанные преобразования позволяют ввести новую переменную , что сводит решение исходного показательного уравнения к решению квадратного уравнения
И. В. Бойков, Л. Д. Романова
Сборник задач для подготовки к ЕГЭ. Ч. 1. Пенза 2003.
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

При решении арифметических и алгебраических задач иногда требуется возвести дробь
в квадрат
. Проще всего это сделать, когда дробь
десятичная – достаточно обычного калькулятора. Однако если дробь
обыкновенная или смешанная, то при возведении такого числа в квадрат
могут возникнуть некоторые затруднения.
Вам понадобится
калькулятор, компьютер, приложение Excel.
Инструкция
Чтобы возвести десятичную дробь
в квадрат
, возьмите инженерный , наберите на нем возводимую в квадрат
дробь
и нажмите на клавишу возведения во вторую степень. На большинстве калькуляторов эта кнопка обозначена как «х²». На стандартном калькуляторе Windows функция возведения в квадрат
выглядит как «x^2». Например, квадрат
десятичной дроби 3,14 будет равен: 3,14² = 9,8596.
Чтобы возвести в квадрат
десятичную дробь
на обычном (бухгалтерском) калькуляторе, умножьте это число само на себя. Кстати, в некоторых моделях калькуляторов предусмотрена возможность возведения числа в квадрат
даже при отсутствии специальной кнопки. Поэтому предварительно ознакомьтесь с инструкцией к конкретному калькулятору. Иногда «хитрого» возведения в степень приведены на задней крышке или на калькулятора. Например, на многих калькуляторах для возведения числа в квадрат
достаточно нажать кнопки «х» и «=».
Для возведения в квадрат
обыкновенной дроби (состоящей из числителя и знаменателя), возведите в квадрат
по отдельности числитель и знаменатель этой дроби. То есть воспользуйтесь следующим правилом:(ч / з)² = ч² / з², где ч – числитель дроби, з – знаменатель дроби.Пример: (3/4)² = 3²/4² = 9/16.
Если возводимая в квадрат
дробь
– смешанная (состоит из целой части и обыкновенной дроби), то предварительно приведите ее к обыкновенному виду. То есть примените следующую формулу:(ц ч/з)² = ((ц*з+ч) / з)² = (ц*з+ч)² / з², где ц – целая часть смешанной дроби.Пример: (3 2/5)² = ((3*5+2) / 5)² = (3*5+2)² / 5² = 17² / 5² = 289/25 = 11 14/25.
Если в квадрат
(не ) дроби приходится постоянно, то воспользуйтесь программой MS Excel. Для этого введите в одну из таблицы следующую формулу: =СТЕПЕНЬ(A2;2) где А2 – адрес ячейки, в которую будет вводиться возводимая в квадрат
дробь
.Чтобы сообщить программе, что с вводимым числом необходимо обращаться как дробь
ю (т.е. не преобразовывать ее в десятичный вид), наберите перед дробь
ю цифру «0» и знак «пробел». То есть для ввода, например, дроби 2/3 нужно ввести: «0 2/3» (и нажать Enter). При этом в строке ввода отобразится десятичное представление введенной дроби. Значение и представление дроби непосредственно в сохранится в исходном виде. Кроме того, при использовании математических функций, аргументами которых обыкновенные дроби, результат также будет представлен в виде обыкновенной дроби. Следовательно квадрат
дроби 2/3 будет представлен как 4/9.
Пришло время ознакомиться с возведением алгебраической дроби в степень
. Это действие с алгебраическими дробями по смыслу степени сводится к умножению одинаковых дробей. В этой статье мы дадим соответствующее правило, и рассмотрим примеры возведения алгебраических дробей в натуральную степень.
Навигация по странице.





























