Свойства степенных функций, построение графиков

Введение

Пропорциональные величины

Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:

y = kx, 

где k — постоянная величина (коэффициент пропорциональности).

График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая

с осью X угол , тангенс которого равен k:

tg = k (рис.8).

Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.

Линейная функция 

Если переменные y и x связаны уравнением 1-ой степени:

где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае — нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.

Обратная пропорциональность

Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x, где  k — постоянная величина. График обратной пропорциональности – гипербола (рис.10). 

У этой кривой две ветви. Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy= k.

Основные характеристики и свойства гиперболы:

1. область определения функции: , область значений: ;
2. функция монотонная (убывающая) при x < 0 и при x > 0, но не монотонная в целом из-за точки разрыва x = 0 (подумайте, почему?);
3. функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
4. нулей функция не имеет.

Квадратичная функция

Это функция:  

где a, b, c — постоянные, .

В простейшем случае имеем:  

График этой функции квадратная парабола — кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.

График функции  

— тоже квадратная парабола того же вида, что и , но её вершина лежит не в начале координат, а в точке с координатами:

Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x2 и дискриминанта D. 

D = b2 – 4ac. 

Эти свойства следуют из анализа корней квадратного уравнения.

Основные характеристики и свойства квадратной параболы:

  — область определения функции: ( т.e. ), а область значений: … 

     (ответьте, пожалуйста, на этот вопрос сами!);

  — функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная;

  — функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая;

  — при D < 0 не имеет нулей. (А что при ?).

Степенная, показательная и логарифмическая функции

Степенная функция

Это функция:  

где a, n – постоянные.

При n = 1 получаем прямую пропорциональность: y = ax;

при n = 2 — квадратную параболу;

при n = -1 — обратную пропорциональность или гиперболу. 

Таким образом, эти функции — частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, следовательно, при n = 0 степенная функция превращается в постоянную величину:  

y = a, т.e. её график — прямая линия, параллельная оси Х, исключая начало координат. Все эти случаи (при a = 1) показаны на рис.13 () и рис.14 ().

Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:

Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным.

На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.

При n = 2 функция чётная и её график симметричен относительно оси Y. 

При n = 3 функция нечётная и её график симметричен относительно начала координат.

Функция y = x3 называется кубической параболой.

На рис.16 представлена функция

Эта функция является обратной к квадратной параболе y = x2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции.

Мы видим по графику, что это двузначная функция (об этом говорит и знак перед квадратным корнем).

Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.

Показательная функция

Функция y = ax, где a — положительное постоянное число, называется показательной функцией.

Аргумент x принимает любые действительные значения; 

в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию.

Так, функция y = 81x имеет при x = 1/4 четыре различных значения: 

y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3.

Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.

Основные характеристики и свойства показательной функции:

   — область определения функции: ( т.e. );

   — область значений: y > 0;

   — функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;

   — функция неограниченная, всюду непрерывная, непериодическая;

   — нулей функция не имеет.

Логарифмическая функция

Пусть а — положительное число, не равное 1.

Определение. Функцию, заданную формулой

называют логарифмической функцией с основанием а.

Перечислим основные свойства логарифмической функции:

1. Область определения логарифмической функции — множество всех положительных чисел R₊, т. е. D(log_a)=R₊. Действительно, каждое положительное число х имеет логарифм по основанию а.
2. Область значений логарифмической функции — множество всех действительных чисел. В самом деле, по определению логарифма любого действительного у справедливо равенство:

т. е. функция y = log_ax принимает значение у в точке x= aу0

3. Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0<а<1).

Докажем, например, что при а>1 функция возрастает (в случае 0 < а < 1 проводится аналогичное рассуждение).

Доказательство:

Пусть x₁ и x₂ — произвольные положительные числа и x₂>x₁. Надо доказать, что log_a x₂>log_a x₁. Допустим противное, т. е. что log_a x₂≤log_a x₁ (3)

Так как показательная функция у = ах при а>1 возрастает, из неравенства (3) следует: alog_a x₂ ≤ alog_a x₁. (4)

Но alog_a x₂ = x₂, alog_a x₁ = x₁ (по определению логарифма), т. е. неравенство (4) означает, что x₂ ≤ x₁. Это противоречит допущению x₂ > x₁.

Для построения графика заметим, что значение 0 логарифмическая функция принимает в точке 1;

log_a 1 = 0 при любом а > 0, так как а = 1.

Вследствие возрастания функции при а > 1 получаем, что при х > 1 логарифмическая функция принимает положительные значения, а при 0 отрицательные.

Если 0 < а <1, то y = log_ax убывает на R₊, поэтому log_a x > 0, при x > 1.

Опираясь на доказанные свойства, нетрудно построить график функции y = log_a х при а>1 (рис. 1, а) и 0<а<1 (рис. 1,6).

Справедливо следующее утверждение:

Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у = х (рис. 2).

Свойства степенной функции с натуральным четным показателем

1. Область определения — все действительные числа.

2. $f\left(-x\right)={(-x)}^{2n}=x^{2n}=f(x)$ — функция четна.

3. $f(x)$ — непрерывна на всей области определения.

4. Область значения — $[0,+\infty )$.

5. $f'(x)=\left(x^{2n}\right)’=2n\cdot x^{2n-1}$

   \ \

   Функция убывает, при $x\in (-\infty ,0)$ и возрастает, при $x\in (0,+\infty )$.

6. $f(x)\ge 0$ на всей области определения

7. $f{»}\left(x\right)={\left(2n\cdot x^{2n-1}\right)}’=2n(2n-1)\cdot x^{2(n-1)}\ge 0$

   Функция выпукла на всей области определения.

8. Поведение на концах области определения:

   \ \

9. График (рис. 2).

График функции $f\left(x\right)=x^{2n}$»>Рисунок 2. График функции $f\left(x\right)=x^{2n}$

Степенная функция при нечетном положительном показателе

Разберем степенную функцию y=xa, когда a – нечетное положительное число, например, a=1, 3, 5…

Для наглядности укажем графики таких степенных функций: y=x(черный цвет графика), y=x3 (синий цвет графика), y=x5 (красный цвет графика), y=x7 (зеленый цвет графика). Когда a=1, получаем линейную функцию y=x.

Определение 6

Свойства степенной функции, когда показатель степени – нечетный положительный

• область определения: x∈-∞; +∞;
• область значений: y∈-∞; +∞;
• функция является нечетной, поскольку y(-x)=-y(x);
• функция является возрастающей при x∈(-∞; +∞);
• функция имеет выпуклость при x∈(-∞; 0] и вогнутость при x∈[0; +∞) (исключая линейную функцию);
• точка перегиба имеет координаты (0; 0) (исключая линейную функцию);
• асимптоты отсутствуют;
• точки прохождения функции: (-1; -1), (0; 0), (1;1).

Что такое степенная функция

Степенная функция является одной из разновидностей алгебраической функции, в которой зависимость между переменными представлена в виде возведения одной переменной в степень другой.

Степенными функциями являются функции вида:

• f(x) = a * xn, где a и n — постоянные значения, а x — переменная;
• f(x) = xn, где n — постоянная степень, а x — переменная.

Степенная функция может быть задана на области действительных или комплексных чисел и имеет некоторые особенности:

1. Значение степенной функции зависит от значения переменной x и степени n.
2. Значение функции может быть отрицательным, положительным или нулевым в зависимости от значений a, n и x.
3. В случае, когда степень n является рациональным числом, функция имеет определенную область значений и может быть ограничена сверху и снизу.
4. Степенная функция может иметь асимптоты или точки разрыва в зависимости от значения n и области определения.
5. Значением n может быть как положительное число, так и отрицательное число.

Данный тип функций широко применяется в различных научных дисциплинах, таких как физика, экономика, геометрия и другие. Степенные функции позволяют описывать различные явления и законы природы, а также анализировать зависимость между переменными в различных моделях и задачах.

Свойства степенной функции с натуральным нечетным показателем

1. Область определения — все действительные числа.

2. $f\left(-x\right)={(-x)}^{2n-1}={-x}^{2n}=-f(x)$ — функция нечетна.

3. $f(x)$ — непрерывна на всей области определения.

4. Область значения — все действительные числа.

5. $f’\left(x\right)=\left(x^{2n-1}\right)’=(2n-1)\cdot x^{2(n-1)}\ge 0$

   Функция возрастает на всей области определения.

6. $f\left(x\right)0$, при $x\in (0,+\infty )$.

7. $f{»\left(x\right)}={\left(\left(2n-1\right)\cdot x^{2\left(n-1\right)}\right)}’=2\left(2n-1\right)(n-1)\cdot x^{2n-3}$

   \ \

   Функция вогнута, при $x\in (-\infty ,0)$ и выпукла, при $x\in (0,+\infty )$.

8. График (рис. 3).

Рисунок 3. График функции $f\left(x\right)=x^{2n-1}$

Что это такое? Основные понятия и определения

Азы алгебраического анализа математики станут пошагово яснее с помощью основных первичных понятий, определений, правил. Так на Рис.1 отображены термины и обозначения (понятийные ключи) направлений при переходе от «Начало» к исследованию функций для переменных в алгебре, к другим разделам царицы наук.

Рис.1

Обучение начинается от простых математических терминов – изначальных определений:

• Переменная – символ в математике, свободная величина (аргумент функции), может принимать любое из ряда значений фиксированной области (вес зависит от возраста теленка, x в алгебре);

• Функция – соответствие (зависимость) между «связанными» изменяемыми элементами; каждое значение зависимой функции определяется конкретной независимой величиной (переменной). Или же это формула, отображающая здравый смысл зависимости переменных (в математике обозначается y= f(x));

• Степень – для общего случая, какая-либо мера в сравнении, в алгебре – это выражение, служащее для упрощения многократного умножения основания x (числа, переменной, функции ) на самое себя (пример обозначения: x^2). Количество одинаковых множителей называется показателем степени. В алгебре показатели степени могут быть целыми (четными и нечетными), дробными и иррациональными;

• Иррациональное число представляют как непериодическую бесконечную десятичную дробь (число = 3,1415926535…);

• Производная – тоже функция (вторичная), образованная от первичной, обозначается Y= f’(x) (как скоростная характеристика движения, как угол наклона касательной к линии);

Степенная функция – это функциональная зависимость вида f(x)=. Например, кубическая (объем) функционально зависит от длины ребра куба (x), его третьей степени (y=).

Гипербола. График функции и свойства.

теория по математике функции

Графиком функции у= k x . . , где k ≠ 0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

Свойства гиперболы (у= k x . )

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

1. Область определения – любое число, кроме нуля.
2. Область значения – любое число, кроме нуля.
3. Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у= 10 x . . .

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.

Теперь для построения гиперболы соединим точки плавной линией. Построить график функции у= − 5 x . . .

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у

При делении обращаем внимание на знаки, чтобы не допускать ошибок

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

• если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
• если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

pазбирался: Даниил Романович | обсудить разбор | оценить

Корень n-й степени

Данная элементарная функция определяется формулой y=xn (n – натуральное число больше единицы).

Рассмотрим две вариации функции.

1. Корень n-й степени, n – четное число

Для наглядности укажем чертеж , на котором изображены графики таких функций: y=x, y=x4 и y=x8. Эти функции отмечены цветом: черный, красный и синий соответственно.

Похожий вид у графиков функции четной степени при иных значениях показателя.

Определение 3

Свойства функции корень n-ой степени, n – четное число

• область определения – множество всех неотрицательных действительных чисел [0, +∞);
• когда x=0, функцияy=xn имеет значение, равное нулю;
• данная функция- функция общего вида (не является ни четной, ни нечетной);
• область значений: [0, +∞);
• данная функция y=xn при четных показателях корня возрастает на всей области определения;
• функция обладает выпуклостью с направлением вверх на всей области определения;
• отсутствуют точки перегиба;
• асимптоты отсутствуют;
• график функции при четных n проходит через точки (0; 0) и (1; 1).

1. Корень n-й степени, n – нечетное число

Такая функция определена на всем множестве действительных чисел. Для наглядности рассмотрим графики функций y=x3, y=x5 и x9. На чертеже они обозначены цветами: черный, красный и синий цвета кривых соответственно.

Иные нечетные значения показателя корня функции y=xn дадут график аналогичного вида.

Определение 4

Свойства функции корень n-ой степени, n – нечетное число

• область определения – множество всех действительных чисел;
• данная функция – нечетная;
• область значений – множество всех действительных чисел;
• функция y=xn при нечетных показателях корня возрастает на всей области определения;
• функция имеет вогнутость на промежутке (-∞; 0] и выпуклость на промежутке [0, +∞);
• точка перегиба имеет координаты (0; 0);
• асимптоты отсутствуют;
• график функции при нечетных n проходит через точки (-1; -1), (0; 0) и (1; 1).

Дробно-линейная функция

Теперь рассмотрим несколько более сложные ф-ции, чьи графики, однако, также представляют собой гиперболу. Пусть есть ф-ция вида

Как будет выглядеть ее график? Для ответа на этот вопрос выполним преобразование:

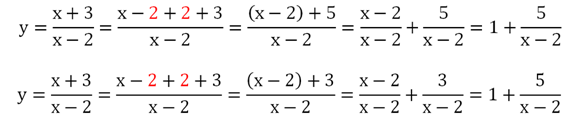
Здесь мы в числителе и знаменателе добавили и сразу вычли слагаемое 2.Этот прием помог нам выделить целую часть из дроби. В результате мы получили ф-цию, график которой можно получить с помощью двух параллельных переносов графика у = 6/х. Сначала график сместится на две единицы вправо:

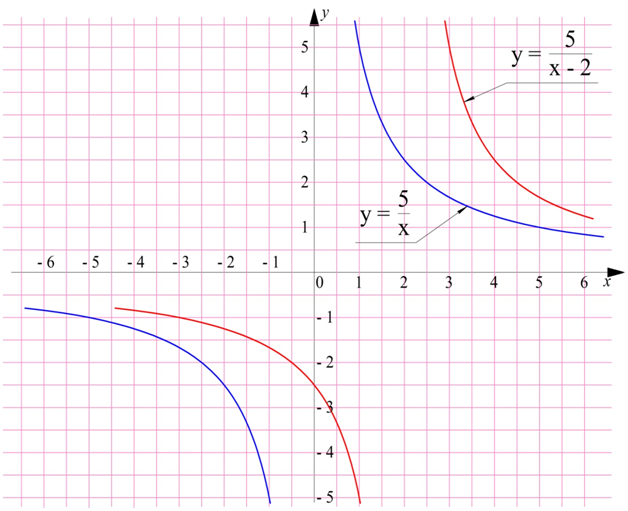
На следующем шаге график поднимется на единицу вверх:

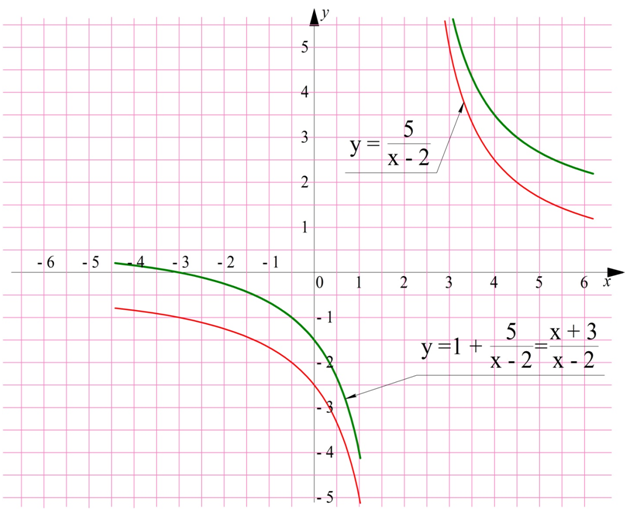
Стоит обратить внимание, что при таком передвижении гиперболы передвигаются и асимптоты графика гиперболы:

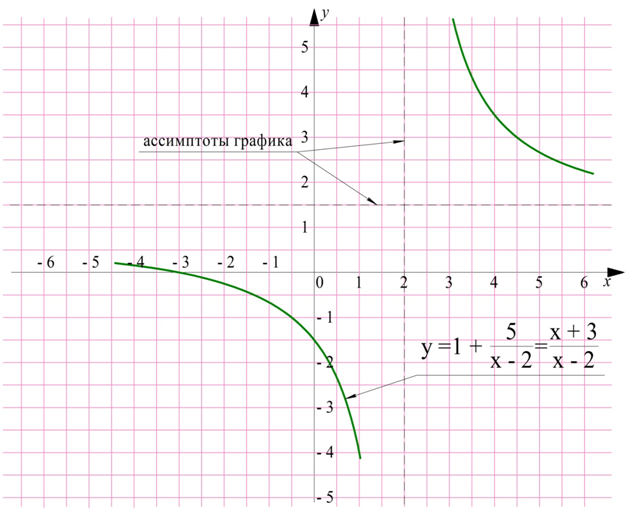
Функция

представляет собой дробь, являющуюся отношением двух линейных многочленов, х + 3 и х – 2. В математике подобные ф-ции называют дробно-линейными функциями. В качестве примеров дробно-линейных функций можно привести:

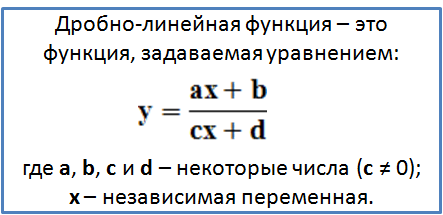
Из любой дробно-линейной функции можно выделить целую часть. Покажем это на нескольких примерах:

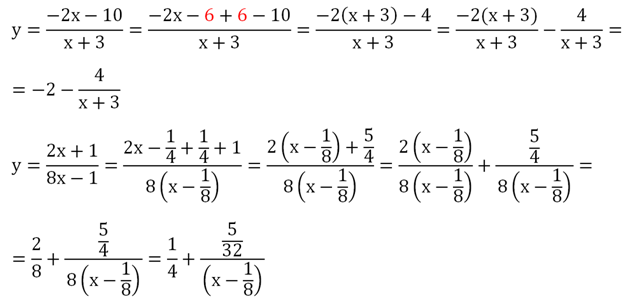
Во всех этих случаях график дробно-линейной функции можно построить с помощью двух параллельных переносов гиперболы.

Однако есть одно исключение. Иногда при выделении из дроби целой части дробной части не остается вовсе, то есть линейные полиномы можно сразу сократить. Например:

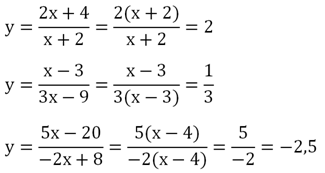
Графиком таких функций являются прямые горизонтальные линии. Однако на них должна быть одна «исключенная». Действительно, пусть надо построить график ф-ции

Проведя преобразования, получим

то есть у = 2. Однако в знаменателе дроби не может стоять ноль. Если же подставить в дробь х = – 2, то получим деление на ноль:

Поэтому график ф-ции будет выглядеть так:

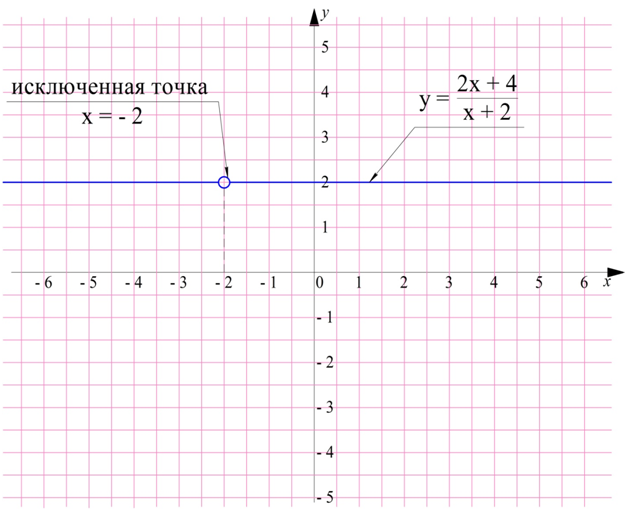
Итак, по итогам урока мы узнали:

1. как растягиваются и сжимаются графики;
2. как графики функций переносятся вверх-вниз и влево-вправо;
3. что такое обратная пропорциональность и как выглядит ее график – гипербола;
4. как выглядит дробно-линейная функция, и каким образом ее график можно получить из гиперболы с помощью параллельных переносов.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж: Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

Виды и их свойства, область определения

Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.

Свойства функции\( y=x^{\frac{m}{n}}, (m>n)\):

• D(y)=[0;+∞);
• функцию нельзя отнести ни к четной, ни к нечетной;
• возрастает на [0;+∞);
• не имеет ограничений в верхней части, но ограничена в нижней;
• отсутствует максимальное значение, минимальное значение равно нулю;
• непрерывность;
• E(f)=[0; +∞);
• выпукла вниз.

В качестве примера можно рассмотреть случай, когда показатель степени является правильной дробью, у которой значение числителя меньше, чем знаменателя. График функции\( y=x^{\frac{m}{n}}\), \((m>n)\) напоминает график функции \(y=\sqrt{x}\):

Свойства функции\( y=x^{\frac{m}{n}}\), \(0<\frac{m}{n}<1:\)

• D(y)=[0;+∞);
• нельзя отнести ни к четной, ни к нечетной;
• возрастает на [0;+∞);
• не имеет ограничений сверху, ограничена снизу;
• максимальное значение отсутствует, наименьшее значение равно нулю;
• непрерывность;
• E(f)=[0; +∞);
• выпукла вверх.

Далее следует ознакомиться с графиком функции \(y=x^{-\frac{m}{n}}\). Можно заметить, что он похож на гиперболу. График обладает двумя асимптотами:

• горизонтальной y=0;
• вертикальной х=0.

График имеет следующий вид:

Свойства функции \(y=x^{-\frac{m}{n}}:\)

• D(y)=(0;+∞);
• не является ни четной, ни нечетной;
• убывает на (0;+∞);
• не ограничена в верхней части, обладает ограничением в нижней;
• максимальное значение отсутствует, минимальное – ноль;
• непрерывность;
• E(f)=(0; +∞);
• выпукла вниз.

В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:

\(y’=r*x^{r-1}\)

К примеру: \((x^{1000})’=1000x^{999} \)

\((x^{-8})’=-8x^{-9}\)

\(\frac{2}{(x^3)’}=\frac{2}{3}*x^{-\frac{1}{3}}\)

\((\sqrt{(2x+5)^5})’=((2x+5)^{\frac{5}{6}})’=2*\frac{5}{6}(2x+5)^{-\frac{1}{6}}=\frac{5}{3}(2x+5)^{-\frac{1}{6}}.\)

Примеры и применение степенных функций

Степенные функции являются одним из наиболее распространенных типов функций и широко применяются в различных областях науки и техники. Ниже приведены несколько примеров и применений степенных функций:

1. Математика: Степенные функции используются для описания зависимости между переменными, где одна переменная возведена в степень другой. Например, функция вида f(x) = x^n, где n — константа, является степенной функцией. Степенные функции играют важную роль в алгебре, геометрии, математическом анализе и других разделах математики.
2. Физика: В физике степенные функции используются для описания различных явлений. Например, закон Гука, описывающий зависимость между силой, действующей на упругое тело, и его деформацией, может быть выражен степенной функцией.
3. Экономика: Степенные функции используются для моделирования различных экономических процессов, таких как рост населения, экономический рост, инфляция и другие. Например, закон Мальтуза, описывающий рост населения, может быть выражен степенной функцией.
4. Биология: В биологии степенные функции часто применяются для описания зависимостей между различными биологическими параметрами. Например, закон вселенной, описывающий количество организмов в экосистеме, может быть выражен степенной функцией.

Это лишь несколько примеров применения степенных функций в различных областях. Из-за их универсальности и широкой применимости, степенные функции находят применение во многих других областях знаний.

На что влияют коэффициенты

Рассмотрим такие функции:

\( \displaystyle y=\frac{1}{x};\text{ }y=\frac{2}{x};\text{ }y=\frac{4}{x};\text{ }y=-\frac{1}{x};\text{ }y=-\frac{3}{x}\):

Ух ты, какая красота!

Все графики построены разными цветами, чтобы легче было их друг от друга отличать.

Итак, на что обратим внимание в первую очередь?

Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси \( \displaystyle Ox\).

Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.

А что, если функция выглядит сложнее, например, \( \displaystyle y=\frac{1}{x-1}+2\)?

В этом случае гипербола будет точно такой же, как обычная \( \displaystyle y=\frac{1}{x}\), только она немного сместится. Давай думать, куда?

Чему теперь не может быть равен \( x\)? Правильно, \( x\ne 1\). Значит, график никогда не достигнет прямой \( x=1\).

А чему не может быть равен \( y\)? Теперь \( y\ne 2\). Значит, теперь график будет стремиться к прямой \( y=2\), но никогда ее не пересечет.

Итак, теперь прямые \( x=1\) и \( y=2\) выполняют ту же роль, которую выполняют координатные оси для функции \( \displaystyle y=\frac{1}{x}\).

Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):

Более подробно о том, как строятся такие графики, мы выучим чуть позже.

А теперь попробуй решить несколько примеров для закрепления.

Степенная функция с рациональным и иррациональным показателем

Определение 5

Степень действительного числа $a$ c рациональным показателем $n$ определяется формулой:

\{a^m}\]

Определение 6

$f\left(x\right)=x^r$ ($r\in Q)$ называется степенной функцией с рациональным показателем.

Определение 7

Степень положительного числа $a$ c иррациональным показателем $\alpha $ называется выражение вида $a^{\alpha }$, значение которого равно пределу последовательности $a^{{\alpha }_0},\ a^{{\alpha }_1},\ a^{{\alpha }_2},\dots $, где ${\alpha }_0,\ {\alpha }_1,{\alpha }_2$ последовательные десятичные приближения иррационального числа $\alpha $.

Определение 8

$f\left(x\right)=x^r$ ($r\in J)$ называется степенной функцией с иррациональным показателем.

Приведем графики степенных функций с рациональным и иррациональным показателем (рис. 5). Рассмотреть, аналогично, свойства этих функции оставим читателю.

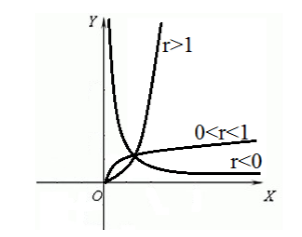Рисунок 6. График функции $f\left(x\right)=x^r$

Степенная функция с целым показателем

Для начала введем понятие степени с целым показателем.

Определение 3

Степень действительного числа $a$ c целым показателем $n$ определяется формулой:

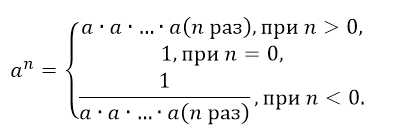Рисунок 4.

Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.

Определение 4

$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем

Логарифмическая функция

Логарифмическая функция имеет вид y=loga(x), где a>0, a≠1.

Такая функция определена только при положительных значениях аргумента: при x∈0; +∞.

График логарифмической функции имеет различный вид, исходя из значения основания а.

Рассмотрим сначала ситуацию, когда 0<a<1. Продемонстрируем этот частный случай графиком логарифмической функции при a=12 (синий цвет кривой) и а=56 (красный цвет кривой).

Иные значения основания, не большие единицы, дадут аналогичный вид графика.

Определение 16

Свойства логарифмической функции, когда основание меньше единицы:

• область определения: x∈0; +∞.  Когда х стремится к нулю справа, значения функции стремятся к +∞;
• область значений: y∈-∞; +∞;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• логарифмическая функция является убывающей на всей области определения;
• функция имеет вогнутость при x∈0; +∞;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точка прохождения функции: (1; 0).

Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а>1. На чертеже ниже –графики логарифмических функций y=log32x и y=ln x (синий и красный цвета графиков соответственно).

Иные значения основания больше единицы дадут аналогичный вид графика.

Определение 17

Свойства логарифмической функции, когда основание больше единицы:

• область определения: x∈0; +∞.  Когда х стремится к нулю справа, значения функции стремятся к -∞;
• область значений: y∈-∞; +∞ (все множество действительных чисел);
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• логарифмическая функция является возрастающей при x∈0; +∞;
• функция имеет выпуклость при x∈0; +∞;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точка прохождения функции: (1; 0).

Принципы построения графика обратной пропорциональности (гиперболы)

Теперь давай научимся строить простейшую гиперболу – ( displaystyle y=frac{k}{x}).

Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.

Например, построим гиперболу ( displaystyle y=frac{3}{x}).

Составим таблицу из ( 4) точек, которые принадлежат одной ветке (например, правой):

( x)	( frac{1}{2})	( displaystyle 1)	( displaystyle 3)	( displaystyle 6)
( y)	( displaystyle 6)	( displaystyle 3)	( displaystyle 1)	( frac{1}{2})

Отмечаем точки на рисунке:

Проводим через них плавную линию, которая краями приближается к осям:

Это одна ветвь гиперболы

Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:

Отлично, осталось вспомнить, что собой представляет вторая ветвь?

Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.

Вот:

Еще один полезный факт.

Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны ( sqrt{k}) для правой ветви гиперболы, и ( -sqrt{k}) для левой.

Для функций, у которых ( k) – точный квадрат (например, ( 1), ( 4) или ( displaystyle frac{1}{4})), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.

В этом случае достаточно даже трех точек, чтобы построить график.

Например, построим график функции ( displaystyle y=frac{4}{x})

Как и в прошлый раз, начнем с правой ветви.

Точка симметрии: ( displaystyle x=y=2). Выберем еще одну точку, например, ( displaystyle x=1), ( displaystyle y=4). У третьей точки координаты будут наоборот: ( displaystyle x=4), ( displaystyle y=1).

Рисуем:

И теперь симметрично отображаем эту ветвь в третью координатную четверть:

Теперь выясним, что будет, если ( displaystyle k<0)?

Очень просто: если есть график функции с таким же по величине, но положительным ( displaystyle k), то нужно просто отразить его относительно оси ( displaystyle Ox)

То есть правая ветвь теперь будет ниже оси ( displaystyle Ox) (в ( displaystyle IV) четверти), а левая – выше (в ( displaystyle III) четверти).

Принцип построения же останется прежним:

Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.