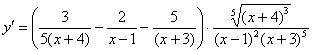Производная обратной функции.
Чтобы
при изложении не было путаницы, давайте
обозначать в нижнем индексе аргумент
функции, по которому выполняется
дифференцирование, то есть, —
это производная функции f(x)
по x
.
Теперь
сформулируем правило
нахождения производной обратной функции.
Пусть
функции y
= f(x)
и x
= g(y)
взаимно
обратные, определенные на
интервалах и соответственно.
Если в точке существует
конечная отличная от нуля производная
функции f(x)
,
то в точке существует
конечная производная обратной
функции g(y)
,
причем .
В другой записи .
Можно
это правило переформулировать для
любого x
из
промежутка ,
тогда получим .
Давайте
проверим справедливость этих формул.
Найдем
обратную функцию для натурального
логарифма (здесь y
–
функция, а x
—
аргумент). Разрешив это уравнение
относительно x
,
получим (здесь x
–
функция, а y
–
ее аргумент). То есть, и взаимно
обратные функции.
Из таблицы
производных видим,
что и .
Убедимся,
что формулы нахождения производных
обратной функции приводят нас к этим
же результатам:
Как
видите, получили такие же результаты
как и в таблице производных.
Теперь
мы обладаем знаниями для доказательства
формул производных обратных
тригонометрических функций.
Начнем
с производной арксинуса.
.
Тогда по формуле производной обратной
функции получаем
Осталось
провести преобразования.
Так
как областью значений арксинуса является
интервал ,
то (смотрите
раздел основные
элементарные функции, их свойства и
графики). Поэтому ,
а не
рассматриваем.
Следовательно, .
Областью определения производной
арксинуса является промежуток (-1;
1)
.
Для
арккосинуса все делается абсолютно
аналогично:
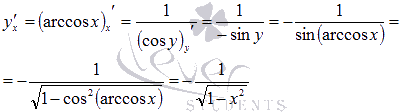
Найдем
производную арктангенса.
Для обратной
функцией является .
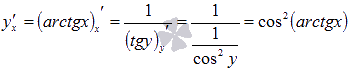
Выразим
арктангенс через арккосинус, чтобы
упростить полученное выражение.
Пусть arctgx
= z
,
тогда
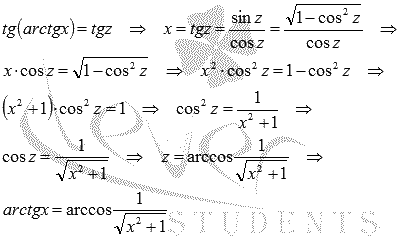
Следовательно,
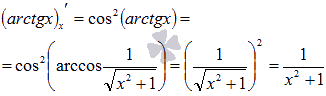
Схожим
образом находится производная
арккотангенса:
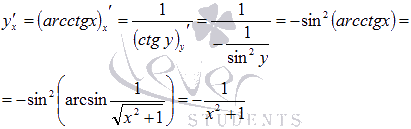
(x)
(x)
показательно-степенной
Заметим, что степенно-показательную функцию можно представить в показательном виде:.
Поэтому ее также называют сложной показательной функцией
.
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1.
Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны
, т.е.
Правило 2.
Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной
:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3.
Если функции
дифференцируемы в некоторой точке
и
, то в этой точке дифференцируемо и их частное
u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
«Производная произведения и частного функций »
.
Замечание.
Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое
u
«v
, в котором u
— число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции
посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями
и Действия с дробями
.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1.
Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны
, т.е.
Правило 2.
Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной
:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3.
Если функции
дифференцируемы в некоторой точке
и
, то в этой точке дифференцируемо и их частное
u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
«Производная произведения и частного функций »
.
Замечание.
Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое
u
«v
, в котором u
— число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции
посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями
и Действия с дробями
.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».
Производные высших порядков
См. Доказательство методом математической
См. Вывод производной степенной функции n-го
См. Производные высших порядков показательной
См. Производные косинуса высших
где См. Производные тангенса высших .
где См. Производные котангенса высших .
Производные арксинуса и арккосинуса
где – многочлен степени Он определяется по формулам: Здесь См. Вывод производных высших порядков арксинуса и .
Производные арктангенса и арккотангенса
Другой вид производных: где где
См. Вывод производных высших порядков арктангенса и .
Примеры вычисления производных Справочник по элементарным функциям
Производные простых функций
Производная от числас´ = 0
Пояснение:
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице x´ = 1
Пояснение:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2 Пояснение:
В данном случае, при каждом изменении аргумента функции (х) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.
Откуда следует, что (cx + b)’ = c то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю |x|’ = x / |x| при условии, что х ≠ 0 Пояснение:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x < 0 оно равно (-1), а когда x > 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу ( xc )’= cxc-1, при условии, что xc и сxc-1,определены а с ≠ 0
Пример:
(x2 )’ = 2x
(x3)’ = 3×2Для запоминания формулы:
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3×2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х (1/х)’ = — 1 / x2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)’ = (x-1 )’ , тогда можно применить формулу из правила 5 таблицы производных
(x-1 )’ = -1x-2 = — 1 / х2
7. Производная дроби с переменной произвольной степени в знаменателе ( 1 / xc )’ = — c / xc+1
Пример:
( 1 / x2 )’ = — 2 / x3
8. Производная корня (производная переменной под квадратным корнем) ( √x )’ = 1 / ( 2√x ) или 1/2 х-1/2
Пример:
( √x )’ = ( х1/2 )’ значит можно применить формулу из правила 5
( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени ( n√x )’ = 1 / ( n n√xn-1 )
.
Приведенная здесь таблица производных простых функций содержит только основные преобразования, которые (по большому счету) следует запомнить наизусть. Нахождение более сложных производных приведены в соответствующих таблицах других уроков:
- Таблица производных экспоненциальных и логарифмических функций
- Таблица производных тригонометрических функций.
2080.1947
Правила дифференцированияОписание курса Таблица производных экспоненциальных и логарифмических функций
Логарифмическая производная
Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.
Пример 11
Найти производную функции
Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.
Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:
Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:
Собственно приступаем к дифференцированию. Заключаем под штрих обе части:
Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.
Как быть с левой частью?
В левой части у нас сложная функция
. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».
Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ
(если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :
В левой части как по мановению волшебной палочки у нас «нарисовалась» производная . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:
А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:
Окончательный ответ: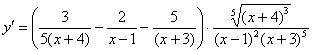
Пример 12
Найти производную функции
Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.
С помощью логарифмической производной можно было решить любой из примеров №№4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1.
Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны
, т.е.
Правило 2.
Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной
:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3.
Если функции
дифференцируемы в некоторой точке
и
, то в этой точке дифференцируемо и их частное
u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
«Производная произведения и частного функций »
.
Замечание.
Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое
u
«v
, в котором u
— число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции
посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями
и Действия с дробями
.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».
Производные гиперболических функций
Доказательство 7
Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
sh’x=ex-e-x2’=12ex’-e-x’==12ex—e-x=ex+e-x2=chxch’x=ex+e-x2’=12ex’+e-x’==12ex+-e-x=ex-e-x2=shxth’x=shxchx’=sh’x·chx-shx·ch’xch2x=ch2x-sh2xch2x=1ch2xcth’x=chxshx’=ch’x·shx-chx·sh’xsh2x=sh2x-ch2xsh2x=-1sh2x
Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.
Производные простых функций
с´ = 0
Пояснение
:
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной
равна единице
x´ = 1
Пояснение
:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение
:
В данном случае, при каждом изменении аргумента функции (х
) ее значение (y) растет в с
раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с
.
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
Производная переменной по модулю
|x|»
Пояснение
отрицательных значениях
5. Производная переменной в степени
равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1
, при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы
:
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби
1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби
с переменной произвольной степени
в знаменателе
(1 / x c)» =
— c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня
(производная переменной под квадратным корнем)
(√x)» = 1 / (2√x)
или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную
, надо выражение под знаком штриха разобрать на составляющие
простые функции
и определить, какими действиями (произведение, сумма, частное)
связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования.
Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1.
Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу.
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2.
Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Вывод формулы производной степенной функции
Случай x > 0
Рассмотрим степенную функцию от переменной x
с показателем степени a
:
(3)
.
Здесь a
является произвольным действительным числом. Сначала рассмотрим случай .
Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:.
Теперь находим производную, применяя :;
.
Здесь .
Формула (1) доказана.
Вывод формулы производной от корня степени n из x в степени m
Теперь рассмотрим функцию, являющуюся корнем следующего вида:(4)
.
Чтобы найти производную, преобразуем корень к степенной функции:.
Сравнивая с формулой (3) мы видим, что.
Тогда.
По формуле (1) находим производную:(1)
;
;
(2)
.
На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).
Случай x = 0
Если ,
то степенная функция определена и при значении переменной x = .
Найдем производную функции (3) при x = .
Для этого воспользуемся определением производной:.
Подставим x = :
.
При этом под производной мы понимаем правосторонний предел, для которого .
Итак, мы нашли:.
Отсюда видно, что при ,
.
При ,
.
При ,
.
Этот результат получается и по формуле (1):(1)
.
Поэтому формула (1) справедлива и при x = .
Случай x
Снова рассмотрим функцию (3):(3)
.
При некоторых значениях постоянной a
,
она определена и при отрицательных значениях переменной x
.
А именно, пусть a
будет рациональным числом. Тогда его можно представить в виде несократимой дроби:,
где m
и n
— целые числа, не имеющие общего делителя.
Если n
нечетное, то степенная функция определена и при отрицательных значениях переменной x
.
Например, при n = 3
и m = 1
мы имеем кубический корень из x
:
.
Он определен и при отрицательных значениях переменной x
.
Найдем производную степенной функции (3) при и при рациональных значениях постоянной a
,
для которых она определена. Для этого представим x
в следующем виде:.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции :.
Здесь .
Но.
Поскольку ,
то.
Тогда.
То есть формула (1) справедлива и при :
(1)
.