Тождественные преобразования

Разница в определении

Одним из важных отличий между тождеством и равенством является их определение.

• Тождество — это выражение, которое всегда истино, независимо от значений переменных.
• Равенство — это выражение, которое истинно только тогда, когда значения переменных равны друг другу.

Таким образом, тождество является более общим понятием, чем равенство, поскольку оно справедливо для любых значений переменных.

Примером тождества может служить следующее выражение: x + y = y + x. Оно всегда истинно, независимо от значений x и y. Примером равенства может служить выражение x + 5 = 9, которое истинно только в том случае, если x равно 4.

Равенство: определение, примеры и особенности

Что такое равенство?

Равенство в математике – это понятие, означающее, что два выражения имеют одинаковое значение. Символ «=» используется для обозначения равенства.

Примеры равенства:

• 2 + 2 = 4
• 3x + 4 = 7
• y + 6 = 9

Равенство является одной из основных операций в математике и используется во всех ее разделах.

Особенности равенства:

• Равенство выполняется в обе стороны, то есть если два выражения равны, то их можно заменить друг на друга в любом выражении.
• Если к обоим частям равенства прибавить или вычесть одно и то же число, равенство сохранится.
• Если обе части равенства умножить или разделить на одно и то же число, равенство сохранится.

Знание равенства необходимо для решения многих математических задач и задач из других областей науки и техники.

Основные законы логики

Логика — это раздел философии. Он представляет собой науку о формах и законах правильного мышления. Закон логики — необходимая связь между логическими формами в процессе построения последовательного рассуждения. Цель его состоит в формулировании правил и рекомендаций, с помощью которых можно найти путь к истине. Это не законы самого окружающего мира, а правила мышления о нём.

Аристотель, который создал классификацию свойств бытия, всесторонне определяющих субъект, впервые сформулировал три из четырёх логических законов и подразумевал под этим предпосылку для объективной связи мыслей в процессе размышления. Основными в формальной логике считаются законы:

• тождества;
• исключённого третьего;
• непротиворечия;
• достаточного основания.

Тождественные преобразования выражений

Рассмотрим выражения \( x(y+7)\) и \( xy+7x.\) Вычислим их значения при \( x=9\) и \( y=-2\)

$$\tag{\textcolor{#3eb489}{1}} x(y+7)=9\cdot(-2+7)=45$$

$$xy+7x=9\cdot(-2)\tag{\textcolor{#3eb489}{2}}+7\cdot9=45$$

Мы видим что при \( x=9\) и \( y=-2\) соответственные значения выражений \( x(y+7)\) и \( xy+7x\) равны. Из распределительного и переместительного свойств умножения следует, что соответственные значения этих выражений равны при любых значениях переменных. О таких выражениях говорят, что они тождественно равны.

При решении уравнений, вычислении значений выражений и ряде других случаев одни выражения заменяют другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.

Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами. Мы уже встречались с тождественными преобразованиями выражений. К ним относятся, например, приведение подобных слагаемых, раскрытие скобок.

Пример 1. Приведем подобные слагаемые в сумме \(5x+2x-3x.\)

Чтобы привести подобные слагаемые, надо, как известно, сложить их коэффициенты и результат умножить на общую буквенную часть.

Имеем: $$5x+2x-3x=(5+2-3)x=4x$$
Выполненное преобразование основано на распределительном свойстве умножения.

Пример 2. Раскроем скобки выражения \(2a+(b-3c).\)

Воспользуемся правилом раскрытия скобок, перед которыми стоит знак “плюс”: если перед скобками стоит знак “плюс”, то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки.

Получим: $$2a+(b-3c)=2a+b-3c$$
Проведенное преобразование основано на сочетательном свойстве сложения.

Пример 3. Раскроем скобки в выражении \(a-(4b-c).\)

Применим правило раскрытия скобок, перед которыми стоит знак “минус”: если перед скобками стоит знак “минус”, то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки.

Получим: $$a-(4b-c)=a-4b+c$$

Выполненное преобразование также основано на свойствах действий над числами. Действительно, представим данное выражение в виде суммы:
$$a-(4b-c)=a+(-1)\cdot(4b-c)$$
Применим распределительное и сочетательное свойства умножения:

\

Примеры тождеств

Тождество нуля и единицы: это тождество утверждает, что любое число умноженное на 0 равно 0, а любое число умноженное на 1 равно этому числу. Например, 6 * 0 = 0 и 8 * 1 = 8.

Тождество остатка: в математике тождество остатка гласит, что если целое число a делится на число b, то его остаток равен 0, иначе oстаток будет меньше, чем b. Например, 18/3 = 6 и его остаток равен 0.

Тождество Паскаля: это формула, которая показывает, как каждое число в строке треугольника Паскаля является суммой двух чисел выше него в предыдущей строке. Например, в треугольнике Паскаля, третья строка содержит числа 1, 2, 1, и каждое число в строке равно сумме двух чисел выше него: 2 = 1 + 1.

Таблица истинности для тождеств:

A	B	A ∧ B	A ∨ B	A ⊕ B	A → B
1
1	1	1
1	1	1	1
1	1	1	1	1

Тождество в логике: это отношение между высказываниями, когда оба высказывания имеют одинаковую истинность для всех значений своих переменных.

Тождественно истинное высказывание: это высказывание, которое всегда истинно. Например, 1 + 1 = 2.

Что такое тождество?

Логично начать изложение материала с определения тождества
. В учебнике Макарычева Ю. Н. алгебра для 7 классов определение тождества дается так:

Определение.

Тождество
– это равенство, верное при любых значениях переменных; любое верное числовое равенство – это тоже тождество.

При этом автор сразу оговаривается, что в дальнейшем это определение будет уточнено. Это уточнение происходит в 8 классе, после знакомства с определением допустимых значений переменных и ОДЗ . Определение становится таким:

Определение.

Тождества
– это верные числовые равенства, а также равенства, которые верны при всех допустимых значениях входящих в них переменных.

Так почему, определяя тождество, в 7 классе мы говорим про любые значения переменных, а в 8 классе начинаем говорить про значения переменных из их ОДЗ? До 8 класса работа ведется исключительно с целыми выражениями (в частности, с одночленами и многочленами), а они имеют смысл для любых значений входящих в них переменных. Поэтому в 7 классе мы и говорим, что тождество – это равенство, верное при любых значениях переменных. А в 8 классе появляются выражения, которые уже имеют смысл не для всех значений переменных, а только для значений из их ОДЗ. Поэтому тождествами мы начинаем называть равенства, верные при всех допустимых значениях переменных.

Итак, тождество – это частный случай равенства. То есть, любое тождество является равенством. Но не всякое равенство является тождеством, а только такое равенство, которое верно для любых значений переменных из их области допустимых значений.

Тождественно равные выражения: определение

Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:

Определение 1

Тождественно равными
друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.

Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.

Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.

Определение 2

Тождественно равные выражения
– это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.

Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.

Можно указать еще и такое определение:

Определение 3

Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.

Тождественно равные выражения: определение

Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:

Определение 1

Тождественно равными
друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.

Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.

Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.

Определение 2

Тождественно равные выражения
– это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.

Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.

Можно указать еще и такое определение:

Определение 3

Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.

Определение тождественных выражений

Тождественным выражением называется математическое выражение, которое всегда имеет одно и то же значение вне зависимости от значений переменных, входящих в это выражение. Иными словами, тождественное выражение всегда является истинным.

Тождественные выражения используются в математике для проведения логических рассуждений. В них необходимо пользоваться только тождественными выражениями, т.к. они позволяют строить логические цепочки, которые доказывают правильность или ошибку высказывания.

Примеры тождественных выражений:

• 1 + 1 = 2 — это тождественное выражение, т.к. вне зависимости от значений 1, оно всегда будет истинным.
• x + y = y + x — это также тождественное выражение, т.к. оно верно для любых значений переменных x и y.
• sin²(x) + cos²(x) = 1 — это тождественное выражение, которое называется тригонометрическим тождеством.

Тождественные выражения имеют большое значение в математическом анализе, так как они упрощают выполнение сложных доказательств и упрощают расчеты. Использование этих выражений позволяет строить более точные и последовательные доказательства, что в итоге приводит к более точным выводам.

Примеры тождественных выражений с логарифмами

1. Тождественное выражение для суммы логарифмов:

Если a и b — положительные числа, то:

log_b(a) + log_b(c) = log_b(ac)

Например, log₃(4) + log₃(5) = log₃(20)

2. Тождественное выражение для разности логарифмов:

Если a и b — положительные числа, то:

log_b(a) — log_b(c) = log_b(a/c)

Например, log₃(10) — log₃(5) = log₃(2)

3. Тождественное выражение для степени логарифма:

Если a и b — положительные числа, то:

log_b(an) = nlog_b(a)

Например, log₂(83) = 3log₂(8) = 3log₂(23) = 9

4. Тождественное выражение для произведения логарифмов:

Если a и b — положительные числа, то:

log_b(a)log_b(c) = log_b(ac)

Например, log₃(4)log₃(5) = log₃(20)

5. Тождественное выражение для деления логарифмов:

Если a и b — положительные числа, то:

log_b(a)/log_b(c) = log_a(c)

Например, log₅(100)/log₅(10) = log₁₀(100) = 2

Примеры равенств

Равенство — это математическое понятие, которое означает, что две величины или выражения равны. При этом мы можем использовать различные математические операции, чтобы получить результат, который подтверждает равенство.

Вот некоторые примеры равенств:

• 2 + 2 = 4 — это одно из самых простых примеров равенства. Два плюс два всегда будет равно четырем, независимо от того, как мы это считаем.
• x + 5 = 12 — это равенство с неизвестным значением x. Если мы вычтем 5 из обеих сторон, то получим x = 7.
• sin²(x) + cos²(x) = 1 — это равенство, которое используется в тригонометрии. Оно означает, что квадрат синуса и квадрат косинуса любого угла x всегда будут в сумме давать единицу.

Важно помнить, что равенство не обязательно означает, что величины или выражения выглядят одинаково. Например, x / 2 = 10 — это тоже равенство, хотя выражения слева и справа от знака равно выглядят совершенно по-разному

И да, не стоит путать равенство с тождеством. В этом разница заключается в том, что тождество верно для всех значений переменных, а равенство — только для конкретных значений.

Понятия «тождество» и «тождественное равенство»

Что такое тождество в алгебре?

Определение 2

Тождество в математике — это равенство, которое выполняется всегда или, другими словами, верно для всех наборов значений переменных.

Если два или более одинаковых выражения написать рядом друг с другом через знак «равно», мы получим тождественное сходство, т е тождество.

К этим же равенствам относятся коммутативный закон сложения $a+b =b + a$ и ассоциативный закон умножения $(ab) cdot c = a cdot (bc)$, поскольку они верны независимо от значения переменные $a,b,c$. Сокращенные формулы для разности квадратов, разности квадратов и суммы квадратов являются другими примерами идентичных уравнений.

Иногда тождествами называют не только выражения, содержащие некоторые переменные, но и все арифметически верные равенства вида $2+2=4$.

Никакое равенство, содержащее переменные, нельзя назвать тождеством. Например, равенство $y+5 = 7$ соблюдается только при $y= 2$, при любом другом значении $y$ оно не соблюдается и поэтому не может называться тождеством.

Определение тождества

Равенство, которое является верным при любом значении, входящей в него переменной, называется тождеством. Тождество, как и уравнение, имеет переменную — x, y или любую другую букву. Разница между тождеством и уравнением заключается в том, что уравнение имеет корень — то есть значение переменной, при которой выполняется данное равенство. А в тождестве равенство должно выполняться при любом значении переменной. То есть, равенство не всегда будет тождеством.

Например, выражение:

является уравнением, поскольку верно только при .

А равенство является и тождеством и уравнением, так как верно при любом значении переменной , и как решение уравнения —  — любое число.

Запомни
Тождественно равными называются два выражения, если соответственные значения их равны при любых значениях переменных.

Запомни
Тождественным преобразованием называется замена выражения тождественно равным ему выражением. Например, когда мы раскрываем скобки, то выражение заменяется тождественно ему равным.

Пример:  — это тождественное преобразование левой части выражения — получаем тождество.

Примеры простых тождественных выражений

Тождественные выражения — это математические выражения, которые истинны для любых значений переменных, которые содержатся в выражении. Простые тождественные выражения — это такие выражения, которые могут быть выражены с помощью одного уравнения. Рассмотрим несколько примеров простых тождественных выражений:

• x + y = y + x — данное уравнение иллюстрирует свойство коммутативности в сложении. Это значит, что порядок слагаемых не влияет на результат.
• x(y + z) = xy + xz — это уравнение иллюстрирует свойство дистрибутивности умножения на сложение. Это значит, что умножение на сумму равносильно умножению на каждый из этих элементов и последующему сложению результатов.
• x — x = 0 — это уравнение иллюстрирует свойство обратности. Это означает, что каждый элемент имеет свой обратный элемент, который, в сложении с исходным элементом, даст ноль.

Кроме того, существует и множество более сложных тождественных выражений, которые могут быть выражены с помощью нескольких уравнений, но их изучение — это уже более серьезная математика.

Словарь лингвистических терминов

Тождество

Соответствие звуков, морфем, слов и словосочетаний, имеющих общее происхождение. Генетическое тождество часто не представляет собой материального и семантического совпадения. Так, генетическое тождество звуков не означает их акустического и артикуляционного совпадения. В современных языках генетически тождественные звуки могут отличаться по своей акустической и артикуляционной природе. Например, и генетически родственные звуки, хотя – заднеязычный смычной, – переднеязычный щелевой. Названные звуки регулярно соответствуют друг другу в одних и тех же морфемах, различающихся тем, что после шел гласный непереднего ряда, а после – гласный переднего ряда: железо (рус.), gelezis (лит), gelsu (прусск.);

желтый (рус.), geltas (лит.), gelb (нем). Тождество в риторике
: один из топов определения, отношение термов которого указывает на их полную или частичную равнозначность: «Деньги есть деньги»;

установленная топом идентичность позволяет разводить его различные значения: «Деньги есть деньги, но здесь рубли, а там валюта».

Тождество: определение

Что такое тождество?

Тождество – это математическое выражение, в котором две стороны эквивалентны и принимают одно и то же значение при любых значениях переменных или элементов, входящих в это выражение.

Другими словами, тождество — это равенство, которое верно для любого значения переменных, которые входят в это выражение. Особенность тождества заключается в том, что обе стороны равны не только при определенных значениях переменных, но и при всех возможных значениях.

Тождество обозначается знаком «≡» и это означает, что левая и правая части выражения равны между собой при любых значениях переменных.

Пример: (a + b)² ≡ a² + 2ab + b²

Данное тождество гласит, что квадрат суммы a и b равен сумме квадратов a и b и удвоенного их произведения. Значения переменных a и b могут быть любыми числами и данное тождество останется верным при всех этих значениях.

Доказательство тождеств

Если в выражении \(\textcolor{#ed5fa6}{5(b-c)-3c}\) раскрыть скобки, а затем привести подобные слагаемые, то получится тождественно равное ему выражение \(\textcolor{#ed5fa6}{5b-8c.}\)

Равенство $$5(b-c)-3c=5b-8c$$

верно при любых значениях переменных. Такие равенства называют тождественными.

Свойства действий над числами также являются тождествами, приведем некоторые из них:

$$\tag{\textcolor{#3eb489}{1}} a+b=b+a$$
$$\tag{\textcolor{#ed5fa6}{2}} a(bc)=(ab)c$$
$$\tag{\textcolor{#3eb489}{3}} a\cdot1=a$$
$$\tag{\textcolor{#ed5fa6}{4}} a+(-a)=0$$
$$\tag{\textcolor{#3eb489}{5}} a(-b)=-ab$$
$$\tag{\textcolor{#ed5fa6}{6}} (-a)(-b)=ab$$

Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений.

Докажем, например, тождество
$$\tag{1} 7(2+b)-(14-b)=8b$$
Преобразуем левую часть равенства \((1):\)

\

В результате тождественных преобразований мы получили правую часть равенства \((1).\) Значит, это равенство есть тождество.

Для доказательства тождества иногда преобразуют каждую его часть. Докажем, например, тождество
$$\tag{2} d(c-a)+ab=a(b-d)+cd$$
Выполним преобразования:

\

Левая и правая части равенства \((2)\) тождественно равны одному и тому же выражению. Поэтому они тождественно равны между собой. Значит, равенство \((2)\) — тождество.

Не всякое равенство есть тождество. Так, равенство \(x+2=2x\) не является тождеством. Действительно, если бы это равенство было тождеством, то оно было бы верным при всех значениях \(x.\) Однако, например, при \(x=1\) это равенство не является верным. Значит, оно не является тождеством.

Практическое применение тождественных выражений

Тождественные выражения очень полезны в различных областях, включая математику, физику, механику, информатику и т.д. Эти выражения позволяют упрощать сложные уравнения и устранять ошибки в вычислениях.

В математике и физике тождественные выражения используются для упрощения и решения уравнений. Например, когда нужно решить систему линейных уравнений, можно применить метод Гаусса. Этот метод включает упрощение уравнений с помощью тождественных выражений.

В программировании тождественные выражения используются для проверки наличия ошибок в коде. Если два выражения равны, то программа работает правильно. Если два выражения не равны, то программа содержит ошибку.

Также тождественные выражения используются для оптимизации алгоритмов и ускорения работы программ. Если заменить одно выражение на другое, то можно упростить вычисления и сократить время выполнения программы.

В целом, тождественные выражения помогают заменять сложные выражения на более простые и ускорять вычисления. Это очень полезный инструмент для различных областей знаний и профессий.

Что такое тождественно равные выражения?

Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю. Н. Макарычев приведена такая формулировка:

Определение.

– это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, которым отвечают одинаковые значения, также называют тождественно равными.

Это определение используется вплоть до 8 класса, оно справедливо для целых выражений , так как они имеют смысл для любых значений входящих в них переменных. А в 8 классе определение тождественно равных выражений уточняется. Поясним, с чем это связано.

В 8 классе начинается изучение других видов выражений, которые, в отличие от целых выражений, при некоторых значениях переменных могут не иметь смысла. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также области допустимых значений ОДЗ переменной, и как следствие — внести уточнение в определение тождественно равных выражений.

Определение.

Два выражения, значения которых равны при всех допустимых значениях входящих в них переменных, называются тождественно равными выражениями
. Два числовых выражения, имеющие одинаковые значения, также называются тождественно равными.

В данном определении тождественно равных выражений стоит уточнить смысл фразы «при всех допустимых значениях входящих в них переменных». Она подразумевает все такие значения переменных, при которых одновременно имеют смысл оба тождественно равных выражения. Эту мысль разъясним в следующем пункте, рассмотрев примеры.

Определение тождественно равных выражений в учебнике Мордковича А. Г. дается немного иначе:

Определение.

Тождественно равные выражения
– это выражения, стоящие в левой и правой частях тождества.

По смыслу это и предыдущее определения совпадают.

Философский словарь (Конт-Спонвиль)

Тождество

Тождество

Identité

Совпадение, свойство быть таким же. Таким же, как что? Таким же, как такое же, иначе это будет уже не тождество. Таким образом, тождество есть в первую очередь отношение себя к себе (мое тождество это и есть я сам) либо, если речь идет не о субъектах, отношение между двумя объектами, являющими собой один и тот же объект. «В строгом смысле слова этот термин чрезвычайно точен, – отмечает Кин, – вещь тождественна самой себе и ничему другому, даже дубликату-близнецу» («Сущности», статья «Тождество»). Два монозиготных близнеца, даже если предположить, что они совершенно схожи, являются близнецами только потому, что они суть два разных индивидуума; если бы они были абсолютно тождественны (в том смысле, в каком автор «Пармской обители» тождественен автору «Люсьена Левена» (и тот и другой романы принадлежат перу Стендаля. – Прим. ред.)), они составляли бы единое существо и не были бы близнецами. Таким образом, тождество в строгом смысле слова подразумевает уникальность, свойство быть одним и тем же, а никто не может в точности повторять никого, кроме себя.

В более широком и более прочно укоренившемся в традиции значении тождественными называют два объекта, дабы подчеркнуть их сходство. Например, друзья отмечают между собой тождество точек зрения или вкусов.

Оба значения имеют право на существование, важно лишь не путать одно с другим. Поэтому, употребляя слово «тождество» в первом значении, к нему часто добавляют определение «количественное» (чтобы подчеркнуть, что речь идет об одном и том же объекте: «Мы живем в одном и том же доме»)

В отличие от этого специфическое или качественное тождество указывает на полное сходство между многими различными объектами (выражение «У нас с ним одна и та же машина» подразумевает существование двух автомобилей одной марки, одной модели и одного цвета).

Тождество последнего вида никогда не бывает абсолютным (два тождественных автомобиля никогда не бывают абсолютно одинаковыми). Но бывает ли абсолютным количественное тождество? В настоящем времени – да, бывает, но только и исключительно в настоящем времени. Если рассматривать его с точки зрения времени, то оно становится таким же относительным, как качественное тождество, а быть может, и еще более иллюзорным. Стендаль начал писать «Люсьена Левена» в 1834 году и был тогда на четыре года моложе автора «Пармской обители». Какое же здесь тождество? А если он все-таки был тождественен себе более позднему, то почему написал другую книгу, а не ту же самую?

Заблуждением было бы думать, что понятие тождества, формальное по своей сути, способно дать нам какое-либо знание о реальной действительности. Утверждение, что Стендаль, Анри Бейль и автор «Жизни Анри Брюлара» являют собой единое целое, позволяет нам получить хоть какое-то знание только в том случае, если нам известно, что означает каждое из этих слов. Точнее даже, лишь потому, что это нам известно, мы и можем утверждать, что все три упомянутых лица являются одним и тем же человеком. Тождество, подобно удостоверению личности, ничего не сообщает о содержании того, на что указывает (ибо это не сущность); оно лишь говорит, что это содержание равно самому себе. А=А. Тождество не есть сущность, хотя сущность подразумевает тождество.

Вполне вероятно, во всяком случае, я придерживаюсь именно такого мнения, что во времени ничто не способно оставаться тождественным себе. Ничто не остается постоянным, как говорят буддисты, и нельзя дважды войти в одну и ту же реку. Что нисколько не мешает реальной действительности оставаться тождественной себе в настоящем времени. В этом пункте Парменид торжествует победу над Гераклитом, хотя триумф его тщетен: он побеждает и в том случае, если бы прав был Гераклит. Мы можем думать, что есть такая вещь, как тождество; однако о том, что такое тождество, мысль может узнать только благодаря бытию, а не самому тождеству. Не бывает онтологии a priori. Тождество есть необходимое, но пустое понятие. Это всего лишь имя, которое мы присваиваем чистому присутствию себя в реальности, тогда как реальность именем не является.

Тождество – одно из измерений молчания, благодаря которому возможна речь.

Основные равносильности алгебры высказываний

С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:

Коммутативность конъюнкции и коммутативность дизъюнкции

Коммутативность – это перестановочность:

Знакомые с 1-го класса правила: «От перестановки множителей (слагаемых) произведение (сумма) не меняется». Но при всей кажущейся элементарности этого свойства, справедливо оно далеко не всегда, в частности, некоммутативным является умножение матриц (в общем случае их  переставлять нельзя), а векторное произведение векторов – антикоммутативно (перестановка векторов влечёт за собой смену знака).

И, кроме того, здесь я снова хочу подчеркнуть формализм математической логики. Так, например, фразы «Студент сдал экзамен и выпил» и «Студент выпил и сдал экзамен» различны с содержательной точки зрения, но неразличимы с позиций формальной истинности. …Таких студентов знает каждый из нас, и из этических соображений мы не будет озвучивать конкретных имён =)

Ассоциативность логического умножения и сложения

Дистрибутивные свойства

Обратите внимание, что во 2-м случае будет некорректно говорить о «раскрытии скобок», в известном смысле здесь «фикция» – ведь их можно убрать вообще: , т.к. умножение – это более сильная операция

И опять же – эти, казалось бы, «банальные» свойства выполняются далеко не во всех алгебраических системах, и, более того, требуют доказательства (о которых мы очень скоро поговорим). К слову, второй дистрибутивный закон несправедлив даже в нашей «обычной» алгебре. И в самом деле:

Закон идемпотентности

Что делать, латынь….

Прямо какой-то принцип здоровой психики: «я и я – это я», «я или я – это тоже я» =)

И тут же несколько похожих тождеств:

…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)

Закон двойного отрицания

Ну а здесь уже напрашивается пример с русским языком – все прекрасно знают, что две частицы «не» означают «да». А для того, чтобы усилить эмоциональную окраску отрицания нередко используют три «не»: – даже с крохотным доказательством получилось!

 – «а был ли мальчик?» =)

В правом тождестве скобки можно опустить.

Законы де Моргана

Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если  – Студент ответил на 1-й вопрос и  – Студент ответил на 2-й вопрос. Тогда высказывание , гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению  – Студент не ответил на 1-й вопрос или на 2-й вопрос.

Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.

Докажем тождество . Поскольку в  него входит единственное высказывание , то «на входе» возможно всего лишь два варианта: единица либо ноль. Далее приписываем единичный столбец и применяем к ним правило И:
В результате «на выходе» получена формула, истинность которой совпадает с истинностью высказывания . Равносильность  доказана.

Да, это доказательство является примитивным (а кто-то скажет, что и «тупым»), но типичный Преподаватель по матлогике вытрясет за него душу. Поэтому даже к таким простым вещам не стОит относиться пренебрежительно.

Теперь убедимся, например, в справедливости закона де Моргана .

Сначала составим таблицу истинности для левой части. Поскольку дизъюнкция находится в скобках, то в первую очередь выполняем именно её, после чего отрицаем столбец  :
Далее составим таблицу истинности для правой части . Здесь тоже всё прозрачно – в первую очередь проводим более «сильные» отрицания, затем применяем к столбцам  правило И:
Результаты совпали, таким образом, тождество  доказано.

Любую равносильность  можно представить в виде тождественно истинной формулы . Это значит, что ПРИ ЛЮБОМ исходном наборе нулей и единиц «на выходе» получается строго единица. И этому есть очень простое объяснение: так как таблицы истинности  и  совпадают, то, разумеется, они эквивалентны. Соединим, например, эквиваленцией левую и правую часть только что доказанного тождества де Моргана: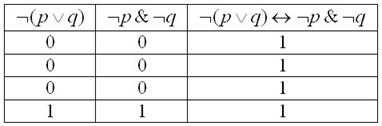
Или, если компактнее:

Задание 2

Доказать следующие равносильности:

а) ;

б)

Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!