Трапеция и ее свойства с определением и примерами решения

6. Решение задач по теме «Параллелограмм»

На про­шлом уроке мы уже рас­смот­ре­ли ряд задач, свя­зан­ных с па­рал­ле­ло­грам­мом и тра­пе­ци­ей. На этом уроке про­дол­жим ре­шать раз­лич­ные при­ме­ры на эту тему.

При­мер 1.

Пе­ри­метр па­рал­ле­ло­грам­ма  равен , . Какую сто­ро­ну па­рал­ле­ло­грам­ма пе­ре­се­ка­ет бис­сек­три­са угла? Найти от­рез­ки, ко­то­рые об­ра­зу­ют­ся при этом пе­ре­се­че­нии.

Дано:  – па­рал­ле­ло­грамм; ,  – бис­сек­три­са .

Ре­ше­ние:

Рис. 1

Пусть . Вос­поль­зу­ем­ся тем фак­том, что пе­ри­метр па­рал­ле­ло­грам­ма равен . Тогда: .

Как же вы­яс­нить: какую сто­ро­ну пе­ре­се­чёт бис­сек­три­са ?

Для этого вос­поль­зу­ем­ся сле­ду­ю­щи­ми рас­суж­де­ни­я­ми. Пусть бис­сек­три­са  пе­ре­се­ка­ет сто­ро­ну  (или её про­дол­же­ние) в точке . Тогда:  (по опре­де­ле­нию бис­сек­три­сы),  (свой­ство внут­рен­них од­но­сто­рон­них углов при па­рал­лель­ных пря­мых). От­сю­да:  – рав­но­бед­рен­ный. Зна­чит, . Зна­чит, .

Мы прак­ти­че­ски от­ве­ти­ли и на вто­рой во­прос за­да­чи: .

Ответ: бис­сек­три­са  пе­ре­се­ка­ет сто­ро­ну  и делит её на от­рез­ки  и .

При­мер 2.

Сто­ро­ны па­рал­ле­ло­грам­ма равны . Бис­сек­три­сы двух углов, при­ле­га­ю­щих к боль­шей сто­роне, делят про­ти­во­по­лож­ную сто­ро­ну на три от­рез­ка. Най­ди­те эти от­рез­ки.

Дано:  – па­рал­ле­ло­грамм;  – бис­сек­три­сы.

Найти: 

Ре­ше­ние:

Рис. 2

Если вос­поль­зо­вать­ся ре­ше­ни­ем при­ме­ра 1, можно сразу сде­лать вывод, что тре­уголь­ни­ки  – рав­но­бед­рен­ные (так как , ). По­лу­ча­ем, что . Тогда: .

Ответ: .

При­мер 3.

Через про­из­воль­ную точку ос­но­ва­ния рав­но­бед­рен­но­го тре­уголь­ни­ка про­ве­де­ны две пря­мые, па­рал­лель­ные бо­ко­вым сто­ро­нам. До­ка­зать, что пе­ри­метр по­лу­чен­но­го че­ты­рёх­уголь­ни­ка равен сумме бо­ко­вых сто­рон тре­уголь­ни­ка.

Дано:  – рав­но­бед­рен­ный тре­уголь­ник (); .

До­ка­зать: 

До­ка­за­тель­ство:

Рис. 3

 – па­рал­ле­ло­грамм (по опре­де­ле­нию – так как: ). До­ка­жем, что тре­уголь­ни­ки  – рав­но­бед­рен­ные. Дей­стви­тель­но:  – как со­от­вет­ствен­ные. С дру­гой сто­ро­ны,  (свой­ство рав­но­бед­рен­но­го тре­уголь­ни­ка). Зна­чит,  и тре­уголь­ни­ки  – рав­но­бед­рен­ные. Тогда, , что и тре­бо­ва­лось до­ка­зать.

До­ка­за­но

Как найти среднюю линию трапецииДля равнобедренной фигуры

В случае, если базовая фигура – трапеция равнобедренная, приведенные выше формулы будут иметь следующий вид.

При наличии значений оснований трапеции изменений в выражении не произойдет.

l = (a+b)/2, a, b – основания, l – средняя линия.

Если известны высота, основание и углы, к нему прилегающие, то:

l=a-h*ctgα,
l=b+h*ctgα,

l – линия средины,
a, b – основания (b
α – углы при нем,
h – высота фигуры.

Если известна боковая сторона трапеции и одно из оснований, то определить искомую величину можно, обратившись к выражению:

l=a-√(c*c-h*h),
l=b+√(c*c-h*h),
l – линия средины,
a, b – основания (b
h – высота фигуры.

При известных значениях высоты, диагоналей (а они равны между собой) и углах, образованных в результате их пересечения, линию средины можно найти следующим образом:

l=(d*d)/2h*sinγ или l=(d*d)/2h*sinφ,

l – линия средины,
d – диагонали,
φ, γ – углы между ними,
h – высота фигуры.

Известны площадь и высота фигуры, тогда:

l=S/h,
S – площадь,
h – высота.

Если перпендикуляр-высота неизвестен, его можно определить с помощью определения тригонометрической функции.

h=c*sinα, поэтому
l=S/c*sinα,
l – линия средины,
S – площадь,
c – боковая сторона,
α- угол у основания.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Формулы, теоремы и свойства элементов треугольника. Справочник репетитора по математике

Теоретичесикие шпаргалки по элементарной геометрии для занятий с репетитором по математике. Базовый школьный уровень. Свойства элементов треугольника. В помощь для решению задач по всему курсу планиметрии. Для тренировки решения задач С4 на ЕГЭ по математике.

1) Определение тригонометрических функций острого угла в прямоугольном треугольнике и теорема ПифагораТеорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов, то есть

2) Формулы площади треугольника

• 3) Подобие треугольников
• Определение: два треугольника называются подобными, если у них соответствующие углы равны и соответствующие стороны пропорциональны, то есть
  и
• Обозначение:
• 4) Признаки подобия двух треугольников
• 1-й признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
• Коротко: если , то
• 2-й признак:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны
• Коротко: если и , то
• 3-й признак:если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны, то есть
• Коротко: если , то
• 5) Свойства подобных треугольников
• если , то
• , где
• и  — любые соответствующие медианы (проведенные к соответствующим сторонам)
• и  — любые соответствующие биссектрисы (проведенные к соответствующим сторонам)
• и  — любые соответствующие высоты (проведенные к соответствующим сторонам)
• 6) Подобие прямоугольных треугольников. Высота, проведенная из вершины прямого угла
• Теорема: высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:
• 7) Свойство медиан в треугольнике.
• Теорема 1: Все медианы треугольника пересекаются в одной точке (центр тяжести треугольника) и делятся этой точкой в отношении 2:1, считая от вершин. То есть
• Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),
• То есть
• Теорема 3: все три медианы делят треугольник на 6 равновеликих треугольников, то есть
• Свойство биссектрис в треугольнике Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.
• То есть

Теорема 2: Все биссектрисы в треугольнике пересекаются в одной точке, которая является центром вписанной с треугольник окружности. В любой треугольник можно вписать окружность и только одну.

9) Свойство точки пересечения серединных перпендикуляров к сторонам треугольника:

Теорема: все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке и эта точка является центром описанной около треугольника окружности. Вокруг любого треугольника можно описать окружность и только одну.

1. 10) Теорема о разделительном отрезке в треугольнике

   Теорема: Отрезок, соединяющий вершину треугольника с противоположной стороной делит ее на отрезки, пропорциональные площадям образованных треугольников.

2. То есть
3. 11) Средняя линия треугольника
4. Теорема: Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.
5. То есть и
6. 12) Теорема синусов и теорема косинусов
7. Теорема синусов: Cтороны треугольника пропорциональны синусам противолежащих углов и каждое отношение стороны к синусу равно диаметру описанной около треугольника окружности.
8. То есть
9. Теорема косинусов: Квадрат стороны треугольника равне сумме квадратов двух других сторон минус удвоенное произведение этих сторон на синус угла между ними, то есть
10. 13) Теорема Менелая

    Теорема: Произведение отношений отрезков, на которые произвольная прямая делит стороны треугольника (или их продолжения) равно единице

11. То есть

Комментарий репетитора по математике: несправедливо выброшенная теорема из школьного курса геометрии. Рекомендую репетиторам включить ее в подготовку, по крайней мере к вузовским олимпиадам и вступительным экзаменам по математике в МГУ. В программу ЕГЭ теорема Менелая не входит, но несколько типов задач без нее решаются очень сложно.

• 14) Теорема Чевы
• Теорема:если через вершины треугольника и произвольную внутреннюю точку провести отрезки к противоположным сторонам (чевианы), то их точки пересечения разделят стороны на отрезки, произведение отношений которых равно единице.
• То есть

Колпаков А.Н. Репетитор по математике.

Прямоугольная и равнобедренная трапеция

Существует два частных вида трапеции, обладающих особыми свойствами. Первый из них – это прямоугольная трапеция. Она отличается тем, что один из ее углов равен 90°.

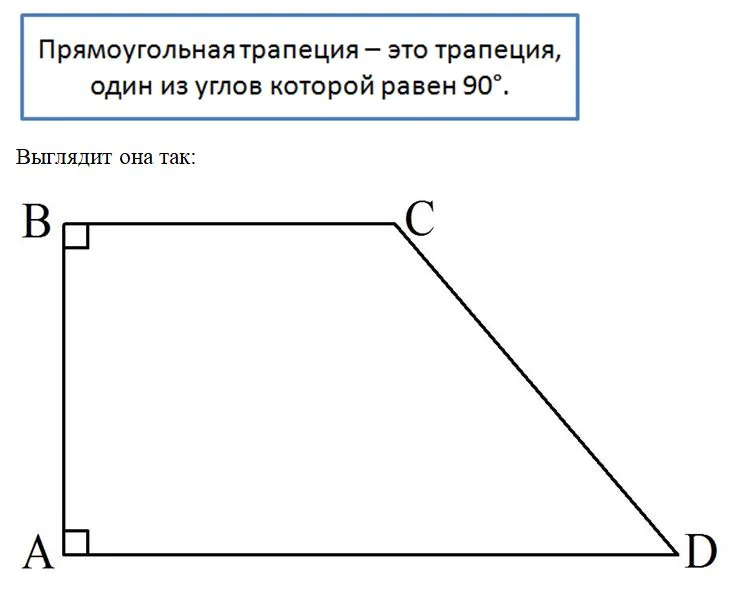
Здесь∠А = 90°. Легко догадаться, что на самом деле если у трапеции хоть один угол составляет 90°, то найдется и ещё один угол, также равный 90°. В данном случае это ∠В. Сумма ∠A и ∠D должна составлять 180°, ведь они односторонние. Именно поэтому из условия

Задание. Основания прямоугольной трапеции имеют длину 10 и 15 см, а один из углов составляет 45°. Вычислите длину ее наименьшей боковой стороны?

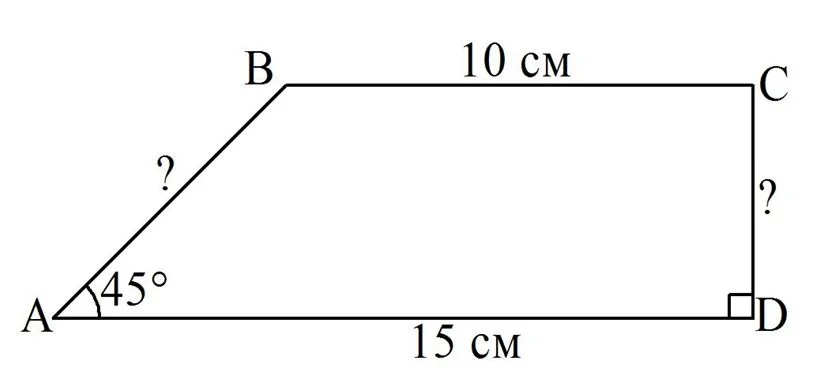
Решение:

Пусть основания заданной трапеции – это отрезки АD и ВС, ∠А = 45°, ∠D = ∠C = 90°. Опустим из точки В перпендикуляр ВН на АD:

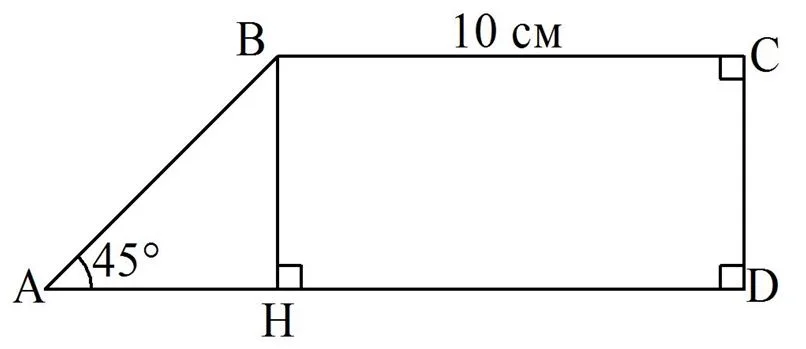
Очевидно, что ВН||CD, ведь эти отрезки перпендикулярны одной прямой АD. Получается, что в четырехуг-ке НВСD противоположные стороны попарно параллельны, то есть он является параллелограммом. Отсюда вытекает равенство его сторон:

Нашли СD, но является ли этот отрезок именно меньшей боковой стороной трапеции? Для ответа на этот вопрос вернемся к ∆АВН. В нем АВ – это гипотенуза, а потому она заведомо больше катета ВН, то есть больше 5 см. Значит, именно CD – это меньшая боковая сторона.

Ответ: 5 см.

Ещё один особый вид трапеции – равнобедренная трапеция. Она отличается тем, что у неё длины боковых сторон одинаковы.

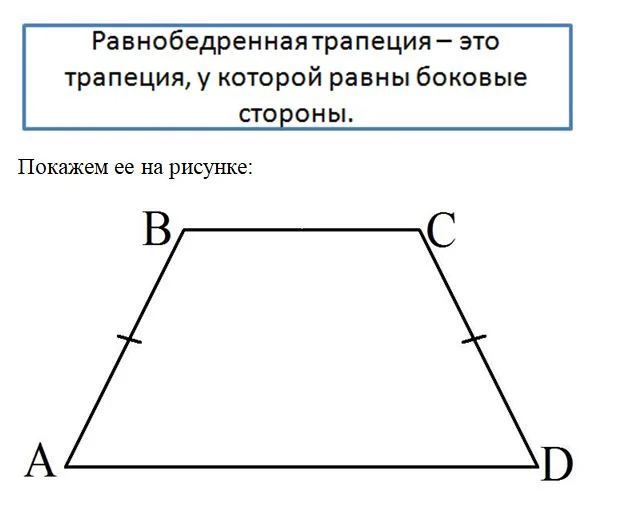
Равнобедренная трапеция обладает рядом интересных свойств. Начнем с того, что углы при каждом из ее оснований равны.

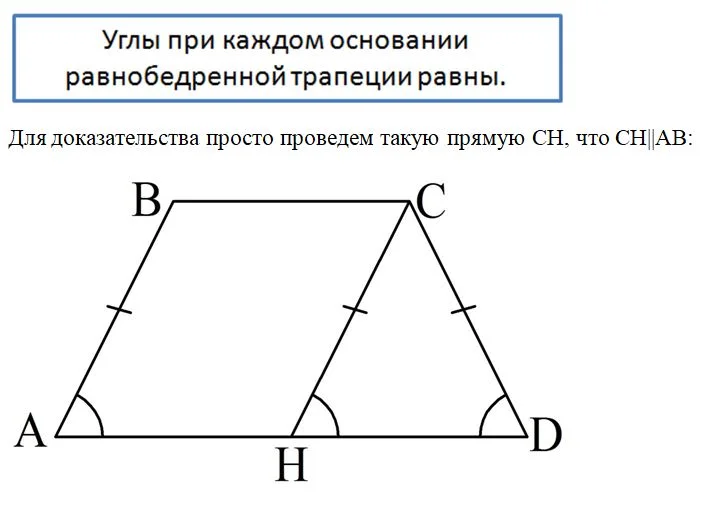
В итоге мы получили четырехуг-к АВСН, в котором АВ||CН, ВС||АН. Это значит, что он является параллелограммом, и тогда

Отсюда сразу же вытекает и второе свойство равнобедренной трапеции – у неё равные диагонали.

Доказывается этот факт с помощью :

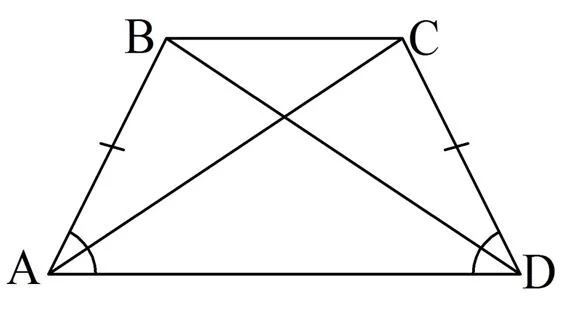
Действительно, треуг-ки ∆АВD и ∆АСD равны, ведь

Оказывается, есть признаки, которые позволяют определить, является ли трапеция равнобедренной. Сформулируем первый из них:

Для доказательства снова построим в трапеции АВСD такую прямую СН, что СН||АВ:

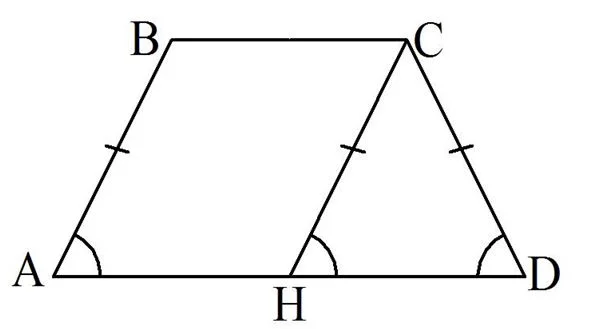
Тогда

Несколько сложнее доказать другую теорему:

Пусть в трапеции АВCD одинаковы диагонали ВD и АС. Для определенности будем считать, что большее основание – это АD. Опустим из точек В и С перпендикуляры ВЕ и СF на АD:

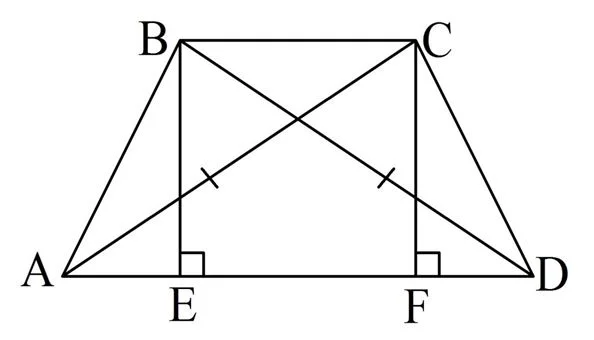
Ясно, что эти перпендикуляры параллельны друг другу, ведь они перпендикулярны третьей прямой. Тогда в ВСFЕ противоположные стороны параллельны, то есть эта фигура – параллелограмм. Отсюда вытекает, что

BE = CF

Далее рассмотрим ∆ВЕD и ∆АСF. Они оба являются прямоугольными, у них одинаковы гипотенузы (АС = ВD), а также и катеты ВЕ и СF. Значит, эти треуг-ки равны, следовательно,

Задание. Один из углов равнобедренной трапеции составляет 55°. Найдите все остальные углы этой трапеции.

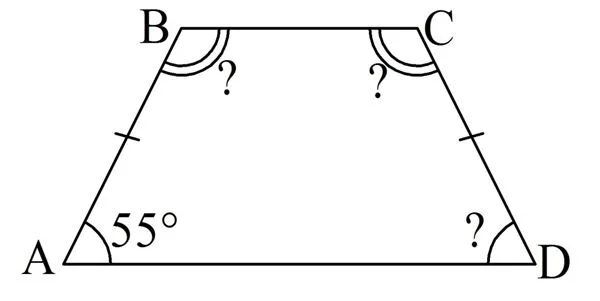
Решение. Проще всего найти ∠D, ведь углы при основании равнобедренной трапеции одинаковы:

Заметим одно важное обстоятельство. Если достроить равнобедренную трапецию до треугольника, продолжив ее боковые стороны, то получится равнобедренный треуг-к:

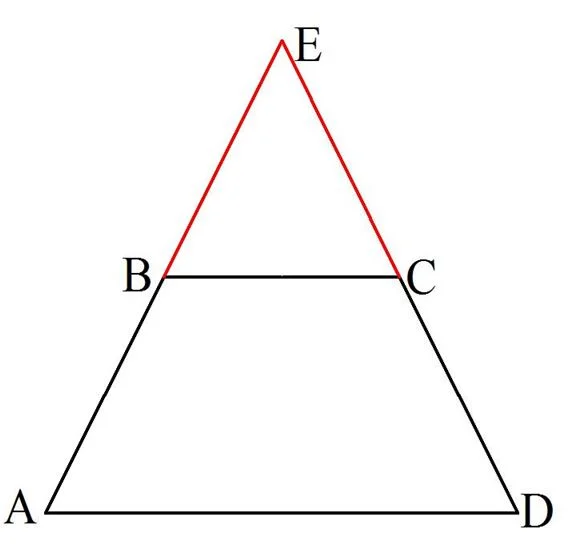
Действительно, если АВСD – равнобедренная трапеция, то

∠А = ∠D

Пусть продолжения боковых сторон пересеклись в некоторой точке Е. Тогда в ∆АЕD два угла, ∠А и ∠D, окажутся равными, следовательно, ∆АЕD– равнобедренный.

Формулы для нахождения длины средней линии для разных видов трапеции

Существует три вида трапеций, длину средней линии которых можно рассчитать по-разному, но можно и общими способами. До того, как рассмотреть конкретные формулы, рассмотрим какие виды трапеций бывают

Виды трапеций

Равнобедренная (или равнобокая) трапеция — это трапеция, у которой боковые стороны равны друг другу.

Прямоугольная трапеция — это трапеция, у которого оба угла при одной из боковых сторон прямые, то есть по 90 °.

Трапеция является разносторонней, если ее боковые стороны не равны, и ни один из углов при основании не является прямым.

Рассмотрим различные варианты нахождения длины средней линии. Большинство из представленных ниже формул можно использовать для любого вида трапеции, но в зависимости от того, что дано в задаче мы и можем выбирать какой формулой нам удобнее воспользоваться.

1. Нахождение длины средней линии трапеции через длины оснований.

Средняя линия в данном случае равно полусумме оснований трапеции (рис.9).

Формула 6

\(m\;=\;\frac{a+b}2\)

2. Длина средней линии через площадь и высоту трапеции (рис.10)

Формула 7

\(m\;=\;\frac Sh\), где S — площадь трапеции, а h — ее высота.

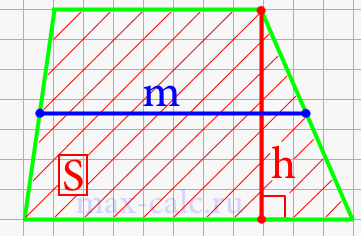
3. Длина средней линии через нижнее основание, высоту трапеции и углы при нижнем основании (рис.11)

Формула 8

\(m\;=a\;-\;h\ast\frac{(ctg\;\alpha\;+\;ctg\;\beta)}2\)

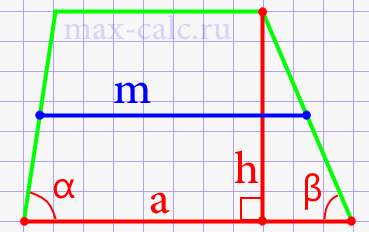
4. Способ нахождения длины средней линии через верхнее основание, высоту трапеции и углы при нижнем основании (рис.12)

Формула 9

\(m\;=b\;-\;h\ast\frac{(ctg\;\alpha\;+\;ctg\;\beta)}2\)

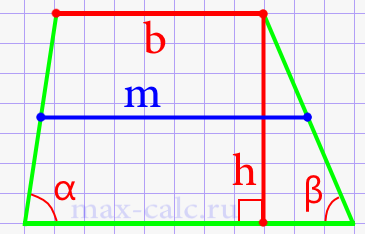
5. Способ нахождения длины средней линии через диагонали, высоту и угол между диагоналями трапеции.

Формула 10

\(m\;=\frac{D\ast d}{2h}\ast\sin\left(\alpha\right)\), где: D, d — диагонали, h — высота, sin α — угол между диагоналями

6. Средняя линия трапеции через боковые стороны, верхнее основание и углы при нижнем основании (рис.13).

Формула 11

\(m\;=\frac{2b\;+\;c\ast\cos\left(\alpha\right)\;+\;d\ast\cos\left(\beta\right)}2\)

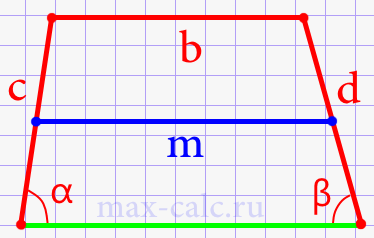
7. Средняя линия трапеции через боковые стороны, нижнее основание и углы при нижнем основании (рис.14).

Формула 12

\(m\;=\frac{2a\;-\;c\ast\cos\left(\alpha\right)\;-\;d\ast\cos\left(\beta\right)}2\)

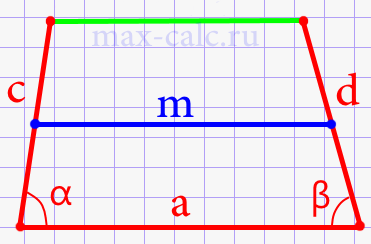
8. Средняя линия равнобедренной трапеции через боковую сторону, нижнее основание и угол между ними (рис.15).

Формула 13

\(m\;=\frac{2a\;-\;2c\ast\cos\left(\beta\right)}2\)

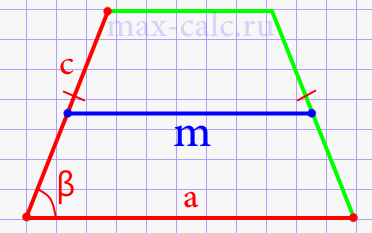
9. Средняя линия равнобедренной трапеции через боковую сторону, верхнее основание и угол при нижнем основании (рис.16)

Формула 14

\(m\;=\frac{2b\;+\;2c\ast\cos\left(\beta\right)}2\)

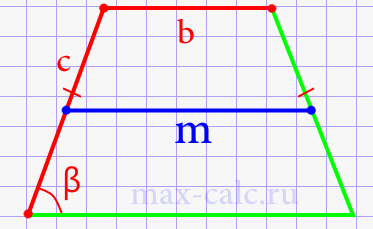
10. Средняя линия прямоугольной трапеции через нижнее основание, высоту и острый угол при нижнем основании.

Формула 15

\(m\;=a\;-h\ast\frac{ctg\;\beta}2\)

Определение медианы трапеции (средняя линия, средний сегмент)

Открытый справочник по математике

Главная
Контакт
О
Тематический указатель

Отрезок между серединами катетов трапеции Также известен как средняя линия или средний сегмент

Попробуйте это Перетащите оранжевые точки на каждой вершине
изменить форму трапеции

Обратите внимание на поведение красной срединной линии

Недвижимость

Срединная линия всегда параллельна основаниям. Отрегулируйте трапецию выше, перетащив любую вершину, и убедитесь, что это так.

Длина медианы равна средней длине оснований, или по формуле:

Если одно из оснований имеет нулевую длину, результатом будет треугольник.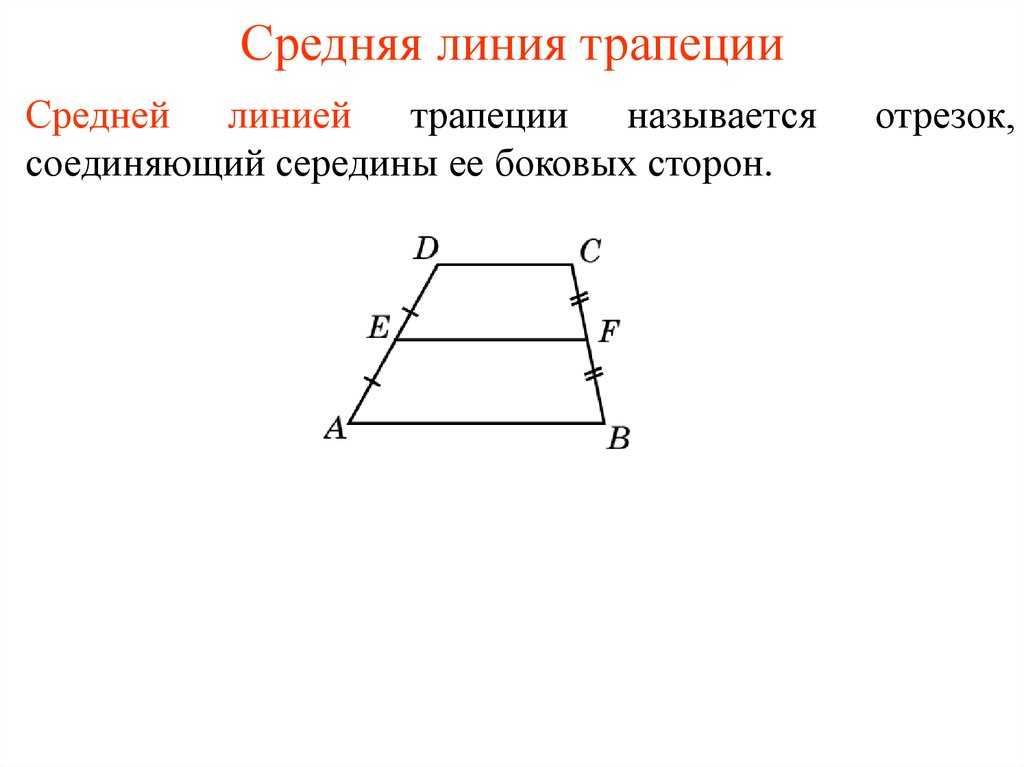

Средняя линия трапеции

Урок 10. Геометрия 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Конспект урока “Средняя линия трапеции”

Вспомним, какую фигуру называют трапецией.

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называют её основаниями, а две другие — боковыми сторонами.

Известны два частных случая трапеции. Равнобокая трапеция, у которой боковые стороны равны. И прямоугольная трапеция, у которой один из углов прямой.

К слову, у такой трапеции будет два прямых угла.

Повторив определение трапеции, введём понятие средней линии трапеции.

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Изобразим средние линии трапеций изображённых на рисунке.

Для этого сначала найдём их боковые стороны. Далее отметим точками их середины. Ну, а потом проведем средние линии.

Выполним задание. Пользуясь данными рисунков, указать пункты, в которых является средней линией трапеции .

На первом рисунке точка М не является серединой боковой стороны AB, поэтому МN не является средней линией трапеции.

На втором рисунке точки М и N — середины сторон BC и AD, но они являются основаниями трапеции. А по определению средняя линия трапеции соединяет середины боковых сторон. Значит, в данном случае МN не является средней линией.

На третьем рисунке видим, что точки М и N — середины боковых сторон. Причём по рисунку понятно, что эта трапеция — равнобокая.

Так получаем, что МN в данном случае — средняя линия трапеции ABCD.

Посмотрев на следующий рисунок, не трудно заметить, что МN соединяет середину одного из оснований и середину одной из боковых сторон, а не середины боковых сторон. Поэтому МN не является средней линией.

На рисунке под номером 5 точки М и N середины боковых сторон АB и CD трапеции ABCD. Значит, МN — её средняя линия.

В последнем случае точки М и N не поровну делят боковые стороны трапеции, поэтому МN не является её средней линией.

Мы получили, что только на рисунках под номерами 3 и 5 изображены средние линии трапеции.

Как и средняя линия треугольника, средняя линия трапеции обладает определёнными свойствами.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

1.

2.

Что и требовалось доказать.

Выполним задание, где, пользуясь этой теоремой и данными рисунков, найдём длины средних линий трапеций.

Длина средней линии трапеции равна полусумме оснований.

На рисунке а известны длины оснований. Поэтому не составит никакого труда найти, что .

Перейдём к рисунку б.

Известен периметр трапеции, тогда можем записать,

.

В последнем случае также дан периметр трапеции и известны боковые стороны.

Записав периметр через стороны, и, подставив известные значения, можем выразить сумму оснований.

Задача. В трапеции найти длины оснований и , если в два раза больше и длина средней линии равна .

Ответ: мм, мм.

Задача. В прямоугольной трапеции . Найти длину средней линии , если , а угол .

1.

2.

3.

4.

5.

Ответ: .

Подведём итоги нашего урока.

Сегодня мы познакомились с понятием средней линии трапеции. Это отрезок, соединяющий середины её боковых сторон.

При этом мы выяснили, что средняя линия трапеции обладает следующими свойствами: она параллельна основаниям трапеции и равна их полусумме.

Так же мы рассмотрели примеры применения этих знаний при решении задач.

Примеры задач

№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.

Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).

Теперь нужно воспользоваться подходящей формулой для площади:

S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм2). Задача решена.

Ответ: площадь трапеции равна 4,5 дм2.

№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.

Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.

Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.

Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.

Таким образом, площадь трапеции равна 5 * 4 = 20 см2.

Ответ: S = 20 см2.

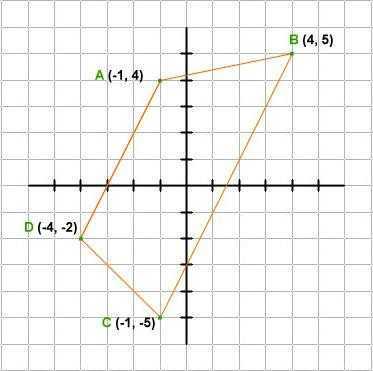
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.

Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).

Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.

S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см2).

Ответ: Искомая площадь равна 45 см2.

№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.

Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.

Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н₁, большей АОЕД — н₂.

Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:

(х + а₂) * н₁ = 1/5 (х + а₁) * н₂

или

н₁ /н₂ = (х + а₁) / (5(х + а₂)).

Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:

н₁ /н₂ = (х — а₂) / (а₁ — х).

В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а₁) / (5(х + а₂)) равно (х — а₂) / (а₁ — х).

Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.

В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.

Ответ: х = √ {(а₁ 2 + 5 а₂ 2 ) / 6}.

Свойства подобия

Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.

Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.

Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.

Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).

Основные понятия

Рисунок 1. Классическая форма трапеции.

Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые параллельны друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).

Если сложить все градусные меры внутренних углов, то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.

Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Примеры задач на понятие средней линии трапеции

Пример 1

Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.

Решение.

Обозначим среднюю линию трапеции через $n$.

Сумма боковых сторон равна

Следовательно, так как периметр равен $52\ см$, сумма оснований равна

Значит, по теореме 1, получаем

Ответ:
$10\ см$.

Пример 2

Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.

Решение.

Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).

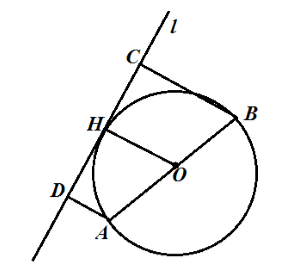
Рисунок 2.

Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем

Средняя линия трапеции равна полусумме
оснований. Она соединяет середины боковых сторон трапеции и всегда параллельна основаниям.

Если основания трапеции равны a и b, то средняя линия m равна
m=(a+b)/2.

Если известна площадь трапеции, то среднюю линию можно найти
и другим способом, разделив площадь трапеции S на высоту трапеции h:

То есть, средняя линия трапеции
m=S/h

Способов найти длину средней линии трапеции много. Выбор способа зависит от исходных данных.

Вот формулы длины средней линии трапеции
:

Чтобы найти среднюю линию трапеции, можно воспользоваться одной из пяти формул (выписывать их не буду, так как они уже есть в других ответах), но это только в тех случаях, когда известны нужные нам значения исходных данных.

На практике приходится решать много задач, когда данных недостаточно, а нужный размер нужно все таки найти.

Здесь есть такие варианты

пошаговым решением подвести все таки под формулу;

используя другие формулы, составить и решить необходимые уравнения.

нахождения длины середины трапеции методом подвода под нужную нам формулу
с помощью других знаний о геометрии и применяя при этом алгебраические уравнения:

Имеем равнобедренную трапецию, ее диагонали пересекаются под прямым углом, высота равна 9 см.

Делаем рисунок и видим, что в лоб эту задачу не решить (недостаточно данных)

Поэтому мы немного упростим и проведем высоту через точку пересечения диагоналей.

Это первый важный шаг, который ведет к быстрому решению.

обозначим высоту двумя неизвестными, увидим нужные нам равнобедренные треугольники со сторонами х
и у

и уже легко найдем сумму оснований
трапеции

она равна 2х+2у

И вот только теперь мы можем применить формулу где

и равна она х+у
а по условию задачи это длина высоты равная 9 см
.

И вот теперь мы вывели несколько моментов для равнобедренной трапеции, диагонали которой пересекаются под прямым углом

в таких трапециях

средняя линия всегда равна высоте

площадь всегда равна квадрату высоты
.

Средняя линия трапеции это отрезок, который соединяет середины боковых сторон трапеции.

Среднюю линию любой трапеции несложно найти, если пользоваться формулой:

m = (a + b)/2

m длина средней линии трапеции;

a, b длины оснований трапеции.

Итак, длина средней линии трапеции равна полусумме длин оснований
.

Основная формула для формулы средней линии трапеции:длина средней линии трапеции равна полусумме е оснований a и b: MN=(a+b)2.Доказательством этой формулы служит формула для средней линии треугольника.Любая трапеция может быть представлена после того как проведены из концов меньшего основания высоты на большее основание.Рассматриваются 2 полученных треугольника,и прямоугольник.После этого легко доказывается формула для средней линии трапеции.

Чтобы найти среднюю линию трапеции нам нужно знать величины оснований.

После того,как нашли эти величины или может быть они нам были известны,то складываем эти числа и просто делим пополам.

Это и будет средняя линия трапеции
.

Насколько я помню уроки школьной геометрии, для того, чтобы найти длину средней линии трапеции, нужно сложить длины оснований и разделить на два. Таким образом длина средней линии трапеции, равна полусумме оснований.

Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.