Как найти периметр ромба? ответ на

Основные сведения о фигуре ромб

Рассмотрим особый вид параллелограмма, для которого характерны следующие признаки:

1. Две стороны, являющиеся смежными, равны по величине.
2. Проведенные из углов диагонали пересекаются в центре фигуры таким образом, что образуют прямой угол.
3. Определенная диагональ разделяет углы, которые она соединяет, пополам.

По этим признакам можно четко определить, когда параллелограмм является ромбом.

Ромбом называется геометрическая фигура, которая является параллелограммом и имеет все четыре стороны равной длины.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Произошло название от греческого слова ῥόμβος либо латинского rombus. В переводе они означают «бубен».

При этом геометрическими свойствами ромба являются:

1. Поскольку ромб — параллелограмм, его стороны, лежащие противоположно, имеют равные величины и попарную параллельность. Кроме этого, для всех ромбов характерно равенство противоположных углов, а также факт, что соседние с ними углы составляют в сумме 180о.
2. С помощью проведения диагоналей можно разделить ромб на четыре треугольника, имеющих прямые углы. При этом диагонали пересекутся в центре фигуры в точке, которая разделит их пополам.
3. Вышеуказанные диагонали будут биссектрисами углов ромба.
4. Если длину диагоналей возвести в квадрат и сложить эти квадраты, то получишь квадрат стороны, увеличенный в 4 раза (данное свойство вытекает из тождества параллелограмма).
5. В ромб можно вписать прямоугольник, при этом его углы будут располагаться на серединах его сторон.
6. Оси симметрии ромба обязательно будут перпендикулярны диагоналям ромба.
7. Кроме прямоугольника в ромб можно вписать окружность. Ее центр будет совпадать с точкой, в которой пересекаются диагонали.

Зная вышеизложенные свойства, легко проводить вычисления величин, характеризующих данный ромб и строить внутри него геометрические фигуры.

Понятие периметра ромба

Периметр любой плоской геометрической фигуры составляет сумму длин его границ. Ромб не является исключением.

Исходя из определения, единицы измерения периметра аналогичны единицам длины.

Однако найти периметр ромба можно не только сложив длины всех четырех сторон. В геометрии существует еще один метод, который детально будет рассмотрен ниже.

Формула площади ромба

Математика играет ключевую роль в вашем высшем образовании и на вступительных экзаменах. Будь то вступительные экзамены или школьные экзамены, знание математики необходимо для достижения успеха в своих амбициях. Одной из таких тем из главы «Площадь и периметр» является вычисление площади ромба.

В евклидовой геометрии ромбом называется четырехугольник, имеющий четыре ребра и четыре угла, причем все четыре ребра имеют одинаковую длину.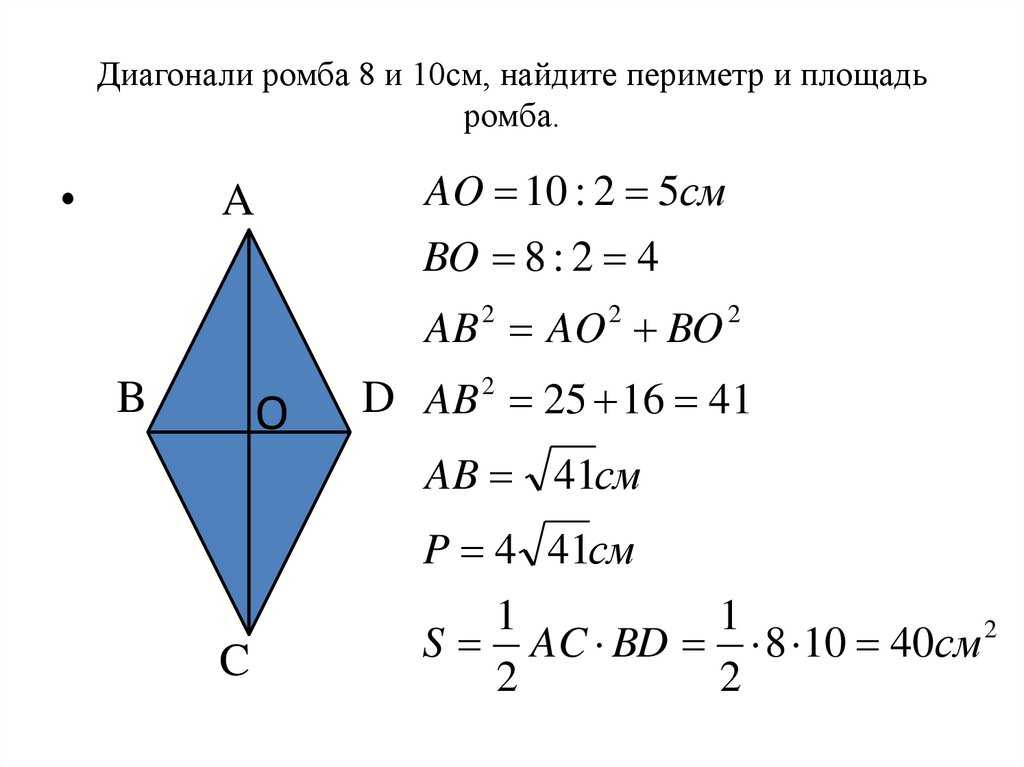

Формула вычисления площади и периметра ромба

Три способа вычисления площади ромба: диагональ, пол и высота и тригонометрия. Вот некоторые важные свойства алмаза:

Все стороны имеют одинаковую длину. Другая сторона также параллельна друг другу. Высота – это расстояние по вертикали между двумя параллельными сторонами. Две диагонали ромба делятся пополам под углом 90 градусов. Формула длины окружности бриллианта вычисляется очень легко. То есть длина окружности или P = 4 × a. Где «а» — длина одной стороны ромба. Диагональ ромба: 9 0003

 В диагональном методе площадь ромба можно рассчитать по следующей формуле: 

 A = ½ × d1 × d2.

Wo,

A = площадь алмаза. d1 =

Длина диагонали d1.

 d2 =

Длина диагонали d2.

 Если доступны какие-либо из этих значений, можно также рассчитать площадь и окружность бриллианта. Другими словами, зная площадь, можно вычислить и периметр. Возможен и обратный метод.

Как найти площадь ромба?

Площадь ромба можно получить тремя способами:

1. Используя диагонали – A = ½ × d1 × d2.

2. Использование базы и высоты – A = b × h.

3. С помощью тригонометрии – A = b2 × Sin(a).

 Где

Нахождение периметра прямоугольника

Определение

Прямоугольник – это геометрическая фигура, которая может быть квадратом, прямоугольником или же ромбом.

Характеристики:

1. У прямоугольника все углы по 90°
2. В отличие от квадрата, у прямоугольника равны только противолежащие стороны, которые являются его шириной и высотой. Эти стороны параллельны. Из этого следует, что каждый квадрат – прямоугольник, но квадратом являются не все прямоугольники.
3. Его прилегающие стороны перпендикулярны во всех случаях.
4. Если провести диагональ, то она поделит прямоугольник на два равных прямоугольных треугольника.
5. Если мы имеем две диагонали, то можно утверждать, что они одинаковой длины.

Прямоугольник

Периметр прямоугольника – это сумма длин всех его сторон. Получается, чтобы найти его периметр, воспользуемся формулами, в которых a – ширина и b – высота:

\

\

\

Пример 1

Найдите периметр прямоугольника, стороны которого равны 8 и 4 см.

Решение:

Воспользуемся формулой и подставим числа:

P = a + a + b + b

8 + 8 + 4 + 4 = 24 (см)

Ответ: периметр этого прямоугольника равен 24 см.

Пример 2

Найдите периметр прямоугольника, стороны которого равны 10 и 12 см.

Решение:

Теперь используем вторую формулу и подставим числа:

P = 2(a + b)

2(10 + 12) = 44 (см)

Ответ: периметр равен 44 см.

Пример 3

Найдите периметр прямоугольника, стороны которого равны 9 и 7.

Решение:

На очереди третья формула. Подставим числа и решим:

P = 2a + 2b

2 × 9 + 2 × 7 = 32 (см)

Ответ: периметр равняется 32 см.

Как найти периметр ромба: формула через стороны, диагонали

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение периметра ромба: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.

• Формула вычисления периметра
• Примеры задач

Формула вычисления периметра

1. По длине стороны

Периметр (P) ромба равняется сумме длин всех его сторон.

P = a + a + a + a

Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):

P = 4*a

2.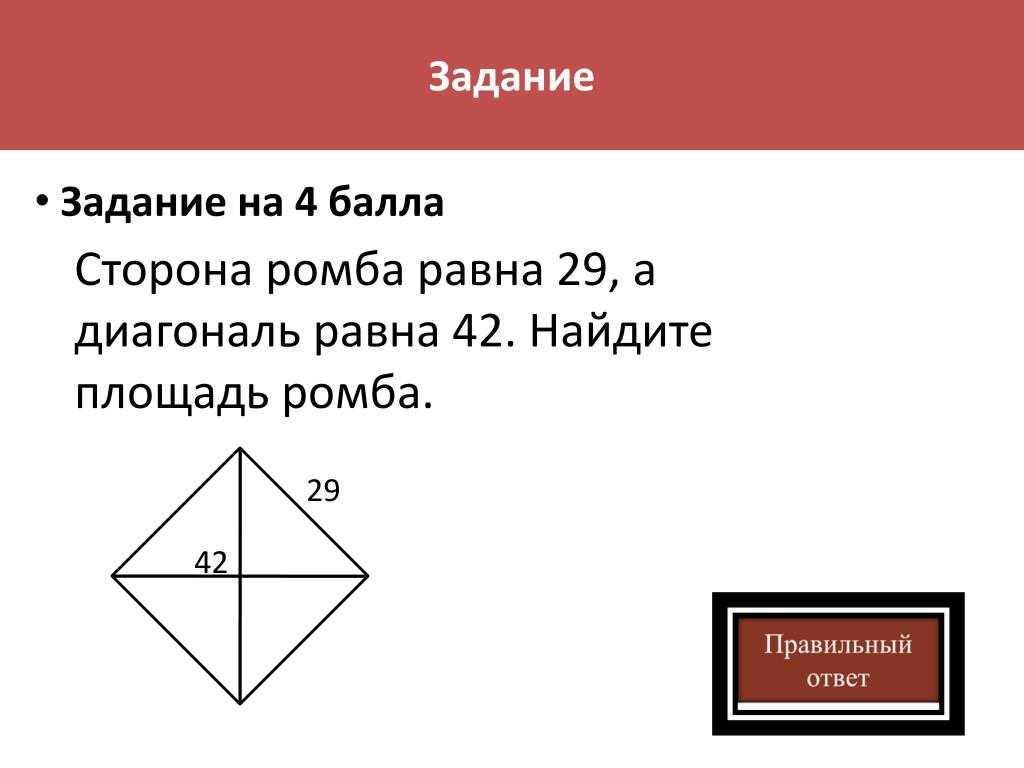 По длине диагоналей

Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:

• AO=OC=d₁/2
• BO=OD=d₂/2

Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.

Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:

AB2 = AO2 + OB2

Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:

AB2 = (d₁/2)2 + (d₂/2)2, или

Таким образом, периметр равняется:

Примеры задач

Задание 1Найдите периметр ромба, если длина его стороны составляет 7 см.

Решение:Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.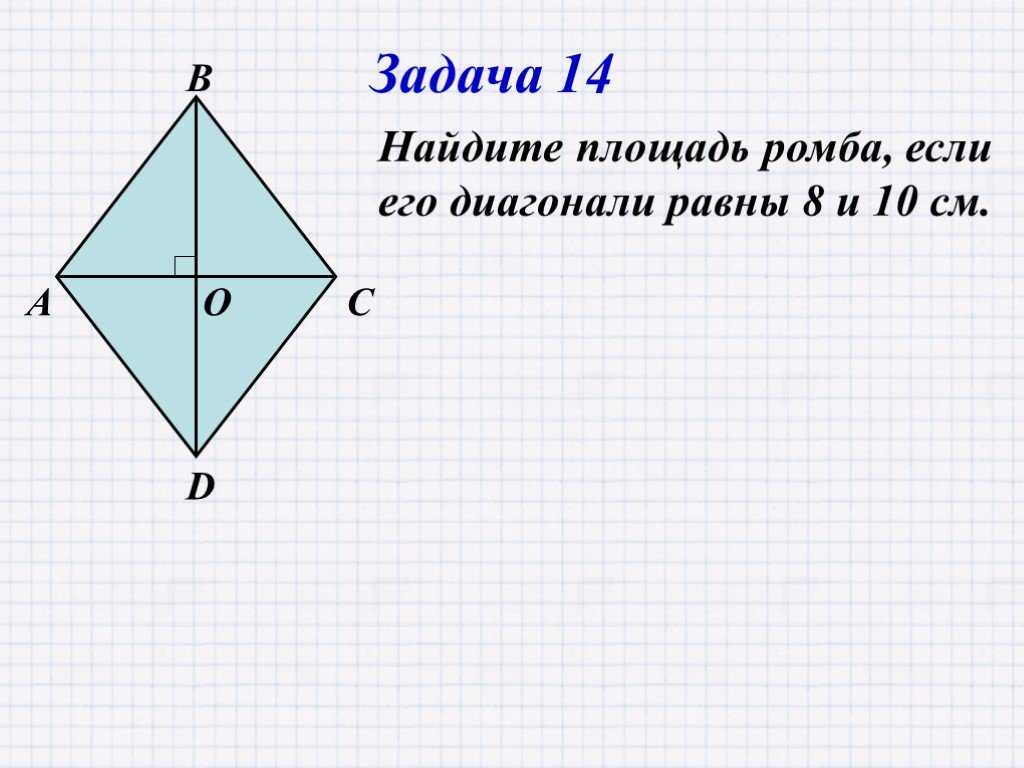

Задание 2Периметр ромба равен 44 см. Найдите сторону фигуры.

Решение:Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.

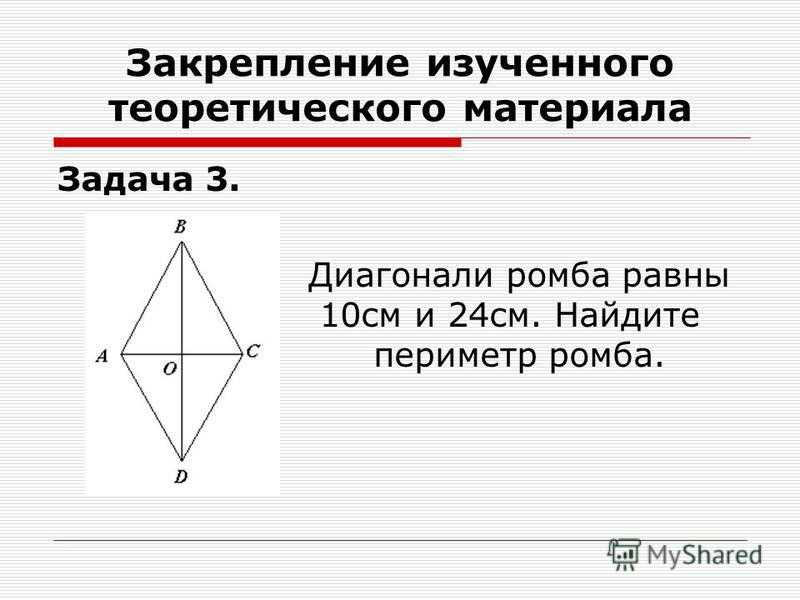
Задание 3Найдите периметр ромба, если известны его диагонали: 6 и 8 см.

Решение:Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Способы нахождения периметра

Через стороны

Поскольку у ромба все четыре стороны равны, его периметр можно выразить произведением длины одной стороны на 4.

P=4a

где P — периметр, a — длина стороны.

Нахождение периметра ромба можно проводить по еще одной формуле, используя длины диагоналей.

Через длину диагонали

Рассмотрим рисунок.

Проведем в ромбе ABCD диагонали BD и AC. Они пересекаются в точке O под прямым углом и делятся этой точкой пополам. Можно записать равенства:

AO=OC=d1/2

BO=OD=d2/2

В результате деления ромба диагоналями на четыре треугольника, имеющих прямые углы, образовались геометрические фигуры AOB, AOD, BOC, DOC. Подробнее рассмотрим один треугольник — AOB.

Из рисунка видно, что сторона AB являясь стороной ромба, представляет собой гипотенузу в прямоугольнике. Далее воспользуемся известной теоремой Пифагора:

AB2=AO2+OB2

В эту формулу подставим величины длин катетов. Однако перед этим выразим их через ½ диагоналей.

AB2=(d₁/2)2+(d₂/2)2

Извлекая квадрат из этого выражения, получаем:

AB=√((d₁/2)2+(d₂/2)2)

В итоге находим периметр ромба:

Нахождение периметра трапеции

Формула

Трапеция – это четырехугольник, отличающийся тем, что его две стороны параллельны, а другие две не параллельны.

Характеристики:

1. Основа трапеции – это те две параллельные стороны.
2. Боковые стороны – не параллельные стороны.
3. Если две боковые стороны равны, то можно сделать вывод, что такая трапеция равнобедренная.
4. Трапеция с прямыми углами является прямоугольной.
5. В трапеции можно провести среднюю линию, которая будет параллельна основаниям, а также равняться их полусумме.
6. Если трапеция равнобедренная, то ее углы и длины диагоналей равны.

Трапеция
Формула

Чтобы найти периметр трапеции, необходимо знать длины всех ее сторон, чтобы сложить их. Представим, что стороны трапеции – это a, b, c, d. Получается, для нахождения периметра трапеции, нам надо сложить все ее стороны:

\

Пример 1

Найдите периметр трапеции, если известно, что ее стороны равны: 2, 6, 5, 5.

Решение:

Используем формулу:

P = a + b + c + d

2 + 6 + 5 + 5 = 18 (см)

Ответ: периметр трапеции равен 18 см.