Как найти длину дуги окружности

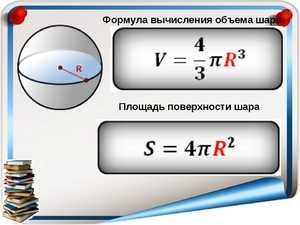
Применение формулы

Рассмотрим на примере, как вычислить площадь круглого шара
, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.

Формула вычисления площади
применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.

Формула вычисления объёма
может пригодиться и строительной бригаде, что делает ремонт

И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике

Но как быть, если не представляется возможным измерить объект?
Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.

Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара,
был Архимед
. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.

Именно Архимед определил границы числа «пи»
и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.

Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.

Формула объема шарового сектора как объем пирамиды

СÃÂõÃÂÃÂòÃÂõàõÃÂõ þôýð ÃÂþÃÂüÃÂûð, àÿþüþÃÂÃÂàúþÃÂþÃÂþù üþöýþ ýðùÃÂø øÃÂúþüÃÂù þñÃÂõü.

ÃÂýð ÃÂðòýð þñÃÂõüàÿøÃÂðüøôÃÂ, àúþÃÂþÃÂþù ÿûþÃÂðôàþÃÂýþòðýøàÃÂøÃÂûõýýþ ÃÂðòýð ÿûþÃÂðôø ÃÂðÃÂÃÂø ÃÂÃÂõÃÂøÃÂõÃÂúþù ÿþòõÃÂÃÂýþÃÂÃÂø, úþÃÂþÃÂðàòÃÂÃÂõ÷ðõÃÂÃÂàÃÂõúÃÂþÃÂþü. ÃÂÃÂÃÂþÃÂð ÿøÃÂðüøôàÃÂðòýð ÃÂðôøÃÂÃÂàÃÂðÃÂþòþóþ ÃÂõúÃÂþÃÂð.

àð÷ñõÃÂõü ÃÂõÃÂõýøõ ÷ðôðàýð ôðýýÃÂàÃÂõüÃÂ.

ÃÂõ ÷ýðõÃÂõ, óôõ ýðùÃÂø ÃÂõÃÂõýøõ ÷ðôðàýð ÷ðúð÷ ýõôþÃÂþóþ? ÃÂð ýðÃÂõü ÃÂðùÃÂõ õÃÂÃÂàÿÃÂþÃÂøûÃÂýÃÂõ øÃÂÿþûýøÃÂõûø, úþÃÂþÃÂÃÂõ ÿþüþóÃÂàòðü ò ÃÂÃÂþü!

Площадь сектора круга

Сектор круга

Каждый раз, когда вы отрезаете кусок от тыквенного пирога, круглого именинного торта или круглой пиццы, вы удаляете сектор.

сектор дуга

Дуги окружности

Острые центральные углы всегда будут давать малых дуг и малых секторов. Когда центральный угол, образованный двумя радиусами, равен 90°, сектор называется квадрантом (поскольку весь круг состоит из четырех квадрантов или четвертей). Когда два радиуса образуют 180° или половину окружности, сектор называется 9.0055 полукруг и имеет большую дугу .

В отличие от треугольников, границы секторов а не устанавливаются отрезками. Правда, у вас есть два радиуса, образующие центральный угол, но часть окружности, которая составляет третью «сторону», изогнута, поэтому найти площадь сектора немного сложнее, чем найти площадь треугольника.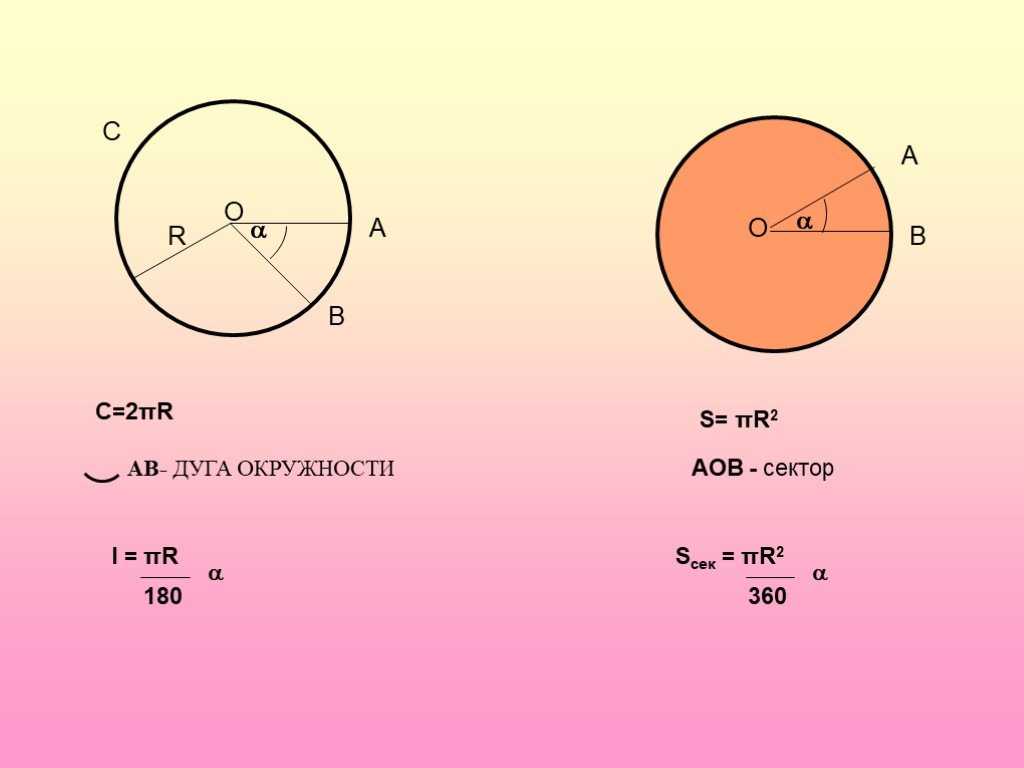

Как найти площадь сектора

Вы не можете найти площадь сектора, если не знаете радиус круга. Однако будьте осторожны; Вы можете найти радиус, если у вас есть диаметр или окружность. Возможно, вам придется сделать небольшую предварительную математику, чтобы получить радиус.

Найдите радиус окружности

При диаметре d окружности радиус r равен:

r=d2

При длине окружности C радиус r равен:

r=C(2π)

Зная радиус, вы получаете длины двух частей сектора. Вам нужно только знать длину дуги или центральный угол в градусах или радианах.

Площадь сектора Формула

Центральный угол позволяет узнать, какую часть или процент всего круга составляет ваш сектор. Квадрант имеет центральный угол 90° и составляет одну четвертую часть всего круга. Центральный угол 45° составляет одну восьмую часть окружности.

Это простые дроби, но что, если ваш центральный угол 9-дюймового тыквенного пирога равен, скажем, 31°?

[вставьте рисунок тыквенного пирога с сектором, разрезанным под углом +/- 31°]

Эта формула поможет вам найти площадь сектора A, если вы знаете центральный угол в градусах, n° и радиус, r, круга:

A = (n°360°) × π × r2

Для вашего тыквенного пирога подключите 31° и 9 дюймов:

A = (31360) × π × 92

A = 21,9126 in2

Площадь сектора в радианах

Если вместо центрального угла в градусах вам дано радиан , вы используете еще более простую формулу.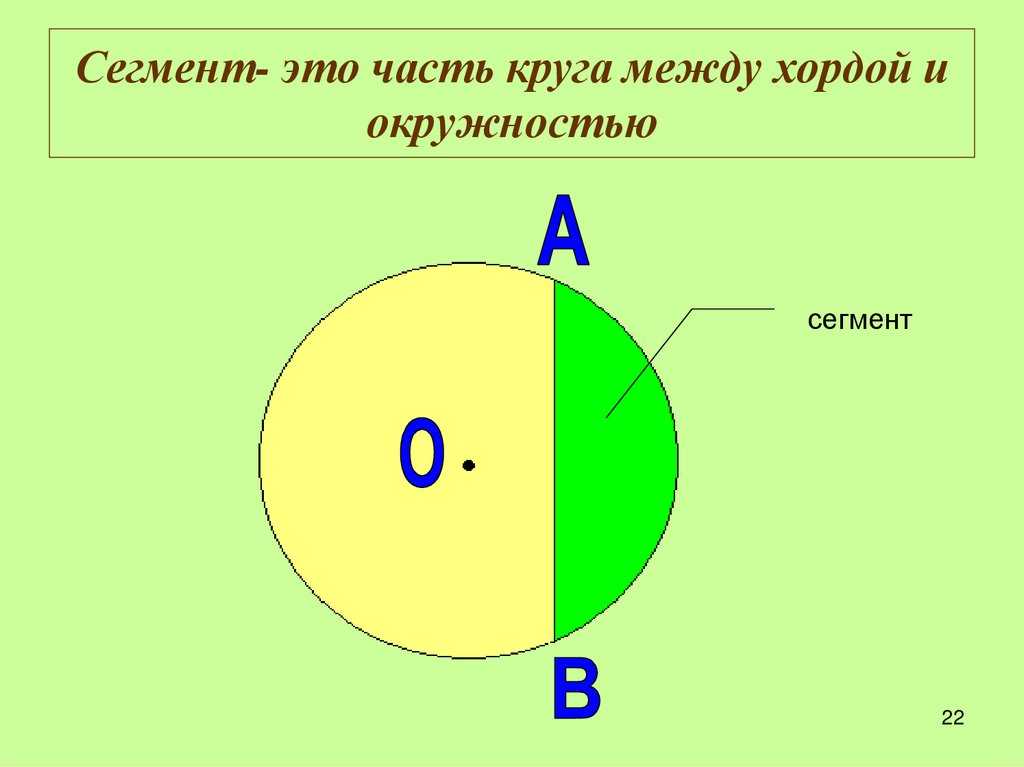

Чтобы найти площадь A сектора с центральным углом θ радиан и радиусом r:

A = (θ2) × r2

Наше любимое π, кажется, исчезло! На самом деле это не так. Радианы основаны на π (круг равен 2π радианам), поэтому на самом деле вы заменили n°360° на θ2π. Когда в нашей исходной формуле используется θ2π, она упрощается до элегантного (θ2) × r2.

Площадь сектора круга Примеры

У вас есть личная пицца диаметром 30 см. Вы разрезали его на шесть равных частей, так что центральный угол каждой части равен 60°. Какова площадь в квадратных сантиметрах каждого куска?

A = (n°360°) × π × r2

Сначала попробуйте сами, прежде чем смотреть вперед!

A = (60°360°) × π × 152

A = (16) × π × 225

A = 117,8097 см2

Вы не забыли взять половина диаметра найти радиус?

Пример площади сектора в радианах

Предположим, у вас есть сектор с центральным углом 0,8 радиана и радиусом 1,3 метра. Ваша формула:

A = (θ2) × r2

Попробуйте сами, прежде чем смотреть вперед!

A = (0,82) × 1,32

A = 0,676 м2

Занимательные факты

Это интересно:

1. У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
2. Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
3. Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.

Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.

Как найти площадь сферы

Запомните!

Формула площади сферы:

S = 4π
R 2

Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа .
Зная определение степени,
можно записать формулу площади сферы следующим образом. S = 4π
R 2 =
4π
R · R;

Закрепим полученные знания и решим задачу на площадь сферы.

Зубарева 6 класс. Номер 692(а)

Условие задачи:

• Вычислите площадь сферы, если её радиус равен
  
  1 =
  3 ·
  =
  =
  / (4 · 3)
  = ) =
  = ) =
  = =
  =

  88

  = 1

• R 3 = 1
• R = 1 м

Важно!

Уважаемые родители!

При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.

В 6 классе при решении такой задачи используйте метод перебора.

Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.

Имея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара. Формула будет иметь вид S =4πR2
, где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение.
Секущая сферы
— это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания
поверхности или точками входа и выхода на поверхности.

Определение.
Хорда сферы (шара)
— это отрезок, соединяющий две точки сферы (поверхности шара).

Определение.
Секущая плоскость
— это плоскость, которая пересекает сферу.

Определение.
Диаметральная плоскость
— это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность
и большой круг
. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d
от центра сферы до секущей всегда меньше чем радиус сферы:

d

Расстояние m
между секущей плоскостью и центром сферы всегда меньше радиуса R:

m

Местом сечения секущей плоскости на сфере всегда будет малая окружность
, а на шаре местом сечения будет малый круг
. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:

r
= √R 2 — m
2
,

Где R — радиус сферы (шара), m
— расстояние от центра шара до секущей плоскости.

Определение.
Полусфера (полушар)
— это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.
Касательная к сфере
— это прямая, которая касается сферы только в одной точке.

Определение.
Касательная плоскость к сфере
— это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение.
Сегмент шара
— это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента
называют круг, который образовался в месте сечения. Высотой сегмента
h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула.
Площадь внешней поверхности сегмента сферы
с высотой h
через радиус сферы R:

S = 2π
Rh

Мы даем здесь очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).

Тогда, обозначая через площадь этого участка — основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):

Если теперь всю поверхность шара разложить на очень большое число N таких малых областей , тем самым объем шара на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой

где последняя сумма равна полной поверхности шара:

Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу

Последний результат формулируется так:

Площадь поверхности шара равна учетверенной площади его большого круга.

Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. сферическую поверхность, или «шапочки»; см. рис. 409). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:

откуда находим для площади шапочки формулу

Шаровым поясом (см. рис. 408) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек:

где — высота слоя. Итак, площадь поверхности шарового пояса для данного шара зависит только от высоты соответствующего слоя, но не от его положения на шаре.

Задача. Боковая поверхность конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара. Найти высоту конуса, если радиус шара равен .

Решение. Введем для удобства угол а между высотой и образующей конуса (рис. 413). Найдем для высоты, радиуса основания и образующей конуса выражения

Определение шара

Шаром
называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее R R
R

— радиус этого шара.

Как найти площадь сектора круга: формулы, примеры задач

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади сектора круга

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.

• Определение сектора круга
• Формулы нахождения площади сектора круга
  • Через длину дуги и радиус круга
  • Через угол сектора (в градусах) и радиус круга
  • Через угол сектора (в радианах) и радиус круга
• Примеры задач

Определение сектора круга

Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.

• AB – дуга сектора;
• R (или r) – радиус круга;
• α – это угол сектора, т. е. угол между двумя радиусами. Также его иногда называют центральным углом.

Формулы нахождения площади сектора круга

Через угол сектора (в радианах) и радиус круга

Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (a_рад) и квадрата радиуса круга.

Примеры задач

Задание 1Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.

РешениеВоспользуемся первой формулой, подставив в нее заданные значения:

Задание 2Найдите угол сектора, если известно, что его площадь равна 78 см2, а радиус круга – 8 см.

РешениеВыведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Формула площади поверхности шара по радиусу шара

S = 4 ⋅ π ⋅ R 2 S=4\cdot\pi\cdot R^2
S
=

4
⋅

π
⋅

R
2

R R
R

— радиус шара.

Шар вписан в куб, диагональ которого d d
d

равна 300 \sqrt{300}
3
0
0

​

(см.). Найти площадь поверхности шара.

Решение

D = 300 d= \sqrt{300}
d
=

3
0
0

​

Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через a a
a

. Тогда, по теореме Пифагора:

D 2 = a 2 + a 2 + a 2 d^2=a^2+a^2+a^2
d
2

=

a
2

+

a
2

+

a
2

D 2 = 3 ⋅ a 2 d^2=3\cdot a^2
d
2

=

3
⋅

a
2

A = d 3 a=\frac{d}{\sqrt{3}}
a
=

3

​

d

​

A = 300 3 = 100 = 10 a=\frac{\sqrt{300}}{\sqrt{3}}=\sqrt{100}=10
a
=

3

​

3
0
0

​

​

=

1
0
0

​

=

1
0

Радиус шара, вписаного в куб равен половине стороны этого куба:

R = a 2 = 10 2 = 5 R=\frac{a}{2}=\frac{10}{2}=5
R
=

2

a

​

=

2

1
0

​

=

5

Тогда площадь поверхности шара:

S = 4 ⋅ π ⋅ R 2 = 4 ⋅ π ⋅ 5 2 ≈ 314 S=4\cdot\pi\cdot R^2=4\cdot\pi\cdot 5^2\approx314
S
=

4
⋅

π
⋅

R
2

=

4
⋅

π
⋅

5
2

≈

3
1
4

(см. кв.)

Ответ:
314 см. кв.

Объем шара

Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.

Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3

Объем цилиндра вычисляется по формуле:

Vc = pi × R 2 × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R 3 .

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3

Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же

Vsh = 4/3 pi × R 3

Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.

Как найти площадь поверхности сегмента шара: формула, пример

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади шарового сегмента

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.

• Определение сегмента шара
• Формулы для нахождения площади сегмента шара
  • Площадь основания
  • Площадь сферической поверхности
  • Площадь полной поверхности
• Пример задачи

Определение сегмента шара

Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью.

• R – радиус шара;
• r – радиус основания сегмента;
• h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Формулы для нахождения площади сегмента шара

Площадь основания

Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):

S_осн. = πr 2

Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.

Площадь сферической поверхности

Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.

S_{сфер. пов.} = 2πRh

Площадь полной поверхности

Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.

S_полн. = S_осн. + S_{сфер. пов.} = π (2Rh + r 2)

Пример задачи

Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.

Решение

Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.

S_осн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2

S_{сфер. пов.} = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2

S_полн. = S_осн. + S _{сфер. пов.} = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы