Мбоу «славкинская средняя школа»

Содержание

1. Определения
2. Пример решения задачи
3. Что мы узнали?

Бонус

Тест по теме

• Площадь прямоугольного треугольника
• Высота треугольника
• Площадь правильного треугольника
• Площадь прямого треугольника
• Площадь равностороннего треугольника
• Площадь равнобедренного треугольника
• Медиана треугольника
• Правильный треугольник Тупоугольный треугольник
• Остроугольный треугольник
• Свойства прямоугольного треугольника
• Стороны прямоугольного треугольника
• Средняя линия прямоугольного треугольника
• Признаки подобия прямоугольных треугольников
• Высота равностороннего треугольника
• Медиана равностороннего треугольника
• Неравенство треугольника
• Длина медианы правильного треугольника
• Равнобедренный тупоугольный треугольник
• Средняя линия прямоугольного треугольника
• Длина средней линии треугольника

показать все

По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.

1. 1. Михаил Тяпин 214
2. 2. Наталия Дробот 198
3. 3. Мария Кауфман 192
4. 4. Игорь Проскуренко 157
5. 5. Соня Зверева 153
6. 6. Василиса Варавкина 119
7. 7. Иоанн Стефановский 107
8. 8. Софья Холена 94
9. 9. Оля Проскурина 85
10. 10. Татьяна Бежина 83

1. 1. Мария Николаевна 13,500
2. 2. Лариса Самодурова 12,695
3. 3. Liza 12,310
4. 4. Кристина Волосочева 11,445
5. 5. TorkMen 11,441
6. 6. Ekaterina 11,176
7. 7. Влад Лубенков 11,100
8. 8. Лиса 11,070
9. 9. Юлия Бронникова 11,060
10. 10. Вячеслав 10,840

Самые активные участники недели:

• 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
• 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
• 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.

Три счастливчика, которые прошли хотя бы 1 тест:

• 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
• 2. Николай З — подарочная карта книжного магазина на 500 рублей.
• 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.

Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим виды треугольников и научимся строить прямоугольный треугольник на нелинованной бумаге. Вначале вспомним определение треугольника и его элементы, какие существуют виды углов, узнаем, как на нелинованной бумаге построить прямой угол. Далее узнаем, как делятся треугольники на виды в зависимости от типа углов в них. Рассмотрим несколько задач на нахождение вида треугольников и на построение

Построение угла, равного данному

Задача

Отложить от данного луча угол, равный данному.

Решение

Данный угол с вершиной А и луч ОМ изображены на рисунке 84. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ.

Рис. 84

Проведём окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. 85, а). Затем проведём окружность того же радиуса с центром в начете данного луча ОМ. Она пересекает луч в точке D (рис. 85, б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ — искомый.

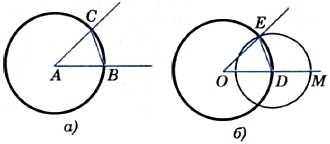
Рис. 85

Рассмотрим треугольники АВС и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. 85, б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE.

Следовательно, ΔАВС = ΔODE по трём сторонам. Поэтому ∠DOE = ∠BAC, т. е. построенный угол МОЕ равен данному углу А.

То же построение можно выполнить и на местности, если вместо циркуля воспользоваться верёвкой.

Простые углы

Простой угол – это угол, который меньше 90 градусов, или как его еще называют – острый угол. Например, угол между лучами АВ и АС (А – вершина угла) является простым, если он меньше 90 градусов.

Простые углы часто встречаются в повседневной жизни. Например, когда мы готовим пищу, мы используем заточенный нож для того, чтобы нарезать фрукты или овощи под углом, который является простым. Также простые углы встречаются в архитектуре и строительстве.

Острый простой угол можно изобразить красиво на бумаге или компьютере. Для этого можно использовать программы для рисования, такие как Paint или Adobe Photoshop. Простым углом можно поработать и при решении математических задач. Например, ученик может использовать простые углы при решении задач на геометрические фигуры.

Все простые углы имеют одинаковое определение и свойства, которые можно использовать при решении задач. Знание о простых углах поможет ученику лучше понимать геометрию и успешно решать задачи на экзамене или контрольной работе.

Углы в треугольнике

Треугольник — это геометрическая фигура, состоящая из трёх линейных отрезков, соединяющих три точки, которые не лежат на одной прямой. В треугольнике есть три внутренних угла, которые образуются между его сторонами. Сумма внутренних углов в треугольнике всегда равна 180 градусам.

Если все углы треугольника меньше 90 градусов, то такой треугольник называется остроугольным. Если же хотя бы один угол больше 90 градусов, то такой треугольник называется тупоугольным.

Кроме того, в треугольнике может быть выделена особая линия, которая соединяет вершину треугольника с серединой противоположной стороны. Такая линия называется медианой треугольника и пересекает каждую из сторон треугольника в точке, равноудалённой от её концов.

Изучая углы в треугольнике, можно понять много интересных и полезных свойств этой фигуры, которые могут пригодиться при решении геометрических задач.

Соотношение отрезков и углов

Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.

Большие и меньшие длины

Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.

Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.

Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.

Рассмотренные теоремы приводят к двум важным следствиям:

1. Против равных сторон лежат равные углы, и наоборот. Следствие актуально для равносторонних и равнобедренных фигур.
2. Гипотенуза в треугольнике с прямым углом является самой длинной стороной, поскольку она лежит напротив самого большого угла.

Теоремы косинусов и синусов

Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:

c 2 = a 2 + b 2 — 2*a*b*cos.

Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.

Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:. a/sin (A) = b/sin (B) = c/sin.

a/sin (A) = b/sin (B) = c/sin.

Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).

Прямоугольный треугольник

Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:

c 2 = a 2 + b 2 .

Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:

sin (45 °) = a/c = ½ 0,5.

Это соотношение можно получить также из теоремы Пифагора.

Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:

sin (30 °) = ½ = a/c.

Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.

Свойства перпендикулярных прямых

Сначала разберём два «стандартных» свойства, которые вы найдёте в любом учебнике геометрии 7-го класса. А затем — одно «нестандартное», но именно оно чаще всего и встречается в настоящих задачах.

3.1. Теорема о двух прямых, перпендикулярных третьей

Прямая $AB\bot EF$ и прямая $MN\bot EF$. Следовательно, прямые $AB$ и $MN$ не пересекаются. Проще говоря, они параллельны (см. урок «Параллельные прямые»).

3.2. Теорема о прямой, перпендикулярной данной

Доказательство этой теоремы состоит из двух частей: сначала докажем, что такую прямую провести можно, а затем — что она единственная.

Прямая, перпендикулярная данной, строится очень просто. Рассмотрим прямую $a$, на которой отмечена точка $M$:

Отложим от луча $MK$ угол, равный 90°. В любую сторону: в верхнюю полуплоскость или нижнюю — не имеет значения. Получим луч $MN$:

Наконец, продолжим луч $MN$ в противоположную другую сторону (т.е. построим дополнительный луч). Получим искомую прямую $MN\bot a$:

Единственность такого построения следует либо из аксиомы о том, что нужный угол можно отложить в нужном направлении одним и только одним способом, либо из предыдущей теоремы о двух прямых, перпендикулярных данной. В самом деле, пусть есть ещё одна прямая $ML$, которая, как и $MN$, перпендикулярна прямой $a$:

Поскольку $MN\bot a$ и $ML\bot a$, по предыдущей теореме эти прямые не пересекаются. Что противоречит нашему построению, в котором у прямых $MN$ и $ML$ есть общая точка $M$. Следовательно, прямые $MN$ и $ML$ совпадают, что и требовалось доказать.

3.3

Важное свойство прямого угла. Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах

Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Это утверждение может показаться очевидным. И оно действительно является таковым. Однако деление прямого угла на части встречается в задачах настолько часто, что я не мог не упомянуть об этом.

Кроме того, начинающие ученики часто не замечают такие углы на чертежах. Поэтому сейчас мы будем отрабатывать эту теорему на реальных задачах.

Центральный и вписанный угол

Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.

• Центральный угол — угол с вершиной в центре окружности. Величина центрального угла равна градусной мере дуги, заключённой между сторонами этого угла.
• Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Величина вписанного угла равна половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол θ равен половине величины центрального угла 2θ, , опирающегося у основания на окружности на ту же самую дугу (розового цвета). То есть угол θ не меняет своей величины от вершины к вершине, взятой на окружности (зелёный и голубой углы). Внешний угол для вписанного с другой стороны угла окружности имеет ту же величину θ (коричневого цвета)

Величина вписанного угла равна половине величины центрального угла, опирающегося у основания на окружности на ту же самую дугу (см. рис.).

Виды углов: острый, прямой, тупой, полный

Острый угол

Острый угол это угол, значение которого меньше 90 градусов. В произвольном параллелограмме всегда есть два острых и два тупых угла, тогда как в произвольном треугольнике все углы прямые. Если хоть один из углов треугольника прямой или тупой, то фигуру уже нельзя считать произвольной.

Рис. 1. Острый угол.

Прямой угол

Прямой угол очень много значит в геометрии. Прямой угол в параллелограмме, означает, что перед вами квадрат или прямоугольник. Произвольный треугольник, если доказать, что в нем есть прямой угол, сразу же превращается в прямоугольный треугольник, для которого действует больший набор теорем и правил, нежели для произвольного.

Рис. 2. Прямой угол.

Тупой угол

Тупой угол, это угол больше 90 градусов. Это значение очень широко используется в задачах по тригонометрии. Но и в геометрии очень часто можно встретить задачи на тупоугольный треугольник. Считается, что тупоугольный треугольник сложнее воспринимается чисто визуально, но на деле, стоит только привыкнуть и задачи эти уже не будут казаться такими страшными.

Рис. 3. Тупой угол.

Полный угол

Полный угол это угол в 360 градусов. То есть тот самый момент, когда минутная и часовая стрелка совпадает.

Тогда с одной стороны будет полный угол, а с другой угол в 0 градусов. Чисто теоретически и нулевой угол тоже существует, он означает, что стрелки или лучи друг от друга не отклонялись.

Что мы узнали?

Мы узнали, что такое угол, определили виды углов, поговорили о том, какую роль каждый из видов играет в геометрии и привели примеры каждого из них.

1. /10

   Вопрос 1 из 10

Задачи

Задача 1

Имеется геометрическая фигура в виде пирамиды с четырьмя углами и равными между собой ребрами. При этом в основании фигуры расположен квадрат. Требуется определить, чему равен \(6\cos \alpha\) , если за \(\alpha\) обозначен угол, разделяющий смежные боковые грани.

Решение

Предположим, что искомая пирамида имеет следующее название SABCD. Пусть S играет роль вершины геометрической фигуры, а ее ребра соответствуют а. Тогда, согласно условию задания, требуется найти угол, разделяющий грани SAD и SCD.

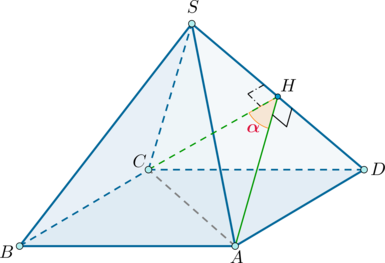
Построим \(CH\perp SD\). Заметим, что:

\(\triangle SAD=\triangle SCD\)

В этом случае AH также играет роль высоты в \(\triangle SAD\). Таким образом, исходя из определения:

\(\angle AHC=\alpha\)

Заметим, что \(\alpha\) является линейным углом, разделяющим грани SAD и SCD. При условии квадратного основания в пирамиде запишем следующее:

\(AC=a\sqrt2\)

Кроме того, имеет место такое равенство:

CH=AH

Высота AH находится в треугольнике с одинаковыми сторонами, равными а. Таким образом:

\(CH=AH=\frac{\sqrt3}2a\)

Воспользуемся теоремой косинусов применительно к \(\triangle AHC\):

\(\cos \alpha=\dfrac{CH^2+AH^2-AC^2}{2CH\cdot AH} =-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\)

Ответ: -2.

Задача 2

На рисунке изображено пересечение плоскостей, обозначенных за \(\pi_1\) и \(\pi_2\). В результате образуется общая прямая l с точками M и N. Полученные отрезки MA и MB расположены перпендикулярно по отношению к прямой l, а также принадлежат плоскостям за \(\pi_1\) и \( \pi_2\) соответственно. При этом справедливы следующие равенства: MN = 15; AN = 39; BN = 17; AB = 40. Необходимо вычислить \(3\cos\alpha\) , где \(\alpha\) является углом, разделяющим плоскости  \(\pi_1\) и \(\pi_2\) .

Решение

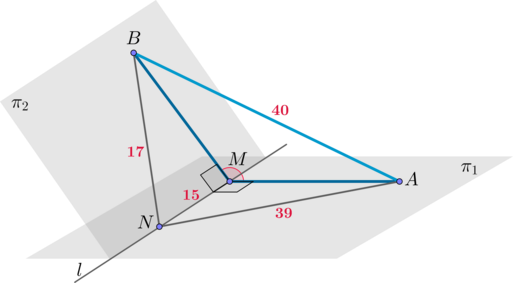
Заметим, что треугольник AMN обладает прямым углом, тогда:

\(AN^2 = AM^2 + MN^2\)

В результате:

\(AM^2 = 39^2 — 15^2 = 36^2\)

Прямоугольным также является треугольник BMN. В таком случае:

\(BN^2 = BM^2 + MN^2\)

Исходя из этого, получим:

\(BM^2 = 17^2 — 15^2 = 8^2\)

Воспользуемся теоремой косинусов применительно к треугольнику AMB:

\(AB^2 = AM^2 + MB^2 — 2\cdot AM\cdot MB\cdot\cos\angle AMB\)

Таким образом:

\(40^2 = 36^2 + 8^2 — 2\cdot 36\cdot 8\cdot\cos\angle AMB\qquad\Leftrightarrow\qquad \cos\angle AMB = -\dfrac{5}{12}\)

Исходя из того, что угол \(\alpha\), разделяющий плоскости, является острым, а угол \(\angle AMB\) определяется как тупой, получим следующее равенство:

\(\cos\alpha=\dfrac5{12}\)

\(3\cos\alpha = \dfrac54=1,25\)

Ответ: 1,25.

Задача 3

На рисунке изображен квадрат ABCD. В точке О пересекаются диагонали. Точка S расположена за пределами квадратной плоскости, а \(SO \perp ABC\). Требуется вычислить угол, разделяющий плоскости ASD и ABC, при условии, что SO = 5, а AB = 10.

Решение

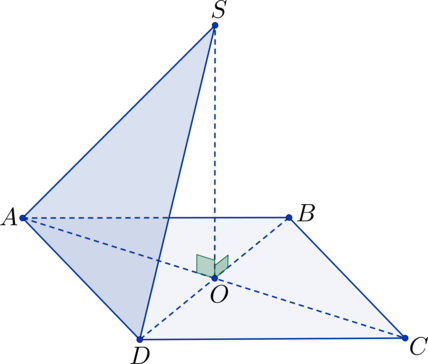
Геометрические фигуры в виде треугольников с прямыми углами \(\triangle SAO\) и \(\triangle SDO\) являются идентичными, согласно паре сторон и углу, который их разделяет:

\(SO \perp ABC \Rightarrow \angle SOA = \angle SOD = 90^\circ\)

AO = DO

Записанные выше равенства являются справедливыми, так как в точке O пересекаются диагонали квадрата, а SO служит общей стороной.

\(\Rightarrow AS = SD \Rightarrow \triangle ASD\)

\(\triangle ASD\) является равнобедренным. Точка K делит пополам AD. В таком случае SK представляет собой высоту в треугольнике \(\triangle ASD\), а OK обозначает высоту в треугольнике AOD. Таким образом, плоскость SOK расположена под прямым углом к плоскостям ASD и ABC. Можно сделать вывод о том, что \(\angle SKO\)  является линейным углом, который соответствует искомому двугранному углу.

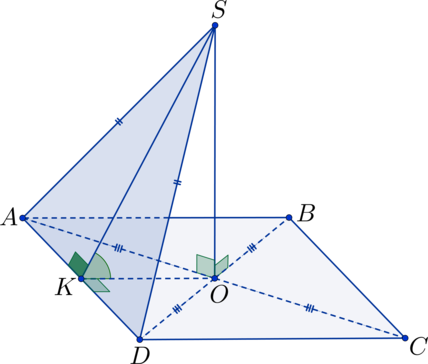
Рассмотрим треугольник \(\triangle SKO\):

\(OK = \frac{1}{2}\cdot AB = \frac{1}{2}\cdot 10 = 5 = SO\)

Таким образом, \(\triangle SOK\) является равнобедренным прямоугольным треугольником. Тогда:

\(\angle SKO = 45^\circ.\)

Сравнение углов

Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:

\ и \ полностью совмещаются при наложении следовательно: \

\ и \ не совмещаются при наложении: \

Причем: \

При этом развернутые углы всегда являются равными.

Совмещение углов \ и \ происходит следующим образом:

1. Вершину B одного угла совмещаем с вершиной N другого угла.
2. Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.

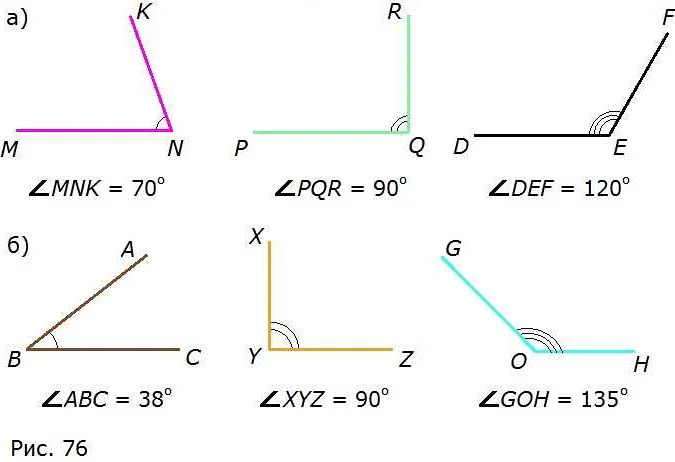
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.

Если нет, то один угол — меньше другого: ∠ABC<∠MNK.

Некоторые важные теоремы, основанные на прямых и углах:

1. Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
2. Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
3. Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
4. Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
5. Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.

Определение угла в математике

Определение

Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.

Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.

Стороны угла – лучи, которые образуют угол (А, В).

Вершина угла – точка, из которой выходят лучи (О).

Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.

Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.

• Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
• Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.

Интересно

Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».

Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.

Как обозначить углы?

Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:

• Способ 1: Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.
• Способ 2:Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.

Типы углов

Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.

1. Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
2. Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
   Прямой угол можно легко наблюдать, так как он образует форму буквы L.
3. Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
   это тупой угол.
4. Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
   половина полного оборота круга. Размер прямого угла равен 180°.
5. Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
6. Полный угол — когда измерение угла равно 360 градусам, это полный угол.

Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.

Некоторые интересные факты об углах

1. Углы — это важная часть геометрии

Углы — это очень важная часть геометрии. Они используются для определения, измерения и описания форм объектов.

2. Угол — это две линии, встречающиеся в одной точке

Чтобы сформировать угол, нужно две линии, которые затем встречаются в одной точке, называемой вершиной.

3. Самый маленький угол, который можно измерить, равен 1 градусу

Угол может быть измерен в различных единицах измерения, но самый маленький угол, который можно измерить, равен 1 градусу.

4. Углы могут быть меньше или больше 90 градусов

Угол, который меньше 90 градусов, называется острым углом. Угол, который больше 90 градусов, называется тупым углом.

5. Сумма углов в треугольнике равна 180 градусам

Сумма углов в треугольнике всегда равна 180 градусам. Это объясняется тем, что треугольник содержит три угла.

Угол и скалярное произведение

Понятие угла можно определить для линейных пространств произвольной природы (и произвольной, в том числе бесконечной размерности), на которых аксиоматически введено положительно определённое скалярное произведение (x,y){\displaystyle (x,y)} между двумя элементами пространства x{\displaystyle x} и y.{\displaystyle y.} Скалярное произведение позволяет определить также и так называемую норму (длину) элемента как квадратный корень произведения элемента на себя ||x||=(x,x).{\displaystyle ||x||={\sqrt {(x,x)}}.} Из аксиом скалярного произведения следует неравенство Коши — Буняковского (Коши — Шварца) для скалярного произведения: |(x,y)|⩽||x||⋅||y||,{\displaystyle |(x,y)|\leqslant ||x||\cdot ||y||,} откуда следует, что величина (x,y)||x||⋅||y||{\displaystyle {\frac {(x,y)}{||x||\cdot ||y||}}} принимает значения от −1 до 1, причём крайние значения достигаются тогда и только тогда, когда элементы пропорциональны (коллинеарны) друг другу (говоря геометрически — их направления совпадают или противоположны). Это позволяет интерпретировать отношение (x,y)||x||⋅||y||{\displaystyle {\frac {(x,y)}{||x||\cdot ||y||}}} как косинус угла между элементами x{\displaystyle x} и y.{\displaystyle y.} В частности, элементы называют ортогональными, если скалярное произведение (или косинус угла) равно нулю.

В частности, можно ввести понятие угла между непрерывными на некотором интервале a,b{\displaystyle } функциями, если ввести стандартное скалярное произведение (f,g)=∫abf(x)g(x)dx,{\displaystyle (f,g)=\int _{a}^{b}f(x)g(x)dx,} тогда нормы функций определяются как ||f||2=∫abf2(x)dx.{\displaystyle ||f||^{2}=\int _{a}^{b}f^{2}(x)dx.} Тогда косинус угла определяется стандартным образом как отношение скалярного произведения функций к их нормам. Функции также можно назвать ортогональными, если их скалярное произведение (интеграл их произведения) равно нулю.

В римановой геометрии можно аналогично определить угол между касательными векторами с помощью метрического тензора gij.{\displaystyle g_{ij}.} Скалярное произведение касательных векторов u{\displaystyle u} и v{\displaystyle v} в тензорной записи будет иметь вид: (u,v)=gijuivj,{\displaystyle (u,v)=g_{ij}u^{i}v^{j},} соответственно нормы векторов — ||u||=|gijuiuj|{\displaystyle ||u||={\sqrt {|g_{ij}u^{i}u^{j}|}}} и ||v||=|gijvivj|.{\displaystyle ||v||={\sqrt {|g_{ij}v^{i}v^{j}|}}.} Поэтому косинус угла будет определяться по стандартной формуле отношения указанного скалярного произведения к нормам векторов: cos⁡θ=(u,v)||u||⋅||v||=gijuivj|gijuiuj|⋅|gijvivj|.{\displaystyle \cos \theta ={\frac {(u,v)}{||u||\cdot ||v||}}={\frac {g_{ij}u^{i}v^{j}}{\sqrt {|g_{ij}u^{i}u^{j}|\cdot |g_{ij}v^{i}v^{j}|}}}.}

Неравенство треугольника

Следующий факт касается не углов, а сторон треугольника.

Это означает, что:

• \( a+b>c\)
• \( a+c>b\)
• \( b+c>a\)

Ты уже догадался, почему этот факт называется неравенством треугольника?

Ну вот, а где же это неравенство треугольника может оказаться полезным?

А представь, что у тебя есть три друга: Коля, Петя и Сергей.

И вот, Коля говорит: «От моего дома до Петиного \( 100\) м по прямой». А Петя: «От моего дома до дома Сергея \( 200\) метров по прямой». А Сергей: «Вам хорошо, а от моего дома до Колиного аж \( 500\) м по прямой».

Ну, тут уже ты должен сказать: «Стоп, стоп! Кто – то из вас говорит неправду!»

Так не может быть!

Почему?

Да потому что если от Коли до Пети \( 100\) м, а от Пети до Сергея \( 200\) м, то от Коли до Сергея точно должно быть меньше \( 300\) (\( =100+200\)) метров – иначе и нарушается то самое неравенство треугольника.

Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой (\( КС\)) должен быть короче, чем путь с заходом в точку \( П\). (\( К-П-С\)).

Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:

Бывает ли треугольник со сторонами \( 1,3,7\)?

Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: \( 1+3<7\), значит, треугольника со сторонами \( 1,3\) и \( 7\) не бывает! А вот со сторонами \( 2,4,5\) – бывает, потому что

Определение

Что такое угол? Существует три определения угла. Рассмотрим каждое из них, выберем наиболее простое и понятное.

Угол – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. То есть это просто два луча. Это определение дается практически в каждом учебнике геометрии. Оно правильное, но прочитав его, не совсем понятно, откуда берется значение угла.

Угол – это плоскость, ограниченная двумя лучами, исходящими из одной точки. То есть, два луча “откусывают кусочек пространства”.

Угол – это мера поворота луча, вокруг своего начала. Это сложно понять, но легко представить. Представьте часы. Вот на часах 12 часов дня, минутная и часовая стрелка находятся на одном уровне, тут минутная стрелка начинает двигаться. И каждый раз, время, а значит положение стрелок можно определить именно углом между часовой и минутной стрелкой. Углы могут быть разными, но если выделять угол в каждый момент времени дугой, то можно заметить, что дуга в конце концов превратится в круг.

Именно круг и является началом отчета для градуса. Дуга $$1\over360$$ части круга это градус. А по количеству градусов в угле можно выделить основные виды углов между прямыми: острые, прямые, тупые и полные углы.