Пример задач
Пример 1
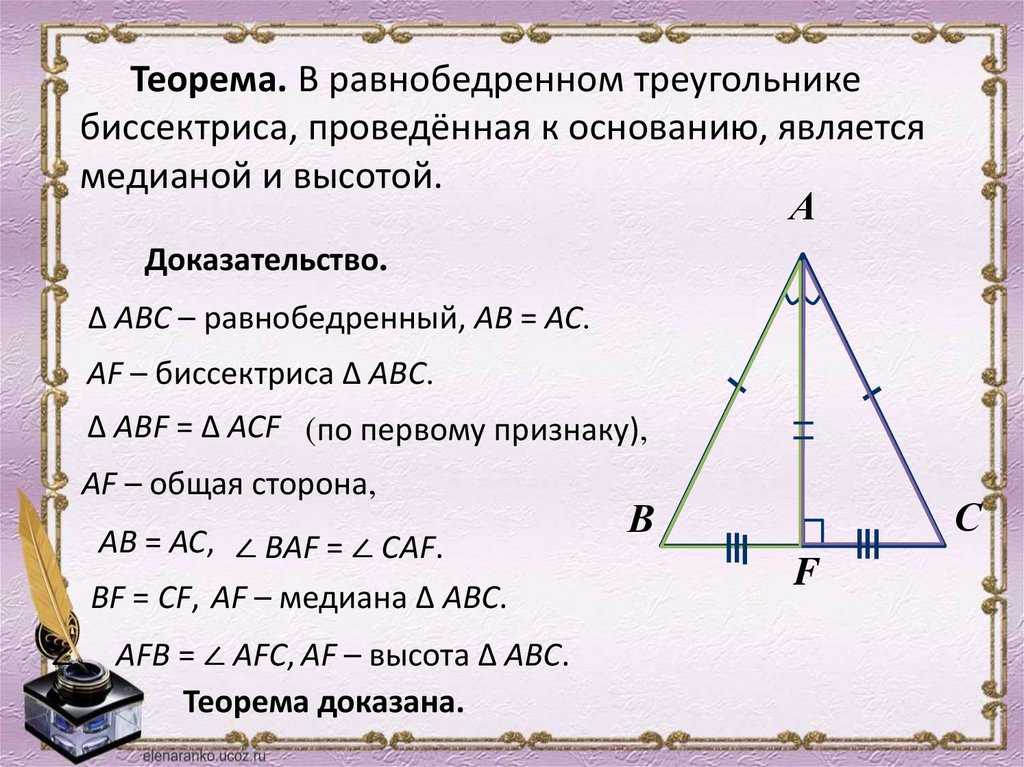
Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то треугольник является равнобедренным.
Доказательство.
Для этого нам нужно доказать, что $AB=BC$.
Изобразим рисунок по условию задачи (рис. 4).

Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$
Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$
У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.
Пример 2
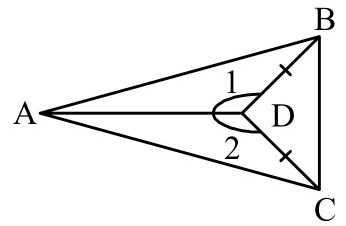
Пусть дан треугольник $ABC$. Доказать, что он будет равнобедренным в условиях рисунка 5.
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона $BD$ равняется стороне $CD$. Так как у треугольников $ADB$ и $ADC$ сторона $AD$ является общей, то треугольники $ADB$ и $ADC$ будут равняться по первому признаку. Но тогда и стороны $AB$ и $AC$ также равны между собой. Следовательно, данный треугольник будет равнобедренным.
Равнобедренный треугольник. Средний уровень
| Треугольник называется равнобедренным, если у него есть две равные стороны. |
- Эти две равные стороны называются боковыми сторонами, а третья сторона – основание равнобедренного треугольника.
- Посмотри на рисунок: и – боковые стороны, – основание равнобедренного треугольника.
Свойства равнобедренного треугольника:
|
Давай на одном рисунке поймём, почему так выходит. Проведем из точки высоту .
| Что получилось? Треугольник разделился на два прямоугольных треугольника и . И эти треугольники равны! У них равны гипотенузы и общий катет . |
Значит, у них равны все соответствующие элементы.
То есть:
|
Всё! Одним махом (высотой ) доказали сразу все утверждения.
И ты запомни: чтобы решить задачу про равнобедренный треугольник часто бывает очень полезно опустить высоту на основание равнобедренного треугольника и разделить его на два равных прямоугольных треугольника.
Признаки равнобедренного треугольника
Верны и обратные утверждения:
|
Почти все из этих утверждений снова можно доказать «одним махом».
1. Итак, пусть в оказались равны и .
Проведём высоту . Тогда
| – как прямоугольные по катету и острому углу. |
Значит, .
| Доказали, что – равнобедренный. |
2. a) Теперь пусть в каком–то треугольнике совпадают высота и биссектриса.
| Тогда снова по катету и острому углу. Значит, опять . |
2. б) А если совпадают высота и медиана? Все почти так же, ничуть не сложнее!
| — по двум катетам |
2. в) А вот если нет высоты, которая опущена на основание равнобедренного треугольника, то нет и никаких изначально прямоугольных треугольников. Плохо!
- Но выход есть – читай его в следующем уровне теории, поскольку тут доказательство посложнее, а пока просто запомни, что если медиана и биссектриса совпали, то треугольник тоже окажется равнобедренным, и высота всё-таки тоже совпадёт с этими биссектрисой и медианой.
- Подытожим:
- Если треугольник равнобедренный, то углы при основании равны, и высота, биссектриса и медиана, проведенные к основанию, совпадают.
- Если в каком-то треугольнике найдутся два равных угла, или какие-то две из трех линий (биссектриса, медиана, высота) совпадут, то такой треугольник – равнобедренный.
Равнобедренный треугольник. Краткое описание и основные формулы
Равнобедренный треугольник — треугольник, у которого есть две равные стороны.
|
Свойства равнобедренного треугольника:
|
Признаки равнобедренного треугольника:
- Если в некотором треугольнике два угла равны, то он – равнобедренный.
- Если в некотором треугольнике совпадают: а) высота и биссектриса или б) высота и медиана или в) медиана и биссектриса, проведённые к одной стороне, то такой треугольник – равнобедренный.
Свойства и признаки равнобедренного треугольника
| О нас |
| Демоверсии |
| Учебные пособия |
| Справочник по математике |
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство | Углы при основании равнобедренного треугольника | Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак | Высота треугольника, совпадающая с медианой | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак | Высота треугольника, совпадающая с биссектрисой | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак | Биссектриса треугольника, совпадающая с медианой | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
| Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство: углы при основании равнобедренного треугольника | |
| Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак: два равных угла треугольника | |
| Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
| В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак: высота треугольника, совпадающая с медианой | |
| Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак: высота треугольника, совпадающая с биссектрисой | |
| Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак: биссектриса треугольника, совпадающая с медианой | |
| Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение равнобедренного треугольника |
|
| Свойство углов при основании равнобедренного треугольника |
| Свойство:Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
| Признак:Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
| Свойство:В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
| Признак:Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
| Признак:Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
| Признак:Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Высота равнобедренного треугольника
Итак, провели высоту. Что же получилось?
Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.
Смотри:
Тоже два прямоугольных….
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
Видишь, два прямоугольных треугольника (Δ???????????? и Δ????????????) – одинаковые!
Или, как математики любят говорить? Равные!
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём?
Онлайн калькулятор
Чтобы вычислить Высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину двух равных сторон (a) и длину основания (b) длину двух равных сторон (a) и угол α длину двух равных сторон (a) и угол β длину основания (b) и угол α длину основания (b) и угол β
Введите их в соответствующие поля и получите результат.
Если известны длина стороны а и основания b
Чему равна высота h равнобедренного треугольника если Длина сторон , а Длина основания
Чему равна высота H у равнобедренного треугольника если известны длина стороны A и длина основания B?
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
H = √ 10 2 — ( 5 /2) 2 = √ 100 — 6.25 ≈ 9.68 см
Если известны длина стороны а и угол α
Чему равна высота h равнобедренного треугольника если длина сторон, а угол
Чему равна высота H у равнобедренного треугольника если известны длина стороны A и угол Α?
Пример
Если сторона a = 5 см, а ∠α = 45°, то:
H = 5⋅sin 45 ≈ 3,53 см
Если известны длина стороны а и угол β
Чему равна высота h равнобедренного треугольника если длина сторон, а угол
Чему равна высота H у равнобедренного треугольника если известны длина стороны A и угол Β?
Пример
Если сторона a = 5 см, а ∠β = 30°, то:
Если известны длина стороны b и угол α
Чему равна высота h равнобедренного треугольника если длина основания, а угол
Чему равна высота H у равнобедренного треугольника если известны длина стороны B и угол Α?
Пример
Если сторона b = 20 см, а ∠α = 35°, то:
Если известны длина стороны b и угол β
Чему равна высота h равнобедренного треугольника если длина основания, а угол
Чему равна высота H у равнобедренного треугольника если известны длина стороны B и угол Β?
Пример
Если сторона b = 15 см, а ∠β = 40°, то:
Примечание: треугольник называется Равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.
Если известны длина стороны а и основания b
Чему равна высота h равнобедренного треугольника если Длина сторон , а Длина основания
Чему равна высота H у равнобедренного треугольника если известны длина стороны A и длина основания B?
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
H = √ 10 2 — ( 5 /2) 2 = √ 100 — 6.25 ≈ 9.68 см
Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см. Найдите длину высоты, опущенной к основанию.
Свойства высоты в равнобедренном треугольнике
Третья сторона называется основанием.
09.02.2017 21:24:05
2017-02-09 21:24:05
Любые данныеЛюбые данные Любые данные Любые данные
Основные признаки
- Для успешного решения задач следует запомнить основные особенности равнобедренных треугольников. Они кажутся противоположными теоремам.
- Если при решении задачи обнаружено равенство двух углов, вы имеете дело с равнобедренным треугольником.
- Если вам удалось доказать, что медиана является также и высотой треугольника, смело делайте вывод, что треугольник равнобедренный.
- Если биссектриса также является высотой, то треугольник по основным признакам классифицируется как равнобедренный.
- И конечно, если в качестве высоты выступает еще и медиана, то такой треугольник равнобедренный.
Радиус вписанной окружности в равнобедренный треугольник
|
Обозначения в формулах, можно посмотреть на рисунке выше. Радиус вписанной окружности для равнобедренного треугольника можно найти, исходя из величин основания и каждой стороны. (Формула 1) Радиус вписанной окружности для равнобедренного треугольника можно определить,исходя из величин основания и высоты, проведенной к этому основанию (Формула 2) Радиус вписанной в равнобедренный треугольник окружности можно также вычислить через длину боковой стороны и высоту, проведенную к основанию треугольника (Формула 3) Знание величины угла между боковыми сторонами и длины основания также позволяет определить радиус вписанной окружности (Формула 4) Аналогичная формула (5) позволяет определить радиус вписанной окружности через боковые стороны и угол между ними |
Понятие равнобедренного треугольника
Введем для начала определение треугольника.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Определение 1
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Определение 2
Точки в рамках определения 1 называются вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 называются сторонами треугольника.
Введем теперь понятие равнобедренного треугольника.
Определение 4
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Определение 5
Равные стороны в рамках определения 4, будем называть боковыми, а третью – основанием (рис. 1).
Замечание 1
Отметим, что если боковые стороны равнобедренного треугольника также равняются его основанию, то треугольник будем называть равносторонним.
Признаки равнобедренной фигуры
Существует 4 явления, с помощью которых можно определить принадлежность тела к треугольникам. Все они сгруппированы в 3 теоремы:
- Если в треугольнике построить медиану, при этом она будет совпадать с высотой, он является равнобедренным. Аналогично можно утверждать о принадлежности фигуры к равнобедренному типу, когда биссектриса совпадает с высотой.
- Если 2 угла равны, треугольник равнобедренный.
- Если медиана и биссектриса совпадают, причём построены из одного угла, фигура называется равнобедренной.
Для доказательства первой теоремы нужно использовать признаки равенства треугольников. Если изобразить на чертеже фигуру ABC и из вершины B построить высоту, согласно заданным данным, она будет медианой или биссектрисой. В первом случае противоположная сторона будет разделена на 2 равные части AD и DC. Значит, треугольники ABD и DBC одинаковые. Отсюда следует, что у фигур есть равные стороны: AB = BC., то есть боковые грани имеют одинаковую длину, что и требуется по определению.
Доказательство второй теоремы следует построить на нахождении равных сторон. Для этого нужно отложить серединный перпендикуляр a и доказать, что линия будет проходить через вершину B. Если она не будет пересекать угол B, она касается AB или BC. Пусть точкой пересечения перпендикуляра будет M. Тогда по первому признаку AKM = CKM, значит, углы MCK и MAK также равны. По условию теоремы MCK = MAB → MAK = MAB, что противоречит аксиоме измерения углов. Отсюда можно утверждать, что серединный перпендикуляр не пересекает BC или AC. Значит, прямая проходит через вершину B.
Основные понятия
Как и любая наука, геометрия имеет свои основные правила и понятия. Их достаточно много. Рассмотрим лишь те, без которых наша тема будет несколько непонятна.
Высота — это прямая линия, проведенная перпендикулярно к противоположной стороне.
Медиана — это отрезок, направленный из любой вершины треугольника исключительно к середине противоположной стороны.
Биссектриса угла — это луч, разделяющий угол пополам.
Биссектриса треугольника — это прямая, вернее, отрезок соединяющий вершину с противоположной стороной.
Очень важно запомнить, что биссектриса угла — это обязательно луч, а биссектриса треугольника — это часть такого луча
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
| Равнобедренный треугольник – это треугольник, у которого две стороны равны. |
Давайте посмотрим на этот треугольник:
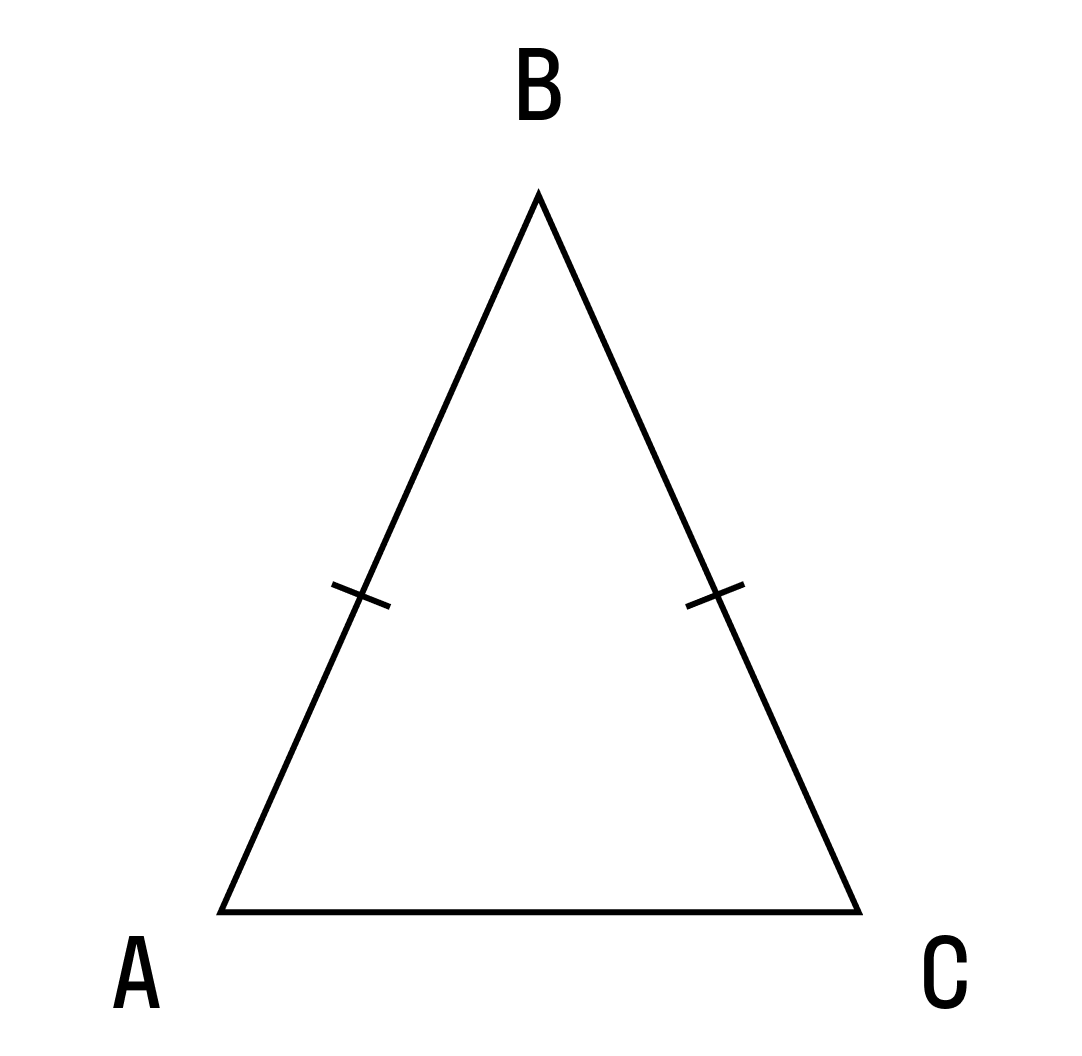
На рисунке хорошо видно, что стороны равны. Это подобие делает треугольник равнобедренным.
Как называются стороны равнобедренного треугольника:
АВ и ВС — стороны,
АС — основание треугольника.
Для понимания материала нам нужно вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — это луч, выходящий из вершины угла и делящий этот угол на два равных угла.
Даже если вы не знаете определения, вы наверняка слышали о крысе, которая бегает по углам и раскалывает их пополам. Она не даст вам забыть, что такое биссектриса. А если не любишь крыс, то бегать может кто угодно. Биссектриса — это кот. Полушарнир — лиса. Для фэнтези нет правил. Все правила относятся к геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектриса будет отрезком BH
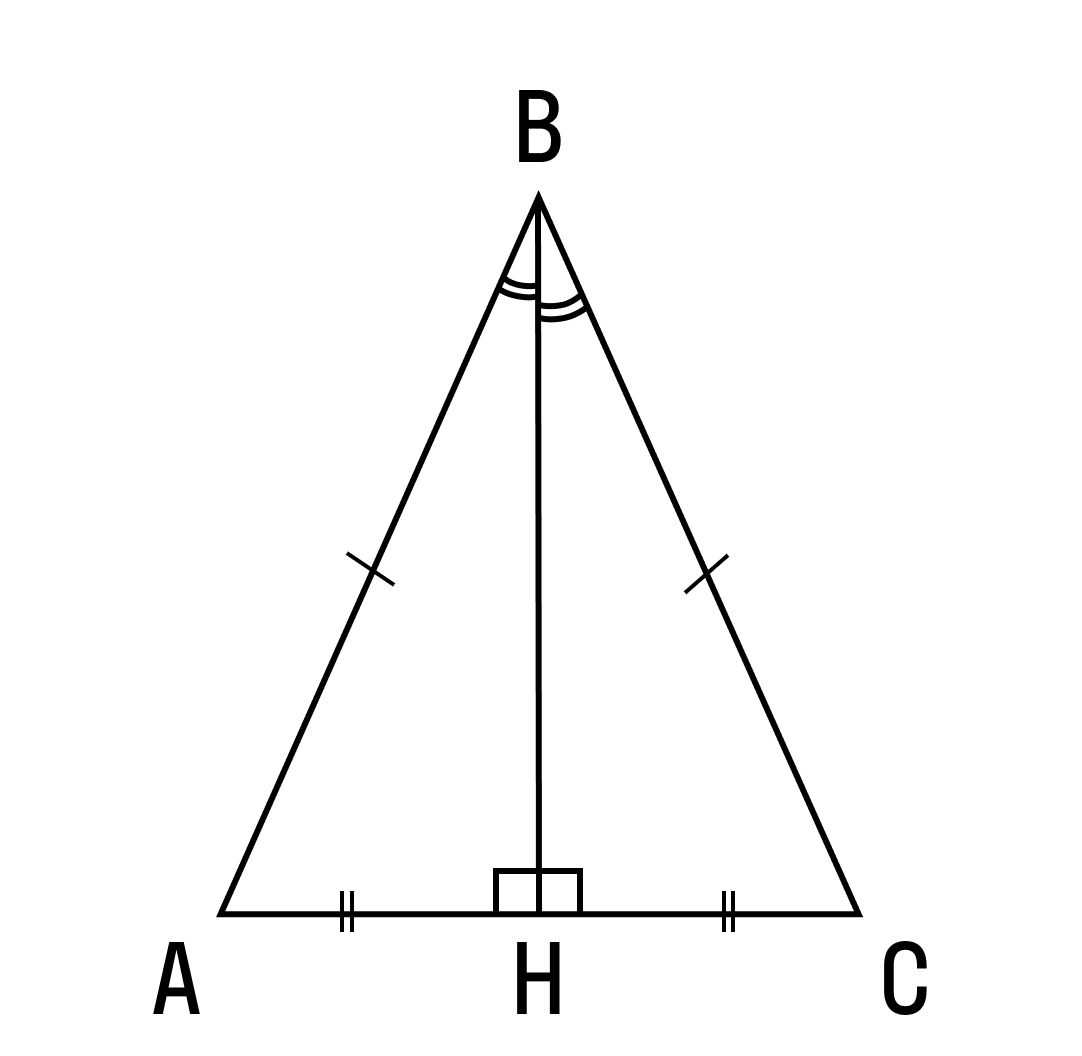
Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Для медианы не придумали забавного правила, как с биссектрисой, но можно придумать. Например, буддийское воспоминание: «Средний — это лама, блуждающий от вершины треугольника к середине основания и обратно».
В этом треугольнике медианой является отрезок BH.
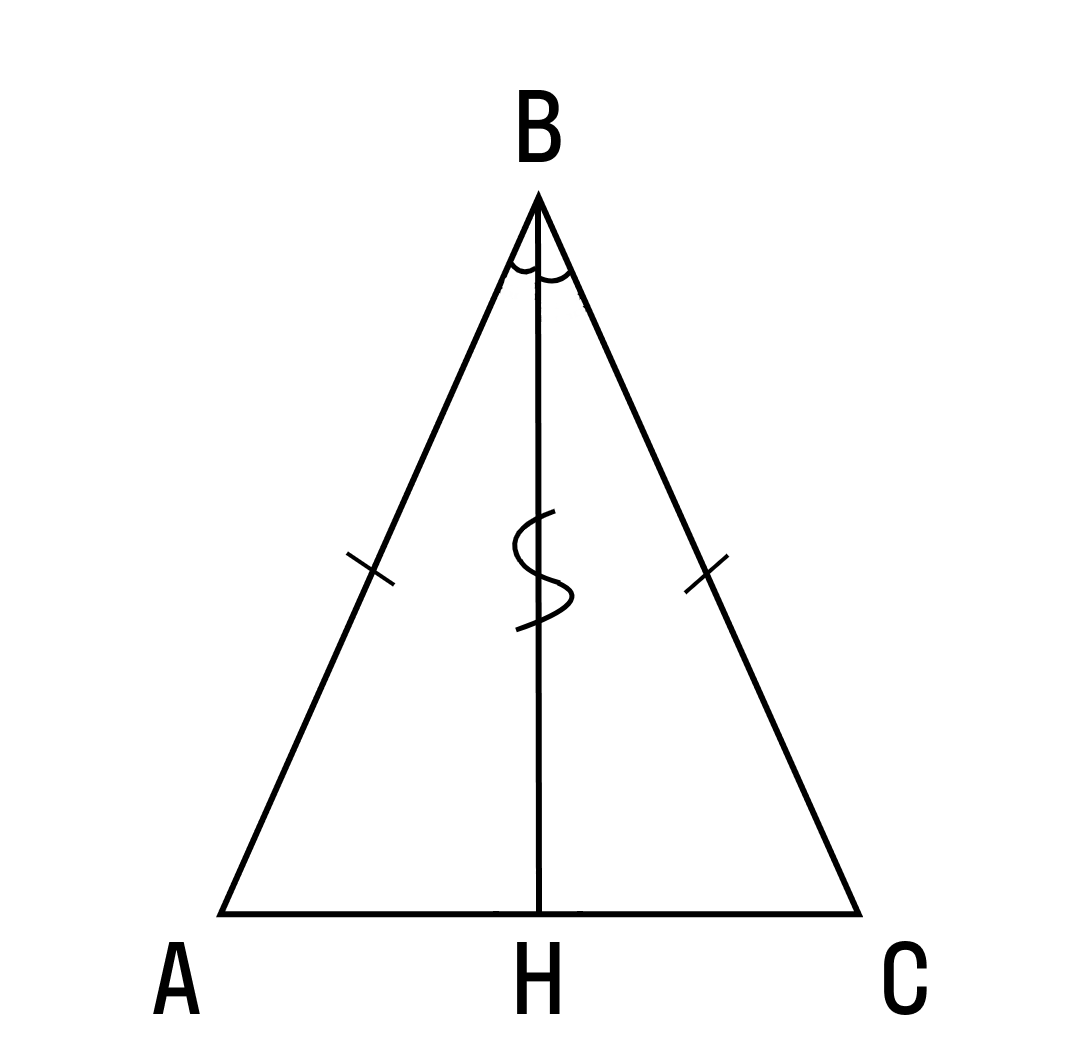
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высота в представленном равнобедренном треугольнике – это отрезок BH.
Равнобедренный треугольник, свойства, признаки и формулы
- Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
- Равнобедренный треугольник (понятие)
- Свойства равнобедренного треугольника
- Признаки равнобедренного треугольника
- Формулы равнобедренного треугольника
- Прямоугольный треугольник, равносторонний треугольник
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.
Рис. 1. Равнобедренный треугольник
- АВ = ВС – боковые стороны, АС – основание,
- ∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
- По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
- Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
- Различают следующие виды равнобедренных треугольников:
- – остроугольный – все углы острые;
- – прямоугольный – угол при вершине прямой, а при основании углы острые;
- – тупоугольный – угол при вершине тупой, а при основании углы острые;
- – равносторонний (или правильный) – все стороны равны и все углы равны.
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.
Рис. 2. Равнобедренный треугольник
∠ BАC = ∠ BСA
2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.
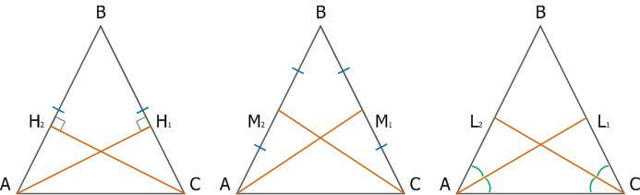
Рис. 3. Равнобедренный треугольник
АН1 = СН2 – высота, АМ1 = СМ2 – медиана, АL1 = СL2 – биссектриса, проведённые из углов при основании
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Рис. 4. Равнобедренный треугольник
ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок
4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.
Рис. 5. Равнобедренный треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
Признаки равнобедренного треугольника:
- – если в треугольнике два угла равны, то он равнобедренный;
- – если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
- – если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
- – если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Формулы равнобедренного треугольника:
Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).
Рис. 6. Равнобедренный треугольник
- Формулы длины основания (b):
- ,
- ,
- .
- Формулы длины равных сторон (а):
- .
- Формулы углов:
Рис. 7. Равнобедренный треугольник
- ,
- ,
- .
- Формулы периметра (Р) равнобедренного треугольника:
Рис. 8. Равнобедренный треугольник
- ,
- .
- Формулы площади (S) равнобедренного треугольника:
- ,
- ,
- .
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Примечание: Фото https://www.pexels.com, https://pixabay.com
карта сайта
Задача #1
На рисунке изображен $\bigtriangleup{ABC}$, где $BC=CA$. Известно, что $\angle{1}=130^{\circ}$. Чему равняется значение угла $\angle{2}$?
Дано:$\bigtriangleup{ABC}$$BC=CA$$\angle{1}=130^{\circ}$
Найти: $\angle{2}~—~?$
РешениеРассмотрим $\bigtriangleup{ABC}$. В нем по условию боковые стороны $BC$ и $CA$ равны. Следовательно $\bigtriangleup{ABC}$ — равнобедренный треугольник, по определению равнобедренного треугольника.
Угол $\angle{1}$ — смежный угол с $\angle{ABC}$. Сумма смежных углов равняется $180^{\circ}$, откуда получаем значение $\angle{ABC}=180^{\circ}-130^{\circ}=50^{\circ}.$ По теореме о равнобедренном треугольнике, углы при основании равнобедренных треугольников равны. Тогда $\angle{ABC}=\angle{CAB}$.
Угол $\angle{2}$ — вертикальный угол с $\angle{CAB}$. По теореме о равенстве вертикальных углов получаем, что $\angle{CAB}=\angle{2}=\angle{ABC}=50^{\circ}.$
Ответ: $50^{\circ}.$
Свойства и признаки равнобедренного треугольника
| О нас |
| Демоверсии |
| Учебные пособия |
| Справочник по математике |
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство | Углы при основании равнобедренного треугольника | Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак | Высота треугольника, совпадающая с медианой | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак | Высота треугольника, совпадающая с биссектрисой | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак | Биссектриса треугольника, совпадающая с медианой | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
| Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство: углы при основании равнобедренного треугольника | |
| Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак: два равных угла треугольника | |
| Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
| В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак: высота треугольника, совпадающая с медианой | |
| Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак: высота треугольника, совпадающая с биссектрисой | |
| Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак: биссектриса треугольника, совпадающая с медианой | |
| Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение равнобедренного треугольника |
|
| Свойство углов при основании равнобедренного треугольника |
| Свойство:Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
| Признак:Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
| Свойство:В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
| Признак:Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
| Признак:Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
| Признак:Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.