Формула для вычисления объема правильного тетраэдра

Тетраэдры в микромире

• Правильный тетраэдр образуется при sp 3 -гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника
• Молекула метана СН 4
• Сульфат-ион SO 4 2- , фосфат-ион PO 4 3- , перхлорат-ион ClO 4 — и многие другие ионы
• Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем
• Флюорит CaF 2 , тетраэдр с ребром равным 3, 8626 ангстрем
• Сфалерит , ZnS, тетраэдр с ребром равным 3,823 ангстрем
• Комплексные ионы — , 2- , 2- , 2+
• Силикаты , в основе структур которых лежит кремнекислородный тетраэдр 4-

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра
Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Примечание
. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение
Для простых подкоренных выражений может использоваться знак «√»
Правильный тетраэдр

У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

У тетраэдра 4 грани, 4 вершины и 6 ребер.

Основные формулы для правильного тетраэдра приведены в таблице.

Где:

S — Площадь поверхности правильного тетраэдра

V — объем

h — высота, опущенная на основание

r — радиус вписанной в тетраэдр окружности

R — радиус описанной окружности

a — длина ребра

10 Как узнать объём прямоугольной тары

В сфере строительства все показатели объёма приведены к конкретным величинам. Расчёты могут проводиться в литрах или дм 3 , но чаще всего для определения количества того или иного материала используются кубические метры. Как рассчитать кубатуру самых простых прямоугольных ёмкостей опишем дальше на конкретном примере.

Для работы нам понадобится тара, строительная рулетка и блокнот с ручкой или карандашом для проведения вычислений. Из курса геометрии известно, что объём подобных тел вычисляется умножением длины, ширины и высоты изделия. Формула расчётов сводится к следующему

V=a*b*c, где a, b и с – стороны тары.

Например, длина нашего изделия равняется 150 сантиметрам, ширина 80 сантиметрам, высота 50 сантиметров. Для правильного подсчёта кубатуры указанные величины переводим в метры и проводим необходимые расчёты V=1,5*0,8*0,5=0,6м3.

Формулы объема тетраэдра

О±ÃÂõü ôðýýþóþ ÃÂõûð üþöýþ ýðùÃÂø ýõÃÂúþûÃÂúøüø ÃÂÿþÃÂþñðüø. àð÷ñõÃÂõü øàñþûõõ ÿþôÃÂþñýþ.

ÃÂÃÂûø ÃÂõÃÂÃÂðÃÂôàÿþÃÂÃÂÃÂþõý ýð ÃÂÃÂõàòõúÃÂþÃÂðààúþþÃÂôøýðÃÂðüø:

ÃÂþóôð þñÃÂõü ÃÂÃÂþóþ ÃÂõÃÂÃÂðÃÂôÃÂð ÃÂÃÂþ ÃÂüõÃÂðýýþõ ÿÃÂþø÷òõôõýøõ ÃÂÃÂøàòõúÃÂþÃÂþò, ÃÂþ õÃÂÃÂàÃÂðúþù þÿÃÂõôõûøÃÂõûÃÂ:

Формула вычисления объема тетраэдра

1. Общая формула (через площадь основания и высоту)

Объем (V) тетраэдра считается также, как и объем любой пирамиды. Он равняется одной третьей произведения площади любой грани и высоты, опущенной на нее:

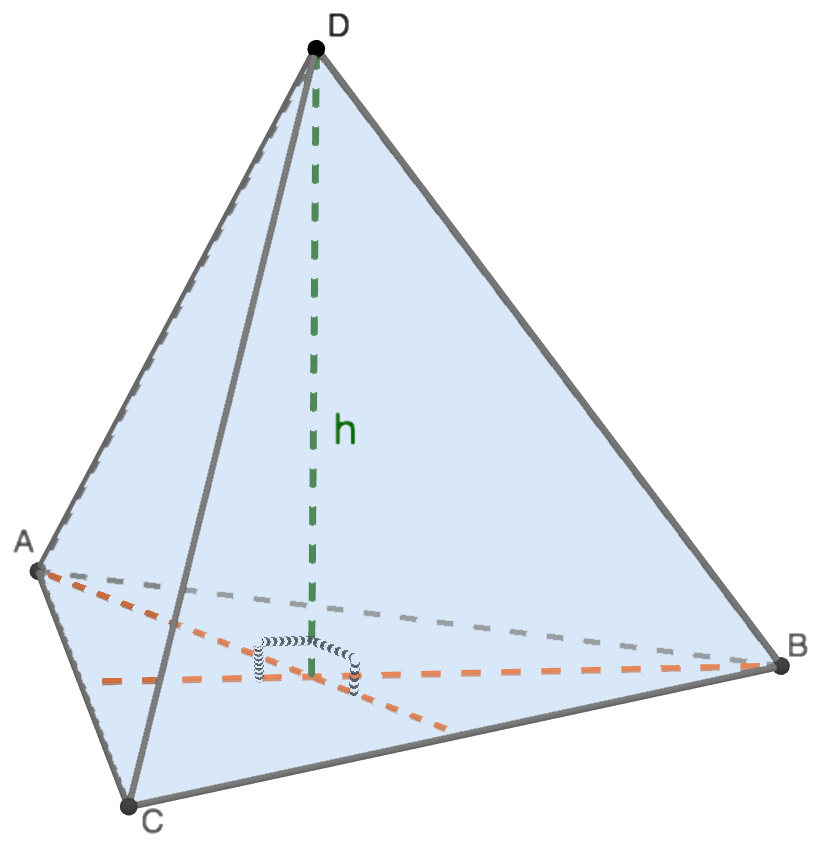
• S – площадь грани ABC, в данном случае выступающего в роли основания
• h – высота, опущенная на грань ABC

2. Объем правильного тетраэдра

В правильном тетраэдре все грани являются равносторонними треугольниками. Объем данной фигуры равен одной двенадцатой произведения длины его ребра в кубе на квадратный корень из числа 2.

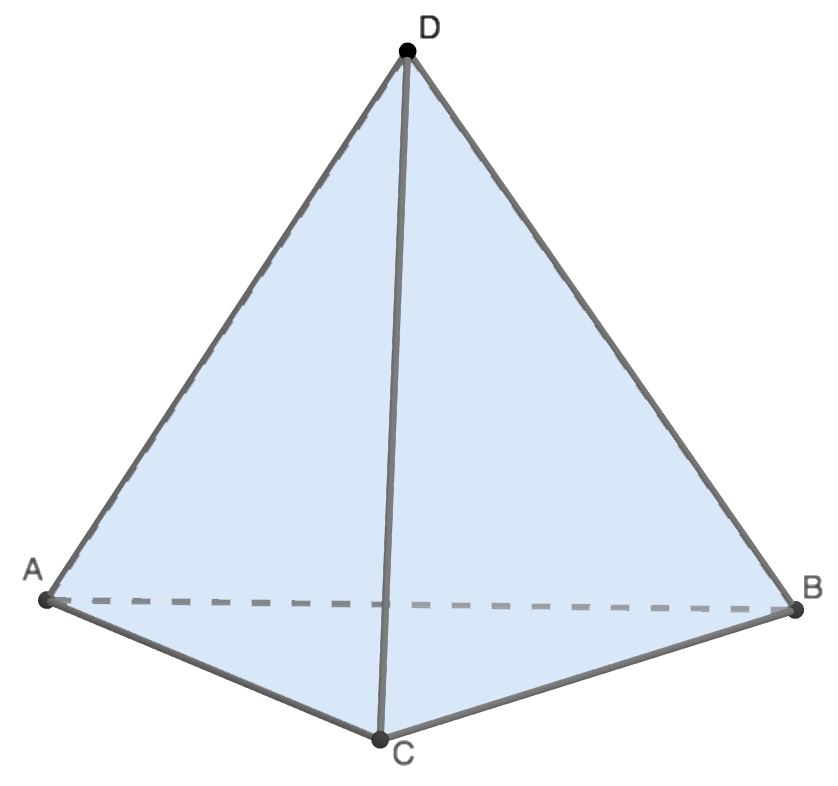
Т.к. это правильный тетраэдр, все его ребра равны (AB = BC = AC = AD = BD = CD).

Практические примеры

Задача
Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3

Решение
.

Поскольку все ребра треугольной пирамиды равны — она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a 2 √3 .

Тогда

S = 3√3

Ответ
: 3√3

Задача
.

Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды

Решение
.

Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания, который одновременно является центром описанной окружности, то

AO = R = √3 / 3 a

AO = 4√3 / 3

Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM

AO 2 + OM 2 = AM 2

OM 2 = AM 2 — AO 2

OM 2 = 4 2 — (4√3 / 3) 2

OM 2 = 16 — 16/3

OM = √(32/3)

OM = 4√2 / √3

Объем пирамиды найдем по формуле V = 1/3 Sh

При этом площадь основания найдем по формуле S = √3/4 a 2

V = 1/3 (√3 / 4 * 16) (4√2 / √3)

V = 16√2 / 3

Ответ
: 16√2 / 3 см

Определение тетраэдра

Тетраэдр
– простейшее многогранное тело, гранями и основанием которого являются треугольники.

Определение геометрических тел

Один из разделов геометрии — стереометрия — изучает самые разнообразные пространственные фигуры и их свойства. В общем случае геометрическое тело — это часть пространства, имеющая наружные границы в виде замкнутой поверхности. Сугубо геометрическое определение описывает любую пространственную форму как компактную совокупность множества точек, каждые две из которых можно соединить отрезком и он будет полностью находиться внутри заданного ограниченного контура.

Совокупность всех точек, которые находятся на границе тела, составляет его поверхность. Кроме того, можно сказать, что любое геометрическое тело образовано множеством внутренних точек. В

иды пространственных фигур:

• многогранники;
• тела вращения.

Конечное число плоских многоугольников, ограничивающих пространственное тело, называется многогранником. При этом должны соблюдаться два свойства:

1. Любая сторона каждого из многоугольников одновременно является стороной другого многоугольника и только их двоих. Соприкасающиеся стороны называются смежными.
2. Все многоугольники связаны между собой — от каждого из них можно проложить путь до любого другого через смежные стороны.

В геометрии многоугольники, образующие сложный пространственный многогранник, называют гранями, отрезки, образованные местом соединения двух смежных граней — ребрами, а углы, образованные соединенными в одной точке гранями — вершинами.

Общий принцип названий таких геометрических тел заключается в указании количества их сторон.

Таким образом, если число граней обозначить n, то название образуется как n-гранник:

• 4 грани — четырехгранник;
• 5 граней — пятигранник;
• 6 граней — шестигранник;
• 8 граней — восьмигранник.

Если весь многогранник находится только с одной стороны каждой своей грани, то его называют выпуклым, в противном случае — вогнутым или невыпуклым. Звездчатые многогранники, состоящие из множества правильных пространственных фигур, относятся к невыпуклым.

Объем прямоугольного параллелепипеда

Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.

Рисунок 5.

Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.

Объем измеряется с помощью следующих единиц:

$мм^3$ — миллиметр кубический,

$см^3$ — сантиметр кубический,

$дм^3$ — дециметр кубический,

$м^3$ — метр кубический,

$км^3$ — километр кубический.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Виды тетраэдра

Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:

• правильным, то есть в основании равносторонний треугольник;
• равногранным, у которого все грани одинаковы по длине;
• ортоцентрическим, когда высоты имеют общую точку пересечения;
• прямоугольным, если плоские углы при вершине нормальные;
• соразмерным, все би высоты равны;
• каркасным, если присутствует сфера, которая касается ребер;
• инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.

Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.

Исходя из названия, можно понять, что так он называется потому, что грани являют собой правильные треугольники. Все ребра этой фигуры конгруэнтны по длине, а грани — по площади. Правильный тетраэдр — это один из пяти аналогичных многогранников.

Как начертить пирамиду в прямоугольной системе координат?

14) Выполним точный чертёж пирамиды  прямоугольной системе координат. Это проще, чем кажется.

С чего начать?

Во-первых, необходимо уметь правильно изображать саму систему координат на клетчатой бумаге. Справка в начале методички Графики и свойства функций.

Во-вторых, необходимо уметь строить точки в трёхмерном пространстве, об этом я уже начал рассказывать в статье Уравнения прямой в пространстве. И сейчас мы продолжим тему.

Построим точку . На мой взгляд, сначала удобно разобраться с первыми двумя координатами – «иксом» и «игреком»: отмеряем 2 единицы в положительном направлении оси  и 3 единицы в отрицательном направлении оси . В плоскости  прочерчиваем пунктирные дорожки, которые параллельны соответствующим  координатным осям. Пересечение дорожек я пометил небольшим ромбиком:

Теперь, в соответствии с отрицательной «зетовой» координатой, отмеряем 1 единицу вниз и тоже проводим пунктирную дорожку. Здесь и будет находиться наша точка , она расположена в нижнем полупространстве.

Для точки  отмеряем 5 единиц «на себя» и 4 единицы вправо, строим параллельные осям пунктирные дорожки и находим их точку пересечения. В соответствии с «зетовой» координатой, чертим пунктиром «подставку для точки» – 2 единицы вверх. Данная точка расположена в верхнем полупространстве.

Аналогично строятся две другие точки. Заметьте, что вершина  лежит в самой плоскости .

В тетради пунктирные линии аккуратно и не жирно проводятся простым карандашом.

Теперь нужно разобраться в удалённости точек, а в этом как раз и помогут пунктирные линии. Немного включаем пространственное воображение и внимательно смотрим на ось . Очевидно, что самая близкая к нам вершина – , а самая удалённая – .

Немало читателей уже мысленно прорисовали пирамиду, тем не менее, остановлюсь на построении подробнее. После того, как построены вершины, чайники могут тонко-тонко карандашом начертить все 6 сторон, и начинать разбираться, какие рёбра видимы, а какие рёбра скрыты. Лучше начать от самой близкой точки . Очевидно, что все три «исходящих» ребра в поле нашего зрения: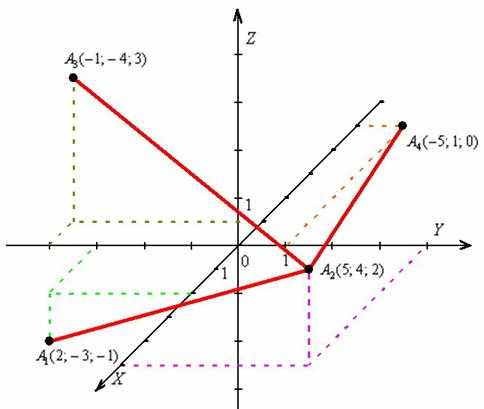

Должен предостеречь, так бывает далеко не всегда, одно ребро, например, может быть от нас скрыто. Не теряйте визуального восприятия пространства!

Какие ещё стороны в зоне видимости? ВиднЫ рёбра , а вот сторона  спряталась за пирамидой: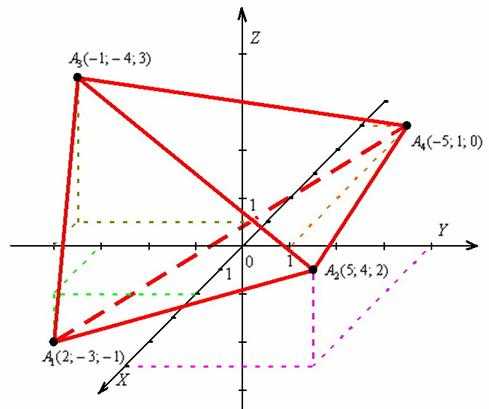

К слову, невидимое нам ребро  лежит в нижнем полупространстве и проходит под осями .

Чертеж-конфетка на практике получается не во всех случаях. Бывает, фортуна разворачивается и задом:

То есть, грань пирамиды может полностью или частично закрывать всё остальное. Но самое скверное, когда перекрываются рёбра: 
Тут сразу три ребра выстроились на одной прямой (правая верхняя прямая). В похожей ситуации приходится жирно прочерчивать накладывающиеся стороны разными цветами и ниже чертежа записывать дополнительные комментарии о расположении пирамиды.

Существуют и более мелкие неприятности, например, одна из сторон пирамиды может наложиться на координатную ось (а то и вовсе расположиться за ней).

Увы, перечисленные случаи – не редкость на практике.

Вот, пожалуй, и все основные сведения о построении треугольной пирамиды в декартовой системе координат.

15) Это пример для самостоятельного решения.

В конце решения желательно остограммиться записать ответ, и по пунктам перечислить полученные результаты. За ваше здоровье!

(Переход на главную страницу)

Как определить площадь сечения цилиндра, конуса, призмы и пирамиды? Формулы

На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.

Объемные фигуры

Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Вам будет интересно: Что значит слыть: толкование, синонимы

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.

Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).

Цилиндр

Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:

• круглое;
• прямоугольное;
• эллиптическое.

Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.

Площадь круглого сечения рассчитывается по формуле:

Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:

Сечения конуса

Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:

• круглое;
• эллиптическое;
• параболическое;
• гиперболическое;
• треугольное.

Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.

Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:

Формулы объема правильной треугольной пирамиды

Правильная пирамида треугольная имеет равносторонний треугольник в основании. Известно, что высота этого треугольника связана с длиной его стороны равенством:

ho = √3/2*a.

Подставляя это выражение в формулу для объема треугольной пирамиды, записанную в предыдущем пункте, получаем:

V = 1/6*a*ho*h = √3/12*a2*h.

Объем правильной пирамиды с треугольным основанием является функцией длины стороны основания и высоты фигуры.

Поскольку любой правильный многоугольник можно вписать в окружность, радиус которой однозначно определит длину стороны многоугольника, тогда эту формулу можно записать через соответствующий радиус r:

V = √3/4*h*r2.

Эту формулу легко получить из предыдущей, если учесть, что радиус r описанной окружности через длину стороны a треугольника определяется выражением:

r = a/√3.

Задача с гомотетичными пирамидами

Решим одну любопытную геометрическую задачу. Предположим, что имеется треугольная правильная пирамида с некоторым объемом V1. Во сколько раз следует уменьшить размеры этой фигуры, чтобы получить гомотетичную ей пирамиду с объемом, в три раза меньшим исходного?

Задачу начнем решать с записи формулы для исходной правильной пирамиды:

V1 = √3/12*a12*h1.

Пусть необходимый по условию задачи объем фигуры получится, если умножить ее параметры на коэффициент k. Имеем:

V2 = √3/12*k2*a12*k*h1 = k3*V1.

Поскольку из условия известно отношение объемов фигур, то получаем значение коэффициента k:

k = ∛(V2/V1) = ∛(1/3) ≈ 0,693.

Отметим, что аналогичное значение коэффициента k мы бы получили для пирамиды произвольного типа, а не только для правильной треугольной.

Формулы объема тетраэдра

Объем данного тела можно найти несколькими способами. Разберем их более подробно.

Через смешанное произведение векторов

Если тетраэдр построен на трех векторах с координатами:

тогда объем этого тетраэдра это смешанное произведение этих векторов, то есть такой определитель:

Объем тетраэдра через определитель

V = 1 6 ⋅ ∣ a x a y a z b x b y b z c x c y c z ∣ V=\frac{1}{6}\cdot\begin{vmatrix}
a_x & a_y & a_z \\
b_x & b_y & b_z \\
c_x & c_y & c_z \\
\end{vmatrix}
V
=

6

1

​

⋅

∣

∣

∣

∣

∣

∣

​

a
x

​

b
x

​

c
x

​

​

a
y

​

b
y

​

c
y

​

​

a
z

​

b
z

​

c
z

​

​

∣

∣

∣

∣

∣

∣

​

Известны координаты четырех вершин октаэдра. A (1 , 4 , 9) A(1,4,9)
A
(1
,
4
,
9
)

, B (8 , 7 , 3) B(8,7,3)
B
(8
,
7
,
3
)

, C (1 , 2 , 3) C(1,2,3)
C
(1
,
2
,
3
)

, D (7 , 12 , 1) D(7,12,1)
D
(7
,
1
2
,
1
)

. Найдите его объем.

Решение

A (1 , 4 , 9) A(1,4,9)
A
(1
,
4
,
9
)

B (8 , 7 , 3) B(8,7,3)
B
(8
,
7
,
3
)

C (1 , 2 , 3) C(1,2,3)
C
(1
,
2
,
3
)

D (7 , 12 , 1) D(7,12,1)
D
(7
,
1
2
,
1
)

Первым шагом является определение координат векторов, на которых построено данное тело.
Для этого необходимо найти каждую координату вектора путем вычитания соответствующих координат двух точек. Например, координаты вектора A B → \overrightarrow{AB}
A
B

, то есть, вектора, направленного от точки A A
A

к точке B B
B

, это разности соответствующих координат точек B B
B

и A A
A

A B → = (8 − 1 , 7 − 4 , 3 − 9) = (7 , 3 , − 6) \overrightarrow{AB}=(8-1, 7-4, 3-9)=(7, 3, -6)
A
B

=

(8
−

1
,
7
−

4
,
3
−

9
)
=

(7
,
3
,
−
6
)

A C → = (1 − 1 , 2 − 4 , 3 − 9) = (0 , − 2 , − 6) \overrightarrow{AC}=(1-1, 2-4, 3-9)=(0, -2, -6)
A
C

=

(1
−

1
,
2
−

4
,
3
−

9
)
=

(0
,
−
2
,
−
6
)

A D → = (7 − 1 , 12 − 4 , 1 − 9) = (6 , 8 , − \overrightarrow{AD}=(7-1, 12-4, 1-9)=(6, 8, -8)
A
D

=

(7
−

1
,
1
2
−

4
,
1
−

9
)
=

(6
,
8
,
−
8
)

Теперь найдем смешанное произведение данных векторов, для этого составим определитель третьего порядка, при этом принимая, что A B → = a ⃗ \overrightarrow{AB}=\vec{a}
A
B

=

a

, A C → = b ⃗ \overrightarrow{AC}=\vec{b}
A
C

=

b

, A D → = c ⃗ \overrightarrow{AD}=\vec{c}
A
D

=

c

.

∣ a x a y a z b x b y b z c x c y c z ∣ = ∣ 7 3 − 6 0 − 2 − 6 6 8 − 8 ∣ = 7 ⋅ (− 2) ⋅ (− + 3 ⋅ (− 6) ⋅ 6 + (− 6) ⋅ 0 ⋅ 8 − (− 6) ⋅ (− 2) ⋅ 6 − 7 ⋅ (− 6) ⋅ 8 − 3 ⋅ 0 ⋅ (− = 112 − 108 − 0 − 72 + 336 + 0 = 268 \begin{vmatrix}
a_x & a_y & a_z \\
b_x & b_y & b_z \\
c_x & c_y & c_z \\
\end{vmatrix}=
\begin{vmatrix}
7 & 3 & -6 \\
0 & -2 & -6 \\
6 & 8 & -8 \\
\end{vmatrix}=7\cdot(-2)\cdot(-8) + 3\cdot(-6)\cdot6 + (-6)\cdot0\cdot8 — (-6)\cdot(-2)\cdot6 — 7\cdot(-6)\cdot8 — 3\cdot0\cdot(-8) = 112 — 108 — 0 — 72 + 336 + 0 = 268
∣

∣

∣

∣

∣

∣

​

a
x

​

b
x

​

c
x
​
​
a
y
​
b
y
​
c
y
​
​
a
z
​
b
z
​
c
z
​
​
∣

∣

∣

∣

∣

∣

​
=
∣

∣

∣

∣

∣

∣

​
7
6
​
3
−
2
8
​
−
6
−
6
−
8
​
∣

∣

∣

∣

∣

∣

​
=
7
⋅
(−
2
)
⋅
(−
8
)
+
3
⋅
(−
6
)
⋅
6
+
(−
6
)
⋅
⋅
8
−
(−
6
)
⋅
(−
2
)
⋅
6
−
7
⋅
(−
6
)
⋅
8
−
3
⋅
⋅
(−
8
)
=
1
1
2
−
1
8
−
−
7
2
+
3
3
6
+
=
2
6
8

То есть, объем тетраэдра равен:

V = 1 6 ⋅ ∣ a x a y a z b x b y b z c x c y c z ∣ = 1 6 ⋅ ∣ 7 3 − 6 0 − 2 − 6 6 8 − 8 ∣ = 1 6 ⋅ 268 ≈ 44.8 см 3 V=\frac{1}{6}\cdot\begin{vmatrix}
a_x & a_y & a_z \\
b_x & b_y & b_z \\
c_x & c_y & c_z \\
\end{vmatrix}=\frac{1}{6}\cdot
\begin{vmatrix}
7 & 3 & -6 \\
0 & -2 & -6 \\
6 & 8 & -8 \\
\end{vmatrix}=\frac{1}{6}\cdot268\approx44.8\text{ см}^3
V
=
6
1
​
⋅
∣

∣

∣

∣

∣

∣

​
a
x
​
b
x
​
c
x
​
​
a
y
​
b
y
​
c
y
​
​
a
z
​
b
z
​
c
z
​
​
∣

∣

∣

∣

∣

∣

​
=
6
1
​
⋅
∣

∣

∣

∣

∣

∣

​
7
6
​
3
−
2
8
​
−
6
−
6
−
8
​
∣

∣

∣

∣

∣

∣

​
=
6
1
​
⋅
2
6
8
≈
4
4
.
8
см
3

Ответ

44.8 см 3 . 44.8\text{ см}^3.
4
4
.
8
см
3
.

Формула объема равногранного тетраэдра по его стороне

Эта формула справедлива только для вычисления объема равногранного тетраэдра, то есть такого тетраэдра, у которого все грани являются одинаковыми правильными треугольниками.

Объем равногранного тетраэдра

V = 2 ⋅ a 3 12 V=\frac{\sqrt{2}\cdot a^3}{12}
V
=
1
2
2
​
⋅
a
3
​

a a
a
— длина ребра тетраэдра.

Определить объем тетраэдра, если дана его сторона, равная 11 см 11\text{ см}
1
1
см
.

Решение

a = 11 a=11
a
=
1
1

Подставляем a a
a
в формулу для объема тетраэдра:

V = 2 ⋅ a 3 12 = 2 ⋅ 1 1 3 12 ≈ 156.8 см 3 V=\frac{\sqrt{2}\cdot a^3}{12}=\frac{\sqrt{2}\cdot 11^3}{12}\approx156.8\text{ см}^3
V
=
1
2
2
​
⋅
a
3
​
=
1
2
2
​
⋅
1
1
3
​
≈
1
5
6
.
8
см
3

Ответ

156.8 см 3 . 156.8\text{ см}^3.
1
5
6
.
8
см
3
.

Объем конуса

Рассмотрим конус с высотой h и радиусом основания R. Совместим начало координат с вершиной конуса и направим ось Ох в сторону основания конуса. Тогда она пересечет основание в какой-то точке М c координатой h. Далее через точку М₁ на оси Ох, имеющей координату х, проведем сечение, перпендикулярное оси Ох. Это сечение будет окружностью.

Также построим образующую ОА, которая будет проходить через сечение в точке А₁. Теперь сравним ∆ОАМ и ∆ОА₁М₁. Они прямоугольные, и у них есть общий угол ∠АОМ. Это значит, что они подобны, и поэтому справедливо отношение:

Полученную формулу можно переписать в другом виде так, чтобы она содержала площадь основания, причем она будет похожа на аналогичную формулу для пирамиды:

Задание. Радиус конуса – 8 см, а его высота составляет 12 см. Определите его объем.

Решение. Здесь надо просто применить выведенную формулу:

Задание. В сосуде, имеющем форму перевернутого конуса, вода доходит до уровня, соответствующего 2/3 высоты сосуда. При этом ее объем составляет 192 мл. Каков объем всего сосуда?

Решение. В задаче фигурируют два конуса. Один из них – это сам сосуд, а второй – его часть, заполненная водой. При выведении формулы объема мы уже выяснили, что радиусы таких конусов пропорциональны их высотам:

Мы уже заметили, что формулы для объема пирамида и конуса идентичны. По сути, конус можно рассматривать как особый случай пирамиды, у которой в основании лежит не многоугольник, а окружность. Аналогично и усеченный конус можно считать особым случаем усеченной пирамиды, а поэтому для расчета его объема можно применять такую же формулу:

Задание. Вычислите объем усеченного конуса с высотой 9 и радиусами оснований 7 и 4.

Решение. Сначала находим площади оснований:

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

• Все грани равны.
• Все плоские углы правильного тетраэдра равны 60°
• Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
• Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a. DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD.
Высота BM равна BM и равна

BDMDHMB

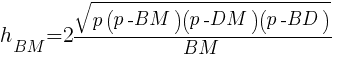
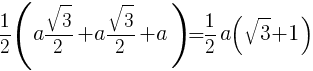
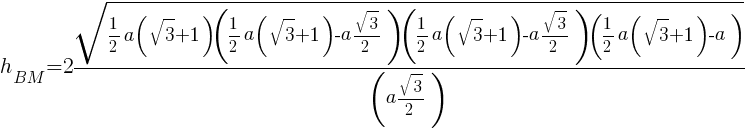
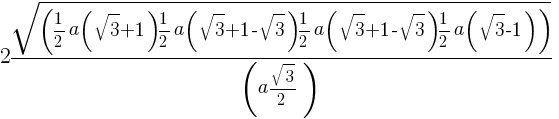
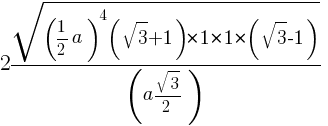
Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

11 Как определить объём сферического изделия

Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.

Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:

• V – подсчитываемый объём детали;
• R- радиус сферы;
• ԉ – постоянная величина, которая равняется 3,14.

Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.

А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу: