Ломаная линия

Виды матриц, какие бывают

В математике существует несколько видов матриц в зависимости от их размера.

1. Матрица–строка. Имеет размер 1×n, т.е. состоит из одной строки и нескольких столбцов.\(\begin{vmatrix}54&2&-7&0&4\end{vmatrix}\)
2. Матрица–столбец. Имеет размер m×1, т.е. состоит из одного столбца и нескольких строк.\(\begin{vmatrix}3\\-6\\64.5\end{vmatrix}\)

Также различают матрицы по значениям их элементов.

1. Нулевая матрица. Все элементы матрицы равны 0.\(\begin{vmatrix}0&0&0\\0&0&0\end{vmatrix}\)
2. Квадратная матрица. Количество строк и столбцов одинаковое: m=n.\(\begin{vmatrix}4&5&1\\5&0&0\\-2&2&-8\end{vmatrix}\)
3. Диагональная матрица — разновидность квадратной матрицы, у которой все элементы равны 0, за исключением диагональных элементов.\(\begin{vmatrix}3&0&0\\0&-8&0\\0&0&1.5\end{vmatrix}\)
4. Единичная матрица — разновидность диагональной матрицы. На главной диагонали расположены 1, а все остальные элементы равны 0. Обозначается латинской буквой E.\(\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}\)
5. Треугольная матрица. Имеет 2 разновидности: верхняя и нижняя. У верхней треугольной матрицы равны 0 элементы под главной диагональю, а у нижней треугольной матрицы — над главной диагональю.\(A=\begin{vmatrix}4&1.5&-2\\0&1&7\\0&0&4\end{vmatrix}\)

Треугольная матрица всегда квадратная: m=n.

6. Противоположная матрица. Обозначается -A и всегда рассматривается в отношении матрицы A. Ее элементы имеют обратный знак от элементов матрицы A.
7. Кососимметрическая (антисимметричная) матрица. Отличается множителем -1. Т.е. все элементы матрицы A были умножены на -1 и получилась матрица AT, или транспонированная матрица.\(A=\begin{vmatrix}0&5&217\\-5&0&-43\\-217&43&0\end{vmatrix},\;A^T=\begin{vmatrix}0&-5&-217\\5&0&43\\217&-43&0\end{vmatrix}\)

Кососимметрическая матрица всегда квадратная.

8. Симметрическая матрица. Элементы лежат симметрично по отношению к главной диагонали. Матрица всегда квадратная.\(A=\begin{vmatrix}1&3&0\\3&2&6\\0&6&5\end{vmatrix}\)
9. Трапециевидная матрица. Есть ряд условий, при которых матрица становится такого вида. Например, она должна быть квадратной или прямоугольной, при этом количество столбцов обязательно больше числа строк. Также элементы, расположенные над главной диагональю, не равны 0, а элементы под главной диагональю равны 0.\(A=\begin{vmatrix}1&2&3&4&5&6\\0&-1&0&7&-3&2\\0&0&4&1&-1&-2\end{vmatrix}\)

Отрезок в геометрии

Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. При этом сама точка в геометрии является абстрактным объектом, не имеющим никакой длины и вообще каких-либо измеряемых характеристик. Отрезок прямой, соединяющий две точки и (которые называются Концами отрезка), обозначается следующим образом — . Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок ». Любая точка, лежащая между концами отрезка, называется его Внутренней точкой. Расстояние между концами отрезка называют его Длиной и обозначают как.

Отрезок числовой (координатной) прямой (Числовой отрезок, Сегмент) — множество вещественных чисел, удовлетворяющих неравенству, где заранее заданные вещественные числа и называются Концами (Граничными точками) отрезка. В противоположность им, остальные числа, удовлетворяющие неравенству, называются Внутренними точками отрезка.

Отрезок обычно обозначается :

\mid a \le x \le b \>» width=»» height=»» />.

Любой отрезок заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число называется Длиной числового отрезка.

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой » width=»» height=»» />.

Система сегментов обозначается _^» width=»» height=»» />. Подразумевается, что каждому натуральному числу поставлен в соответствие отрезок.

Система сегментов _^» width=»» height=»» /> называется Стягивающейся, если

• каждый следующий отрезок содержится в предыдущем; , b_] \subseteq » width=»» height=»» /> соответствующая последовательность длин отрезков бесконечно мала. (b_n — a_n) = 0″ width=»» height=»» />

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

_^ ~ \exists! c \in \R ~ \forall n \in N \colon c \in » width=»» height=»» />

_^ ~ \exists! c \in \R ~ \forall n \in N \colon c \in » width=»» height=»» />

Расстояние между концами отрезка называют его длиной и обозначают как.

27.08.2020 19:10:49

2020-08-27 19:10:49

Расчет электрических цепей

Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.

 

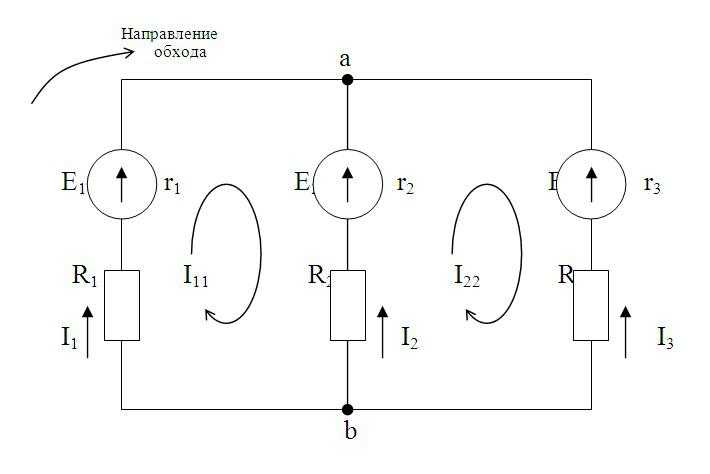
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:

Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов

Взаимное расположение прямой и точки.

Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.

Точки принято обозначать большими латинскими буквами, например, точки А
и F
. В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a
и d
.

Возможны два варианта взаимного расположения прямой и точки на плоскости
: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).

Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А
лежит на прямой а
, то можно записать . Если точка А
не принадлежит прямой а
, то записывают .

Справедливо следующее утверждение: через любые две точки проходит единственная прямая.

Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А
и В
), можно обозначать двумя этими буквами (в нашем случае прямая АВ
или ВА
).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой
или просто отрезком
. Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А
и В
являются концами отрезка, тогда этот отрезок можно обозначить АВ
или ВА

Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая»

Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ
принадлежит прямой а
, можно кратко записать .

Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А
, В
и С
лежат на одной прямой, причем точка В
лежит между точками А
и С
. Тогда можно говорить, что точки А
и С
находятся по разные стороны от точки В
. Также можно сказать, что точки В
и С
лежат по одну сторону то точки А
, а точки А
и В
лежат по одну сторону от точки С
.

Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча
. Для этого случая дается аксиома: произвольная точка О
, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О
, а две любые точки разных лучей – по разные стороны от точки О
.

Определение ломаной фигуры

Ломаная фигура — это геометрическая фигура, состоящая из набора отрезков, которые соединены в вершинах. Также ломаная фигура может быть представлена в виде замкнутой контура, при этом последняя вершина соединяется с первой.

Ломаные фигуры широко применяются в различных областях, например, в строительстве для построения планов зданий или дорог, в математике при решении задач на геометрию, в дизайне для создания графических элементов и т.д.

Ломаную фигуру можно построить с помощью координатной сетки. Для этого необходимо задать координаты каждой вершины фигуры и соединить отрезками. Также можно построить ломаную фигуру с помощью инструментов на графическом редакторе.

• Простые ломаные — фигура, в которой все линии соединяются и не пересекаются
• Замкнутые ломаные — фигура, имеющая замкнутый контур. Последняя точка соединена с первой точкой.
• Сложные ломаные — состоят из нескольких фрагментов и могут быть как замкнутыми, так и открытыми.

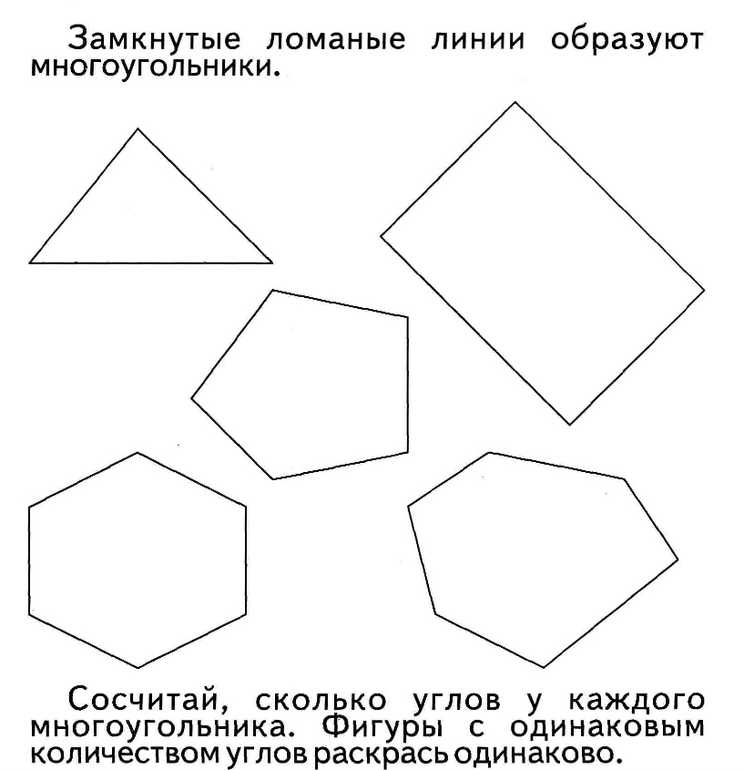
Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

треугольникомчетырехугольникапятиугольник

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

1. Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
2. Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
3. Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
4. Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
5. Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
6. Если все стороны и углы многоугольника равны, он называется правильным.

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

1. Равносторонние — все стороны их равны по длине.
2. Разносторонние — все стороны различаются по длине.
3. Равнобедренные — две стороны из трех имеют одинаковую длину.
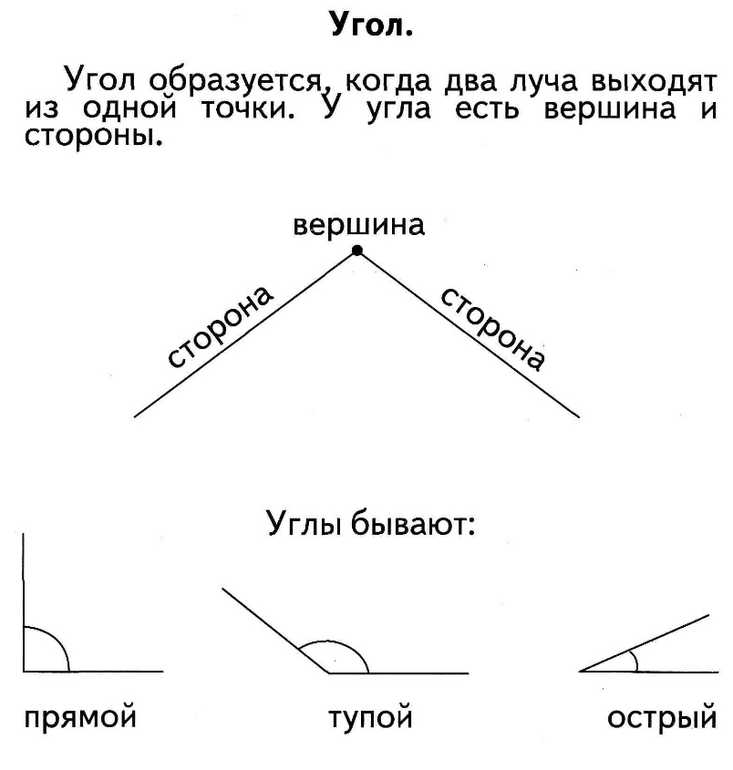
4. Остроугольные — если все углы острые.
5. Прямоугольные — если имеется прямой угол.
6. Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Урок математики во 2-м классе на тему «Длина ломаной линии»

1. Познакомить детей со способами нахождения длины ломаной. 2. Умение работать в коллективе, парах. 3. Развивать умения сравнивать и преобразовывать величины.

II. Основная часть урока

1. Повторение пройденного материала (устная работа).

а) Определение времени по часам.

Загадка

Вчера мы с вами учились определять время по часам. Давайте повторим.

Сколько минут в часе?

Сколько времени показывают часы?

18 час 15 мин.	10 часов	23 часа
20 час 15 мин	22 часа	11 часов

А сколько времени сейчас?

(В это время начался наш урок)

б) Нам надо открыть волшебную дверь, которая закрыта большим замком. К замку подберём код, в сумме должно получиться 12. Можно нажать 2,3,4 клавиши.

Мы открыли дверь и у нас в гостях “Старичок-лесовичок” со своими заданиями.

2. Изучение новой темы.

а) Преобразуйте величины.

1 дм = ….. см

5см 8 мм = ….. мм

1 см = ….. мм

72 м = ….. см ….. мм

1 м = …. см

1 дм 7 см = ….. см

1 м = ….. дм

81 см = …… дм …… см

3 м = …… дм

50 дм = …… м

5 см = …… мм

10 мм = …… см

Прочитайте тему нашего урока (Длина ломаной линии).

Найдите ломаные линии.

Чем отличается ломаная линия под № 1 от ломаной линии под № 5?

Ребята, из чего состоит ломаная линия? (Из звеньев).

Сколько в 1-ой ломаной линии звеньев, вершин?

Сколько в 5-ой ломаной линии звеньев, вершин?

А что такое ломаная линия? (Высказывания детей).

Ломаная линия – линия, которая состоит из отрезков, не лежащих на одной прямой.

Ломаная линия в математике (по С.И. Ожегову) – линия из соединяющихся под углом отрезков прямых линий.

б) Практическая работа.

Что такое ломаная линия мы повторили. Повторим, что у ломаной линии есть звенья и вершины. Лесовичок даёт нам задание. Помогите ёжику. Ёжик нашёл большие грибы, ноша тяжела. Ему надо добраться быстрее до своего домика, где его ждут ежата. Но он не знает, какая дорога короче. Как быть?

Но вот беда у нас нет линейки, а есть только 2 клубка цветных ниток. Что нам делать ? Измеряем путём наложения и сравниваем нитки.

в) Работа в парах.

Измеряем ниткой ломаную линию (Рисунок ломаной линии на каждой парте).

Удобный способ? (Нет)

Почему? (Ответ детей)

г) Лесовичок даёт нам следующее задание. У вас на парте 4 полоски. Сложите и склейте ломаную линию (жёлтая 4 см, красная 6 см, зелёная 5см, синяя 5 см).

Как другим способом измерить ломаную линию? (Измерить каждое звено)

Чему равна жёлтая, красная, зелёная, синяя?

А как узнать длину ломаной линии? (Ответы детей)

д) Работа в тетрадях.

Лесовичок даёт нам задание. Начертите ломаную линию из трёх звеньев.

Как найдём длину ломаной линии?

Ф и з м и н у т к а

е) Работа с циркулем.

Ребята, перед вами лежит лист с изображением ломаной линии (листки на каждого ребёнка).

Лесовичок предлагает нам измерить ломаную линию ни линейкой, ни ниткой, а инструментом. А как он называется, мы узнаем, отгадав загадку.

Загадка:

Сговорились две ноги Делать дуги и круги.

(Циркули раздаём на каждую парту).

Ребята, а как измерить длину ломаной линии циркулем? (Ответы детей)

Чему равна длина ломаной линии? (12 см = 2 + 7 + 3)

ж) Работа по учебнику.

1. Измерение дорожки

Лесовичок просит помочь мальчику измерить дорожку. От колодца до домика (3 + 3 = 6 см). От домика до беседки (2 + 4 = 6 см). Что можно сказать об их длине? Как узнать длину всей дорожки от колодца до беседки?

(3 + 3 + 2 + 4 = 12 см)

2. Измерение ломаной линии

I в. измеряет длину синей ломаной линии (2 + 3 + 2 = 7)

II в. измеряет длину красной ломаной линии (2 + 2 + 3 = 7 см)

– Что можно сказать о длинах ломаных линий?

– Чем отличаются ломаные линии? (Ответы детей. Одна замкнутая, а другая не замкнутая)

– Как измерить длину ломаной линии?

Вывод: (Ответы детей)

3. Повторение пройденного материала.

а) Решение задачи.

За день мимо станции прошло 3 скорых поезда и 7 товарных. Только 2 поезда на этой станции остановилось. Сколько поездов прошло мимо станции?

Источник

Основные понятия и суть обозначения ломаной

Ломаная — это геометрическая фигура, состоящая из упорядоченного набора отрезков, соединяющих последовательные точки на плоскости. В математике ломаную также называют многоугольником без самопересечений.

Основные понятия ломаной:

• Вершина: это точка, в которой ломаная изменяет направление.
• Отрезок: это отрезок прямой, соединяющий две последовательные точки ломаной.
• Сторона: это отрезок между двумя вершинами.
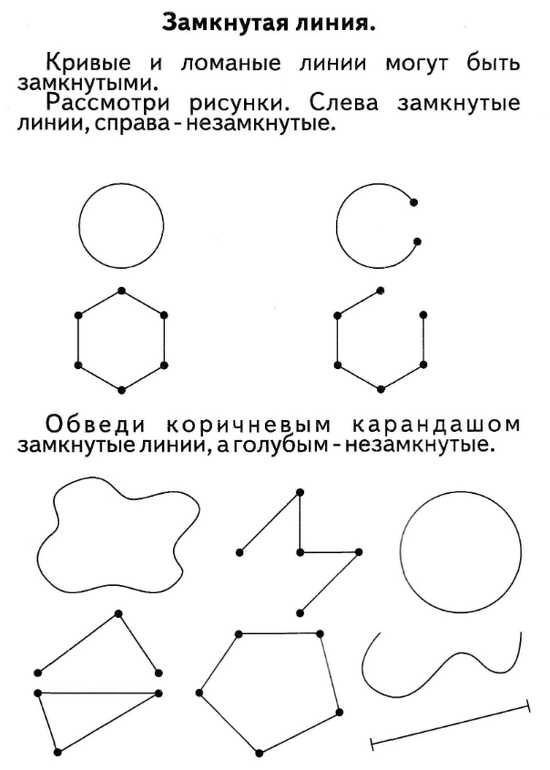
• Замкнутая ломаная: это ломаная, у которой первая и последняя точки соединены, образуя замкнутую фигуру.
• Открытая ломаная: это ломаная, у которой первая и последняя точки не соединены.

Суть обозначения ломаной заключается в том, чтобы показать последовательность точек и их соединения с помощью отрезков. Ломаная может быть представлена графически или в виде упорядоченного списка точек. Например, ломаная с вершинами A, B, C и D может быть обозначена как ABCD.

Ломаная может быть использована для представления различных объектов и явлений в разных областях науки и техники. Например, в географии ломаная может представлять линию берега или границу страны, а в программировании ломаная может быть использована для представления движения объекта на экране.

Линии — геометрия и искусство

Кандинский систематизировал свои взгляды на живопись в книге «Точка и линия на плоскости» (1926). Изучая геометрические формы, художник нашёл, что с их помощью можно усиливать или ослаблять свойства цвета. Для  этой картины он использовал приглушённую палитру, смещённую к цветам, расположенным в одной части спектра.

Цитаты из книги: ЛИНИЯГеометрическая линия – это невидимый объект. Она – след перемещающейся точки, то есть ее произведение. Она возникла из движения – а именно вследствие уничтожения высшего, замкнутого в себе покоя точки. Здесь произошел скачок из статики в динамику.Таким образом, линия – величайшая противоположность живописного первоэлемента – точки. И она с предельной точностью может быть обозначена как вторичный элемент.ВОЗНИКНОВЕНИЕСилы, приходящие извне, преобразовавшие точку в линию, могут быть различными. Разнообразие линий зависит от числа этих сил и их комбинаций.В конце концов всех форм линий можно свести к двум случаям:1. приложение одной силы и2. приложение двух сил:а) одно- или многократное поочередное воздействие обеих сил,б) одновременное воздействие обеих сил.ПРЯМАЯЕсли одна приходящая извне сила перемещает точку в каком-либо направлении, то возникает первый тип линии, причем выбранное направление остается неизменным, и сама линия стремится двигаться по прямому пути бесконечно.Это – прямая, представляющая в своем напряжении самую сжатую форму бесконечной возможности движения….Среди прямых мы выделяем три типа, по отношению к которым все прочие прямые – лишь отклонения.1. Простейшая форма прямой – это горизонталь. В человеческом представлении она соответствует линии или поверхности, на которой человек стоит или передвигается. Итак, горизонталь – это холодная несущая основа, которая может быть продолжена на плоскости в различных направлениях. Холод и плоскостность – это основные звучания данной линии, она может быть определена как кратчайшая форма неограниченной холодной возможности движения.2. Полностью противоположна этой линии и внешне, и внутренне стоящая к ней под прямым углом вертикаль, в которой плоскостность заменяется высотой, то есть холод – теплом. Таким образом, вертикаль является кратчайшей формой неограниченной теплой возможности движения.3. Третий типичный вид прямой – это диагональ, которая схематичным образом под равным углом отклоняется от обеих вышеназванных и тем самым имеет к обеим равное тяготение, что и определяет ее внутреннее звучание, равномерное соединение холода и тепла. Итак: кратчайшая форма неограниченной тепло-холодной возможности движения…

Отличие световых лучей от геометрических

В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света
. Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.

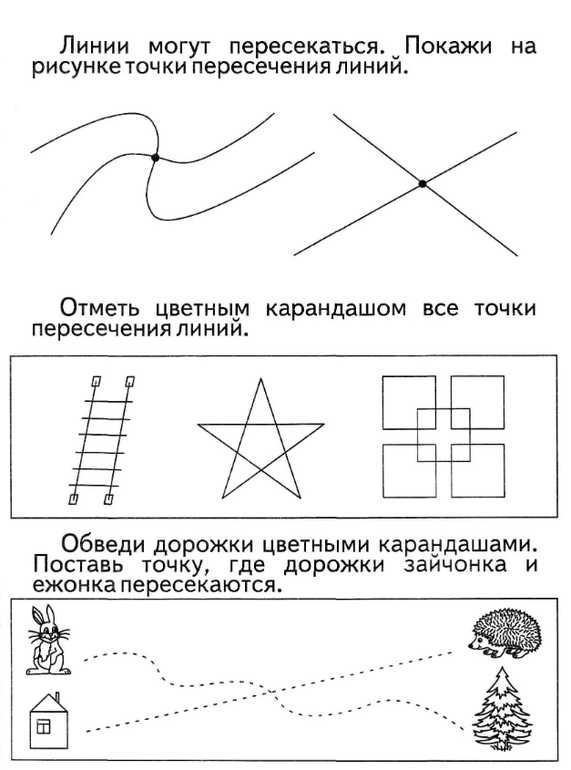
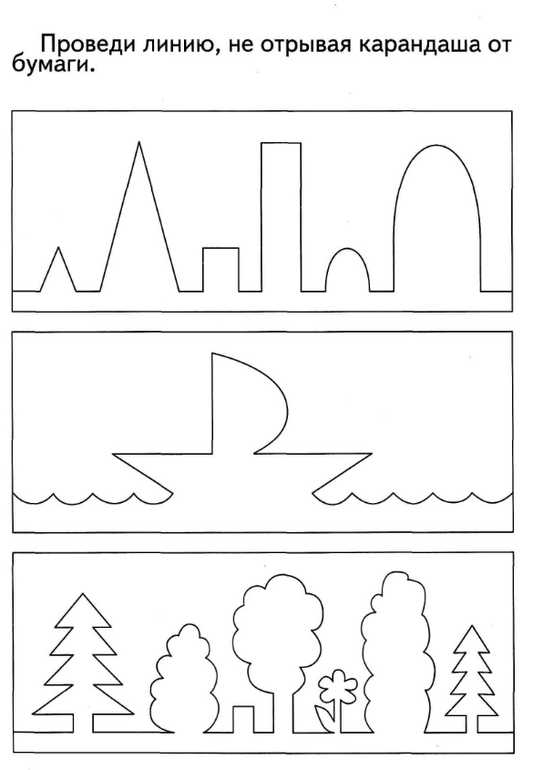
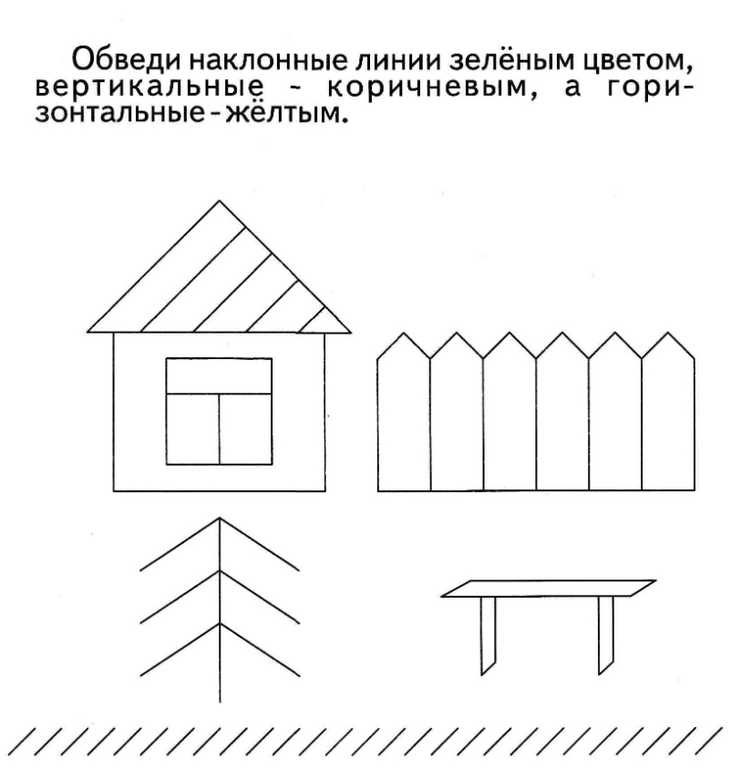
Посещая дополнительные занятия мы поняли, что не умеем оперировать понятиями точка, линия, угол, луч, отрезок, прямая, кривая, замкнутая линии и рисовать их, точнее рисовать можем, но идентифицировать не получается.

Дети должны различать линии, кривые, окружности. Это развивает у них графику и чувство правильности при занятиях рисованием, аппликацией

Важно знать, какие основные геометрические фигуры существую, что из себя представляют. Разложите карточки перед ребенком, попросите нарисовать точно так же как на картинке

Повторите несколько раз.

На занятиях нам выдали следующие материалы:

Небольшая сказка.

В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.)

Посмотрите, какие это были линии. (Прямые и кривые.)

Прямые линии похожи на натянутые веревочки, а веревочки, которые не натянули, — это кривые линии.

Сколько прямых линий? (2.)

Сколько кривых? (3.)

Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»

Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.

Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.

Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.

И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.

Вот так маленькая точка смогла изменить жизнь больших линий.

Так кто догадался кто вместе с котиком пришел к нам в гости?(прямая линия, луч, отрезок и точка)

Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.

Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)

О каких линиях вы узнали? (О прямой, луче, отрезке.)

Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)

(Берем две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)

Что узнали о луче? (У него есть начало, но нет конца.) (Педагог берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)

Что узнали об отрезке? (Унего есть и начало, и конец.) (Педагог отрезает другой конец нитки и показывает, что нитка не тянется. У нее есть и начало, и конец.)

Как начертить прямую линию? (Провести по линейке линию.)

Как начертить отрезок? (Поставить две точки и соединить их.)

И конечно прописи:

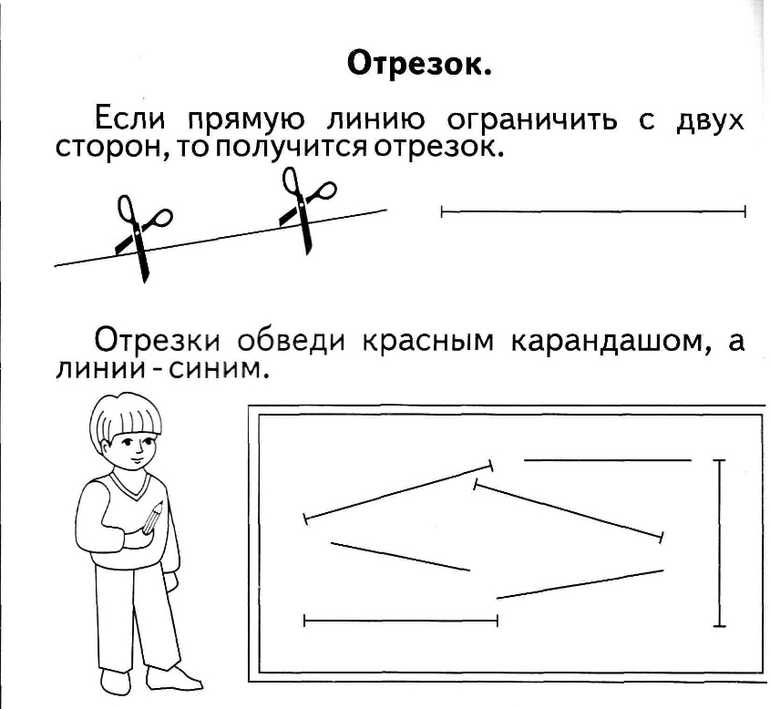
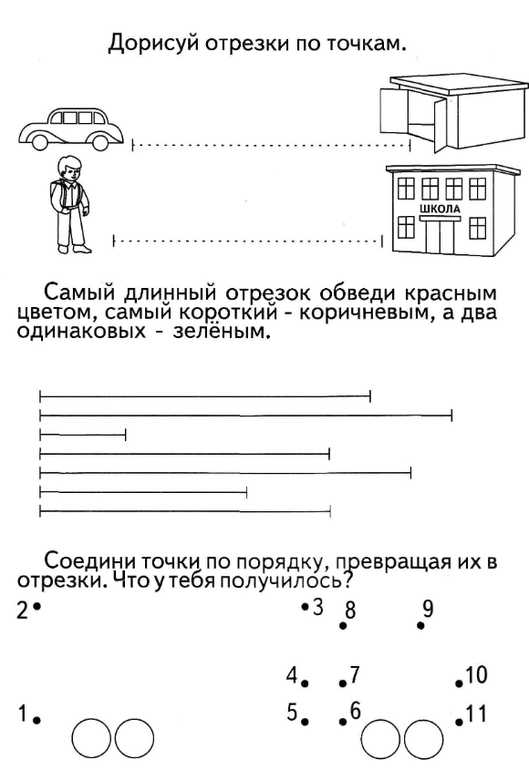
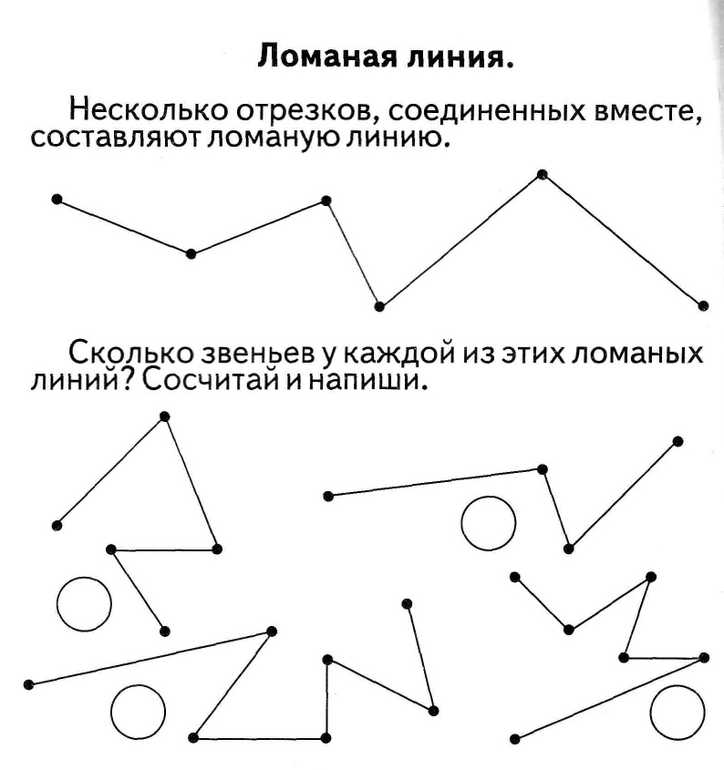
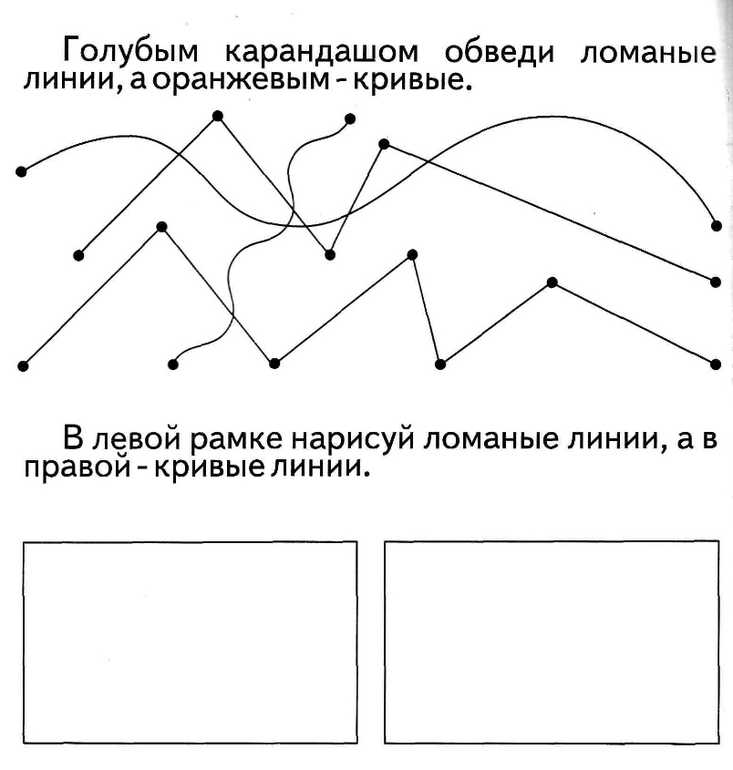
Прямая линия —
одно из фундаментальных понятий геометрии.

Наглядно прямую линию
может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.

Прямой линии
присущи такие характерные особенности
:

1.У прямой линии
нет ни начала ни конца, то есть она бесконечна.

Существует возможность начертить только ее часть.

2.Через две произвольные точки
можно провести прямую линию
, и притом только одну.

3.

Через произвольную точку
можно провести не ограниченное количество прямых на плоскости .

4.Две несовпадающие прямые на плоскости
или пересекаются в единственной точке, или они параллельны
.

Для обозначения прямой линии
используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.

Если на прямой линии указать точку
, то в результате получим два луча
:

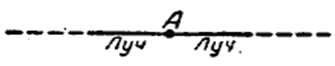
Лучом
называют часть прямой линии
, ограниченную с одной стороны. Для обозначения луча применяют или одну малую букву латинского алфавита, или две большие буквы, из которых одна обозначается в начале луча.

Часть прямой, ограниченная с обеих сторон, именуют ее отрезком
. Отрезок, как и прямая линия
, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.

Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной
. Когда концы ломаной совпадают, то такая ломаная
именуется замкнутой
.

Краткое описание

Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.

Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.

В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.

Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.

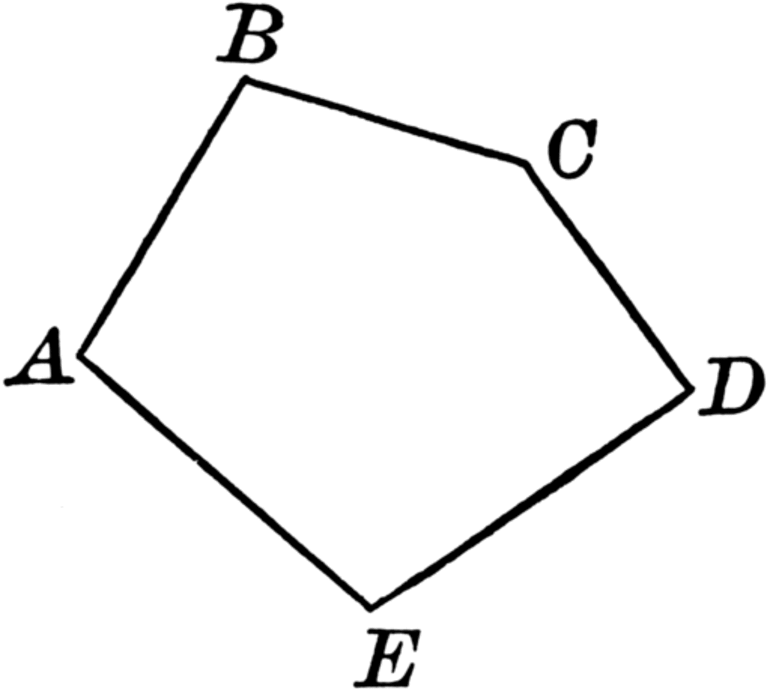
Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.

Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.

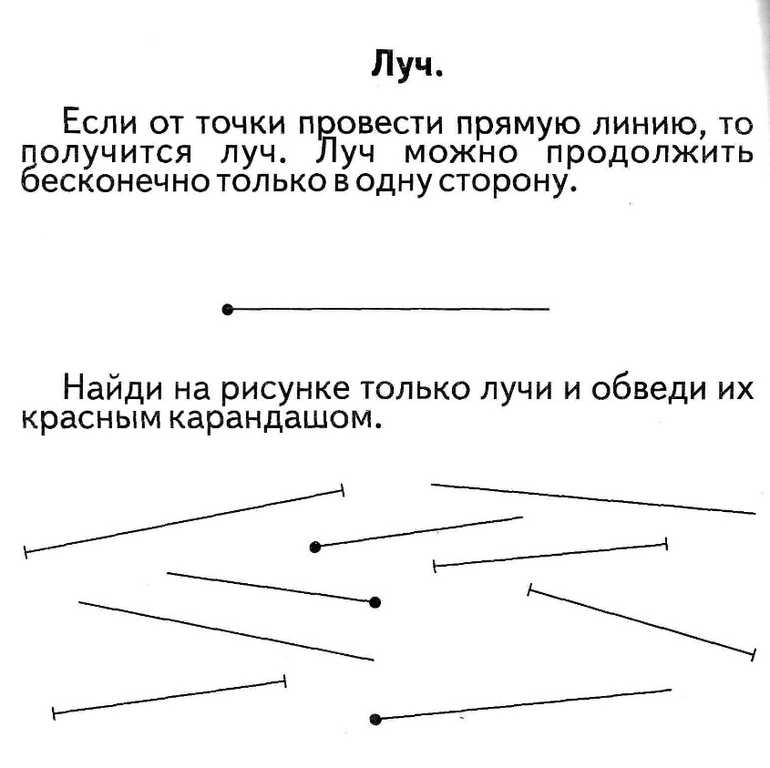
Что такое луч в математике

Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.

Луч — геометрическое понятие

Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.

На картинке вы можете посмотреть, что такое луч и как он выглядит:

Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.

Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.

Отличия луча от прямой и от отрезка

В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.

В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.

В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.

Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:

• отрезок имеет начальную и конечную точки;
• луч — только начало;
• прямая — не располагает начальной и конечной точками.

Взаимное расположение лучей

Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.

На рисунке начало для лучей — общая точка A.

По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.

Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.

Дополнительные лучи — это фигуры, которые обладают такими признаками, как:

• имеют совпадающее начало в одной точке;
• располагаются на одной прямой линии;
• направляются в разные стороны, то есть угол между ними составляет 180 градусов.

Можно ли сравнить два луча?

Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.

Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.

Луч — альтернативные значения слова

Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.

Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.

Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:

• Солнце;
• звёзды;
• лампочка.

В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.

Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.

Разновидности

В геометрии принято различать несколько разновидностей по структуре:

1. Замкнутые самопересекающиеся.
2. Незамкнутые самопересекающиеся.
3. Замкнутые без самопересечений.
4. Незамкнутые без самопересечений.

Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.

Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником
. Ломаная из четырех звеньев получила название четырехугольника
. Фигура из пяти отрезков — пятиугольник
и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником
. Другое ее название — многоугольная область
.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

1. Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
2. Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
3. Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
4. Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
5. Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
6. Если все стороны и углы многоугольника равны, он называется правильным.

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

1. Равносторонние — все стороны их равны по длине.
2. Разносторонние — все стороны различаются по длине.
3. Равнобедренные — две стороны из трех имеют одинаковую длину.
4. Остроугольные — если все углы острые.
5. Прямоугольные — если имеется прямой угол.
6. Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Примеры использования ломаных линий

В изобразительном искусстве: ломаные линии используются в художественных произведениях для передачи форм и контуров объектов. Они могут быть использованы для создания эффекта перспективы или движения.

В географических картах: ломаные линии используются для обозначения границ государств, рек, дорог и других географических объектов. Они могут быть использованы для передачи информации об уровне высот и наклона местности.

В экономике: ломаные линии могут быть использованы для графического представления изменений цен, продаж, прибыли и других показателей экономической деятельности.

В научных исследованиях: ломаные линии используются для представления результатов исследований, например, изменения температуры или концентрации вещества.

В архитектуре и дизайне: ломаные линии могут быть использованы для создания оригинальных и необычных форм и объектов, таких как мебель, здания, структуры и прочее.

Какие типы ломаных существуют и какими свойствами они обладают?

В математике существует несколько типов ломаных, каждая из которых имеет свои особенности и свойства:

• Простая ломаная — состоит из отрезков, которые не пересекаются и не имеют общей точки, кроме смежных концов. Простая ломаная может быть замкнутой или незамкнутой.

• Система ломаных — состоит из нескольких простых ломаных, которые могут быть как замкнутыми, так и незамкнутыми. В системе ломаных каждая ломаная может быть соединена с другой общим концом.

• Несамопересекающаяся ломаная — каждый отрезок такой ломаной не пересекает себя, а также все вершины лежат на одной прямой.

• Самопересекающаяся ломаная — содержит отрезки, которые могут пересекать друг друга, а также вершины лежат не на одной прямой.

• Многоугольник — разновидность ломаной, образованной замкнутой системой отрезков без самопересечений. Многоугольник имеет определенную площадь и периметр.

Это лишь некоторые из типов ломаных, с которыми можно столкнуться в математике. Каждый тип имеет свои уникальные свойства, которые определяются их структурой и определением.