Признаки равенства прямоугольных треугольников

Введение и доказательство четвёртого признака равенства прямоугольных треугольников, введение понятия «внешний угол треугольника»

Рас­смот­рим сле­ду­ю­щий при­знак ра­вен­ства тре­уголь­ни­ков:

Если катет и ги­по­те­ну­за од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны ка­те­ту и ги­по­те­ну­зе дру­го­го тре­уголь­ни­ка, такие пря­мо­уголь­ные тре­уголь­ни­ки равны.

Рис. 7

До­ка­за­тель­ство:

Сов­ме­стим на­ло­же­ни­ем тре­уголь­ни­ки АВС и А1В1С1. Пред­по­ло­жим, что вер­ши­ны А и А1, а также С и С1 сов­ме­сти­лись на­ло­же­ни­ем, а вер­ши­на В и точка В1 не сов­па­да­ют. Имен­но этот слу­чай ука­зан на сле­ду­ю­щем ри­сун­ке:

Рис. 8

В дан­ном слу­чае мы можем за­ме­тить рав­но­бед­рен­ный тре­уголь­ник АВВ1 (по опре­де­ле­нию – по усло­вию АВ = АВ1). По­это­му по свой­ству, ∠АВ1В = ∠АВВ1. Рас­смот­рим опре­де­ле­ние внеш­не­го угла. Внеш­ним углом тре­уголь­ни­ка на­зы­ва­ет­ся угол, смеж­ный лю­бо­му углу тре­уголь­ни­ка. Его гра­дус­ная мера равна сумме двух углов тре­уголь­ни­ка, несмеж­ных с ним. На ри­сун­ке ука­за­но дан­ное со­от­но­ше­ние:

Рис. 9

Угол 5 яв­ля­ет­ся внеш­ним углом тре­уголь­ни­ка и равен ∠5 = ∠1 + ∠2. От­сю­да сле­ду­ет, что внеш­ний угол боль­ше каж­до­го из углов, несмеж­ных с ним.

Таким об­ра­зом, ∠АВВ1 яв­ля­ет­ся внеш­ним углом для тре­уголь­ни­ка АВС и равен сумме ∠АВВ1  = ∠САВ + ∠АСВ = ∠АВС  = ∠САВ + 90о. Таким об­ра­зом, ∠АВ1В (что яв­ля­ет­ся ост­рым углом в пря­мо­уголь­ном тре­уголь­ни­ке АВВ1) не может быть равен углу ∠АВВ1, ведь дан­ный угол – тупой по до­ка­зан­но­му.

Зна­чит наше пред­по­ло­же­ние ка­са­тель­но рас­по­ло­же­ния точек В и В1 ока­за­лось невер­ным, сле­до­ва­тель­но дан­ные точки сов­па­да­ют. А зна­чит тре­уголь­ни­ки АВС и А1В1С1 сов­ме­сти­лись на­ло­же­ни­ем. По­это­му они равны (по опре­де­ле­нию).

Таким об­ра­зом, дан­ные при­зна­ки вво­дят­ся не зря, ведь их можно ис­поль­зо­вать при ре­ше­нии неко­то­рых задач.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/7-klass/sootnosheniya-mezhdu-storonami-i-uglami-treugolnikov/priznaki-ravenstva-pryamougolnyh-treugolnikov-2

https://www.youtube.com/watch?v=bnj64AX-XpI

http://idata.5gbfree.com/data/img/detskie/repetitor/geometriay/1020.jpg

http://u.900igr.net/zip/ee26a03498d564d73d320649486eb080.zip

http://gdz-matem.ru/228-priznaki-ravenstva-pryamougolnyh-treugolnikov.html

Содержание

• Слайд 1

  Признаки равенства треугольников

  Треугольник и его элементы
  Задачи по теме «Первый признак равенства треугольников»
  Задачи по теме «Второй признак равенства треугольников»
  Задачи по теме «Третий признак равенства треугольников»
  Справочный материал (формулировка теоремы и ее доказательство):
  а) Первый признак равенства треугольников
  б) Второй признак равенства треугольников
  в) Третий признак равенства треугольников

  pptcloud.ru

• Слайд 2

  D
  N
  L

  Назовите:
  1) сторону, лежащую против угла N :
  2) сторону, лежащую против угла NDL:
  3) угол, лежащий против стороны DN:
  4) угол, лежащий против стороны DL:
  5) углы, прилежащие к стороне NL: и

  Треугольник

  Рис. 1

• Слайд 3

  Первый признак равенства треугольников

  M
  F
  N
  L
  O

  Докажите, что OLF = OMN

  Решение:
  1) Рассмотрим OLF и :
  а) OL =- по условию,
  б) OF =- по условию,

  Задача. Заполните пропуски.
  Следовательно OLF = — по двум сторонам и углу между ними.
  Рис. 2
  в) LOF = — каквертикальные углы.

• Слайд 4

  B
  S
  A
  R
  Задача. Заполните пропуски.
  S

  Докажите, что ARS = BRS

  а) Сторона = — по условию.
  б) Сторона = — общая сторона.
  в) = — по условию.
  г) Следовательно, ARS = — по двум
  и углу .
  2) Т. к. ASR= BSR, то соответственные стороны и углы равны, BR = AR = 18 см, BRS = ARS =

  15˚

  Решение:

  1) Рассмотрим ARS и

  Рис. 3

• Слайд 5

  Второй признак равенства треугольников
  Задача.
  Докажите, что AXO = BZO

  Решение:

  A
  X
  B
  Z
  O

  1) Рассмотрим BZO и
  У них: а) Сторона = — по условию;
  б) = — по условию;
  в) = — как вертикальные.
  Следовательно AXO = — по стороне и двум прилежащим к ней .

  Рис. 4

• Слайд 6

  Задача.

  F
  B
  D
  A

  На рисунке 5 луч DF биссектриса угла ADF
  а) Докажите, что ADF = BDF;
  б) Найдите сторону BD и DBF.
  Решение:
  а) Рассмотрим ADF и .
  У них: 1) = — общая сторона;
  2) = — по условию;
  3) = , так как DF –
  17 дм

  110˚

  биссектриса ADB.
  Следовательно, ADF = поиприлежащим к ней.
  б) Из равенства треугольников следует равенство соответствующих сторон и углов,то есть сторона DB == дм, B = =.

  ˚
  Рис. 5

• Слайд 7

  Третий признак равенства треугольников

  A
  N
  B
  C

  108̊
  а) Докажите, что CAN = BAN
  б) Найдите ABN.

  Решение:
  а) Рассмотрими BAN.
  У них: 1) AC = — по условию;
  2) CN = — по условию;
  3) AN = AN – общая сторона.
  Значит, CAN = — по трем .
  б) Из равенства треугольников CAN и BAN следует равенство соответствующих углов, то естьABN = = .
  Рис. 6

  ˚

• Слайд 8

  Рассмотрим треугольники ABC и DEF, у которых AB=DE, AC=DF, углы A и D равны (рис. 7). Докажем, что ABC= DEF.
  Так как A=D, то треугольник ABC можно наложить на треугольник DEF так, что вершина A совместится с вершиной D, а стороны AB и AC наложатся соответственно на лучи DE и DF. Поскольку AB=DE, AC=DF, то сторона AB совместится со стороной DE, а сторона AC – со стороной DF; в частности, совместятся точки B и E, C и F. Следовательно, совместятся стороны BC и EF. Итак, треугольники ABC и DEF полностью совместятся, значит, они равны.

  Рис. 7
  C
  A
  B
  D
  E
  F

  Теорема

  Доказательство

  Теорема доказана.

• Слайд 9

  Теорема
  Рассмотрим треугольники ABC и DEF, у которых AB=DE, A= D, B= E (рис. 8). Докажем, что ABC= DEF.
  Наложим треугольник ABC на треугольник DEF так, чтобы вершина A совместилась с вершиной D, сторона AB – с равной ей стороной DE, а вершины C и F оказались по одну сторону от прямой DE.
  Так как A=D и B= E, то сторона AC наложится на луч DF, а сторона BC – на луч EF. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче DF, так и на луче EF и, следовательно, совместится с общей точкой этих лучей – вершиной F. Значит, совместятся стороны AC и DF, BC и EF.
  Итак, треугольники ABC и DEF полностью совместятся, поэтому они равны.
  Теорема доказана.

  C
  A

  B

  Рис. 8
  D
  E
  F

  Доказательство

• Слайд 10

  Теорема
  Доказательство
  Рассмотрим треугольники ABC и DEF, у которых AB = DE, BC = EF, CA = FD (рис. 9). Докажем, что ABC = DEF. Приложим треугольник ABC к треугольнику DEF так, чтобы вершина A совместилась с вершиной D, вершина B – с вершиной E, а вершины C и F оказались по разные стороны от прямой DE (рис. 10).
  Возможны три случая: луч FC проходит внутри угла DFE (рис. 10, а); луч FC совпадает с одной из сторон этого угла (рис. 10, б); луч FC проходит вне угла DFE (рис. 10, в). Рассмотрим первый случай (остальные случаи можете рассмотреть самостоятельно).
  Так как по условию теоремы стороны AC и DF, BC и EF равны, то треугольники DFC и EFC – равнобедренные (см. рис. 10, а). По теореме о свойстве углов равнобедренного треугольника 1 = 2, 3 = 4, поэтому DCE = DFE. Итак, AC = DF, BC = EF,C = F.
  Следовательно, треугольники ABC и DEF равны по первому признаку равенства треугольников.
  Теорема доказана.

  Рис. 9

  A
  C
  B

  F
  D
  E

  D (A)
  C
  F
  E (B)

  D (A)
  E (B)
  C
  F
  Рис. 10
  а)
  б)

  в)

  E (B)
  C
  F
  D (A)

  1

  3

  2
  4

Посмотреть все слайды

Особенности многоугольников с тремя углами

Признаком прямоугольного треугольника является прямой угол. Образуют его стороны — катеты. Равными называются фигуры, которые можно совместить наложением друг на друга. Другими словами, соответствующие стороны двух и более треугольников имеют одинаковую длину. Для определения признаков равенства прямоугольных многоугольников используют особенности фигур. Заключаются они в следующем:

1. Если сложить 2 угла, отличные от прямого, их сумма составит 90 градусов. Например, α = y + β = 90.
2. Синус прямого угла в прямоугольном многоугольнике можно найти как отношение противолежащего катета к гипотенузе: sin (α) = BC / AB; sin (β) = AC / AB.
3. Косинус острого угла в фигуре можно найти, разделив прилежащий катет на гипотенузу: sin (α) = A C / AB; sin (β) = B C / AB.
4. Если в треугольнике стороны, образующие прямой угол, одинаковые по длине, сумма их квадратов равняется произведению гипотенузы самой на себя. Это правило называется теоремой Пифагора и в математическом виде записывается так: c = √‎ (a2 + b2).
5. Пусть n и m проекции катетов на гипотенузу. Тогда будут справедливы следующие равенства: a 2 = n * c, b2 = m * c.
6. Высоты, построенные из вершин прямых углов, равны среднему геометрическому проекций катетов на гипотенузу. Кроме этого, высота, опущенная из вершины прямого угла на гипотенузу, делит её в таком отношении, в каком находятся квадраты прилежащих катетов.
7. Медианы пересекаются в одной точке, находящейся внутри фигуры и делятся в ней 2 к 1, если вести отсчёт от вершины. Это место является центром тяжести фигуры.
8. Биссектрисы острых углов в точке пересечения образуют угол равный 45 градусам.
9. Определить длину медианы, проведённой к катетам, можно, зная размер проекций, опущенных на них: m2a = b2 — a2 / 4; m2b = a2 — b2 / 4.
10. Найти длину биссектрисы можно, воспользовавшись выражением: L = √‎2 * (a * b) / (a + b).
11. Площадь прямоугольного треугольника равняется сумме двух катетов, разделённой на 2 или пропорциональна произведению гипотенузы на высоту и обратно пропорциональна 2: S = (a * b) / 2 = (h * c) / 2.

Пример задачи

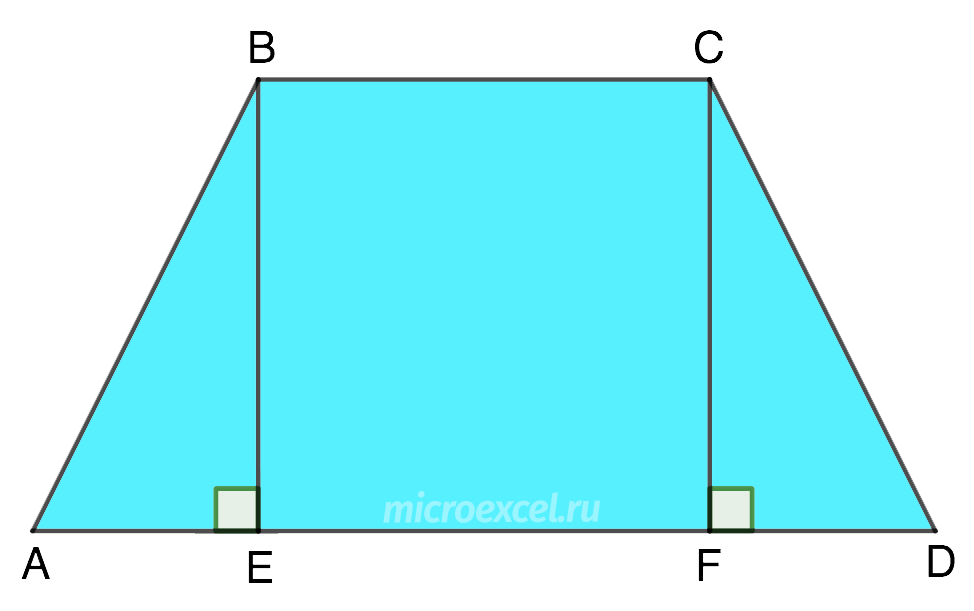
Дана трапеция ABCD, в которой на основание AD опущены две высоты – BE и CF. При этом отрезки AE и FD равны. Докажите, что трапеция ABCD – равнобокая.

Решение

Трапеция ABCD является равнобокой, если равны AB и CD.

Опущенные на основание AD высоты образуют два прямоугольных треугольника – △ABE и △FCD.

По условиям задачи AE и FD, которые являются катетами рассматриваемых треугольников, равны.

BE и CF – это высоты трапеции, одновременно являющиеся катетами наших треугольников. Как расстояния между двумя параллельными линиями (основаниями трапеции), они также имеют одинаковую длину.

Таким образом, мы имеем два прямоугольных треугольника c равными катетами (AE=FD и BE=CF). Это является одним из признаков равенства фигур.

Это значит, что AB=CD (гипотенузы треугольников). Отсюда следует, что трапеция ABCD – равнобокая.

Признак равенства прямоугольных треугольников по двум катетам

Рассмотрим два прямоугольных треугольника $\bigtriangleup{ABC}$ и $\bigtriangleup{A_{1}B_{1}C_1}$, у которых соответственно равны катеты $AB=A_{1}B_1$ и $AC=A_{1}C_1$. Видим, что в таком случае треугольники равны согласно первому признаку равенства:

$$AB=A_{1}B_1\\AC=A_{1}C_1\\\angle{A}=\angle{A_1}~(\textcolor{purple}{90^\circ})$$

Сформулировать первый признак равенства применительно к прямоугольным треугольникам, следовательно, можно не по двум сторонам и углу между ними, а только по двум сторонам. То есть катетам.  

{"questions":,"explanations":["Верно, из первого признака равенства по «двум сторонам и углу между ними».","",""],"answer":}}}]}

Пример задачи

Дана трапеция ABCD, в которой на основание AD опущены две высоты – BE и CF. При этом отрезки AE и FD равны. Докажите, что трапеция ABCD – равнобокая.

Решение

Трапеция ABCD является равнобокой, если равны AB и CD.

Опущенные на основание AD высоты образуют два прямоугольных треугольника – △ABE и △FCD.

По условиям задачи AE и FD, которые являются катетами рассматриваемых треугольников, равны.

BE и CF – это высоты трапеции, одновременно являющиеся катетами наших треугольников. Как расстояния между двумя параллельными линиями (основаниями трапеции), они также имеют одинаковую длину.

Таким образом, мы имеем два прямоугольных треугольника c равными катетами (AE=FD и BE=CF). Это является одним из признаков равенства фигур.

Это значит, что AB=CD (гипотенузы треугольников). Отсюда следует, что трапеция ABCD – равнобокая.

Практические задания и задачи №№ 121-142

№ 121. □ Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC. а) Докажите, что ΔСВО = ΔDAO; б) найдите ВС и СО, если CD = 26 см, AD = 15 см.

№ 122. □ На рисунке 53 ∠1 = ∠2, ∠3 = ∠4. а) Докажите, что ΔАВС = ΔCDA; б) найдите АВ и ВС, если АО =19 см, CD = 11 см.

№ 123. □ На биссектрисе угла А взята точка D, а на сторонах этого угла — точки В и С такие, что ∠ADB = ∠ADC. Докажите, что BD = CD.

№ 124. □ По данным рисунка 73 докажите, что ОР = ОТ, ∠P = ∠T.

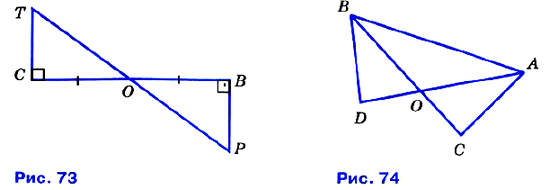
№ 125. □ На рисунке 74 ∠DAC = ∠DBC, АО = ВО. Докажите, что ∠C = ∠D и AC = BD.

№ 126. □ На рисунке 74 ∠DAB = ∠CBA, ∠CAB = ∠DBA, АС =13 см. Найдите BD.

№ 127. В треугольниках АВС и А₁В₁С₁, АВ = А₁В₁, ВС = В₁С₁, ∠B = ∠B₁. На сторонах АВ и A₁B₁, отмечены точки D и D₁ так, что ∠ACD = ∠A₁C₁D₁. Докажите, что ΔBCD = ΔB₁C₁D₁.

№ 128. Докажите, что в равных треугольниках биссектрисы, проведённые к соответственно равным сторонам, равны.

№ 129. Отрезки АС и BD пересекаются в середине О отрезка АС, ∠BCO = ∠DAO. Докажите, что ΔВОА = ΔDOC.

№ 130. В треугольниках АВС и А₁В₁С₁, отрезки СО и С₁О₁ — медианы, BC = B₁C₁, ∠B = ∠B₁ и ∠C = ∠C₁. Докажите, что: а) ΔАСО = ΔА₁С₁О₁; б) ΔВСO = ΔВ₁С₁O₁.

№ 131. В треугольниках DEF и MNP EF = NP, DF = MP и ∠F = ∠P. Биссектрисы углов Е и D пересекаются в точке О, а биссектрисы углов М и N — в точке К. Докажите, что ∠DOE = ∠MKN.

№ 132. Прямая, перпендикулярная к биссектрисе угла А, пересекает стороны угла в точках М и N. Докажите, что треугольник AMN — равнобедренный.

№ 133. Докажите, что если биссектриса треугольника является его высотой, то треугольник — равнобедренный.

№ 134. Докажите, что равнобедренные треугольники равны, если основание и прилежащий к нему угол одного треугольника соответственно равны основанию и прилежащему к нему углу другого треугольника.

№ 135. Докажите, что если сторона одного равностороннего треугольника равна стороне другого равностороннего треугольника, то треугольники равны.

№ 136. □ На рисунке 52 АВ = АС, BD = DC и ∠BAC = 50°. Найдите ∠CAD.

№ 137. На рисунке 53 BC = AD, AB = CD. Докажите, что ∠B = ∠D.

№ 138. На рисунке 75 AB = CD и BD = АС. Докажите, что: a) ∠CAD = ∠ADB; б) ∠BAC = ∠CDB.

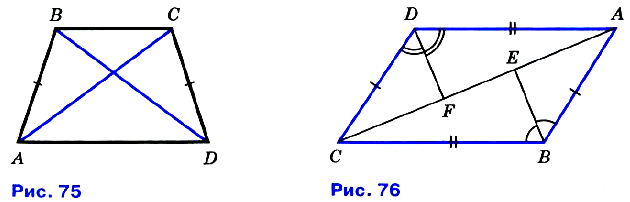
№ 139. На рисунке 76 АВ = CD, AD = BC, BE — биссектриса угла ABC, a DF — биссектриса угла ADC. Докажите, что: а) ∠ABE = ∠ADF; б) ΔАВЕ = ΔCDF.

№ 140. В треугольниках АВС и А₁В₁С₁ медианы ВМ и В₁М₁ равны, АВ = А₁В₁ и АС = А₁С₁. Докажите, что ΔАВС = ΔА₁В₁С₁.

№ 141. В треугольниках АВС и А₁В₁С₁ отрезки AD и A₁D₁ — биссектрисы, АВ = А₁В₁, BD = B₁D₁ и AD = A₁D₁. Докажите, что ΔАВС = ΔА₁В₁С₁.

№ 142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезок CD в точке О. Докажите, что: a) ∠ADB = ∠ACB; б) DO = OC.

Вы смотрели: Практические задания и задачи №№ 121-142 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: (19. Второй признак равенства треугольников.  20. Третий признак равенства треугольников). Геометрия Атанасян Задачи 121-142 + Ответы.

◄ Задачи 100-120 ОГЛАВЛЕНИЕ учебника  Задачи 143-155 ►

Построение треугольника по трём данным его сторонам. Третий признак равенства треугольников

Пусть требуется построить треугольник по трём его сторонам, например, сторона а = 30 мм, сторона с = 40 мм и сторона b = 42 мм. (Заданные размеры должны удовлетворять условию: сумма двух любых сторон треугольника больше третьей стороны.)

Сначала на произвольной прямой построим отрезок АС, равный данному отрезку b, т. е. 42 мм; мы сразу получим две вершины искомого треугольника — А и С.

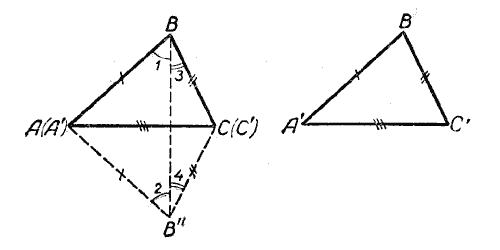
Так как длина второй и третьей сторон соответственно равна отрезкам с и а (в данном случае 40 мм и 30 мм), то третья вершина треугольника должна находиться как на дуге, описанной из центра А радиусом, равным 40 мм, так и на дуге, описанной из центра С радиусом, равным 30 мм. Следовательно, третьей вершиной треугольника будет точка пересечения этих дуг. Обозначив эту точку буквой В и соединив её отрезками с точками А и С, получим искомый треугольник ABC.

По тем же данным построим второй треугольник — Δ А’В’С’ и докажем, что Δ АВС = Δ А’В’С’. Для этого приложим треугольник А’В’С’ к треугольнику ABC так, чтобы их равные стороны А’С’ и AС совместились, причём точка А’ совпала бы с точкой А, точка С — с точкой С. Тогда треугольник А’В’С’ примет положение АВ»С. Сторона АВ будет равна стороне АВ» и сторона ВС — стороне В»С.

Соединив отрезком прямой точки В и В», получим два равнобедренных треугольника ВАВ» и ВСВ», у которых ∠1 = ∠2, а ∠3 = ∠4, откуда ∠B = ∠B». Следовательно, Δ АВС = Δ АВ»С, но тогда и Δ АВС = Δ А’В’С’.

По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.

Мы доказали, что если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой.

Назовём это третьим признаком равенства треугольников.

Замечания. 1. Во всех трёх признаках равенства треугольников в число трёх данных элементов входит хотя бы одна сторона треугольника.

2. В равных треугольниках против равных сторон лежат равные углы и, обратно, против равных углов лежат равные стороны.

Итак, три признака равенства треугольников:

Некоторые свойства прямоугольных треугольников

Свойство 1. Сумма двух острых углов прямоугольного треугольника равна 90°.

Действительно. Поскольку сумма углов треугольника равна 180°, а прямой угол равен 90°, то сумма остальных углов равен 90°.

Свойство 2. Если катет прямоугольного треугольника лежит напротив угла в 30°, то он равен половине гипотенузы.

Доказательство. Рассмотрим прямоугольный треугольник ACB, у которого угол C прямой, а угол ∠ABC=30°. Приложим к этому треугольнику равному ему прямоугольный треугольник как показано на Рис.2.

Рассмотрим треугольник ADB. Так как ∠A=∠D=∠ABD=60°, то треугольник ABD равносторонний. Следовательно AB=AD=BD. Тогда . Конец доказательства.

Свойство 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против данного катета равен 30°.

Доказательство. Пусть у прямоугольного треугольника катет AC равен половине гипотенузы AB. Аналогично вышеизложенному приложим к этому треугольнику равному ему прямоугольный треугольник BCD(Рис.2). Получим равносторонний треугольник, где AB=AD=BD. Тогда ∠A=∠D=∠ABD=60°. Но ∠ABD=2∠ABС. Следовательно . Конец доказательства.

Геометрия 7 класс задача по теме треугольники, пояснение решения задач

Решим несколько задач про треугольники:

• нахождение периметра;
• доказательство равенства треугольников.

Чтобы найти периметр в представленной задаче, нашли сперва неизвестные стороны. Потом просто сложили полученные значения.

Для этой задачи понадобилось знание признаков равенства треугольников.

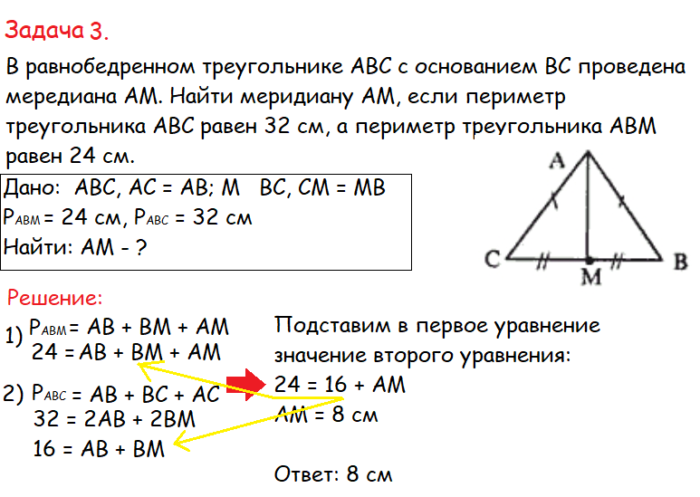Для решения задачи понадобится знание признаков равнобедренного треугольника. Так, можно утверждать, что в треугольнике сторона АС и АВ равны, как и СМ и МВ. Поскольку периметр — это сумма всех сторон, получается, что сумму периметра АВМ можно записать сложением АВ, ВМ и АМ (ее как раз нужно найти).

Сумму периметра АВС также записали с помощью сложения сторон. Затем упростили это сложение, записав: 32 = 2 АВ + 2 ВМ (так как АВ и АС равны — равнобедренный треугольник; ВМ и СМ тоже равны). Потом эту запись сократили, разделив на 2.

Вышло, что сумма двух сторон равна 16 см. Остается найти третью сторону (АМ). Она входит в треугольник АВМ, периметр которого равен 24 см. Тогда, чтобы найти третью сторону (АМ, нужно просто 24 отнять 16, вышло 8 см. В примере подставили в уравнение, чтобы не запутаться.

Решим задачу на нахождение угла в треугольнике.

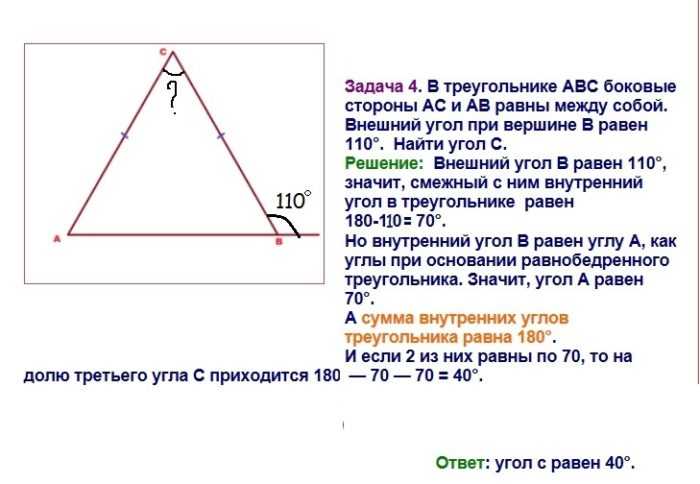
Чтобы найти угол С в задаче потребовалось узнать, чему равен угол В. По условиям известно, что внешний В равняется 110º. Знаем, что развернутый угол равняется 180º (это внешний и внутренний угол В в сумме). Поэтому от 180 отнимаем 110. Получается угол В = 70º.

Треугольник равнобедренный, значит углы при основании одинаковые ⇒ угол В = углу А = 70º.

Поскольку сумма углов треугольника равна 180º (по правилу), значит угол С = 180 — углы А и В = 180 — 70 — 70 = 40°.

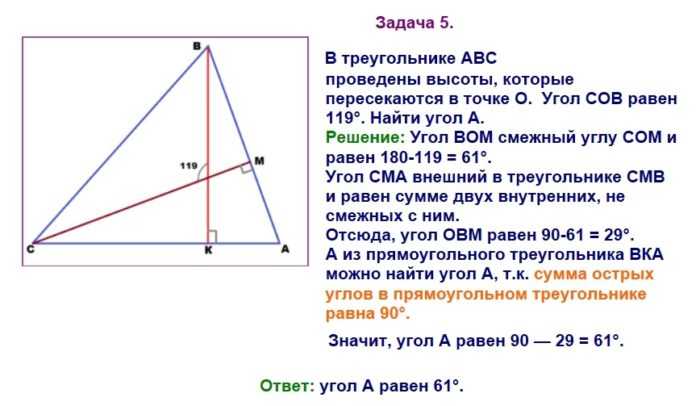Задачи на второй и третий признак равенства треугольников подробно представлено в видео-уроке.

Признаки равенства прямоугольных треугольников

Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.

1. Признак равенства по двум катетам

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны

Данный признак следует из первого признака равенства треугольников.

Пример:

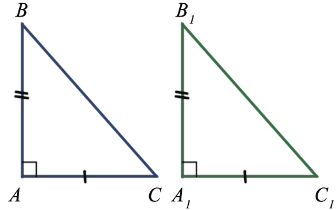
ABC
A₁B₁C₁AB = A₁B₁ACA₁C₁

2. Признак равенства по катету и острому углу

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны

Данный признак следует из второго признака равенства треугольников.

Пример:

ABC
A₁B₁C₁ACA₁C₁
C
C₁

3. Признак равенства по гипотенузе и острому углу

Теорема

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,то такие треугольники равны

Пример:

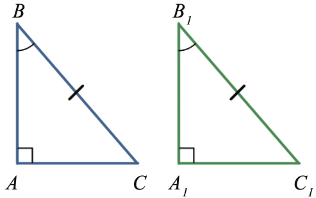
ABC
A₁B₁C₁BCB₁C₁
B
B₁

Доказательство

Так как сумма двух острых углов прямоугольного треугольника равна 90 0 , то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по стороне(по гипотенузе) и двум прилежащим к ней углам, что и требовалось доказать.

4. Признак равенства по катету и гипотенузе

Теорема

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны

Пример:

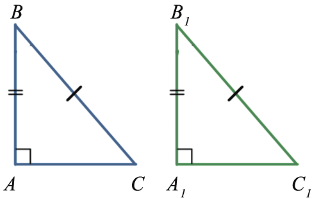
ABC
A₁B₁C₁BCB₁C₁ABA₁B₁

Доказательство

Дано:

ABC
A₁B₁C₁, BCB₁C₁ABA₁B₁

Доказать:

ABC
A₁B₁C₁

Доказательство:

Рассмотрим данные треугольники:

Так как

A
A₁
ABC
A₁B₁C₁AA₁ACAB A₁C₁A₁B₁BB₁ABA₁B₁C C₁предположитьC другой C₂ A₁C₁равнобедренныйC₁B₁C₂

В

C₁B₁C₂не равны
C₂острый
C₁тупой B₁C₁A₁равнобедренногоравныC совместитсяC₁совместятсяABCA₁B₁C₁они равнычто и требовалось доказать

Пятый признак (по катету и гипотенузе).

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

Дано:

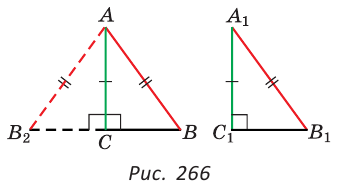
Доказать:

Доказательство:

Приложим треугольников А₁В₁С₁ к треугольнику АВС так, чтобы совместились равные катеты А₁С₁ и АС, а вершины В₁ и В лежали по разные стороны от прямой АС. Треугольник А₁В₁С₁ займет положение треугольника АВ₂С. Так как

₂₂₂₂

Отсюда

Пример:

На рисунке 267

Доказать равенство треугольников: а)

АВС и
ADC б)
АОВ и

Доказательство:

а) Рассмотрим прямоугольные треугольники ABC и ADC. У них гипотенуза АС — общая, катеты AD и ВС равны по условию. Тогда

АВС =
ADC

б) Из равенства треугольников ABC и ADC следует равенство сторон АВ и CD (доказано в пункте а). Тогда

АОВ =

Пример:

Дан треугольник ABC, АК и СМ — его высоты, проведенные к боковым сторонам, О — точка их пересечения (рис. 268). Доказать, что если треугольники АОМ и СОК равны, то треугольник ABC — равнобедренный.

Доказательство:

Так как

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Соотношения в прямоугольном треугольнике
• Сумма углов треугольника
• Внешний угол треугольника
• Свойство точек биссектрисы угла
• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии
• Признаки равенства треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Применение правил на практике

Признаки равенства довольно важны для геометрии. Доказательства различных теорем построены именно на них. При этом с их помощью можно решать сложные задачи, связанные с многогранниками различных видов. Вот одно из таких заданий, для успешного решения которого нужно использовать правила равенства.

Имеется трапеция ABCD. В ней опущены высоты BK и CN. Известно, что AK = ND. Доказать, что заданная фигура равнобокая. Сделать это можно будет, установив, что 2 прямоугольных треугольника равны друг другу, то есть ABK и CND после совмещения друг с другом будут совпадать. Значит: AB = CD.

По условию AK = ND, при этом отрезки AD и BC параллельны между собой. Последнее следует из определения параллелограмма. Можно утверждать, что высоты BK и CN имеют одинаковую длину. Это известно из правила равенства расстояния между двумя параллельными прямыми. В результате получается, что в треугольниках равны между собой 2 стороны (катеты) и угол. Из равенства следует, что все элементы в треугольнике одинаковые, то есть ABK = CND, значит: AB = CD, что и требовалось доказать.

Ещё один пример. Пусть есть геометрическое тело ABCD. В нём ∠С и ∠D равны 90 градусов. Известно, что длина AC совпадает с AD. Нужно установить, какой отрезок фигуры будет равен BD. Сделать это можно следующим образом: если провести отрезок, соединяющий вершины A и B, получится 2 треугольника с прямыми углами. При этом гипотенуза у них будет общей. Но также по условию у них равны 2 катета. Опираясь на третий признак идентичности треугольников, можно утверждать, что ACB = ADB. Отсюда следует, что у них равны все противолежащие стороны. Значит: BD = CD. Задача решена.

Таким образом, при решении задач со сложными фигурами, можно вначале оценить их на возможность использования свойств и признаков треугольников. В частности, прямоугольного. Фигуры нужно научиться видеть и использовать их свойства. Ведь треугольные тела уникальные и помогают в ряде случаев намного упростить решение примеров.

Признаки равенства начинают изучать в седьмом классе, сразу же после ознакомления с простейшими видами геометрических тел. Причём эти правила пригодятся и в дальнейшем, на уроках по стереометрии и аналитической геометрии.

Равенство по катету и острому углу

Рассмотрим две следующие ситуации:

Даны $\bigtriangleup{ABC}$ и $\bigtriangleup{A_{1}B_{1}C_1}$. В них $AB=A_{1}B_1$, $\angle{B}=\angle{B_1}$.

Даны $\bigtriangleup{ABC}$ и $\bigtriangleup{A_{1}B_{1}C_1}$. В них $AB=A_{1}B_1$, $\angle{C}=\angle{C_1}$.

Иными словами, имеем случай, когда в прямоугольных треугольниках катеты соответственно равны и при этом так же равны острые углы — либо прилежащие к катету, либо ему противолежащие.

В обеих ли ситуациях можно заключать равенство прямоугольных треугольников?

Когда угол прилегает к катету

Если в прямоугольных треугольниках равны катет и прилежащий к нему угол, вне зависимости от того, о каком катете идет речь, равенство заключается по второму признаку равенства треугольников («по стороне и прилежащим к ней углам»)

Внимание на чертеж выше: каким бы ни был катет, к нему прилегает острый угол с одной стороны и прямой с другой

Из чего следует:

Когда угол противолежит катету

Противолежащий угол — уже не такая очевидная ситуация, как с углом прилежащим, однако все крайне просто, стоит только вспомнить $C_1$ о сумме двух острых углов прямоугольного треугольника. Раз $\angle{C}=\angle{C_1}$, то:

$$\angle{B}=90^\circ-\angle{C}\\\angle{B_1}=90^\circ-\angle{C_1}$$Откуда приходим к равенству углов $\angle{B}=\angle{B_1}$ и вновь признаку равенства по катету и прилежащему острому углу.

Нюанс о материалах по геометрии

В учебниках часто встречается только частная формулировка признака — через прилежащий острый угол. Однако на поверку выходит, что доказывать равенство по катету и острому углу можно без привязки к положению данного угла в прямоугольном треугольнике.

Прилежащий или противолежащий — если при этом дано равенство катетов, прямоугольные треугольники будут равны.

Геометрия 7 класс Решение задач на 1 признак равенства треугольников

Конспект урока по геометрии в 7 классе

Тема урока: Решение задач по теме «Первый признак равенства треугольников»

Цели урока:

— повторить определения треугольника, равных фигур, равных треугольников; понятия соответствующих элементов треугольника;

— рассмотреть первый признак равенства треугольников

— начать формирование умения по решению задач на первый признак равенства

треугольников;

— развивать геометрические представления учащихся о многообразии геометрических фигур;

Задачи урока: 

— Создать условия для формирования  умения  применять первый признак равенства треугольников при решении задач.

— Развивать логическое мышление, тренировать геометрическую зоркость, пространственное воображение.

— Воспитывать навыки самоконтроля; внимательность, аккуратность.

Формы работы на уроке:

 классно-урочная, индивидуальная, фронтальная.

Тип урока:комбинированный.

Технические средства обучениямультимедийный проектор, экран, презентация в программе PowerPoint (Приложение 1).

Ход урока:

1. Организационный момент: объявление темы и целей урока

2. Устная работа, актуализация знаний:

— Вспоминаем определение треугольника;

— Вспоминаем определение равных фигур;

— Вспоминаем определение равных треугольников;

— Решаем устно задачи по готовому чертежу:

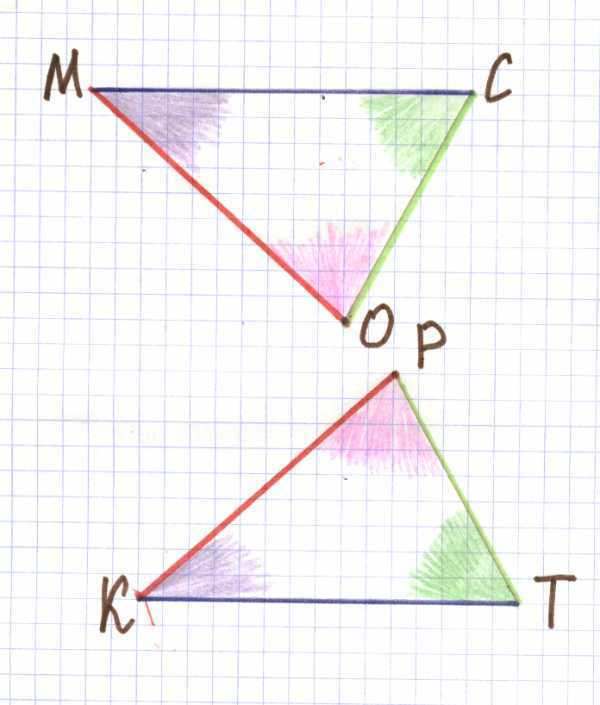
1. Назовите угол, лежащий напротив в стороны КТ в треугольнике МОС;

2. Назовите углы, прилежащие к стороне РТ треугольника КРТ;

3. Какой угол треугольника МОС соответствует углу Р треугольника РКТ;

4. Какая сторона треугольника РКТ соответствует стороне ОС треугольника МОС;

5. Какая сторона лежит напротив угла Т в треугольнике РКТ.

— Повторяем первый признак равенства треугольников.

3. Решение задач

Решаем задачи по готовым чертежам, представленным на экране. Один учащийся решает у доски, остальные в тетрадях.

1) Дано:

АВО и СDО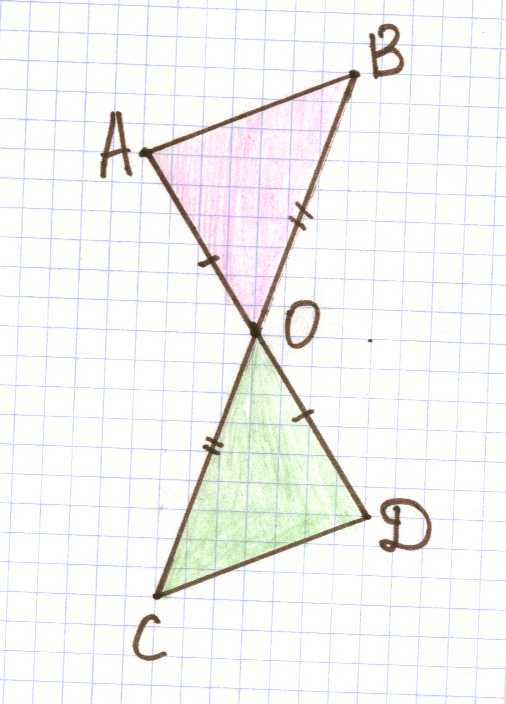

ВО=ОС

О — середина АD

АВ=3 см

ОСD=30*

——————————————

Доказать:

АВО = СDО

Найти:

СD, АВС

2) Дано: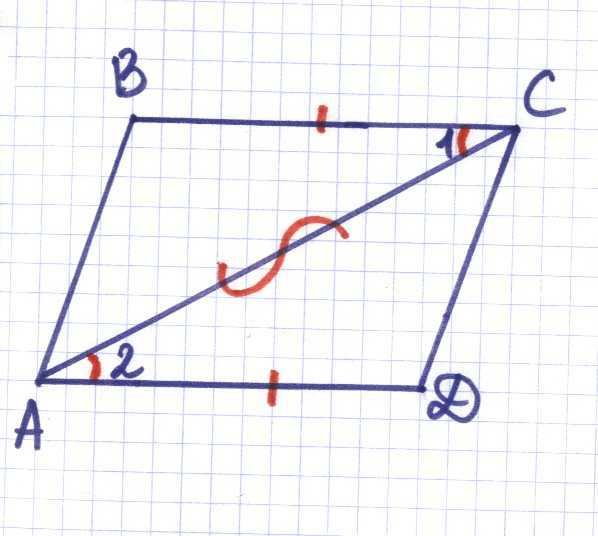

АВС, АСD

1= 2

АВ=2,5 см

ВС=АD

ВС в 1,2 р.б. АВ

———————————————

Найти:

Р АВСD

3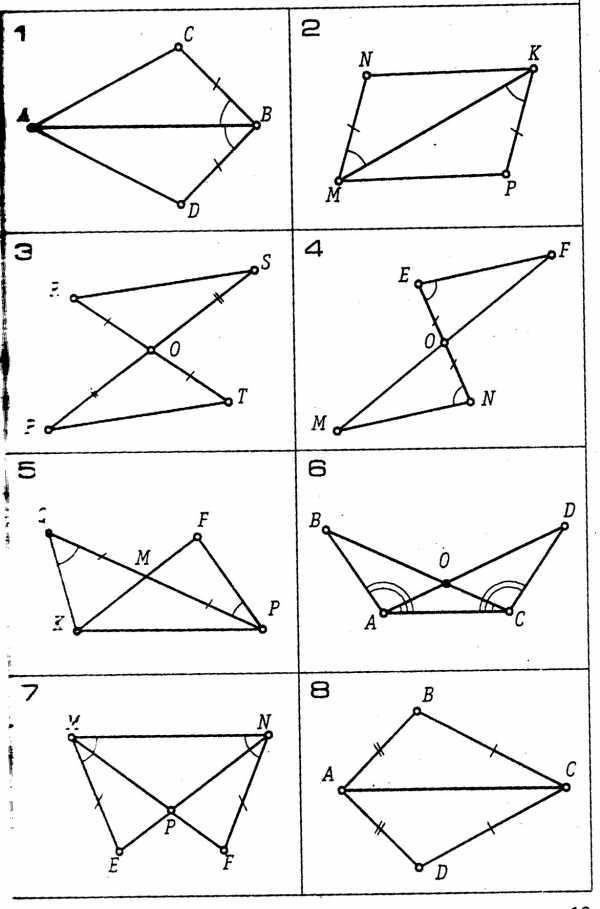

EMN и FNM

М = N

EM = FN

———————————-

Доказать:

EMN = FNM

4. Постановка д/з

1) Составить и решить задачу по готовому чертежу:

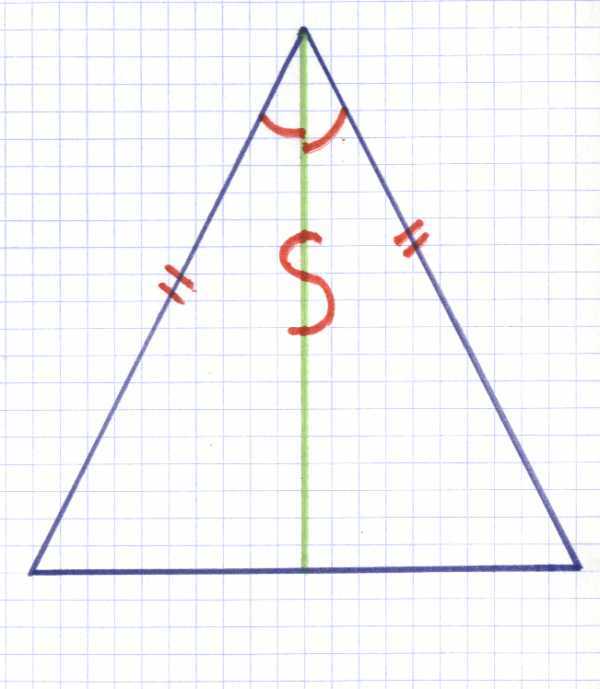
Признак равенства прямоугольных треугольников по гипотенузе и острому углу

Аналогичный метод размышления применим к случаю, когда в прямоугольных треугольниках равны соответственно гипотенузы и острый угол. На примере чертежа: либо $BC=B_{1}C_1$ и $\angle{\textcolor{purple}{B}}=\angle{\textcolor{purple}{B_1}},$ либо $BC=B_{1}C_1$ и $\angle{\textcolor{coral}{C}}=\angle{\textcolor{coral}{C_1}}$. По свойству $C_1$ прямоугольных треугольников о сумме острых углов:

Если $\angle{B}=\angle{B_1}$, то $\angle{C}=\angle{C_1}$, и наоборот.

Это позволяет сформулировать признак равенства прямоугольных треугольников по гипотенузе и острому углу:

{"questions":[{"content":"`image-1`Подытожим признаки равенства по катету и острому углу и по гипотенузе и острому углу. Если для пары прямоугольных треугольников известно, что у них соответственно равны катеты или гипотенузы, чтобы заключить их равенство, острый угол должен быть: `choice-5`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/10/test-dino-1.svg"},"choice-5":{"type":"choice","options":,"answer":}}}]}

Признаки равенства прямоугольных треугольников: задача на дополнительное построение

Дополнительное построение высоты в произвольных треугольниках, чтобы задействовать признаки равенства прямоугольных треугольников, — полезный инструмент. С его помощью можно доказывать равенство отрезков или углов. Давайте посмотрим, как этим пользоваться.

Задача. В остроугольном треугольнике $\bigtriangleup{ABC}$ на сторонах $AB$ и $AC$ отмечены точки $L$ и $K$ соответственно, причем $KL\parallel{BC}$ и $KL=KC$. На стороне $BC$ отмечена точка $M$ так, что $\angle{KMB}=\angle{BAC}$. Докажите, что $KM=AL$.

Дано:$\bigtriangleup{ABC}$$KL\parallel{BC}$$KL=KC$$\angle{KMB}=\angle{BAC}$

Найти:$KM=AL$

Решение

1. Рассмотрим параллельные прямые $KL$ и $BC$ и секущую $KC$. Согласно о соответственных углах $\angle{KCB}$ и $\angle{AKL}$ равны.

2. По условию треугольник $\bigtriangleup{ABC}$ остроугольный, следовательно $\angle{BAC}<90^\circ$. Тогда, поскольку $\angle{BAC}=\angle{KMB}$, угол $\angle{KMB}$ также является острым. По теореме о сумме смежных углов смежный с $\angle{KMB}$ угол $\angle{KMC}$ является тупым.

3. Проведем в треугольниках $\bigtriangleup{KMC}$ и $\bigtriangleup{ALK}$ высоты к сторонам $MC$ и $KA$. Угол $\angle{KMC}$ треугольника $\bigtriangleup{KMC}$ тупой, следовательно $\bigtriangleup{KMC}$ является тупоугольным. Высота в тупоугольном треугольнике проводится к . Отметим полученные высоты как $KD$ и $LF$ соответственно.

4. Рассмотрим треугольники $\bigtriangleup{LKF}$ и $\bigtriangleup{KDC}$. Они прямоугольные. Стороны $LK$ и $KC$ являются гипотенузами, при этом $\angle{LKF}=\angle{DCK}$ (соответственные при $KL\parallel{BC}$). Заключаем, что треугольники $\bigtriangleup{LKF}$ и $\bigtriangleup{KDC}$ равны (признак равенства прямоугольных треугольников по гипотенузе и острому углу).

5. Тогда высоты $LF$ и $KD$ равны как катеты в соответствующих равных прямоугольных треугольниках. Рассмотрим треугольники $\bigtriangleup{ALF}$ и $\bigtriangleup{KDM}$. Они прямоугольные. В них катеты $LF=KD$ и по условию $\angle{LAF}=\angle{DMK}$. Треугольники равны (равенство по катету и острому углу).

6. Поскольку  $\bigtriangleup{ALF}$ и $\bigtriangleup{KDM}$ равны, гипотенузы $AL$ и $KM$ также равны. Что и требовалось доказать.