Презентация на тему: » Теорема синусов Теорема. (Теорема синусов.) Стороны треугольника пропорциональны синусам противолежащих углов. Причем отношение стороны треугольника к.» — Транскрипт:
1
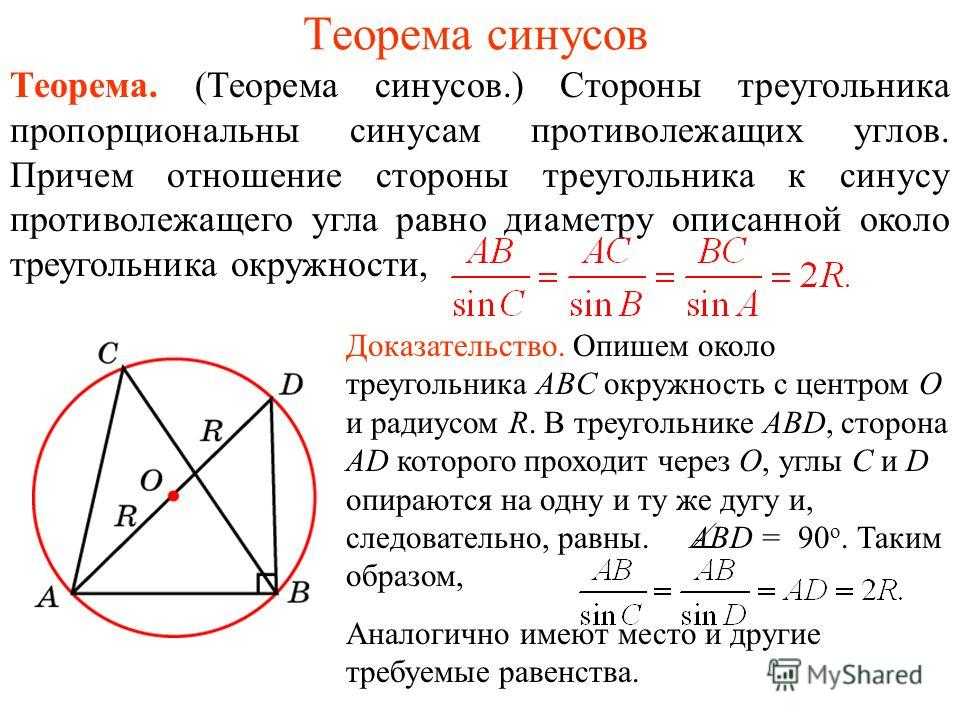
Теорема синусов Теорема. (Теорема синусов.) Стороны треугольника пропорциональны синусам противолежащих углов. Причем отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной около треугольника окружности, Доказательство. Опишем около треугольника ABC окружность с центром O и радиусом R. В треугольнике ABD, сторона AD которого проходит через O, углы C и D опираются на одну и ту же дугу и, следовательно, равны. ABD = 90 о. Таким образом, Аналогично имеют место и другие требуемые равенства.
2
Упражнение 1 Ответ: Угол B равен 45 о или 135 о. В треугольнике даны две стороны а = 3, b =, противолежащий стороне а угол А равен 30 о. Найдите угол B, лежащий против стороны b.
3
Упражнение 2 Ответ: 2 : 3 : 4. Стороны треугольника относятся как 2 : 3 : 4. Найдите отношения синусов углов этого треугольника.
4
Упражнение 3 Ответ: 3 : 4 : 5, прямоугольный. Синусы углов треугольника относятся как 3 : 4 : 5. Найдите отношение сторон этого треугольника. Какой это треугольник?
5
Упражнение 4 Найдите отношения сторон АС : ВС и АВ : ВС в треугольнике АВС, в котором: а) A = 120 о, B = 30 о ; б) A = 90 о, B = 30 о. Ответ: а) : 3, : 3;б) 1 : 2 и : 2.
6
Упражнение 5 Углы треугольника относятся как 1 : 2 : 3. Найдите отношение сторон. Ответ: 1 : : 2.
7
Упражнение 6 В треугольнике АВС АВ = 6 см, A = 45 о, С = 120 о. Найдите сторону BC. Ответ: см.
8
Упражнение 7 В треугольнике ABC сторона AB равна 4 см, угол C равен 150 о. Найдите радиус описанной окружности. Решение. Пусть O – центр описанной окружности треугольника ABC. Тогда угол AOB равен 60 о. Следовательно, треугольник AOB – равносторонний. Радиус описанной окружности равен 4. Ответ. 4.
9
Упражнение 8 Сторона AB треугольника ABC равна 10 см. Найдите радиус описанной около этого треугольника окружности, если противолежащий этой стороне угол C равен: а) 30 о ; б) 45 о ; в) 60 о ; г) 90 о ; д) 150 о. Ответ: а) 10 см; г) 5 см;д) 10 см. б) см; в) см;
10
Упражнение 9 Радиус окружности, описанной около треугольника ABC, равен 3 см. Найдите сторону AB этого треугольника, если противолежащий ей угол C равен: а) 30 о ; б) 45 о ; в) 60 о ; г) 90 о ; д) 150 о ? Ответ: а) 3 см;г) 6 см; д) 3 см. б) ;в) см;
11
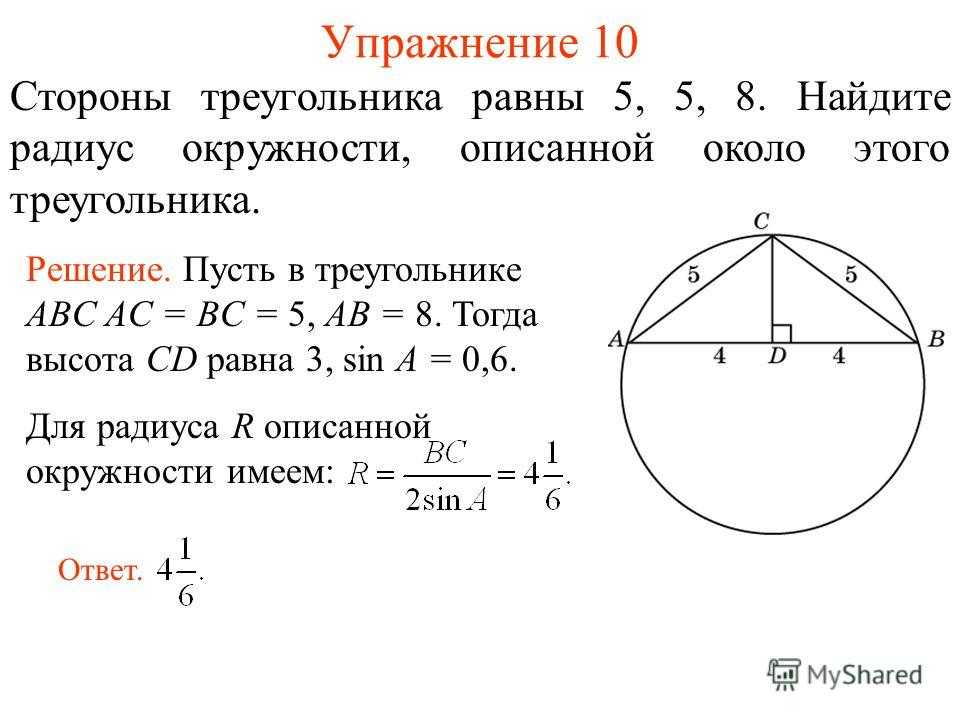
Упражнение 10 Стороны треугольника равны 5, 5, 8. Найдите радиус окружности, описанной около этого треугольника. Решение. Пусть в треугольнике ABC AC = BC = 5, AB = 8. Тогда высота CD равна 3, sin A = 0,6. Для радиуса R описанной окружности имеем: Ответ.
12
Упражнение 11 Две стороны треугольника равны 5 и 6. Высота, опущенная на его третью сторону, равна 4. Найдите радиус окружности, описанной около этого треугольника. Решение. Пусть в треугольнике ABC AC = 5, BC = 6, высота CD равна 4. Тогда sin A = 0,8. Для радиуса R описанной окружности имеем: Ответ.
13
Упражнение 12 Две стороны треугольника равны 4 и 6. Радиус описанной окружности равен 5. Найдите высоту, опущенную на третью сторону этого треугольника. Решение. Пусть в треугольнике ABC AC = 4, BC = 6, радиус R описанной окружности равен 5. Тогда sin A = 0,6 и высота CD равна 2,4. Ответ. 2,4.
14
Упражнение 13 Спортивный самолет летит по замкнутому треугольному маршруту с постоянной скоростью. Два угла этого треугольника равны по 30 о. Большую сторону он пролетел за 1 ч. За сколько времени он пролетит весь маршрут? Ответ: 2 ч 5 мин.
15
Упражнение 14 Используя рисунок, укажите способ нахождения расстояния d от точки A до недоступного объекта C. Ответ:
16
Упражнение 15 Используя рисунок, укажите способ нахождения высоты BC недоступного объекта. Ответ:
17
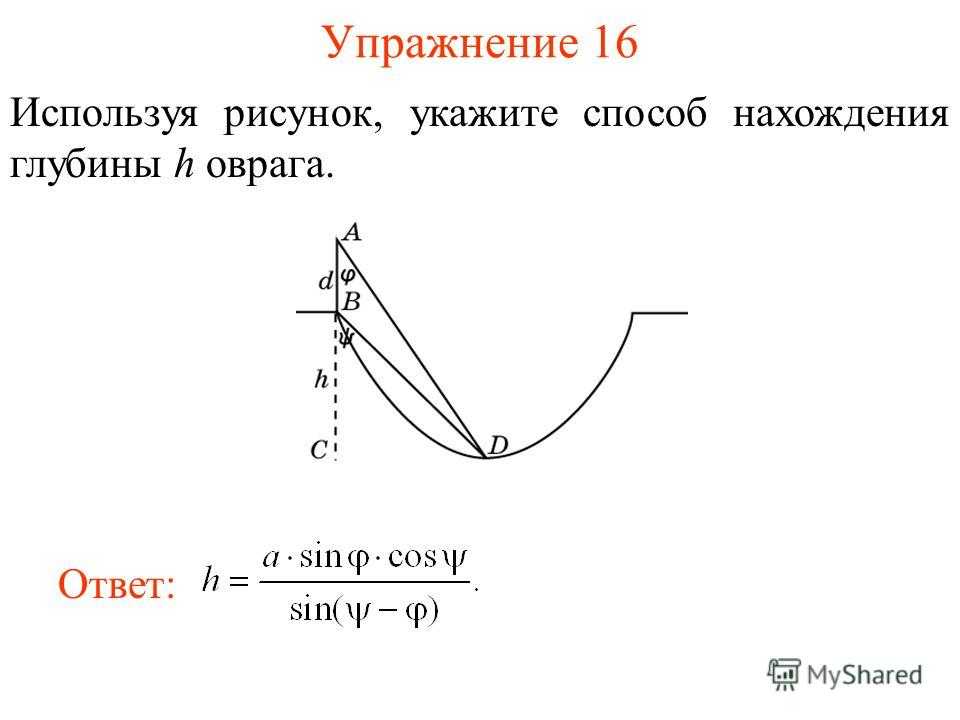
Упражнение 16 Используя рисунок, укажите способ нахождения глубины h оврага. Ответ:
18
Упражнение 17 Используя рисунок, укажите способ нахождения расстояния d между двумя недоступными объектами C и D. Ответ:
19
Упражнение 18 Используя рисунок, укажите способ нахождения угла, под которым видна башня CD из недоступного пункта B. Ответ:
20
Упражнение 19 Используя рисунок, укажите способ нахождения угла, под которым видна башня BD из вершины C башни AC. Ответ:
21
Упражнение 20 Используя рисунок, укажите способ нахождения угла, под которым виден участок дороги BD из недоступного пункта C. Ответ: Искомый угол теперь находится с помощью теоремы синусов, или теоремы косинусов.
Сумма углов треугольника. Теорема о сумме углов треугольника
Вначале рассмотрим непосредственно понятие треугольника.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками
(рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершин, а также три стороны.
Теорема о сумме углов в треугольнике
Введем и докажем одну из основных теорем, связанную с треугольников, а именно теорему о сумме углов в треугольнике.
Теорема 1
Сумма углов в любом произвольном треугольнике равняется $180^circ$.
Доказательство.
Рассмотрим треугольник $EGF$. Докажем, что сумма углов в этом треугольнике равняется $180^circ$. Сделаем дополнительное построение: проведем прямую $XY||EG$ (рис. 2)
- Так как прямые $XY$ и $EG$ параллельны, то $∠E=∠XFE$ как накрест лежащие при секущей $FE$, а $∠G=∠YFG$ как накрест лежащие при секущей $FG$
- Угол $XFY$ будет развернутым, следовательно, равняется $180^circ$.
- Получим
- $∠XFY=∠XFE+∠F+∠YFG=180^circ$
- Следовательно
- $∠E+∠F+∠G=180^circ$
- Теорема доказана.
Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
Теорема о внешнем угле треугольника
Еще одной теоремой о сумме углов для треугольника можно считать теорему о внешнем угле. Для начала введем это понятие.
Определение 4
Внешним углом треугольника будем называть такой угол, который будет смежным с каким-либо углом треугольника (рис. 3).
Рассмотрим теперь непосредственно теорему.
Теорема 2
Внешний угол треугольника равняется сумме двух углов треугольника, которые не являются смежным для него.
Доказательство.
Рассмотрим произвольный треугольник $EFG$. Пусть он имеет внешний угол треугольника $FGQ$ (рис. 3).
- По теореме 1 ,будем иметь, что $∠E+∠F+∠G=180^circ$, следовательно,
- $∠G=180^circ-(∠E+∠F)$
- Так как угол $FGQ$ внешний, то он смежен с углом $∠G$, тогда
- $∠FGQ=180^circ-∠G=180^circ-180^circ+(∠E+∠F)=∠E+∠F$
- Теорема доказана.
Пример задач
Пример 1
Найти все углы треугольника, если он является равносторонним.
Решение.
Так как у равностороннего треугольника все стороны равны, то будем иметь, что и все углы в нем также равны между собой. Обозначим их градусные меры через $α$.
- Тогда, по теореме 1 будем получать
- $α+α+α=180^circ$
- $3α=180^circ$
- $α=60^circ$
- Ответ: все углы равняются по $60^circ$.
Пример 2
- Найти все углы равнобедренного треугольника, если один его угол равняется $100^circ$.
- Решение.
- Введем следующие обозначения углов в равнобедренном треугольнике:
Так как нам не дано в условии, какой именно угол равняется $100^circ$, то возможны два случая:
-
- Угол, равный $100^circ$ — угол при основании треугольника.
- По теореме об углах при основании равнобедренного треугольника получим
- $∠2=∠3=100^circ$
Но тогда только их сумма будет больше, чем $180^circ$, что противоречит условию теоремы 1. Значит, этот случай не имеет места.
-
Угол, равный $100^circ$ — угол между равными сторонами, то есть
$∠1=100^circ$
- Так как треугольник равнобедренный, то $∠2=∠3$,
- По теореме 1, получим
- $∠1+∠2+∠3=180^circ$
- $2∠2+100^circ=180^circ$
- $2∠2=80^circ$
- $∠2=40^circ$
- Ответ: $40^circ$, $40^circ$, $100^circ$.
Пример 3
Найти угол $XZO$ на рисунке 4, если $∠XOZ=45^circ$, а $∠Y=25^circ$
- Решение.
- Так как у равнобедренного треугольника углы при основании равны, то получим, что $∠X=∠Y=25^circ$
- Из треугольника $XOZ$, по теореме 1, получим
- $∠X+∠XOZ+∠XZO=180^circ$
- Тогда
- $∠XZO=180^circ-∠X-∠XOZ=180^circ-25^circ-45^circ=110^circ$
- Ответ: $110^circ$.
Пример 4
- Найти угол $XOZ$ на рисунке 4, если $∠XZO=45^circ$, а $∠Y=25^circ$
- Решение.
- Так как у равнобедренного треугольника углы при основании равны, то получим, что $∠X=∠Y=25^circ$
- Из треугольника $XYZ$, по теореме 1, получим
- $∠X+∠Y+∠Z=180^circ$
- $∠Z=180^circ-∠X-∠Y=180^circ-25^circ-25^circ=130^circ$
- $∠OZY=∠Z-∠XZO=130^circ-45^circ=85^circ$
- По теореме 2, получим
- $∠XOZ=∠OZY+∠Y=85^circ+25^circ=110^circ$
- Ответ: $110^circ$.
Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: АВС (рис. 220).
Доказать: A+B +C = 180°.
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда KBA =A как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей АВ, aMBC =C как внутренние накрест лежащие углы при параллельных прямых КМ и АС и секущей ВС. Так как углы КВА, ABC и МВС образуют развернутый угол, то
KBA +ABC +MBC = 180°. ОтсюдаA +B +C = 180°. Теорема доказана.
Следствия.
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то1 =2.
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть ( — градусная мера одной части).
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если то, рассуждая аналогично, получим формулу: Если, например,
Пример:
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, (рис. 226).
Докажем, чтоACB = 90°. Обозначим A = ,В = . Так как медиана делит сторону пополам, то AM = MB = АВ. Тогда СМ=АМ=МВ. Так как АМС — равнобедренный, тоA =ACM = как углы при основании равнобедренного треугольника. Аналогично, СМВ — равнобедренный и B =BCM = . Сумма углов треугольника ABC, с одной стороны, равна 2 + 2, с другой — равна 180°. Отсюда 2 + 2 = 180°, 2( + ) = 180°, + = 90°. НоACB = + , поэтому
ACB = 90°.
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) C=90°,A=,B=.
Проведем отрезок СМ так, чтоACM=, и докажем, что СМ — медиана и что СМ=АВ. Угол В дополняет угол А до 90°, aBCM дополняетACM до 90°. Поскольку ACM =A = , тоBCM =. Треугольники АМС и ВМС — равнобедренные по признаку равнобедренного треугольника. Тогда AM = МС и МВ = МС. Отсюда СМ — медиана и СМ = АВ.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
«Параллельность прямых. Решение задач». 7-й класс
Разделы: Математика
Класс: 7
— продолжить работу над формированием у учащихся базовых теоретических и практических навыков по данной теме (организовать отработку теоретических и практических знаний учащихся по теме “параллельность прямых”);
— продолжить знакомство с различными методами решения задач, организовать работу по составлению алгоритма (способа), схемы рассуждений при решении задач;
1. Организационный момент. Актуализация опорных знаний.
Сегодня мы продолжим изучать тему “Параллельность прямых”.
Давайте вспомним, на каких вопросах мы останавливались:
— определение параллельных прямых;
— следствия из аксиомы параллельности;
— свойства параллельных прямых;
Виды углов:1 и 4, 5 и 6, 7 и 6, 1 и 9, 4 и 11, 3 и 9, 2 и 11, 3 и 10, и т.д.
Сейчас вы в течение 2-3х минут повторяете теоретический материал по обучающим карточкам. (Обучающие карточки представляют собой двухсторонние карточки, на одной стороне которых записывается начало теоремы, следствия, свойства, а на оборотной стороне продолжение. Учащийся начинает формулировать теорему, следствие, свойство не переворачивая карточку, затем переворачивает и проверяет себя. Если все верно, кладет карточку справа от себя, если допустил ошибки, кладет слева. Когда проговорит весь теоретический материал, берет карточки слева и проговаривает снова. И т.д.)
Сколько неверных вариантов осталось по истечении времени?
Каждый из вас знает, какие теоретические вопросы ему нужно повторить ещё раз к следующему уроку. (Таким образом, ученик сам оценивает уровень своей теоретической подготовки по данной теме).
2. Новый материал.
Мы за время с начала урока повторили теоретический материал: определения, свойства, признаки, виды углов.
Как вы думаете, для чего мы всё это повторили? Где все это нам необходимо применять?
При решении задачи
— Записываем число и тему урока в тетрадь.
— А какие именно задачи мы будем решать?
— Где необходимо доказать параллельность прямых или использовать свойства параллельных прямых?
— Каким образом мы можем подойти к параллельности прямых?
— Через равенство углов (какие признаки конкретно к каким углам: односторонние, накрест лежащие, соответственные)?
— Т.е. нам необходимо иметь равные углы (накрест лежащие или соответственные) или дающие вместе 180°. С какими фигурами мы обычно работали, доказывая равенство углов?
— Доказывали, что треугольники равны, а затем делали вывод о равенстве необходимых сторон или необходимых углов.
— Составим схему рассуждения при решении задач на доказательство параллельности прямых:
— найти углы, необходимые для решения;
— доказать равенство треугольников, в которые эти углы входят;
— сделать вывод о параллельности прямых на основании признака параллельности.
3. Решение задач.
— Сформулируйте задачу на доказательство равенства треугольников по данному чертежу.
— Попробуйте сформулировать вопрос (из новой темы) (на доказательство параллельности прямых).
(Учащиеся формулируют вопрос)
3) прямые параллельны,
4) другие углы —> те же прямые.
— Cформулируйте текст задачи и вопрос (из старой темы) (на равенство треугольников).
— Cформулируйте вопрос (из новой темы) (на доказательство параллельности прямых).
3) прямые параллельны,
4) другие углы —> те же прямые.
По вариантам записать решение (до 3-4 минут).
Вместе с классом проверяют решение (чтение вслух и обсуждение). Можно решение вывести на слайд и попросить учащихся оценить себя по эталону.
Итогом работы является заполненная таблица с пошаговым алгоритмом решения задач.
| 1 | Выбрать треугольники, в которых находятся прямые, параллельность которых необходимо доказать |
| 2 | Доказать равенство треугольников. |
| 3 | Выбрать нужные углы (накрест лежащие, соответственные, односторонние ) |
| 4 | Доказать параллельность, используя нужный признак |
4. Этап первичного практического закрепления
Учащиеся работают с тестами (приложение , )
Сумма углов треугольника — урок. Геометрия, 7 класс
Сумма углов треугольника равна (180°).
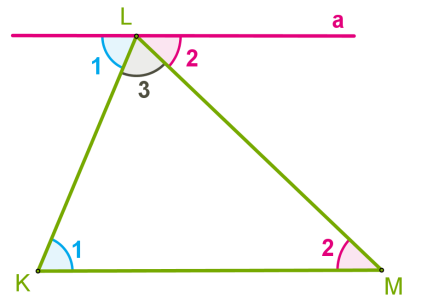
- Доказательство
- Рассмотрим произвольный треугольник (KLM) и докажем, что ∡ (K) (+) ∡ (L) (+) ∡ (M =) 180°.
- Проведём через вершину (L) прямую (a), параллельную стороне (KM).
- Углы, обозначенные (1), являются накрест лежащими углами при пересечении параллельных прямых (a) и (KM) секущей (KL), а углы, обозначенные (2) — накрест лежащими углами при пересечении тех же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е. ∡ (1) (+) ∡ (2) (+) ∡ (3 =) 180°, или ∡ (K) (+) ∡ (L) (+) ∡ (M =) 180°.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
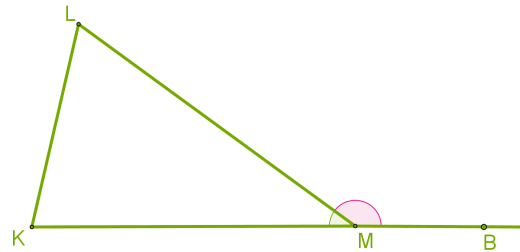
Доказательство
Из равенств ∡ (KML) (+) ∡ (BML=) 180° и ∡ (K) (+) ∡ (L) (+) ∡ (KML =) 180° получаем, что ∡ (BML =) ∡ (K) (+) ∡ (L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
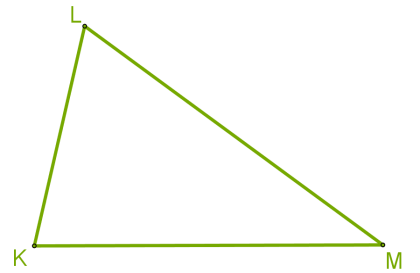
У треугольника (KLM) все углы острые.
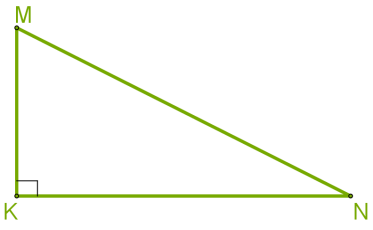
- У треугольника (KMN) угол (K = 90)°.
- У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
- На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.
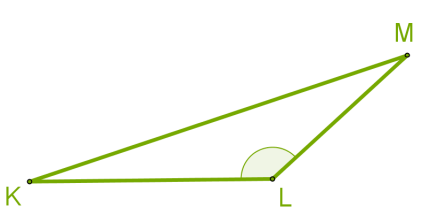
У треугольника (KLM) один угол тупой.
Геометрия 7 класс объяснение основных тем, понятно для детей
первые геометрические объекты
Начать стоит с самого понятия «геометрия». С древнегреческого слово переводится как земля и измерение. Эта древнейшая наука, которая появилась в связи с необходимостью строить здания, дороги, измерять объекты и прокладывать границы.
Первыми геометрическими фигурами, которые стоит усвоить, являются точка, прямая, отрезок.
Точка — это абстрактный объект в пространстве. Никаких измерительных характеристик она не имеет (но можно определить координаты).
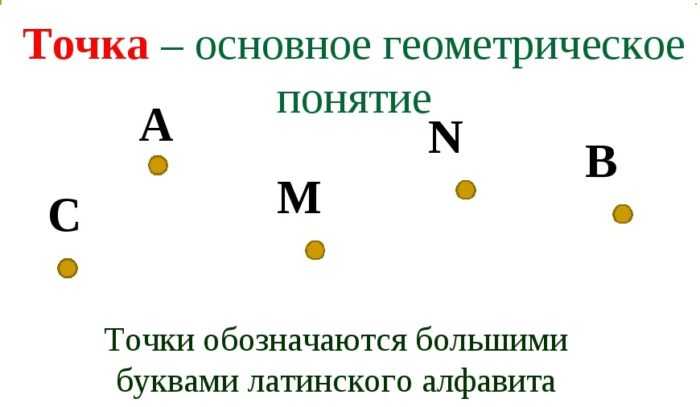Через две точки можно провести прямую линию (причем единственную); она не искривляется, не имеет конца и начала, продолжается до бесконечности.
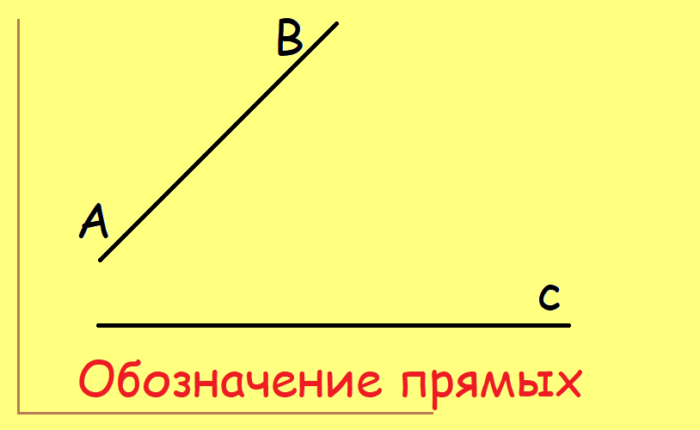
Иными словами, прямая — это множество точек на одной линии, продолжающееся до бесконечности.
Запомните важную аксиому:
Если часть прямой линии ограничить точками, получится отрезок. У отрезка есть и начало, и конец. Обозначается он большими буквами (например, отрезок КL, SD, AB и т.д.).
Если две прямые пересекаются под углом 90º, то говорят, что они перпендикулярны.
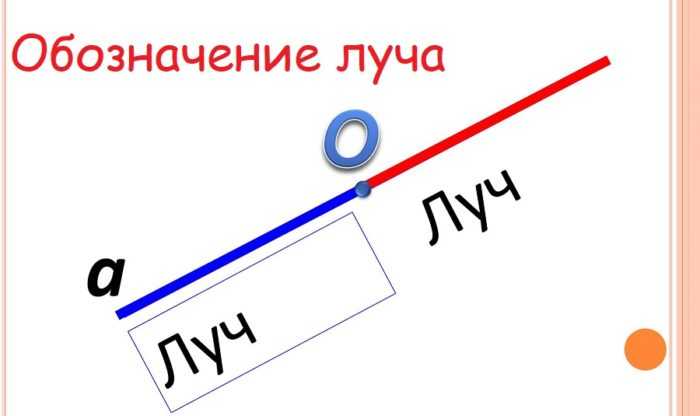
Если прямую ограничить только одной точкой, то получится два луча. У луча есть начало, а конца нет (уходит в бесконечность). Называют луч двумя буквами, например, ОА.
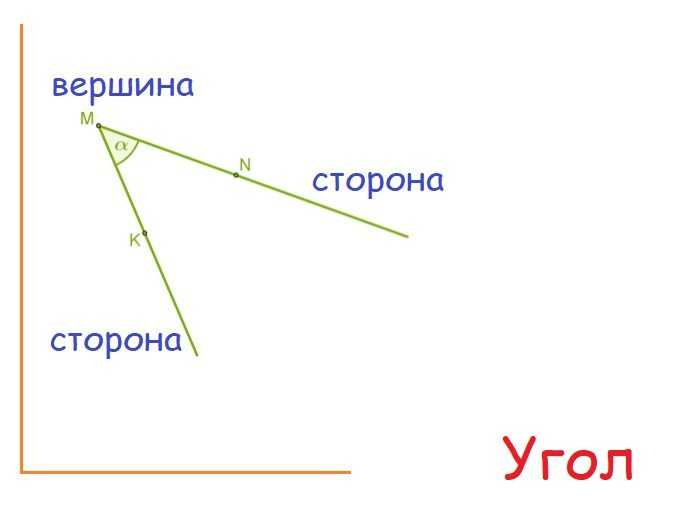
Еще одна фигура — угол. Он представляет собой точку и два луча, исходящие из нее. Лучи — это стороны угла, а начало этих сторон — его вершина. От того, сколько градусов составляет угол, зависит тип треугольника, который можно образовать.
https://youtube.com/watch?v=pMICc6Zxh3M
О равных треугольниках. Равнобедренный треугольник
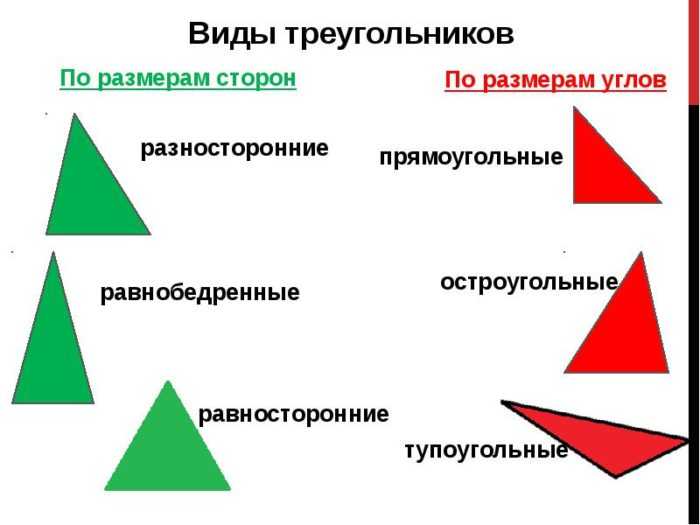
Треугольником принято считать фигуру, которая состоит из 3-х точек. Причем точки эти не должны лежать на одной прямой, а соединяются они отрезками.
Треугольники можно различать по двум признакам: размеру сторон и размеру углов.
Если один треугольник (назовем его CFD) наложить на другой (C1F1D1) и они будут соответствовать друг другу, то треугольники равны. У равных фигур все элементы равны.
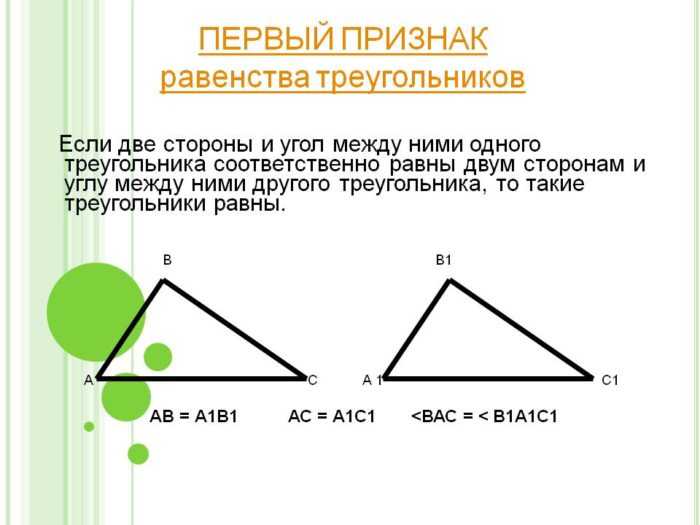
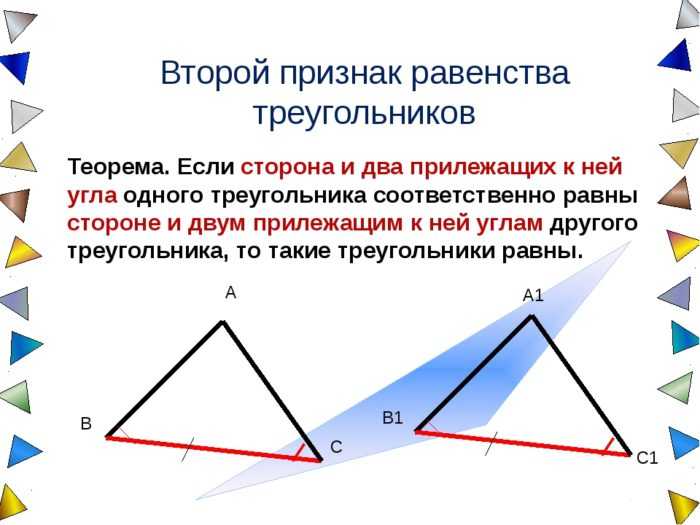
Чтобы понять, равны ли треугольники, познакомимся с признаками равенства этих фигур.
Остановимся отдельно на равнобедренных треугольниках. Если 2 стороны треугольники равны, то его называют равнобедренным.
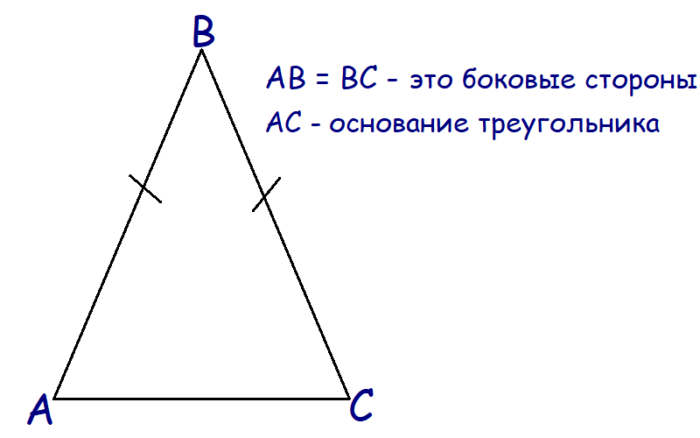
Исходя из этого, можно выделить признаки равнобедренного треугольника. Треугольник равнобедренный, если:
- 2 угла в нем равны;
- биссектриса одновременно является высотой и медианой;
- медиана — биссектриса и высота;
- высота, соответственно — медиана и биссектриса.
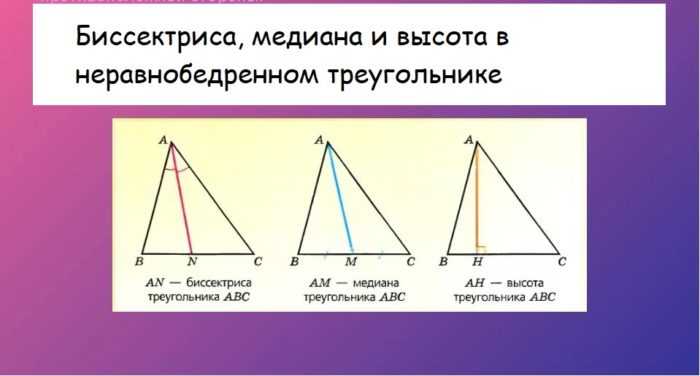
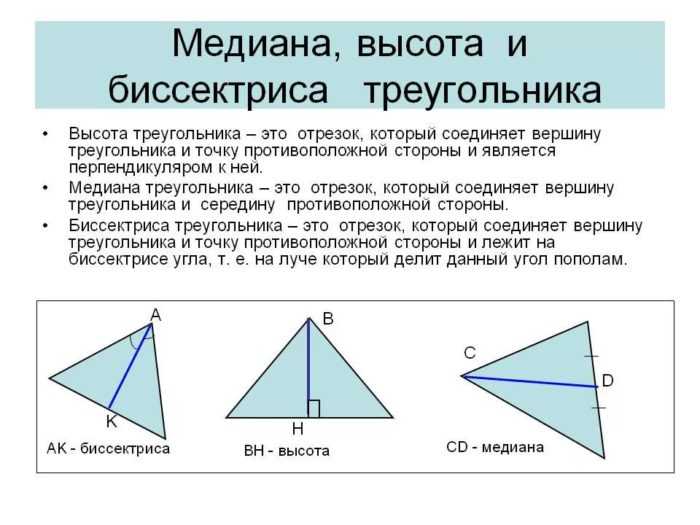Если взять треугольник неравнобедренный, то эти три составляющие (высота, биссектриса и медиана) не будут совпадать (это четко прослеживается на рисунке ниже).
параллельные прямые
Если на тетрадном листе кажется, что прямые параллельны, но имеется небольшой уклон, то вполне вероятно, что за пределами листа (ведь они бесконечны), прямые пересекутся.
Чтобы понять, параллельны ли прямые, нужно усвоить 3 основных признака.
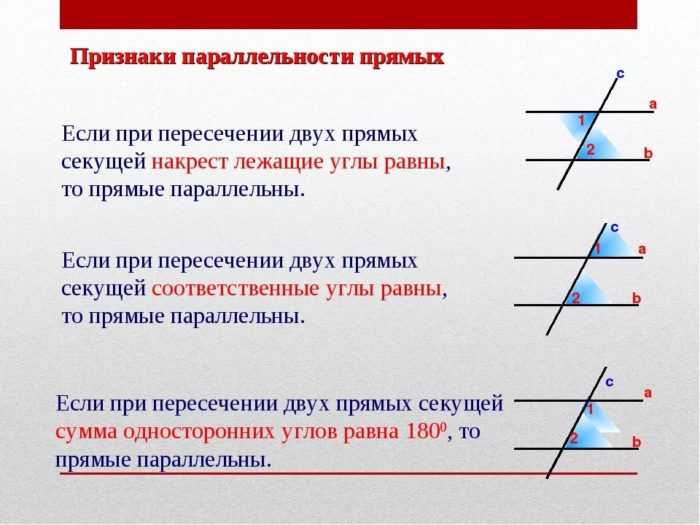Показать параллельность прямых а и б можно так: а ΙΙ б.
О многоугольнике с тремя сторонами
Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.
Таким образом, два ключевых элемента образуют рассматриваемую фигуру:
- вершина;
- сторона.
И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.
На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.
Существование фигуры
Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.
Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.
Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:
- Остроугольные. В них все три угловые меры меньше 90 °. При этом возможны случаи взаимного их равенства, то есть каждый будет составлять 60 °. Такие треугольники называются равносторонними или правильными. Равны могут быть между собой также два угла, это будет уже равнобедренный треугольник, у которого боковые стороны имеют одинаковую длину.
- Тупоугольные. Поскольку сумма составляет 180 °, то по определению в рассматриваемом многоугольнике не может быть больше одного тупого угла. Тупоугольные фигуры могут иметь либо произвольный тип, когда все их отрезки различаются, либо являться равнобедренными.
- Прямоугольные. Это специальный тип треугольников, о котором известно многое, и который разграничивает два предыдущих типа. В них один угол равен 90 °, а два других являются острыми.
Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.
Важные линии
Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:
- Медиана — делящий на две равные по площади части исходный треугольник. Отрезок проводится из вершины к середине противоположной стороны.
- Биссектриса. Ею называют отрезок, который на две половины делит угол при произвольной вершине.
- Высота. Этот элемент проводится также из вершины, но по отношению к противоположной стороне он является перпендикуляром. Таким образом, высота делит исходную фигуру на два прямоугольных геометрических объекта, которые в общем случае между собой не равны.
- Медиатриса — это серединный перпендикуляр, то есть он сочетает свойства медианы и высоты, однако, через вершину треугольника он может не проходить. Медиатрисами пользуются при построении описанной окружности.
- Средняя линия — это отрезок, который посередине пересекает две стороны треугольника. Его длина всегда будет в два раза меньше стороны фигуры, которой он параллелен. Средняя линия приводит к созданию подобной исходной фигуры, которая в два раза меньше.
Правило встречается в следующих упражнениях:
7 класс
Задание 223, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 242, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 334, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 362, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 637, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 719, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 854, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1058, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1279, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сравнение сторон и углов треугольника
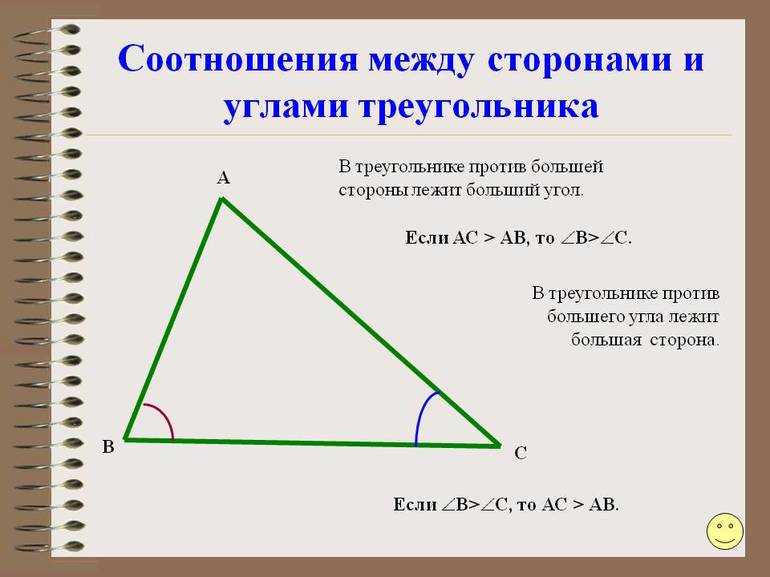
Докажем следующую теорему:
Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B:
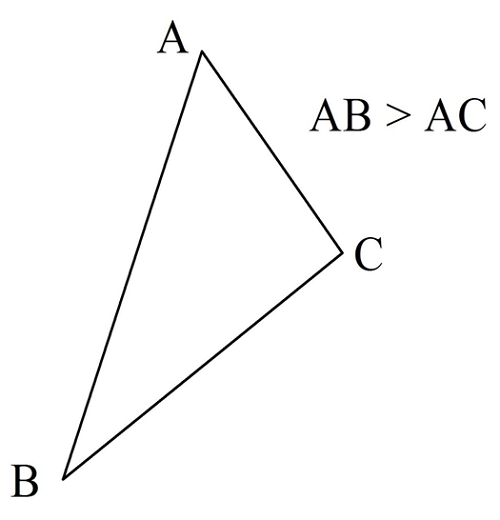
Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком:
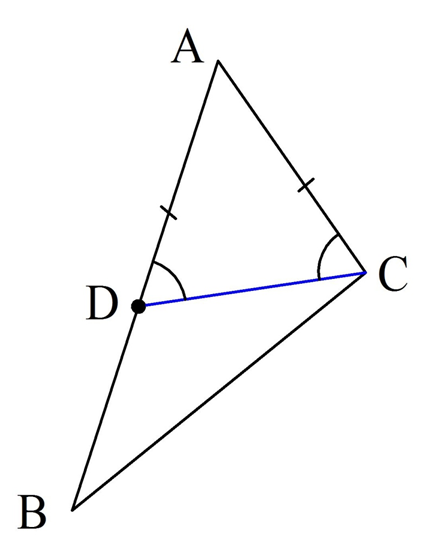
Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD.
Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что
Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ <ВС. Первый вариант означает, что ∆АВС – рав-бедр., но тогда ∠С =∠B, что противоречит условию. Если же АВ <ВС, то по только что доказанному утверждению ∠С<∠B, что также противоречит исходному условию. Поэтому АВ >AC.
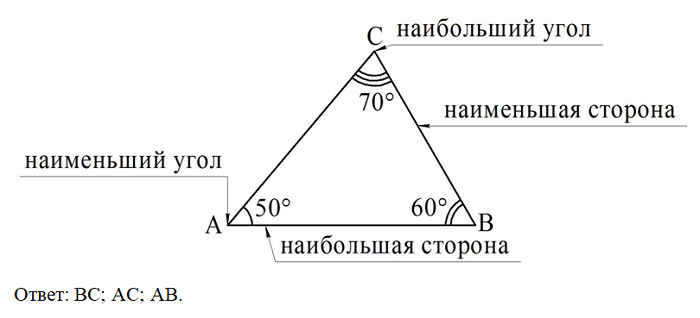
Задание. В ∆АВС известны углы:
Запишите стороны этого треуг-ка в порядке возрастания.
Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС<AС<AВ:
Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка:
Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно.
Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр.
Решение.
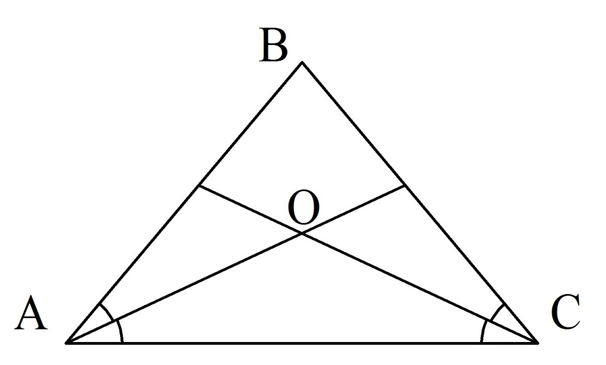
Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса:
В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС).