Назначение и свойства логарифмов, алгоритм решения задач с примерами

Графические логарифмические функции: примеры

Графики
Логарифмические функции: примеры (стр.
2 из 3)

В предыдущем
например, я сказал
было два варианта построения графиков журналов. Предыдущая страница продемонстрировала
как работать от логарифмов, чтобы найти интересные точки
участок.Однако есть другой вариант: вы можете использовать свой калькулятор для
найти точки сюжета.

Кому найти мои точки сюжета с помощью моего калькулятора (поскольку мой калькулятор может вычислять только общие журналы или журналы с основанием 10 и естественные журналы или журналы с основанием e), Мне нужно будет использовать смену базы формула, что дает мне эквивалентное уравнение.Исходное уравнение, л = журнал 2 ( x ) становится и = лн ( x ) / лн (2) :
Один раз Я ввел форму уравнения, удобную для калькулятора, я могу получить некоторые точки сюжета из функции ТАБЛИЦА моего калькулятора: Авторские права Элизабет Стапель 2002-2011 Все права защищены (Если у вас старый ТИ-85, значит, у вас нет встроенного «ТАБЛИЦА» утилита, вы можете установить любую из различных программ послепродажного обслуживания которые делают то же самое.Графика справа — экран кадры того, что программа на моем ТИ-85 выпускается.) I знаю, что у меня должны быть все положительные значения в журнале, поэтому я начать листинг ТАБЛИЦЫ с x = 1 и перейти от там.
Я бы все еще хотелось бы, чтобы точки на графике находились между нулем и единицей, поэтому я отрегулируйте начальное («начальное») значение и приращение (количество «рассчитывать по»), чтобы получить дополнительный сюжет точки между x = 0 и x = 1:

Использование эти точки (с точностью до одного или двух десятичных знаков), Я получу тот же график, что и раньше.

В зависимости
в программном обеспечении вашего калькулятора вы либо получите пустые места в вашем
ТАБЛИЦА для значений и когда x = 0 и когда x отрицательный; или
слот будет отображать «ERROR», «UNDEFINED» или другое
код ошибки; иначе программа выйдет из строя.(Mine вылетает из-за undefined и — значения,
вот почему я был осторожен, чтобы начать отображение ТАБЛИЦЫ выше с положительного x -знач.)
Такое поведение в функции ТАБЛИЦА подтверждает тот факт, что логарифмы
не определены для неположительных аргументов.

(относительно
поиск точек графика между x = 0 и x = 1, если вы этого не сделаете
знать, как изменить исходное значение с x = 0 или как изменить
ваше приращение от 1,
обратитесь к руководству по эксплуатации; инструкции будут где-то в
глава по построению графиков.)

Если вы строите график
общий (основание-10)
бревно или натуральное (основание — е )
log, просто используйте свой калькулятор, чтобы получить точки сюжета. При работе с
общий журнал, вы быстро достигнете слишком больших чисел, если вы
старайтесь наносить только целые точки; например, чтобы получить как
высота y = 2, вам нужно будет
использовать x = 100, и ваш график
было бы смехотворно широким.При работе с натуральным бревном основание e в любом случае это иррациональное число, так что даже не имеет смысла пробовать чтобы найти красивые аккуратные точки сюжета, потому что, кроме (1,
0) их нет.

Иногда
график журнала немного смещен из «обычного» положения (показано
на графике выше) вверх, вниз, вправо, влево или вверх ногами, или
еще какая-то их комбинация.Но общий вид графика имеет тенденцию
оставаться таким же.

Это основной журнал
график, но он сдвинут
вверх на два
единицы. Чтобы найти точки для этого графика, я вставлю полезные значения
из x (будучи степенью 3,
из-за основания журнала), а затем я упрощу для соответствующего
значения и .

3 = 1, поэтому журнал ₃ (1) = 0, и журнал ₃ (1)
+ 2 = 2 3 1 = 3, поэтому журнал ₃ (3) = 1, и журнал ₃ (3)
+ 2 = 3 3 2 = 9, поэтому журнал ₃ (9) = 2, и журнал ₃ (9)
+ 2 = 4 3 3 = 27, поэтому журнал ₃ (27) = 3, и журнал ₃ (27)
+ 2 = 5

Движение в обратном направлении
(чтобы получить значения и для x от 0 до
1):

3 1 = 1 / ₃ , поэтому журнал ₃ ( 1 / ₃ ) = 1, и журнал ₃ ( 1 / ₃ ) + 2 = 1 3 2 = 1 / ₉ , поэтому журнал ₃ ( 1 / ₉ ) = 2, и журнал ₃ ( 1 / ₉ ) + 2 = 0 3 3 = 1 / ₂₇ , поэтому журнал ₃ ( 1 / ₂₇ ) = 3, и журнал ₃ ( 1 / ₂₇ ) + 2 = 1

Это единственные «аккуратные»
точки, которые я собираюсь найти для своего графика.Если я чувствую необходимость
для дополнительных точек графика, особенно между любыми двумя точками
Я нашел выше, я могу оценить функцию « ln ( x )
/ пер. (3) »
в моем калькуляторе.

График г = журнал 3 ( x ) + 2 выглядит так:

1
| 2 | 3 | Возвращение
к указателю Вперед >>

Цитируйте эту статью как:

Стапель, Елизавета.«Графические логарифмические функции: примеры». Пурпурная математика . Доступно по номеру https://www.purplemath.com/modules/graphlog2.htm . Доступ 2016 г.

Функции десятичного логарифма

Натуральный логарифм

Натуральный логарифм, или натуральный логарифм, является функция логарифм которой производная является обратной функцией определяется в  : .
р+*{\ Displaystyle \ mathbb {R} _ {+} ^ {*}}р{\ Displaystyle \ mathbb {R}}Икс↦1Икс{\ displaystyle x \ mapsto {\ frac {1} {x}}}

Функция Непера условно обозначается «  ln  » или «  log  », обозначение, обычно используемое в теории чисел и информатике.

Основание функции натурального логарифма, обозначаемой е , называется числом Непера или числом Эйлера.

Приблизительное значение:

е≈2 718{\ displaystyle \ mathrm {e} \ приблизительно 2 {,} 718}.

Десятичный логарифм

Это наиболее практичный логарифм в ручных числовых вычислениях, он обозначается как log или log ₁₀ . Стандарт ISO 80000-2 гласит, что log ₁₀ следует обозначать как lg , но это обозначение используется редко.

Его можно найти при создании логарифмических шкал , полулогарифмических или логарифмических эталонных показателей , в логарифмической линейке , при вычислении pH в децибелах .

Он указывает, в какую степень необходимо возвести 10, чтобы найти начальное число: изображение числа в бревне — это относительное целое число, до которого необходимо возвести 10, чтобы получить антецедент . Например :

В базе 10:

бревно10⁡(10)знак равно1 так как 101знак равно10{\ displaystyle \ log _ {10} (10) = 1 {\ text {char}} 10 ^ {1} = 10}

бревно10⁡(100)знак равно2 так как 102знак равно100{\ displaystyle \ log _ {10} (100) = 2 {\ text {car}} 10 ^ {2} = 100}

бревно10⁡(1000)знак равно3 так как 103знак равно1000{\ displaystyle \ log _ {10} (1000) = 3 {\ text {car}} 10 ^ {3} = 1000}

бревно10⁡(,01)знак равно-2 так как 10-2знак равно,01{\ displaystyle \ log _ {10} (0,01) = — 2 {\ text {char}} 10 ^ {- 2} = 0,01}

Значение логарифма чисел, отличных от степени 10, требует приблизительного расчета. Например, расчет log (2) можно выполнить вручную, отметив, что 2 10 ≈ 1000, следовательно, 10 log ₁₀ (2) ≈ 3, следовательно, log ₁₀ (2) ≈ 0,3 .

Для любого строго положительного действительного b, отличного от 1, и для любого действительного x > 0 ,

бревноб⁡(Икс)знак равнобревно10⁡(Икс)бревно10⁡(б){\ displaystyle \ log _ {b} (x) = {\ frac {\ log _ {10} (x)} {\ log _ {10} (b)}}}.

Двоичный логарифм

Стандарт ISO 80 000 рекомендует, чтобы фунт был логарифмом по основанию 2.

Двоичный логарифм, особенно используемый при вычислении музыкальных интервалов из соотношения частот , для получения октав , полутонов или центов , нашел гораздо большее применение в информатике . В компьютерах, работающих в двоичной системе , вычисление логарифма по основанию 2 является наиболее точным и эффективным алгоритмом.

Число x, закодированное в двоичной системе с плавающей запятой, разлагается на мантиссу m между 1 (включительно) и 2 (исключая) и показатель степени p , указывающий степень 2, которая умножает мантиссу для получения числа. Показатель степени — это целая часть двоичного логарифма, а двоичный логарифм мантиссы находится в диапазоне от 0 (включительно) до 1 (исключено).

Иксзнак равно2п×м⟹фунт(Икс)знак равноп+фунт(м).{\ displaystyle x = 2 ^ {p} \ times m \ Longrightarrow {\ textrm {lb}} (x) = p + {\ textrm {lb}} (m).}

Это возвращает вычисление к вычислению двоичного логарифма числа от 1 (включительно) до 2 (исключено). Если мы умножаем это число на себя, и результат превышает 2, это число больше √2: следующая цифра после десятичной точки равна 1, в противном случае — 0. Мы продолжаем итерацию до желаемой точности. достигается.

Два предыдущих логарифма выводятся из этого следующим образом:

пер⁡(Икс)знак равнолб(Икс)лб(е) а также бревно10⁡(Икс)знак равнолб(Икс)лб(10){\ displaystyle \ ln (x) = {\ frac {\ mathrm {lb} (x)} {\ mathrm {lb} (\ mathrm {e})}} {\ text {and}} \ log _ {10} (x) = {\ frac {\ mathrm {lb} (x)} {\ mathrm {lb} (10)}}}.

Кологарифм

Отрицательный логарифм числа является отрицательным логарифмом этого числа и логарифм его обратным: .
одеколонб⁡Иксзнак равно-бревноб⁡Иксзнак равнобревноб⁡1Икс{\ displaystyle \ operatorname {colog} _ {b} x = — \ log _ {b} x = \ log _ {b} {\ frac {1} {x}}}

Свойства логарифмов

• Вопросы занятия:
• · рассмотреть свойства логарифмов;
• ·  подробно рассмотреть примеры, в которых необходимо преобразовать выражения с логарифмами.
• Материал урока
• Прежде чем приступить к изучению новой темы, давайте повторим определение логарифма, основное логарифмическое тождество:

Эти знания нам пригодятся на сегодняшнем уроке.

Сегодня мы рассмотрим основные свойства операции логарифмирования. Заметим, что все свойства мы будем формулировать только для положительных значений переменных, содержащихся под знаком логарифма.

1. Итак, первое свойство формулируется следующей теоремой:
2. Теорема 1.
3. Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел, то есть справедлива следующая формула:

Давайте докажем эту теорему.

Введём следующие обозначения.

Нам надо доказать, что выполняется равенство:

Применим определение логарифма.

По свойству произведения степеней с одинаковыми основаниями получим:

Поскольку степени двух положительных чисел равны и основания степеней равны и отличны от единицы, то равны и показатели степеней. Значит:

Что и требовалось доказать.

Рассмотрим пример.

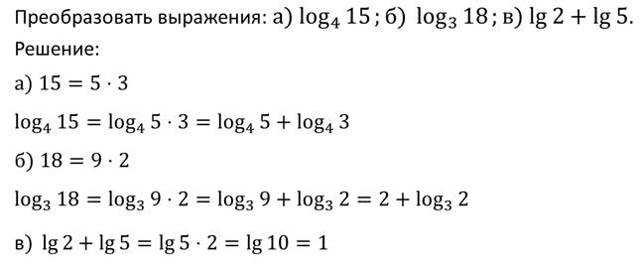
• Сформулируем следующее свойство логарифмов.
• Теорема 2.
• Если а, b, c – положительные числа, причём a ≠ 1, то справедливо равенство:

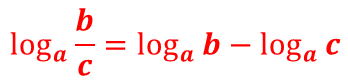
Другими словами, логарифм частного равен разности логарифмов делимого и делителя.

Или: логарифм дроби равен разности логарифмов числителя и знаменателя.

Эта теорема доказывается аналогично предыдущей. Поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.

1. Рассмотрим пример.
2. Сформулируем следующее свойство.
3. Теорема 3.
4. Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:
5. Другими словами, логарифм степени равен произведению показателя степени на логарифм основания степени.
6. Эта теорема доказывается аналогично предыдущим, поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.
7. Рассмотрим пример.
8. Сформулируем следующее свойство.
9. Свойство.
10. Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:
11. Другими словами: логарифм, основанием которого является степень числа а равен произведению единицы делённой на показатель степени и логарифма числа b по основанию а.
12. Эта теорема доказывается аналогично предыдущим, поэтому доказывать её мы не будем.
13. Рассмотрим пример.
14. Рассмотрим ещё один пример.

То есть нам удалось логарифм достаточно громоздкого выражения представить в виде суммы и разности логарифмов простых выражений. Такое преобразование называют логарифмированием.

Иногда приходиться решать обратную задачу: находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое действие называется потенцированием.

При этом используют следующее утверждение:

• Теорема 4.
• Равенство:
• справедливо тогда и только тогда, когда
• Это утверждение следует из монотонности логарифмической функции.
• Рассмотрим пример.

Ещё раз обратите внимание, что все свойства логарифмов мы получили при условии, что переменные принимают положительные значения. А как быть, если про знак переменной ничего неизвестно?

1. Например, можно ли записать:
2. Нет, нельзя, поскольку:
3. Правильнее будет записать так:
4. Мы должны помнить и о том, что:
5. только в том случае, когда b > 0 и с > 0. Если мы в этом не уверены, но знаем, что произведение bc > 0, то, поскольку в этом случае выполняется равенство:
6. то следует использовать формулу:
7. Рассмотрим ещё несколько примеров.
8. Пример.
9. Пример.
10. Пример.
11. Пример.
12. Итак, повторим основные свойства логарифмов:

таблица-шпаргалка свойств, формулы, примеры, график

Логарифм числа – это показатель степени, в которую нужно возвести одно число, чтобы получить другое.

Если число b в степени y равняется x:

by = x

Значит логарифм числа x по основанию b равен y:

y = log_b(x)

Например:

24 = 16

log₂(16) = 4

Логарифм как обратная функция к показательной

Логарифмическая функция y = log

b(x) является обратной функцией к показательной x=b y.

Так что, если мы вычислим показательную функцию логарифма х (х > 0), получится:f (f -1(x)) = blogb(x) = x

Или если мы вычислим логарифм показательной функции х:f -1(f (x)) = log_b(bx) = x

Натуральный логарифм (ln)

Натуральный логарифм – это логарифм по основанию е.

ln(x) = log_e(x)

Число e – это константа, которая может определяться как предел:

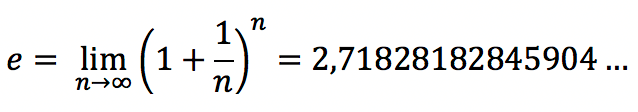
или так:

Обратный логарифм

Обратный логарифм (или антилогарифм) числа n – это число, логарифм которого по основанию a равен числу n.

ant log_an = an

Таблица свойств логарифмов

Ниже представлены основные свойства логарифмов в табличном виде.

Свойство
Формула
Пример
Основное логарифмическое тождество

a log_a b = b
2log₂8 = 8
Логарифм произведения

log_b (x ⋅ y) = log_b x + log_b y

log₁₀(3 ⋅ 7) = log₁₀3 + log₁₀7
Логарифм деления/частного
log_b (x / y) = log_b x — log_b y

log₁₀(37) = log₁₀3 — log₁₀7
Логарифм степени

log_b (x y) = y ⋅ log_b x

log₁₀(28) = 8 ⋅ log₁₀2

Логарифм числа по основанию в степени

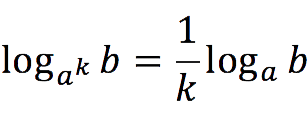
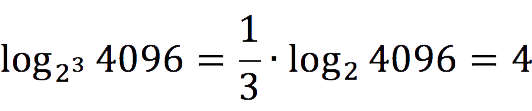
Логарифм корня

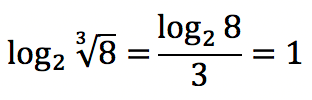
Перестановка основания логарифма
log_b c = 1 / log_c b

log₂8 = 1 / log₈2
Переход к новому основанию
log_b x = log_c x / log_c b

log₂8 = log₁₀8 / log₁₀2
Производная логарифма

f(x) = log_b x ⇒f ‘(x) = 1 / (x ⋅ ln b)

Интеграл логарифма
∫ log_b (x) dx = x ⋅ (log_b x — 1 / ln b) + C

Логарифм отрицательного числа
log_b x не определен, при x≤0

Логарифм числа 0
log_b 0 не определен

Логарифм числа 1
log_b 1 = 0, b>0, b≠0

log₂1 = 0
Логарифм числа, равного основанию
log_b b = 1, b>0, b≠0

log₂2 = 1
Логарифм бесконечности
lim log_b x = ∞, при x →∞

microexcel.ru