Уравнение прямой проходящей через две заданные точки
Что нужно сделать, если мы хотим найти уравнение прямой, проходящей через две точки (-1, 2) и (2, 4)?
Здесь мы не знаем коэффициент прямой, поэтому кажется, что мы не можем использовать ни одну из формул, которые мы знаем на данный момент. Но мы знаем две точки на прямой, и поэтому можем использовать их для определения коэффициента.
Следует просто использовать формулу \.
Получаем: \.
Таким образом, коэффициент прямой равен \.
Нам известны две точки на прямой, поэтому мы можем использовать одну из них в формуле y — y1 = m(x — x1). Если мы возьмем точку (2, 4), то получим:
y — 4 = \(x — 2)
3y — 12 = 2x — 4
3y = 2x + 8
\
Как и в предыдущих случаях, будет полезно найти общую формулу, которую можно использовать для примеров такого рода.
Итак, предположим, что общая прямая проходит через две точки \. Пусть общая точка на прямой будет P(x, y).
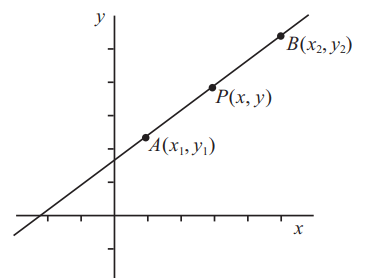
Теперь мы знаем, что коэффициент AP должен быть таким же, как коэффициент AB, так как все три точки лежат на одной прямой. Но коэффициент AP равен:
\
тогда как коэффициент AB равен:
\
Тогда mAP = mAB, поэтому мы имеем:
\
Эта формула довольно сложна, но ее легче запомнить, если все члены с участием y находятся на одной стороне, а все члены с участием x — на другой. Если мы будем преобразовывать эту формулу, сначала мы сможем получить:
\
а затем
\
Запомнить эту формулу вам поможет замечание, что закономерность в левой части, с участием y, такая же, как и с участием x в правой части.
Важно
Уравнение прямой, проходящей через две точки (x1, y1) и (x2, y2), имеет вид:
Теперь мы можем использовать эту формулу для решения примеров. Предположим, что мы хотим найти уравнение прямой, проходящей через две точки (1, -2) и (-3, 0).
Попробуем подставить в формулу и решить:
\
\
\
\
-2y — 4 = x — 1
-2y = x + 3
\
Таким образом, прямая имеет коэффициент — \, а значение и точку пересечения с осью \.
Мы также можем преобразовать уравнение, чтобы получить 2y = -x — 3, или 2y + x + 3 = 0.
Упражнение 2
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) проходящей через (4, 6) и (8, 26),
(2) проходящей через (1, 1) и (4, -8),
(3) проходящий через (3, 4) и (5, 4),
(4) проходящий через (0, 2) и (4, 0),
(5) проходящий через (-2, 3) и (2, -5).
От теории к практике
Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.
Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.
Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:
//**********************************************************
// Посчитать угол пересечения векторов по коэфф-ам А и B
//**********************************************************
function CalcCrossAngle(const a1,b1: Extended;
const a2,b2: Extended): Extended;
var
c1, c2: Extended;
begin
c1 := ArcTan2(a1,b1);
c2 := ArcTan2(a2,b2);
Result := c2-c1;
if Result < -pi then
Result := 2*pi + Result;
if Result > pi then
Result := Result — 2*pi;
end;
|
1 |
//********************************************************** functionCalcCrossAngle(consta1,b1Extended; consta2,b2Extended)Extended; var c1,c2Extended; begin c1=ArcTan2(a1,b1); c2=ArcTan2(a2,b2); Result=c2-c1; ifResult<-pithen Result=2*pi+Result; ifResult>pithen Result=Result-2*pi; end;
|
Тут ситуация с вертикальной прямой, т.е. когда теоретически происходит деление на ноль, явно не обрабатывается. Она корректно обрабатывается функцией ArcTan2, которая вернет в этом случае и знак, и 90 градусов.
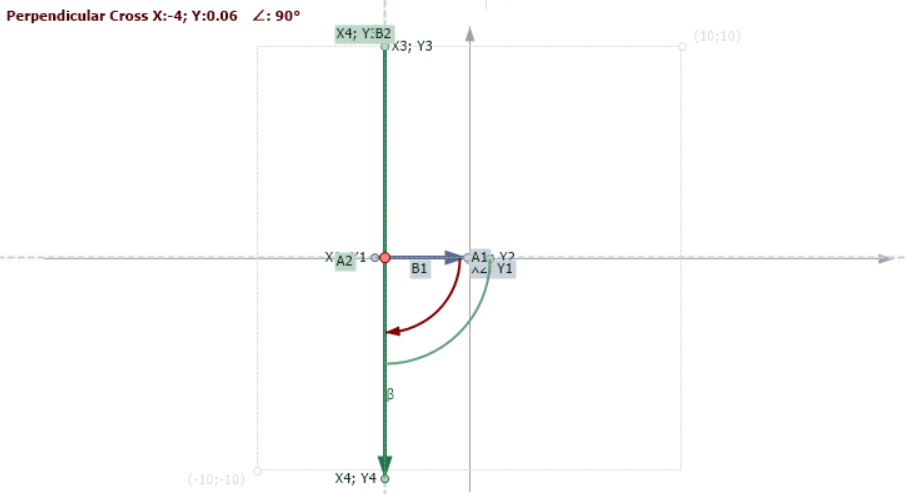Рис.7. Пересечение перпендикулярных векторов
Мой способ
Задача
Даны координаты двух отрезков. Нужно узнать, пересекаются ли отрезки, и если да, в какой точке. Для этой цели напишем функцию.
Решение
Условные обозначения для исключения недопониманий: a — вектор a, a(y) — проекция вектора a на ось Y, a — вектор a, заданный координатами x1,y1.
Представим наши отрезки в виде двух векторов: a и b
Обратите, внимание, что вектор b имеет противоположное от ожидаемого направление. Введём вектор c
Заметим, что a*k+b*n=c, где k,n — некоторые коэффициенты. Таким образом, получаем систему уравнений:
a(x)*k+b(x)*n=c(x) a(y)*k+b(y)*n=c(y) Наша задача сводится к нахождению этих коэффициентов (правда сказать, достаточно найти лишь один из них).
Предлагаю домножить обе части нижнего уравнения на q= -a(x)/a(y). Так после сложения двух уравнений, мы сразу избавимся от k. Нахождение n сведётся к решению обыкновенного линейного уравнения
Важно обратить внимание, что у n может не быть решения
Внимательный читатель заметит, что при a(y)=0, мы получим ошибку. Пропишем ветвление на этапе нахождения a(y). Этот случай ещё проще, ведь мы сразу получаем уравнение с одной неизвестной.
Рекомендую попробовать вывести n самостоятельно, так будет понятнее, что откуда берётся в коде ниже.
Зная n, можно найти точку пересечения, для этого мы отнимем от координаты точки (x3,y3) вектор b*n
Собираем воедино
Данная функция принимает координаты вершин и возвращает значение 1, если прямые отрезков (именно прямые) пересекаются, иначе 0. Если же вам нужны координаты вершин, вы сможете взять их из массива dot[].
Важно: при введении двух совпадающих прямых, алгоритм выводит отсутствие пересечения. Алгоритм находит точку пересечения прямых, на которых лежат отрезки, поэтому точка может оказаться за пределами отрезка (что вам придётся дополнительно проверить в уже своём коде)
Принадлежность точки отрезку
В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:
- Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
- Проверить факт нахождения точки между концами отрезка.
Займемся пунктом 2. Данный факт можно установить двумя способами:
- Логически, т.е. (x1 <= x <= x2) ИЛИ (x1 >= x >= x2
(y1 = y >= y2).
). На случай «вертикальности» линии добавить проверку на Y:
- Арифметически. Сумма отрезков |x-x1| + |x-x2| должна быть равна длине отрезка |x1-x2
|y-y1| + |y-y2| = |y1-y2|
|. Аналогично, на случай «вертикальности» , добавить проверку:
//*****************************************************
// Проверка факта нахождения точки res между
// концами отрезка (p1,p2).
// Решение с помощью условных операторов и
// коэффициентов A=(y2-y1) B=(x1-x2).
// Выступают в качестве параметров, чтобы не тратить
// время на их подсчет, т.к. в вызывающей стороне
// они уже посчитаны
//*****************************************************
function CheckCrossPoint(const p1, p2, res: TxPoint;
const A,B: Extended): Boolean;
begin
Result :=
(((B<0) and (p1.X < res.X) and (p2.X > res.X)) or
((B>0) and (p1.X > res.X) and (p2.X < res.X)) or
((A<0) and (p1.y > res.Y) and (p2.Y < res.Y)) or
((A>0) and (p1.y < res.Y) and (p2.Y > res.Y)));
end;
//*****************************************************
// Проверить факт нахождения точки res между
// концами отрезка (p1,p2)
// Арифметическое решение без коэффициентов
//*****************************************************
function CheckCrossPoint(const p1, p2, res: TxPoint): Boolean;
begin
Result :=
(abs(p2.x-p1.x)>= abs(p2.x-res.x) + abs(p1.x-res.x)) and
(abs(p2.y-p1.y)>= abs(p2.y-res.y) + abs(p1.y-res.y));
end;
|
1 |
//***************************************************** functionCheckCrossPoint(constp1,p2,resTxPoint; constA,BExtended)Boolean; begin Result= (((B<)and(p1.X<res.X)and(p2.X>res.X))or ((B>)and(p1.X>res.X)and(p2.X<res.X))or ((A<)and(p1.y>res.Y)and(p2.Y<res.Y))or ((A>)and(p1.y<res.Y)and(p2.Y>res.Y))); end; functionCheckCrossPoint(constp1,p2,resTxPoint)Boolean; begin Result= (abs(p2.x-p1.x)>=abs(p2.x-res.x)+abs(p1.x-res.x))and (abs(p2.y-p1.y)>=abs(p2.y-res.y)+abs(p1.y-res.y)); end;
|
Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.
Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.
Совет 1: Как найти координаты точки пересечения двух прямых
Напишем еще три новые функции.
Функция LinesCross() будет определять, пересекаются
ли два отрезка
. В ней взаимное расположение отрезков определяется с помощью векторных произведений. Для вычисления векторных произведений напишем функцию – VektorMulti().
Функция RealLess() будет использоваться для реализации операции сравнения “
Задача1. Два отрезка заданы своими координатами. Составить программу, которая определяет, пересекаются ли эти отрезки
, не находя точку пересечения.
Решение. Второй задан точками .
Рассмотрим отрезок и точки и .
Точка лежит слева от прямой , для нее векторное произведение > 0, так как векторы положительно ориентированы.
Точка расположена справа от прямой, для нее векторное произведение
Для того чтобы точки и , лежали по разные стороны от прямой , достаточно, чтобы выполнялось условие
Аналогичные рассуждения можно провести для отрезка и точек и .
Итак, если , то отрезки пересекаются.
Для проверки этого условия используется функцию LinesCross(), а для вычисления векторных произведений – функция VektorMulti().
ax, ay – координаты первого вектора,
bx, by – координаты второго вектора.
Program geometr4; {Пересекаются ли 2 отрезка?} Const _Eps: Real=1e-4; {точность вычслений} var x1,y1,x2,y2,x3,y3,x4,y4: real; var v1,v2,v3,v4: real;function RealLess(Const a, b: Real): Boolean; {Строго меньше} begin RealLess:= b-a> _Eps end; {RealLess}function VektorMulti(ax,ay,bx,by:real): real; {ax,ay — координаты a bx,by — координаты b } begin vektormulti:= ax*by-bx*ay; end;Function LinesCross(x1,y1,x2,y2,x3,y3,x4,y4:real): boolean; {Пересекаются ли отрезки?} begin v1:=vektormulti(x4-x3,y4-y3,x1-x3,y1-y3); v2:=vektormulti(x4-x3,y4-y3,x2-x3,y2-y3); v3:=vektormulti(x2-x1,y2-y1,x3-x1,y3-y1); v4:=vektormulti(x2-x1,y2-y1,x4-x1,y4-y1); if RealLess(v1*v2,0) and RealLess(v3*v4,0) {v1v2
Результаты выполнения программы:
Введите координаты отрезков: -1 1 2 2.52 2 1 -1 3 Да.
Мы написали программу, определяющую, пересекаются ли отрезки, заданные своими координатами.
На следующем уроке мы составим алгоритм, с помощью которого можно будет определить, лежит ли точка внутри треугольника.
Уважаемый читатель.
Вы уже познакомились с несколькими уроками из серии «Геометрические алгоритмы». Все ли доступно написано? Я буду Вам очень признательна, если Вы оставите отзыв об этих уроках. Возможно, что-то нужно еще доработать.
Пусть даны два отрезка. Первый задан точками P 1 (x 1 ;y 1)
и P 2 (x 2 ;y 2)
. Второй задан точками P 3 (x 3 ;y 3)
и P 4 (x 4 ;y 4)
.
Взаимное расположение отрезков можно проверить с помощью векторных произведений:
Рассмотрим отрезок P 3 P 4
и точки P 1
и P 2
.
Точка P 1
лежит слева от прямой P 3 P 4
, для нее векторное произведение v 1 > 0
, так как векторы положительно ориентированы. Точка P 2
расположена справа от прямой, для нее векторное произведение v 2 , так как векторы отрицательно ориентированы.
Для того чтобы точки P 1
и P 2
лежали по разные стороны от прямой P 3 P 4
, достаточно, чтобы выполнялось условие v 1 v 2 (векторные произведения имели противоположные знаки).
Аналогичные рассуждения можно провести для отрезка P 1 P 2
и точек P 3
и P 4
.
Итак, если v 1 v 2 и v 3 v 4 , то отрезки пересекаются.
Векторное произведение двух векторов вычисляется по формуле: где:ax
, ay
— координаты первого вектора,bx
, by
— координаты второго вектора.
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
Пусть на прямой заданы две не совпадающие точки:P 1
с координатами (x 1 ;y 1)
и P 2
с координатами (x 2 ; y 2)
.
Угол пересечения прямых
Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p1 и p2, получим направляющий вектор V(p1,p2), и аналогично второй вектор M(p3,p4). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.
Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:
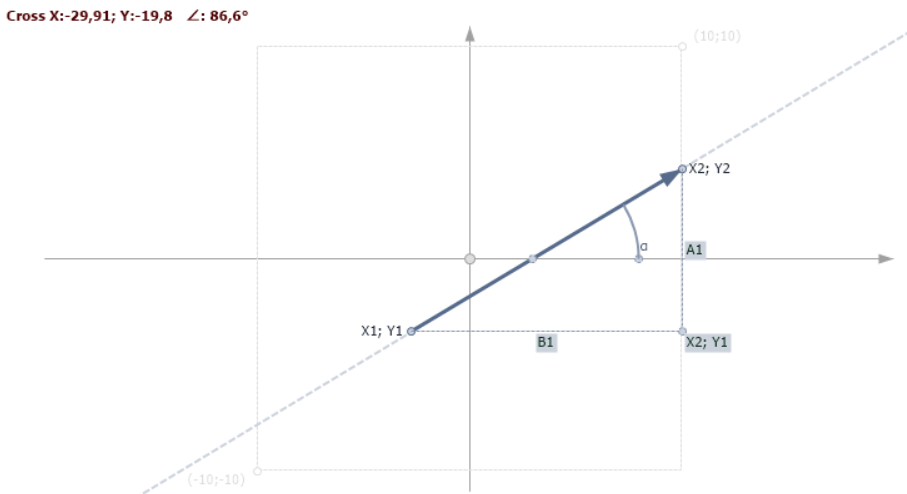
Рис.4. Вектор V(p1,p2)
α — угол наклона вектора к оси X, который можно найти, как:
α = arctan (A1 / B1)
Где расстояния:
A1 = (y1 — y2)
B1 = (x2 — x1)
Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…
Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.
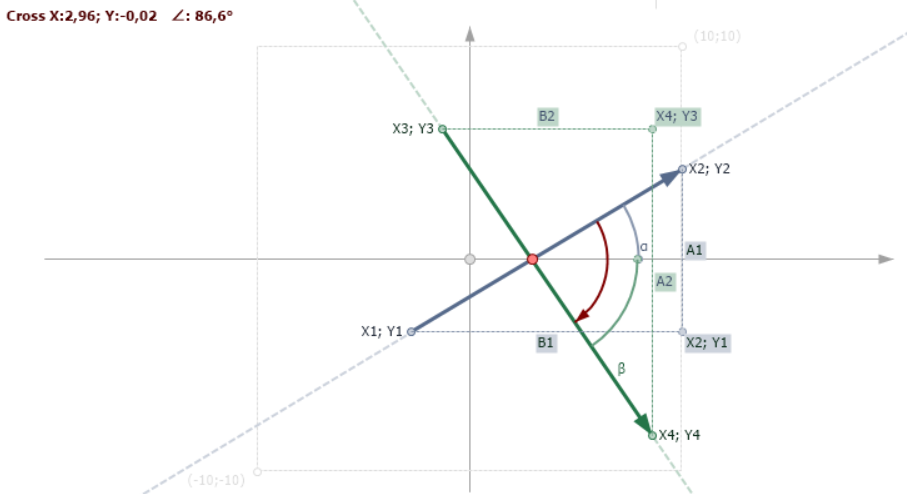
Рис.5. Пересекающиеся вектор V(p1,p2) и вектор M(p3,p4)
Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.
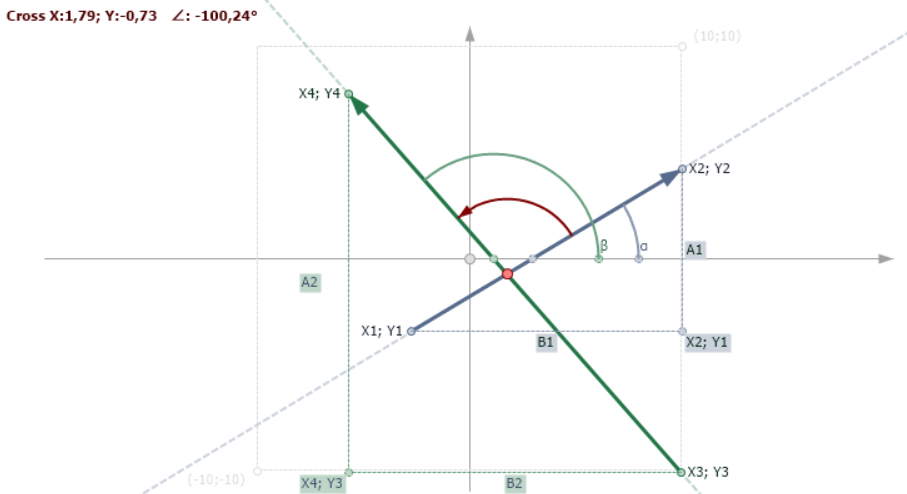
Рис.6. Пересекающиеся векторы в положительной Y
По рисунку явно видно, что угол между векторам это γ = (β — α).
В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.
Уравнение в программный код
На бумаге всё славненько, надо также сделать и в программном коде. Но программы не разбираются в уравнениях, им подавай переменные, постоянные и функции. Программный код не терпит неопределенности, он требует точные данные. Очень желательно строить выражения без операций деления. Преобразуем в программный код уравнение с коэффициентами (у.3) описанное выше. Для каждой прямой своё уравнение и переменные.
Точки определяющие прямые запишем в структуры Point. У каждой прямой две точки и они являются входными данными: Определяем коэффициенты и свободные члены уравнений. Записываем их в соответствующие переменные: Точка пересечения также будет храниться в структуре Point:
Популярные способы и их критика
Возможно, многие вспомнят способ из школьной алгебры — составить уравнения двух прямых, приравнять их правые части, найти x, и подставить его в уравнение прямой, чтобы найти y (Подробнее здесь).
Однако данный способ становится достаточно громоздким при написании кода (возможно поэтому вы сейчас читаете эту статью), к тому же, он не является универсальным: если одна из прямых параллельна оси Y, мы получим ошибку деления на ноль при вычислении углового коэффициента, и нам придётся прописать код на этот случай; если две прямые перпендикулярны осям, требуется повозиться с обработкой и этого случая. Такой код становится длинным и некрасивым.
В поисках более элегантного решения данной проблемы я наткнулся на весьма интересные способы, основанные на векторном умножении ( habr.com/ru/post/267037 ) и ray castinging’е ( ru.wikipedia.org/wiki/Ray_casting#Концепция ). Но на мой взгляд, они неоправданно сложные в вычислительном плане. Поэтому представляю вашему вниманию (и критике) мой способ.
Практика 2
В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.
//**********************************************************
// Тип пересечения прямых (p1,p2) и (p3,p4)
//**********************************************************
type
TxCrossLineResult = (
xclrEqual = -32// эквивалентны
,xclrParallel = -16// параллельны
,xclrOk = 0 // как минимум пересечение есть
,xclrFirst = 1 // попадает в первый отрезок
,xclrSecond = 2 // попадает во второй отрезок
,xclrBoth = 3 // попадает в оба
,xclrPerpend = 4 // перпендикулярны
// можно найти по маске через AND, но для полноты картины
,xclrFirstP = 5 // перпендикулярны и попадает в первый
,xclrSecondP = 6 // перпендикулярны и попадает в второй
,xclrBothP = 7 // перпендикулярны и попадает в оба
);
//**********************************************************
// Нахождение точки пересечения прямых (p1,p2) и (p3,p4)
// Определяет параллельность, совпадение,
// перпендикулярность, пересечение.
// Определяет, каким отрезкам принадлежит.
// Находит угол(рад.) от (p1,p2) к (p3,p4):
// отрицательное значение — против часовой
// положительное — по часовой
//**********************************************************
function CrossLines(const p1,p2,p3,p4: TxPoint;
var res: TxPoint; var Angle: Extended): TxCrossLineResult;
const
Prec = 0.0001;
var
a1, a2: Extended;
b1, b2: Extended;
c1, c2: Extended;
v: Extended;
begin
Angle := 0;
a1 := p2.y — p1.y;
a2 := p4.y — p3.y;
b1 := p1.x — p2.x;
b2 := p3.x — p4.x;
c1 := p2.x*p1.y — p1.x*p2.y;
c2 := p4.x*p3.y — p3.x*p4.y;
v := a1*b2 — a2*b1;
if abs(v) > Prec then
begin
Result := xclrOk;
res.X := -(c1*b2 — c2*b1)/v;
res.Y := -(a1*c2 — a2*c1)/v;
if CheckCrossPoint(p1,p2,res) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrFirst));
if CheckCrossPoint(p3,p4,res) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrSecond));
if (abs(a1*a2 + b1*b2) < Prec) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrPerpend));
Angle := CalcCrossAngle(a1,b1,a2,b2);
end else
begin
Result := xclrParallel;
if ((abs(c1*b2 — c2*b1) < Prec) and
(abs(a1*c2 — a2*c1) < Prec))
then
Result := xclrEqual;
end;
end;
|
1 |
//********************************************************** TxCrossLineResult=( xclrEqual=-32// эквивалентны ,xclrParallel=-16// параллельны ,xclrOk=// как минимум пересечение есть ,xclrFirst=1// попадает в первый отрезок ,xclrSecond=2// попадает во второй отрезок ,xclrBoth=3// попадает в оба ,xclrPerpend=4// перпендикулярны // можно найти по маске через AND, но для полноты картины ,xclrFirstP=5// перпендикулярны и попадает в первый ,xclrSecondP=6// перпендикулярны и попадает в второй ,xclrBothP=7// перпендикулярны и попадает в оба ); functionCrossLines(constp1,p2,p3,p4TxPoint; varresTxPoint;varAngleExtended)TxCrossLineResult; const Prec=0.0001; var a1,a2Extended; b1,b2Extended; c1,c2Extended; vExtended; begin Angle=; a1=p2.y-p1.y; a2=p4.y-p3.y; b1=p1.x-p2.x; b2=p3.x-p4.x; c1=p2.x*p1.y-p1.x*p2.y; c2=p4.x*p3.y-p3.x*p4.y; v=a1*b2-a2*b1; ifabs(v)>Prec then begin Result=xclrOk; res.X=-(c1*b2-c2*b1)/v; res.Y=-(a1*c2-a2*c1)/v; ifCheckCrossPoint(p1,p2,res)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrFirst)); ifCheckCrossPoint(p3,p4,res)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrSecond)); if(abs(a1*a2+b1*b2)<Prec)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrPerpend)); Angle=CalcCrossAngle(a1,b1,a2,b2); endelse begin Result=xclrParallel; if((abs(c1*b2-c2*b1)<Prec)and (abs(a1*c2-a2*c1)<Prec)) then Result=xclrEqual; end; end;
|
геометрия — Расчет координат точки пересечения высоты и основания треугольника
$\begingroup$
Для любого треугольника $\Delta ABC$ каковы координаты точки $D$ вдоль прямой $\overline{BC}$, такой, что $\overline{AD}$ перпендикулярна $\overline{BC} $?
Например, дан треугольник $\Delta ABC$, где $(A_x = -1,\ A_y = 4)$, $(B_x = -1,\ B_y = 2)$ и $(C_x = 5, \ C_y = 1)$, решение $(D_x = 1,4,\ D_y = -0,8)$. Я знаю решение этого конкретного примера из этого видео, объясняющего, как вычислять высоты. Это был один из примеров, использованных в видео, но он был рассчитан с использованием многоэтапного процесса.
Я знаю, что наклон отрезка $\overline{BC}$ является отрицательной обратной величиной $m_\overline{BC}$.
$$m_\overline{BC} = \frac{y_2 — y_1}{x_2 — x_1}$$
$$m_\overline{BC} = \frac{1 — (-2)}{5 — (-1)}$$
$$m_\overline{BC} = \frac{1}{2}$$
$$m_\overline{AD} = \frac{-1}{\frac{1}{2}}$$
$$m_\overline{AD} = -2$$
Несмотря на то, что я могу рассчитать наклон линии, я не уверен, в какой точке она пересечет $\overline{BC}$.
Я ищу общую формулу для вычисления декартовых координат $x$ и $y$ точки $D$. Предоставьте явное решение для координат $x$ и $y$ точки $D$, обозначенных как $D_x$ и $D_y$ соответственно.
- геометрия
- тригонометрия
- треугольники
$\endgroup$
7
$\begingroup$
Вот пошаговый подход.
$1.$ Поскольку у нас есть координаты $B$ и $C$, мы можем вычислить вектор нормали единиц к отрезку $BC$. Вот как вы можете это сделать
$$\begin{align}
{\bf{L}}&= {\bf{x}}_B-{\bf{x}}_C\\
&=(x_B-x_C){\bf{i}}+(y_B-y_C){\bf{j}} \\
\\
{\bf{N}}&= {\bf{k}} \times {\bf{L}}\\
&=-(y_B-y_C){\bf{i}}+(x_B-x_C){\bf{j}} \\
\\
{\bf{N}} \cdot {\bf{L}} &= 0 \\
\\
{\bf{n}} &= \frac{\bf{N}}{\|\bf{N}\|} \\
&= \frac{{\bf{k}} \times {\bf{L}}}{\|\bf{L}\|} \\
&= \frac{{\bf{k}} \times ({\bf{x}}_B-{\bf{x}}_C)}{\|{\bf{x}}_B-{\bf{ х}}_С\|}\\
& = \ frac {- (y_B-y_C) {\ bf {i}} + (x_B-x_C) {\ bf {j}}} {\ sqrt {(x_B-x_C) ^ 2+ (y_B-y_C) ^ 2}}
\end{выравнивание}$$
$2.
$$d = ({\bf{x}}_B-{\bf{x}}_A)\cdot{\bf{n}}$$
, поэтому мы нашли длину $AD$.
$3.$ Координаты $D$ будут
$$\begin{align}
{\bf{x}}_D &= {\bf{x}}_A + d{\bf{n}} \\
&= {\bf{x}}_A + {\bf{n}} \\
\\
&= {\bf{x}}_A + \left\frac{{\bf{ k}} \times ({\bf{x}}_B-{\bf{x}}_C)}{\|{\bf{x}}_B-{\bf{x}}_C\|} \\
\end{выравнивание}$$ 92} (х_В-х_С)
\end{выравнивание}
}$$
Кроме того, вот файл MAPLE, который может помочь читателю этого сообщения для вычисления окончательных формул, упомянутых здесь, и проверки примера, упомянутого в вопросе.
$\endgroup$
1
$\begingroup$
Пусть $A:(x_1,y_1)$, $B:(x_2,y_2)$, $C:(x_3,y_3)$.
Таким образом, уравнение прямой через $BC$ будет таким: $$y-y_2=(\frac{y_2-y_3}{x_2-x_3})(x-x_2)$$
Таким образом, наклон высоты будет отрицательным обратным,
$$-\влево(\frac{x_2-x_3}{y_2-y_3}\вправо)$$
Итак, уравнение прямой:
$$y=c-\left(\frac{x_2-x_3}{y_2-y_3}\right)x$$
Ввод значений и решение для $ c $ дает уравнение,
$$y=y_1+\left(\frac{x_2-x_3}{y_2-y_3}\right)x_1-\left(\frac{x_2-x_3}{y_2-y_3}\right)x$$
Теперь просто решите два уравнения одновременно.
Второй способ
Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.
Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.
Решение:
Второе уравнение проще первого, поэтому подставим его вместо $y$:
Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:
$y_1= 2 + 1 = 3; y_2=1 — \frac = \frac$.
Точки пересечения будут $(2;3)$ и $(-\frac; \frac)$.
Другие перекрестки
Перекрестки не ограничиваются двумя линиями. Мы можем вычислить точку пересечения между всеми типами кривых. Если мы посмотрим дальше, чем только линии, мы можем получить ситуации, в которых есть более одного пересечения. Есть даже примеры комбинаций функций, имеющих бесконечно много пересечений. Например, прямая y = 1 (поэтому y = ax + b, где a = 0 и b = 2) имеет бесконечное количество пересечений с y = cos (x), поскольку эта функция колеблется между -1 и 1.
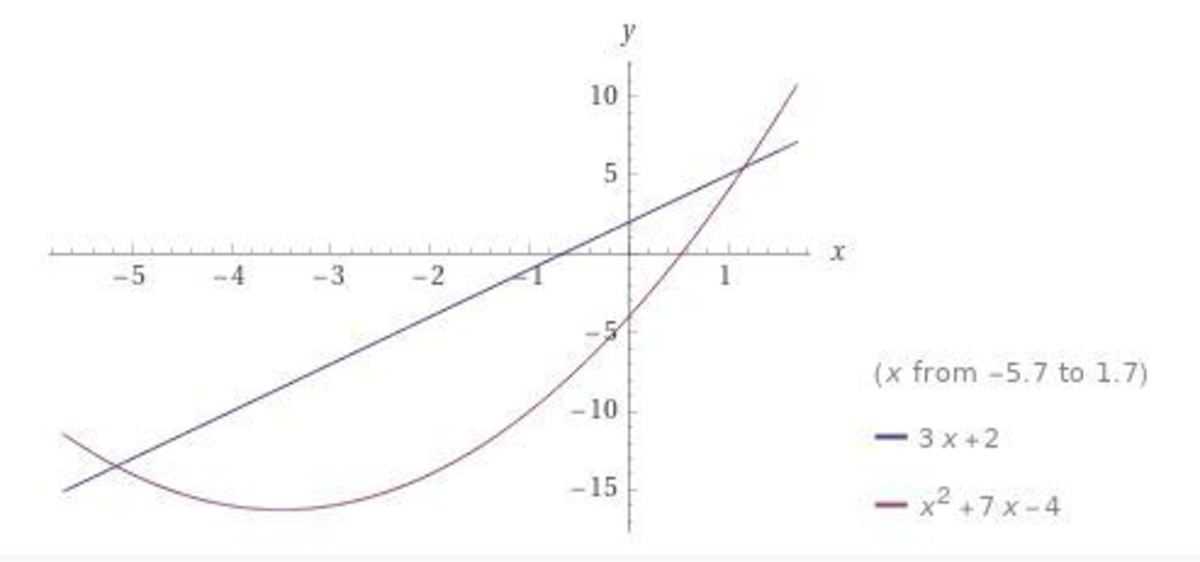
Здесь мы рассмотрим пример пересечения линии и параболы. Парабола — это кривая, которая представлена выражением y = ax 2 + bx + c. Метод нахождения перекрестка остается примерно таким же. Давайте, например, посмотрим на пересечение двух следующих кривых:
у = 3х + 2
у = х 2 + 7х — 4
Мы снова приравниваем два выражения и смотрим на 3x + 2 = x 2 + 7x — 4.
Мы перепишем это в квадратное уравнение так, чтобы одна сторона знака равенства была равна нулю. Затем мы должны найти корни полученной квадратичной функции.
Итак, начнем с вычитания 3x + 2 по обе стороны от знака равенства:
0 = х 2 + 4х — 6
х 2 + 4х — 6 = 0
(х + 2) 2 -10 = 0
(х + 2) 2 = 10
Тогда решения следующие: x = -2 + sqrt 10 и x = -2 — sqrt 10.
Теперь заполним это решение в обоих выражениях, чтобы проверить, правильно ли оно.
y = 3 * (- 2 + sqrt 10) + 2 = — 4 + 3 * sqrt 10
y = (-2 + sqrt 10) 2 + 7 * (- 2 + sqrt 10) — 4 = 14-4 * sqrt 10-14 + 7 * sqrt 20-4
= — 4 + 3 * sqrt 10
Так что действительно, эта точка была точкой пересечения. Можно проверить и другой момент. Это приведет к точке (-2 — sqrt 10, -4 — 3 * sqrt 10)
Важно убедиться, что вы выбрали правильные комбинации, если существует несколько решений
Всегда полезно нарисовать две кривые, чтобы увидеть, имеет ли смысл то, что вы рассчитали. На картинке ниже вы видите две точки пересечения.
Математика: как найти корни квадратичной функции
