Натуральный логарифм и число е

История числа “е”

История числа «е» (экспонента) начинается с работ по различным математическим проблемам, связанным с ростом и изменением величин.

Первоначальные следы идеи числа «е» можно найти в древнегреческой математике. Архимед, живший в 3 веке до н.э., использовал концепцию непрерывно растущей величины в своей работе по арифметике и аппроксимации. Однако само число «е» не было определено или формально выражено в то время.

Понятие числа «е» стало более явным в 17 веке благодаря работам различных математиков. Важную роль сыграли математики Йоханнес Непер (Neper) и Леонард Эйлер (Euler).

Йоханнес Непер, шотландский математик, известен своими исследованиями логарифмов и экспоненты. В 1614 году он ввел понятие «натурального логарифма» и опубликовал таблицу логарифмов, в которой основание было примерно равно 2,71828. Неперу приписывается введение идеи числа «е» в связи с непрерывным ростом и сложными процентами.

Леонард Эйлер, швейцарский математик, сделал значительный вклад в развитие математики и внес большой вклад в изучение числа «е». В его работах он использовал ряд Тейлора для определения значения «е» и показал его связь с тригонометрическими функциями. Эйлер также ввел символ «е» для обозначения этой константы.

С течением времени понимание и значение числа «е» углублялись. В 19 веке были разработаны более точные методы вычисления числа «е» и были установлены его свойства, такие как иррациональность и возрастание функции экспоненты.

Сегодня число «е» является одной из фундаментальных математических констант, широко используется во многих областях науки, инженерии и финансов и играет важную роль в математических моделях и уравнениях.

Вопросы и ответы

Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.

Что такое число «е»?

Число «е» (экспонента или число Эйлера) является одной из фундаментальных математических констант. Оно приближенно равно 2,71828 и используется в различных математических моделях и уравнениях.

Как определить число «е»?

Число «е» может быть определено различными способами, включая представление через бесконечный ряд, такой как ряд Тейлора для экспоненты, где «е» равно сумме бесконечного числа слагаемых 1/n!, где n принимает значения от 0 до бесконечности.

Как число «е» связано с натуральным логарифмом?

Число «е» является основанием натурального логарифма. Натуральный логарифм любого положительного числа можно выразить через число «е». Например, ln(«е») = 1.

Как число «е» применяется в финансовых расчетах?

Число «е» используется в формулах, связанных с непрерывным сложным процентом в финансовых расчетах. Например, формула для расчета будущей стоимости непрерывного сложного процента выглядит следующим образом: FV = PV * e^(r*t), где FV — будущая стоимость, PV — текущая стоимость, r — процентная ставка и t — время.

Как число «е» связано с комплексными числами?

Число «е» связано с комплексными числами через формулу Эйлера: e^(ix) = cos(x) + i*sin(x), где «i» — мнимая единица, «x» — угол в радианах, а cos(x) и sin(x) — косинус и синус угла «x». Эта формула позволяет связать экспоненциальную функцию с тригонометрическими функциями.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор логарифмов. Вычислите онлайн натуральные, десятичные логарифмы (или с другим основанием) с решением.
• Возведение дроби в степень. Возведите онлайн любую дробь (десятичную и обыкноенную) в любую степень.
• Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
• Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
• Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
• Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
• На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
• На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.
• Тренажер таблицы умножения. Тренируйтесь и запоминайте таблицу умножения онлайн. Выберите нужный диапазон множителей, и система сгенерирует задания.

Характеристики

Иррациональность

Первое доказательство иррациональности в е связано с Эйлера ( ). Фурье дал следующее более простое доказательство, используя разложение е по экспоненциальному ряду и рассуждая из абсурда .

Это вопрос доказательства того, что для любого целого n > 0 число n e не является целым. Для этого он показывает, что само n ! E не является целым, разложив его в виде
нет!езнак равноИкс+y{\ Displaystyle п! \, \ mathrm {е} = х + у},
где числа x и y определяются как:
Иксзнак равнонет!∑kзнак равнонет1k!,yзнак равнонет!∑kзнак равнонет+1∞1k!{\ displaystyle x = n! \ sum _ {k = 0} ^ {n} {\ dfrac {1} {k!}}, \ qquad y = n! \ sum _ {k = n + 1} ^ {\ infty} {\ dfrac {1} {к!}}}.

• Число x является целым числом как сумма целых чисел n ( n — 1) ( n — 2)… ( k + 1) (для k от до n );
• Число y не целое. В самом деле, это строго между 0 и 1.

Таким образом, n ! E — это сумма целого и нецелого числа; следовательно, это не целое; a fortiori , н е не полный. Этот вывод верен независимо от целого числа n > 0 , поэтому e является иррациональным.

Непрерывная фракция

Еще одно доказательство иррациональности числа e — использование цепных дробей . Если доказательство более сложное, оно также предлагает больше возможностей для обобщения.

В 1737 году Эйлер получил разложение е в виде непрерывной дроби  :
езнак равно2+11+12+11+11+14+11+11+16+…{\ Displaystyle \ mathrm {e} = 2 + {\ frac {1} {1 + {\ frac {1} {2 + {\ frac {1} {1 + {\ frac {1} {1 + {\ frac) {1} {4 + {\ frac {1} {1 + {\ frac {1} {1 + {\ frac {1} {6+ \ ldots}}}}}}}}}}}}}}} }}}}.
Поскольку это развитие бесконечно, это число иррационально.

В 1761 году Ламберт расширил доказательство, данное Эйлером, и показал, используя разложения в обобщенные цепные дроби , что для любого ненулевого рационального r (в частности, для любого ненулевого целого) e r иррационально.

Этот подход также позволяет установить, что e не является квадратичным иррациональным , т. Е. Не является решением какого-либо квадратного уравнения с рациональными коэффициентами ( см. Непрерывная дробь и диофантово приближение ).

Тем не менее, мера иррациональности в е равно 2 , как и иррациональных алгебраических чисел , как указано по теореме Рота .

Превосходство

Чтобы пойти дальше, то есть, чтобы показать, что e не является решением какого-либо уравнения третьей степени с рациональными коэффициентами, затем, что оно трансцендентно , что означает, что оно не является решением d ‘никаких полиномиальных уравнений с рациональными коэффициентами, нужны новые идеи.

Трансцендентность e была установлена Чарльзом Эрмитом в 1873 году с помощью метода, предвосхищающего теорию аппроксимаций Паде , развитую в 1892 году в диссертации его ученика Анри Паде . Различные аппроксимации Паде экспоненциальной функции действительно дают много выражений e в форме обобщенных цепных дробей.

Поскольку e трансцендентен, то же самое и e r для любого ненулевого рационального r (и в более общем смысле: f ( e ) для любой непостоянной алгебраической функции f ).

Теорема Гельфонда-Шнайдера также позволяет продемонстрировать, что, например, e π трансцендентно, но в 2020 году мы еще не знаем, будут ли e e и π e трансцендентными или нет (однако предполагается, что все числа этой формы есть).

Также предполагается, что e — нормальное число .

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Экспонента

Для тех, кто не знает, экспонента — это функция:

И она, пожалуй, вызывает куда больший интерес, чем само число е. Хотя бы потому, что производная от этой функции равна самой этой функции.

А если еще вспомнить, что интегрирование — это обратный процесс к дифференцированию, не нужно иметь семь пядей во лбу, чтоб догадаться, что интеграл от e^x так же будет равен e^x.

Но не будем сильно углубляться в математику, а чтобы понять как этим всем пользоваться, ответим на несколько простых вопросов:

Что если мы вкладываем не один рубль, а два?

Число е показывает максимально возможное значение роста единичного вклада при непрерывной капитализации. То есть, если перевести на человеческий язык, с одного рубля при 100% годовых максимум за год набежит е рублей. Если изначальный вклад будет в двое больше, то максимум который мы можем получить через год тоже будет вдвое больше. 2е. Ну или 1000е если положить 1000 рублей.

— то что было.

— то что будет.

Что будет через 2-3 года?

Здесь тоже нет ничего сложного, эти 2-3 года уйдут в степень над числом (t — время).

Мы говорили, что набегает у нас с единичного вклада, соответственно, в начале следующего года у нас на счету уже рублей. Соответственно, вклад в начале второго года у нас уже не единичный. А как мы считаем рост, если вклад не единичный? Умножаем на величину этого вклада. То есть на . В конце второго года у нас на счету или рублей, через 3 года … И так далее.

Ну, а если мы имеем дело не со 100%, а скажем 10%?

Проценты в виде постоянной роста () также идут в степень. при 100% соответственно, при 10%.

Почему так происходит? Если не углубляться в математику, то можно сказать, что рост за год при 10% годовых будет такой же, как при 100% годовых за года. Ну а время у нас уходит в степень.

Все сказанное можно обобщить и представить в виде формулы:

Причем использовать эту формулу вы можете не только в области финансов. С ее помощью можно спрогнозировать рост населения в нашей необъятной Родине, рассчитать сколько радиоактивного радия останется в Вашем шкафу через год, если предварительно положить туда 10 грамм. Даже можно с легкостью определить когда от этого радия останется ровно половина.

Как на практике применяется число “е”?

Число «е» имеет множество практических применений в различных областях науки, инженерии и финансов. Вот несколько примеров его практического использования:

1. Финансовые расчеты. Число «е» используется в финансовых расчетах, связанных с непрерывным сложным процентом. Например, формула для расчета будущей стоимости непрерывного сложного процента выглядит следующим образом: FV = PV * e^(r*t), где FV — будущая стоимость, PV — текущая стоимость, r — процентная ставка и t — время.
2. Математическое моделирование. Число «е» встречается в различных математических моделях, используемых для описания роста и распространения в различных областях, таких как биология, экология, физика и т.д. Например, модель для описания экспоненциального роста может иметь вид: N(t) = N0 * e^(r*t), где N(t) — количество в момент времени t, N0 — начальное количество, r — коэффициент роста и t — время.
3. Компьютерная графика. Число «е» используется в алгоритмах компьютерной графики, таких как алгоритмы рендеринга и аппроксимации кривых. Например, для создания плавных анимаций или реалистичного освещения, число «е» может быть использовано для моделирования затухания или изменения яркости объектов.
4. Физика и инженерия. Число «е» встречается в различных физических и инженерных уравнениях. Например, в уравнении для расчета колебаний в электрической цепи или в уравнении для расчета времени зарядки или разрядки конденсатора.
5. Вероятность и статистика. Число «е» связано с понятием непрерывного распределения вероятностей, такого как нормальное распределение. Вероятностные модели, основанные на непрерывном распределении, используют число «е» для расчета вероятностей и оценки статистических характеристик.

Это только несколько примеров применения числа «е» на практике. Фактически число е присутствует во многих других областях, включая дифференциальные уравнения, теорию информации, сигнальную обработку, теорию управления и многие другие. Оно является одной из фундаментальных математических констант, которая обладает уникальными математическими свойствами и находит применение в различных контекстах.

Дополнение 2. Тригонометрическая форма и умножение комплексных чисел

$$\begin{tikzpicture}\small
\tikzset{>=stealth}
\def\r{2.3}
\def\l{4}
\def\ll{\l*0.8}
\def\h{0.6}
\def\a{2.4}
\def\b{1.8}
\def\t{0.07}
\def\p{0.5}
\draw(-\h,0)—(\l,0);
\draw(0,-\h)—(0,\ll);
\draw(0,0)—(\a,0) node {$a$};
\draw(\a,0)—(\a,\b) node {$b$};
\draw(0,0)—(\a,\b) node {$r$} node {$(a,b)$};
\draw(\p,0) arc (0:atan2(\b,\a):\p) node {$\alpha$};
\path(0,0) node {0};
\draw (-\h,-\h) rectangle (\l,\ll);
\end{tikzpicture}$$

После перехода от декартовых координат к полярным через последние можно выразить действительную и мнимую часть комплексного числа a + bi, которые являются катетами в треугольнике с гипотенузой r и углом α:

a = r cos α,     b = r sin α,     a + bi = r (cos α + i sin α).

Перемножим два комплексных числа в тригонометрической форме:

r (cos α + i sin α) · R (cos β + i sin β) = rR .

Вспоминая тригонометрические формулы, видим, что в круглых скобках получились выражения для косинуса и синуса суммы углов. Окончательный ответ имеет вид

r (cos α + i sin α) · R (cos β + i sin β) = rR .

Таким образом, модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргумент произведения есть сумма произведений сомножителей.

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

В следующий статье мы посмотрим на пример экспоненциального роста ваших денег.

Общие сведения

Формула Эйлера утверждает, что:

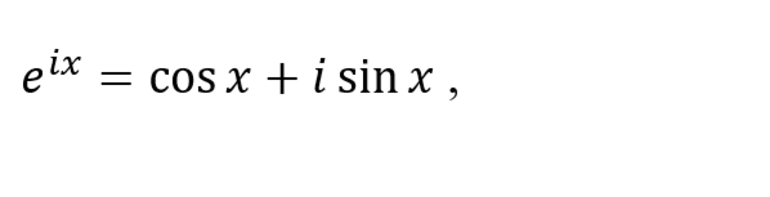
• i — мнимая единица, то есть корень квадратный из -1;
• e – экспонента, одна из важнейших математических констант, определяется выражением:

Формула, связывающая тригонометрические и функции экспоненциальные выражения, имеет множество применений. Она позволяет рассчитать некоторые выражения, решения которых невозможно или проблематично вычислить другим путём.

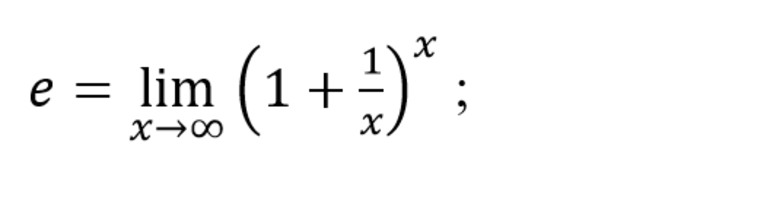
Необходимо лишь превратить исходные формулы в конструкцию, которая будет содержать удобные для проведения дальнейших операций функции.

История создания

Первым формулу опубликовал Роджер Котс, математик родом из Англии, в научном журнале, издаваемом Лондонским королевским обществом. Затем, формула была отображена в книге «Гармония мер», которую издали после смерти автора — в 1722 году. Котс не придал ей большого значения и отобразил среди геометрических построений. Чтоб полученное Котсом выражение приобрело привычный вид, необходимо исправить ошибку в знаке и перевести на современный язык описания математики.

Формулу в привычном для людей виде опубликовал Эйлер в статье 1740 года. В 1748 году выражение было также представлено в его книге «Введение в анализ бесконечно малых». Эйлер доказал формулу на основе бесконечных разложений составляющих формулы в степенные ряды.

Но учёные того времени не рассматривали геометрической интерпретации формулы, которая используется на сегодняшний день. Представление о комплексных числах в виде точек на комплексной плоскости, на основе которого строится геометрическая интерпретация равенства, появилось примерно на 50 лет позже в работах К. Весселя.

Доказательство формулы

Вывод формулы Эйлера можно выполнить, используя ряд Маклорена – частный случай ряда Тейлора при разложении функции в окрестности точки x=0. Раскладывая левую часть равенства, получится cтепенной ряд, в котором в различные степени будет возводиться мнимая единица. Необходимо вынести её, сформировав коэффициент перед x.

При расчёте степеней мнимой единицы удаётся получить интересный эффект: если степень чётная – можно её представить как умножение некоторого числа пар i*i, которые можно заменить на -1 (из определения мнимой единицы). А при умножении между собой отрицательных единиц возможны два случая, опять же исходя из чётности их количества. Если их число кратно 2, то получают просто единицу («минус на минус даёт плюс»). Если их нечётное число – получится -1.

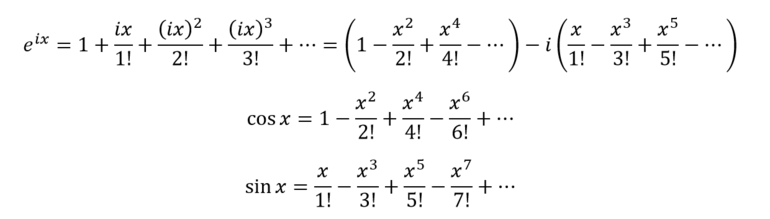
Таким образом, чередование происходит дважды: по чётности степеней мнимой единицы, а следом – по чётности степеней -1, которые были получены вследствие первого шага. Получается циклическое изменение на каждые четыре члена суммы.

После разделения мнимых и вещественных членов последовательности и расстановки чередующихся знаков формируются две группы слагаемых, которые представляют собой разложения других функций – синуса и косинуса. При их подстановке получится равенство Эйлера.

Что же такое число е и откуда оно взялось?

Кто-то спросит: «Что же это за число такое удивительное?» И здесь всего три слова: “второй замечательный предел”. На языке математики это выглядит следующим образом:

Расходимся…

Появление числа е связывают с Якобом Бернулли, который еще в 17 веке задался вопросом: какова же максимальная величина процентного дохода при постоянной капитализации вклада?

Якоб Бернулли (1654-1705)

Чтобы было понятно о чем идет речь, давайте представим, что у меня есть рубль. Я кладу его в банк под 100% годовых. То есть, через год у меня уже не рубль, а два.

Но что если рост происходит не мгновенно в конце года, а частями? Ну скажем, каждые полгода по 50%. Да, наш рубль так же превратится в два, но на 50 копеек, которые набежали за первые полгода, за вторую половину года набежит уже свой процент. И мы получим еще 25 копеек дополнительно. И в итоге мы имеем уже 2 рубля 25 копеек.

Если рост вклада будет происходить каждые четыре месяца, то есть 3 раза в год, дополнительный процент к нашим двум рублям, составит уже 37 копеек.

При ежемесячном росте только на процентах у нас набежит примерно 61 копейка.

И здесь возникает вопрос: а что если рост будет происходить непрерывно? Как в природе. К примеру, дети не вырастают на 15 сантиметров в свой день рождения. Нет. Они растут в течении всего года. Каждый день, каждый час, каждую секунду… Что если так же будет расти наш вклад, и вместе с ним будут увеличиваться начисления по проценту?

Существует ли какой то предел при непрерывном росте, который позволит понять, на какую максимальную прибыль мы можем рассчитывать?

Сам Бернулли определил, что это где-то между 2,5 и 3.

Леонард Эйлер (1707 – 1783)

Более точно этот предел вычислил Леонард Эйлер, а полученное число, к которому этот предел стремится, назвал числом е.

По одной из версий е — это первая буква в фамилии ученого (Euler). Но это не точно. Вполне возможно, что е это просто первая буква в слове«экспоненциальный» (exponential). Что тоже кажется тоже вполне разумным, так как экспонента, наверно, первая ассоциация при упоминании числа е. По крайней мере, у меня.

Определения комплексного возведения в степень

Экспоненциальная функция e x для действительных значений x может быть определена несколькими различными эквивалентными способами (см. Характеристики экспоненциальной функции ). Некоторые из этих методов могут быть непосредственно расширены, чтобы дать определения e z для комплексных значений z, просто подставив z вместо x и используя сложные алгебраические операции. В частности, мы можем использовать любое из трех следующих эквивалентных определений. С более продвинутой точки зрения, каждый из этих определений могут быть истолкован как предоставление уникального аналитического продолжения в е й в комплексную плоскость.

Определение дифференциального уравнения

Экспоненциальная функцией является единственной дифференцируемой функцией из комплексных переменных таким образом, что
z↦еz{\ Displaystyle г \ mapsto е ^ {г}}

dеzdzзнак равноеz{\ displaystyle {\ frac {de ^ {z}} {dz}} = e ^ {z}}

а также

езнак равно1.{\ displaystyle e ^ {0} = 1.}

Определение степенного ряда

Для комплексного z

еzзнак равно1+z1!+z22!+z33!+⋯знак равно∑пзнак равно∞zпп!.{\ displaystyle e ^ {z} = 1 + {\ frac {z} {1!}} + {\ frac {z ^ {2}} {2!}} + {\ frac {z ^ {3}} { 3!}} + \ Cdots = \ sum _ {n = 0} ^ {\ infty} {\ frac {z ^ {n}} {n!}}.}.}

Используя тест отношения , можно показать, что этот степенной ряд имеет бесконечный радиус сходимости и, таким образом, определяет e z для всех комплексных z .

Определение предела

Для комплексного z

еzзнак равноLimп→∞(1+zп)п.{\ displaystyle e ^ {z} = \ lim _ {n \ rightarrow \ infty} \ left (1 + {\ frac {z} {n}} \ right) ^ {n}.}

Здесь n ограничено положительными целыми числами , поэтому нет никаких сомнений в том, что означает степень с показателем n .

Экономика

При расчете сложных процентов число е возникает естественным образом.

Предположим, у вас есть определенная сумма денег п_или, инвестировать под процентную ставку i% годовых.

Если оставить деньги на 1 год, по истечении этого времени у вас будет:

P (1 год) = P_или + P_или.i = P_или (1+ я)

Еще через год, не прикасаясь к нему, вы получите:

P (2 года) = P_или + P_или.i + (P_или + P_или i) я = P_или + 2P_или.i + P_или.я2  = Ро (1 + я)2

И продолжая таким образом п лет:

P = P_или (1 + я)п

Теперь вспомним одно из определений e:

Это немного похоже на выражение для P, поэтому должна быть связь.

Распределяем номинальную процентную ставку я в п периодов времени, таким образом, сложная процентная ставка будет i / n:

P = P_или [1+ (i / n)]п

Это выражение немного больше похоже на наш предел, но все же не совсем то же самое.

Однако после некоторых алгебраических манипуляций можно показать, что, сделав эту замену переменной:

ч = п / я → я = п / ч

Наши деньги P становятся:

P = P_или [1+ (1 / час)]Здравствуй = п_или {[1+ (1 / час)]час}я

А что между клавишами, даже если написано буквой час, равно аргументу предела, определяющему число e, пропуская только при переходе к пределу.

Давайте сделаемчас → ∞, а то, что находится между фигурными скобками, становится числом а также. Это не означает, что нам нужно бесконечно долго ждать, чтобы вывести деньги.

Если присмотреться, при выполнении ч = п / я и стремясь к ∞, мы фактически распределили процентную ставку в очень и очень маленькие промежутки времени:

я = н / ч

Это называется непрерывное компаундирование. В таком случае сумму денег легко рассчитать так:

P = P_или .а такжея

Где i — годовая процентная ставка. Например, при внесении 12 евро под 9% в год посредством непрерывной капитализации через год у вас есть:

P = 12 x e0.09×1 € = 13.13 €

При выигрыше 1,13€.

ЧИСЛО Е | Энциклопедия Кругосвет

ЧИСЛО e. Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e–kt, где k – число, характеризующее скорость распада данного вещества. Обратная величина 1/k называется средним временем жизни атома данного вещества, так как в среднем атом прежде, чем распасться, существует в течение времени 1/k. Величина 0,693/k называется периодом полураспада радиоактивного вещества, т.е. временем, за которое распадается половина исходного количества вещества; число 0,693 приближенно равно log_e 2, т.е. логарифму числа 2 по основанию e. Аналогично, если бактерии в питательной среде размножаются со скоростью, пропорциональной их числу в настоящий момент, то по истечении времени t начальное количество бактерий N превращается в Nekt. Затухание электрического тока I в простом контуре с последовательным соединением, сопротивлением R и индуктивностью L происходит по закону I = Ie–kt, где k = R/L, I – сила тока в момент времени t = 0. Аналогичные формулы описывают релаксацию напряжений в вязкой жидкости и затухание магнитного поля. Число 1/k часто называют временем релаксации. В статистике величина e–kt встречается как вероятность того, что за время t не произошло событий, наступающих случайно со средней частотой k событий в единицу времени. Если S – сумма денег, вложенных под r процентов с непрерывным начислением вместо начисления через дискретные промежутки времени, то к моменту времени t первоначальная сумма возрастет до Setr/100.

Причина «вездесущности» числа e заключается в том, что формулы математического анализа, содержащие экспоненциальные функции или логарифмы, записываются проще, если логарифмы брать по основанию e, а не 10 или какому-либо другому основанию. Например, производная от log₁₀ x равна (1/x)log₁₀ e, тогда как производная от log_e x равна просто 1/x. Аналогично, производная от 2x равна 2xlog_e 2, тогда как производная от eх равна просто ex. Это означает, что число e можно определить как основание b, при котором график функции y = log_b x имеет в точке x = 1 касательную с угловым коэффициентом, равным 1, или при котором кривая y = bx имеет в x = 0 касательную с угловым коэффициентом, равным 1. Логарифмы по основанию e называются «натуральными» и обозначаются ln x. Иногда их также называют «неперовыми», что неверно, так как в действительности Дж.Непер (1550–1617) изобрел логарифмы с другим основанием: неперов логарифм числа x равен 107 log_1/e (x/107) (см. также ЛОГАРИФМ).

Различные комбинации степеней e встречаются в математике так часто, что имеют специальные названия. Таковы, например, гиперболические функции

График функции y = ch x называется цепной линией; такую форму имеет подвешенная за концы тяжелая нерастяжимая нить или цепь. Формулы Эйлера

где i2 = –1, связывают число e с тригонометрией. Частный случай x = p приводит к знаменитому соотношению eip + 1 = 0, связывающему 5 наиболее известных в математике чисел.

При вычислении значения e могут быть использованы и некоторые другие формулы (чаще всего пользуются первой из них):

Значение e с 15 десятичными знаками равно 2,718281828459045. В 1953 было вычислено значение e с 3333 десятичными знаками. Символ e для обозначения этого числа был введен в 1731 Л.Эйлером (1707–1783).

Десятичное разложение числа e непериодично (e – иррациональное число). Кроме того, e, как и p, – трансцендентное число (оно не является корнем никакого алгебраического уравнения с рациональными коэффициентами). Это доказал в 1873 Ш.Эрмит. Впервые было показано, что столь естественным образом возникающее в математике число является трансцендентным.

Проверь себя!Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Откуда взялось число Эйлера e?

Число, представленное буквой e, было обнаружено математиком Леонардом Эйлером как решение проблемы, поставленной другим математиком, Якобом Бернулли, 50 лет назад. Проблема Бернулли была финансовой.

Предположим, вы кладете 1000 долларов в банк, который выплачивает 100% годовых по сложным процентам, и оставляете их там на год. У вас будет 2000 долларов. Теперь предположим, что процентная ставка вдвое меньше, но банк выплачивает ее дважды в год. В конце года у вас будет 2250 долларов. Теперь предположим, что банк платил только 8,33%, что составляет 1/12 от 100%, но платил 12 раз в год. В конце года у вас будет 2613 долларов. Общее уравнение для этой прогрессии:

\ bigg (1 + \ frac {r} {n} \ bigg) ^ n

гдерравно 1, а n — период выплаты.

Оказывается, когда n приближается к бесконечности, результат становится все ближе и ближе к e, которое составляет 2,7182818284 с точностью до 10 знаков после запятой. Вот как это открыл Эйлер. Максимальный доход, который вы можете получить от инвестиции в размере 1000 долларов в год, составит 2718 долларов.

Когда EI не применяют

Если данные имеют количественный характер и не распределены нормально, то используют другие методы для сравнения групп, такие как критерий Манна-Уитни или критерий Краскела-Уоллиса.

Когда группы не являются независимыми, применение EI не подходит. Например, если изучается эффект лечения на одном и том же пациенте в разные моменты времени, то необходимо использовать критерий отличия среднего значения.

Если данные содержат выбросы, то применение EI может дать искаженные результаты. В таких случаях используют методы, устойчивые к выбросам, например, медианный тест Уилкоксона или критерий Брауна-Форсайта.

Если размеры выборок слишком малы, то степень надежности результата EI может быть низкой. В таких ситуациях лучше использовать методы, которые не требуют большого количества данных, например, точечные оценки или интегральные тесты.

В целом, применение EI не является универсальным методом для сравнения групп и нужно учитывать особенности данных для выбора правильного критерия.

Что такое экспонента в математике для чайников

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

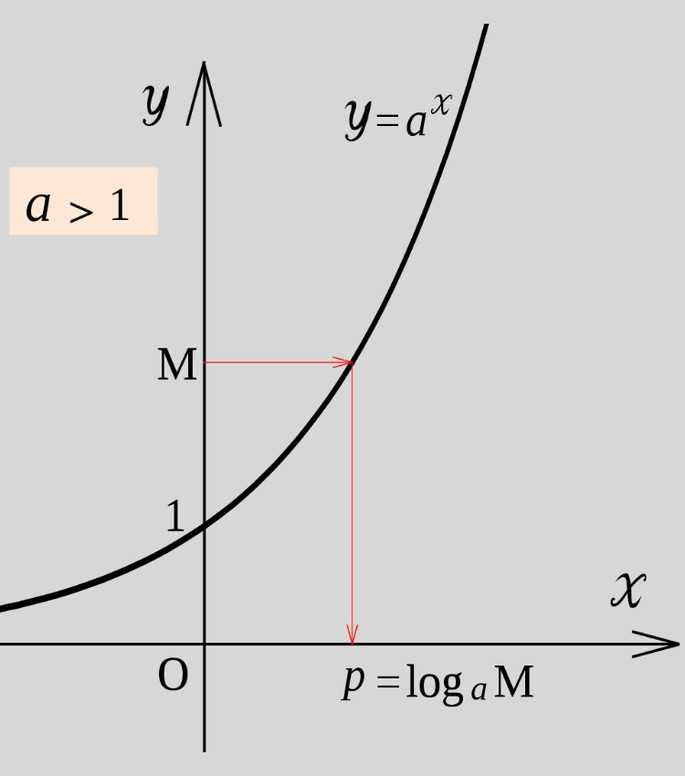
Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Мнемоника[править | править код]

• Приблизительное значение зашифровано в: «Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли» (то есть 2,718281828459 )
• Запомнить как 2, 71, и повторяющиеся 82, 81, 82
• Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (), затем углы равнобедренного (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой»
• Цифры 45, 90 и 45 можно запоминать как «год победы над фашистской Германией, затем дважды этот год и снова он»
• Правила e связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США,  — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.
• С точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6 − 4, 6 − 2, 6 − 1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки): 666245≈2,718{666 \over 245} \approx 2,718.
• Запоминание e как 66610⋅666−13\frac{666}{10 \cdot \sqrt{666} — 13}.
• Грубое (с точностью до 0,001), но красивое приближение полагает e равным π⋅cos Косинус π6\pi \cdot \cos {\pi \over 6}. Совсем грубое (с точностью 0,01) приближение даётся выражением 5⋅π−135 \cdot \pi — 13.
• «Правило Боинга»: e≈4⋅sin Синус ,747e \approx 4 \cdot \sin 0,747 даёт неплохую точность 0,0005.
• Формулы Г. Александрова: e≈3−563 e \, \approx \, 3 \, — \, \sqrt {\frac {5}{63}} — дает верные семь первых цифр, а e≈3−9394337\,e \, \approx \, 3 — \frac {93}{94} \sqrt { \frac {3}{37}} вычисляет константу с точностью 4,6⋅10−10 4,6 \, \cdot \, 10^{-10}.
• Стишки:

Два и семь, восемнадцать,

Двадцать восемь, восемнадцать,

Двадцать восемь, сорок пять,

Девяносто, сорок пять.

Определение EI

EI в математике – это показатель эластичности. Он применяется в механике и строительстве для описания степени гибкости материалов. EI означает “Modulus of Elasticity times Moment of Inertia” (модуль упругости, умноженный на момент инерции).

Модуль упругости, в свою очередь, показывает, насколько деформируется материал при наложении на него силы. Чем больше модуль упругости, тем меньше материал деформируется.

Таким образом, показатель EI позволяет определить, насколько гибким является конструкция или материал. Чем выше EI, тем жестче материал и чем ниже – тем более гибкий он.

Интересные факты[]

• В IPO компании в 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленная цифра представляет собой первые 10 цифр известной математической константы.
• В языках программирования символу e{\displaystyle e} в экспоненциальных записях числовых литералов соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка для математических вычислений FORTRAN:

Таким образом, записи типа в языках программирования будет соответствовать число 7,38×10−43{\displaystyle 7{,}38\times 10^{-43}}, а не 7,38×e−43{\displaystyle 7{,}38\times e^{-43}}.

Выводы о EI

Таким образом, можно сделать несколько выводов о EI в математике:

• EI — это показатель жесткости балки.
• Чем больше значение EI, тем жестче балка.
• EI зависит от геометрических параметров балки и материала, из которого она сделана.
• Для расчета EI необходимо знать модуль упругости материала и момент инерции сечения балки.
• Расчет EI может быть осуществлен как аналитически, так и с помощью компьютерных программ.
• Корректный расчет EI необходим для обеспечения безопасности конструкций, которые включают в себя балки.

Изучение EI является важным элементом инженерного и конструкционного проектирования, поскольку это позволяет спроектировать конструкцию с нужным уровнем жесткости и безопасности. Также это помогает определить необходимую толщину и геометрию балки.

Наконец, изучение EI может быть полезным для студентов и дипломников, которые занимаются конструкционным проектированием или строительством.