Что такое Экспонента
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
График экспоненты выглядит следующим образом:
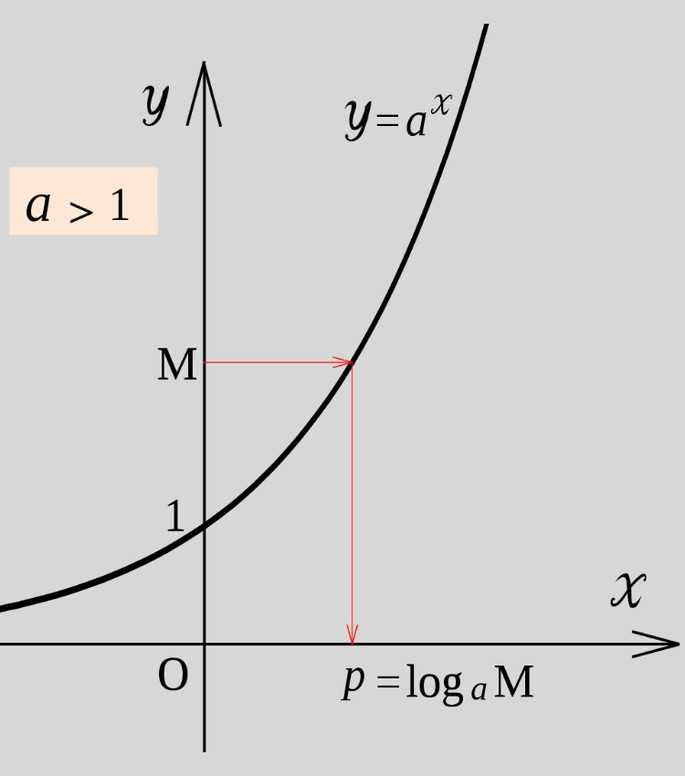
Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
Второй замечательный предел
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е. Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
- через сумму ряда;
- через формулу Муавра — Стирлинга;
- другие.
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.
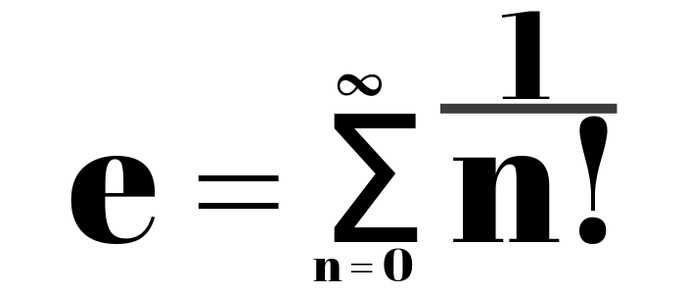
Можно получить приближение е, рассчитав первые 7 частей этой суммы:
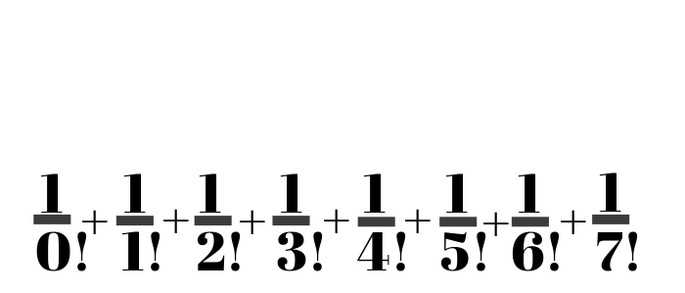
И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:
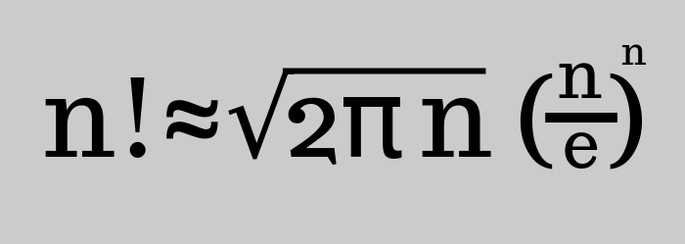
И в этом случае чем больше n, тем точнее будет результат.
Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 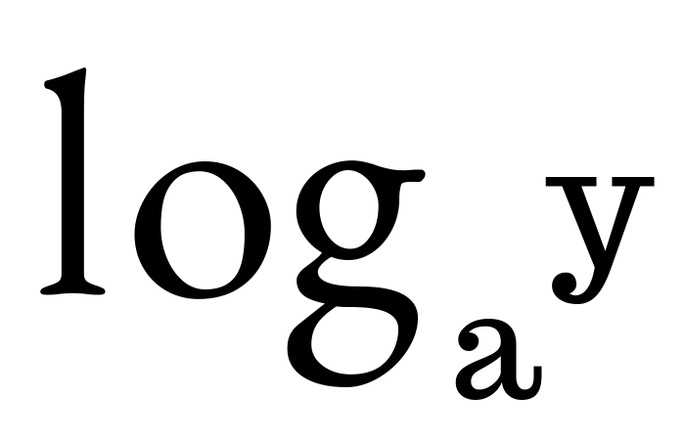 .
.
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Джон Непер — шотландский математик (1550–1617 гг.)
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Леонард Эйлер — швейцарский математик (1707–1783 гг.)
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Свойства
- (ex)’ = ex, в частности
- Экспонента является единственным решением дифференциального уравнения y‘ = y с начальными данными y(0) = 1. Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
- Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
- Экспонента является выпуклой функцией.
- Обратная функция к ней — натуральный логарифм .
- Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
- Основное функциональное свойство экспоненты:exp(a + b) = exp(a)exp(b)
Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.
.
Естественная экспоненциальная функция

Это функция, в основе которой лежит число e или число Эйлера, иррациональное число, значение которого:
е = 2,718181828 …
Эта база, хотя и не является круглым числом, очень хорошо подходит для многих приложений. Поэтому он считается самым важным основанием всех экспоненциальных функций. Естественная экспоненциальная функция математически выражается как:
f (x) = eИкс
Экспоненциальная функция часто появляется в Probability and Statistics, поскольку различные распределения вероятностей, такие как нормальное распределение, распределение Пуассона и другие, могут быть выражены через экспоненциальные функции.
И что все это значит
Экспонента — это наибольший возможный результат стопроцентного непрерывного роста за конкретный период времени. Да, изначально нам обещают 100% прибыли, то есть всего $2, но каждый цент приносит свои дивиденды и по итогам у нас оказывается ровно $2,71828 прибыли. Число е – это максимум, который мы можем получить при разбиении прибыли на суммы бесконечно малых величин.
Это означает, что если при потенциальной стопроцентной прибыли мы вложим в бизнес $1, то получим $2,718 чистой прибыли. Если $2, то мы получим 2е чистой прибыли, а если $100, то наш профит составит 100е. Таким образом, e — это предельная константа, которая ограничивает процессы роста точно так же, как скорость света ограничивает передвижение информации в пространстве. Число е – это максимально возможный результат, труднодостижимый на практике, поэтому в реальности многие процессы описываются с использованием частей экспоненты.
Формальное определение
Показательная функция (синим цветом) и сумма первых
n + 1
членов ее степенного ряда (красным цветом).
Действительная экспоненциальная функция может быть охарактеризована множеством эквивалентных способов. Обычно это определяется следующим степенным рядом : exp : р → р { Displaystyle ехр двоеточие mathbb {R} to mathbb {R}}
exp Икс знак равно ∑ k знак равно 0 ∞ Икс k k ! знак равно 1 + Икс + Икс 2 2 + Икс 3 6 + Икс 4 24 + ⋯ { displaystyle exp x: = sum _ {k = 0} ^ { infty} { frac {x ^ {k}} {k!}} = 1 + x + { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {6}} + { frac {x ^ {4}} {24}} + cdots}
Так как радиус сходимости этого степенного ряда бесконечен, это определение фактически применимо ко всем комплексным числам z ∈ ℂ (см. § Комплексная плоскость для продолжения до комплексной плоскости). Тогда постоянная e может быть определена как exp Икс { Displaystyle ехр х} е знак равно exp 1 знак равно ∑ k знак равно 0 ∞ ( 1 / k ! ) . { textstyle e = exp 1 = sum _ {k = 0} ^ { infty} (1 / k!).}
Почленное дифференцирование этого степенного ряда показывает, что для всех действительных x , что приводит к еще одной общей характеристике как единственного решения дифференциального уравнения d d Икс exp Икс знак равно exp Икс { Displaystyle { гидроразрыва {d} {dx}} ехр х = ехр х} exp Икс { Displaystyle ехр х}
y ′ ( Икс ) знак равно y ( Икс ) , { Displaystyle у ‘(х) = у (х),}
удовлетворяющий начальному условию y ( 0 ) знак равно 1. { displaystyle y (0) = 1.}
Основываясь на этой характеристике, цепное правило показывает, что его обратная функция, натуральный логарифм , удовлетворяет для или Это соотношение приводит к менее распространенному определению действительной экспоненциальной функции как решения уравнения d d y бревно е y знак равно 1 / y { displaystyle { frac {d} {dy}} log _ {e} y = 1 / y} y > 0 , { displaystyle y> 0,} бревно е y знак равно ∫ 1 y 1 т d т . { textstyle log _ {e} y = int _ {1} ^ {y} { frac {1} {t}} , dt.} exp Икс { Displaystyle ехр х} y { displaystyle y}
Икс знак равно ∫ 1 y 1 т d т . { displaystyle x = int _ {1} ^ {y} { frac {1} {t}} , dt.}
Посредством биномиальной теоремы и определения степенного ряда экспоненциальная функция также может быть определена как следующий предел:
exp Икс знак равно Lim п → ∞ ( 1 + Икс п ) п . { displaystyle exp x = lim _ {n to infty} left (1 + { frac {x} {n}} right) ^ {n}.}
Что такое Экспонента
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
График экспоненты выглядит следующим образом:

Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
Второй замечательный предел
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е. Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
- через сумму ряда;
- через формулу Муавра — Стирлинга;
- другие.
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.
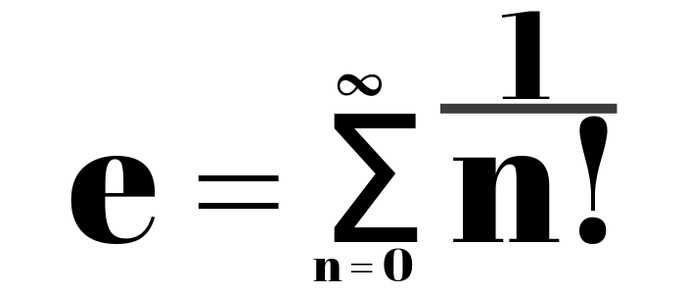
Можно получить приближение е, рассчитав первые 7 частей этой суммы:
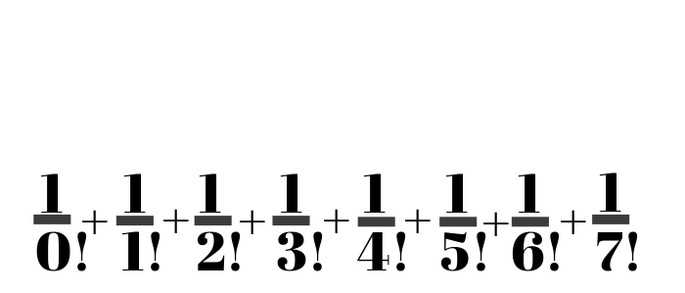
И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:
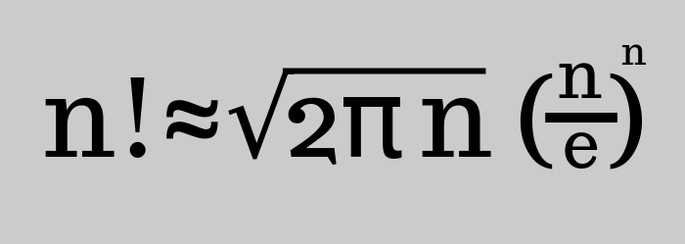
И в этом случае чем больше n, тем точнее будет результат.
Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 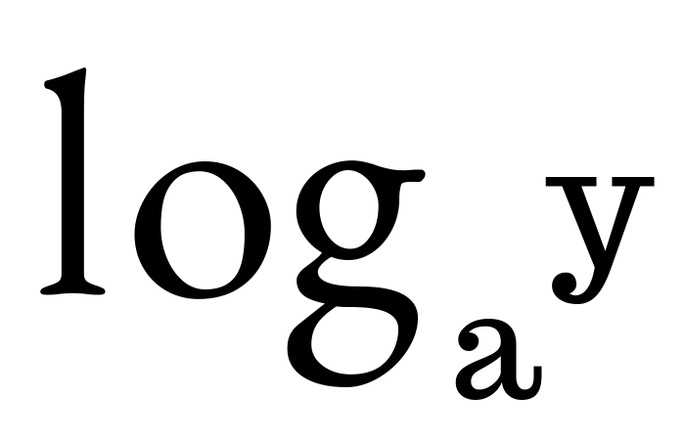 .
.
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Джон Непер — шотландский математик (1550–1617 гг.)
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Леонард Эйлер — швейцарский математик (1707–1783 гг.)
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Приглядимся поближе
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
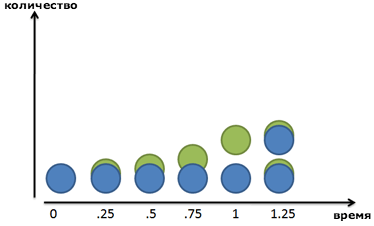
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
Показательная форма записи экспоненты
Экспонента – это функция, которая играет важную роль в математике и естественных науках. Она обозначается символом e. Экспонента показывает, насколько быстро растет или убывает некоторое значение приращения.
Показательная форма записи экспоненты очень упрощает работу с числами, которые возрастают или убывают экспоненциально. В этой форме экспонента записывается как ax, где a – основание экспоненты, а x – показатель степени.
В показательной форме записи экспонента, основание a – положительное число и не равно 1, а показатель степени x – любое число, включая дроби и отрицательные значения.
Если показатель степени x является натуральным числом, то экспонента показывает, сколько раз нужно умножить основание a на само себя. Например, если a = 2 и x = 3, то экспонента будет равна 23 = 2 * 2 * 2 = 8.
Если показатель степени x является дробным числом, то экспонента определяется с помощью корня из основания a. Например, если a = 2 и x = 1/2, то экспонента будет равна 21/2 = √2 ≈ 1,414.
Если показатель степени x является отрицательным числом, то экспонента определяется с помощью обратного значения основания a. Например, если a = 2 и x = -2, то экспонента будет равна 2-2 = 1/22 = 1/4.
В показательной форме записи экспоненты, основание a может быть любым числом, но самым распространенным является число e ≈ 2.71828. Это основание экспоненты называется числом Эйлера и имеет множество математических свойств и применений.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Джон Непер — шотландский математик (1550–1617 гг.)
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Леонард Эйлер — швейцарский математик (1707–1783 гг.)
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Узнайте также, что такое Число Пи, Натуральные числа и Логарифм.
Смысл числа e
Число Пи представляет собой не просто иррациональное число, равное 3,1415, а одинаковое для всех случаев соотношение длины окружности к диаметру. Точно так же и число e имеет свой собственный смысл.
Экспонента — это базовое соотношение роста для всех растущих процессов. Любое число можно рассматривать как увеличенную единицу, любой квадрат — как масштабированный единичный квадрат, любой равносторонний треугольник — как увеличенный или уменьшенный правильный треугольник, ну а любой коэффициент роста можно представить в виде масштабированного коэффициента е.
Именно операции с числом e дадут вам возможность определить темпы роста в таких ситуациях, как прирост населения, начисление процентов по депозиту или объем полураспада радиоактивного вещества.
Экспонента: определение, формула, свойства, график
В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
- Определение и формула экспоненты
- График экспоненты
- Свойства экспоненциальной функции
Определение и формула экспоненты
Экспонента – это показательная функция, формула которой выглядит следующим образом:
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:

График экспоненты
Ниже представлен график экспоненциальной функции
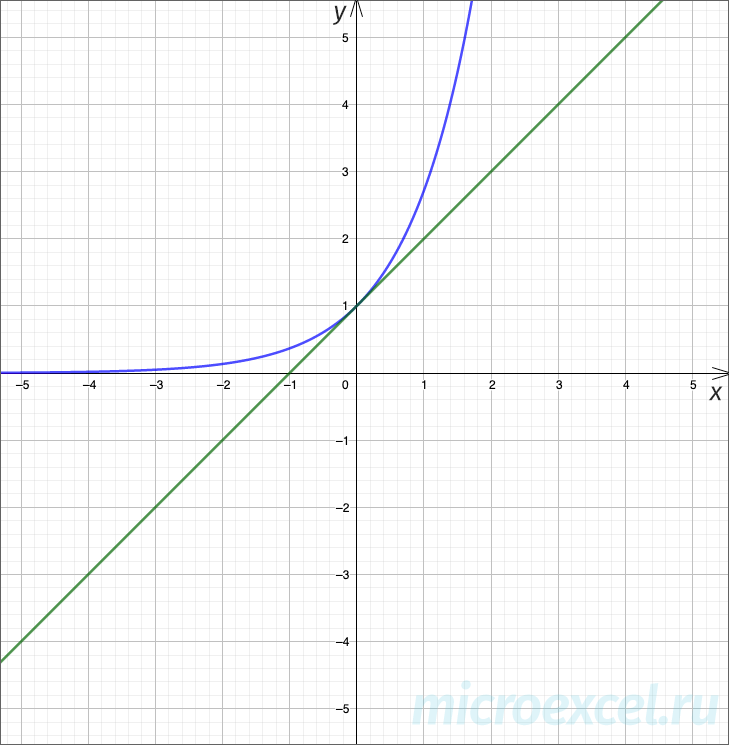
Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y .
Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox , но никогда не пересечет и не коснется ее.
Пересечение с осью ординат Oy – в точке , так как
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Интересные факты
Экспоненциальную функцию также называют показателем степени.
Показательная функция — это функция вида y=a×, где a — заданное число (основное число), x — переменная.
А если основание = е, то с переменной х логарифм записывается математически как ln, а не как log. И это называется натуральным логарифмом (логарифмом по основанию e):
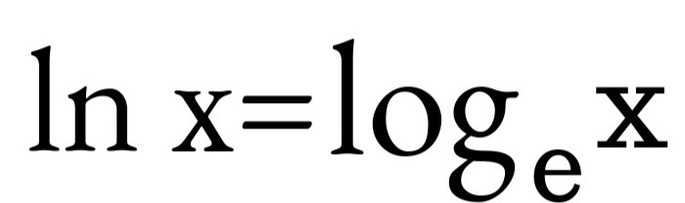
Логарифмическая функция, обратная показательной функции y = a ×, a > 0, a ≠ 1, записывается как 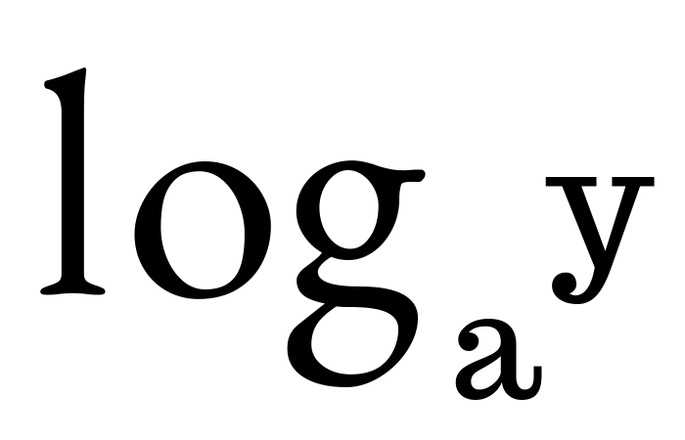
.
Производная и первообразная экспоненциальной функции равны самой себе, т.е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчетах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Экспонента: определение, формула, свойства, график
В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
- Определение и формула экспоненты
- График экспоненты
- Свойства экспоненциальной функции
Определение и формула экспоненты
Экспонента – это показательная функция, формула которой выглядит следующим образом:
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:

График экспоненты
Ниже представлен график экспоненциальной функции

Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y .
Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox , но никогда не пересечет и не коснется ее.
Пересечение с осью ординат Oy – в точке , так как
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Использование экспоненты на практике
На первый взгляд рост изображается в виде прибавления 1%, однако, математически такая прибавка выражается как умножение на 1,01. Таким образом, при операциях с числом e мы используем степени или корни. Или натуральные логарифмы, если нам необходима обратная операция. Какой бы коэффициент прироста мы не взяли, он будет означать степень для числа е. К примеру, если мы знаем, что в течение 3 лет получим прибыль в размере 200%, то мы просто умножаем прирост (e 2) на 3 периода и получаем:
Рост = (е 3) 2 = e 6
Для лучшего понимания рассмотрим примеры.
Депозит в банке
Допустим, мы положили на депозит в банке $100 под годовую ставку в размере 8%. Выбранный банк предлагает нам полную капитализацию процентов, какую же прибыль мы получим через 5 лет? Так как банк обеспечивает нам непрерывный рост денег, через 5 лет на нашем счету уже будет:
Прибыль = 100 × е (0,08 × 5) = 149,1
Потрясающе, правда? К сожалению, реальные банки редко используют сложные проценты, а если и рассчитывают капитализацию, то по своим формулам, которые несколько отличаются от классической экспоненты.
Период полураспада
Представьте, что у вас есть 5 кг радиоактивного урана, который распадается со скоростью 100% в год. Сколько урана у вас останется через 2 года? По идее, весь уран должен распасться за первый же год, однако это не так. Через 6 месяцев у вас останется только 2,5 кг урана, который в свою очередь начнет распадаться со скоростью всего 2,5 кг в год. Еще через пару месяцев в вашем хранилище останется 1 кг урана, но и он будет распадаться с еще меньшей скоростью на уровне 1 кг в год. С течением времени вы теряете радиоактивное топливо, при этом снижается и скорость распада. Таким образом, через 2 года у вас останется:
Радиоактивный остаток = 5 × e −2 = 0,676
Заключение
Экспонента находит широкое применение в ситуациях, где что-либо непрерывно или дискретно растет. Вы можете использовать калькулятор возведения числа e в степень для подсчета результатов роста любых непрерывных процессов.
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP
. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
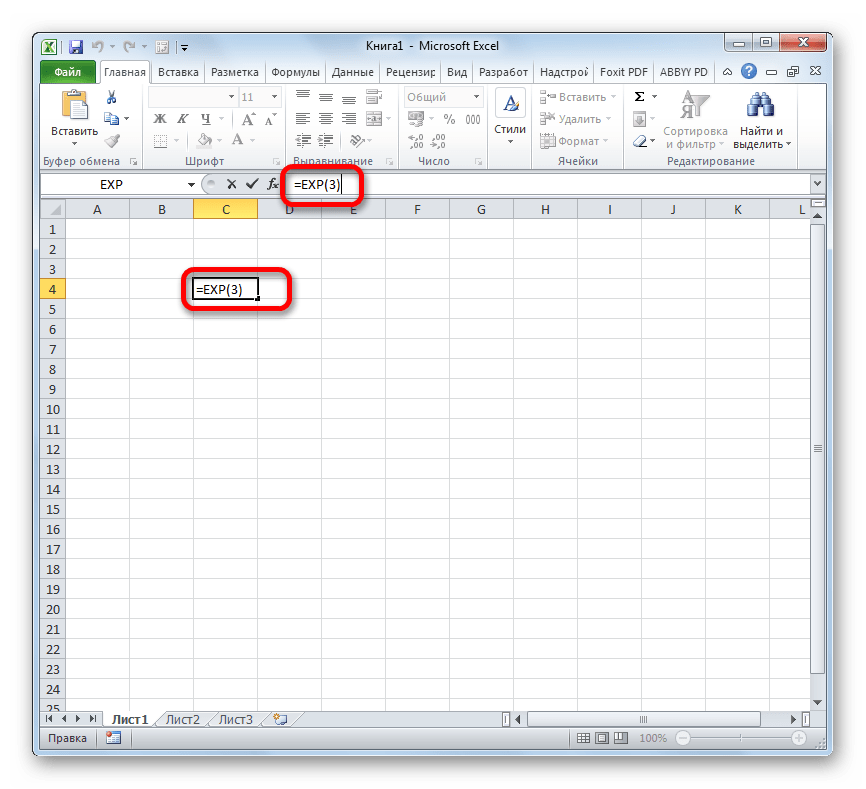
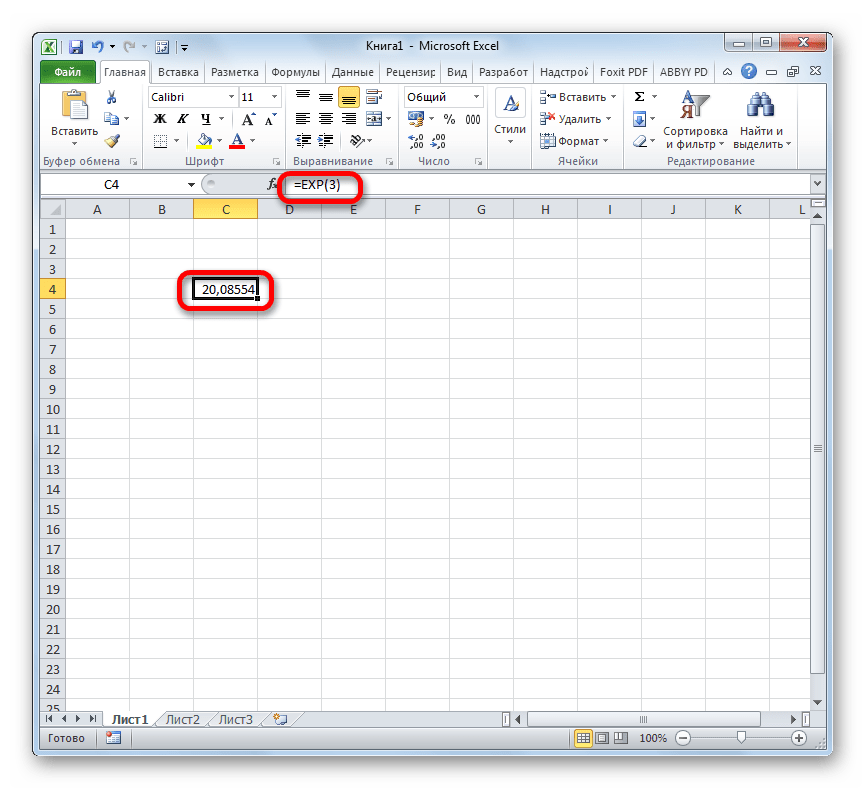
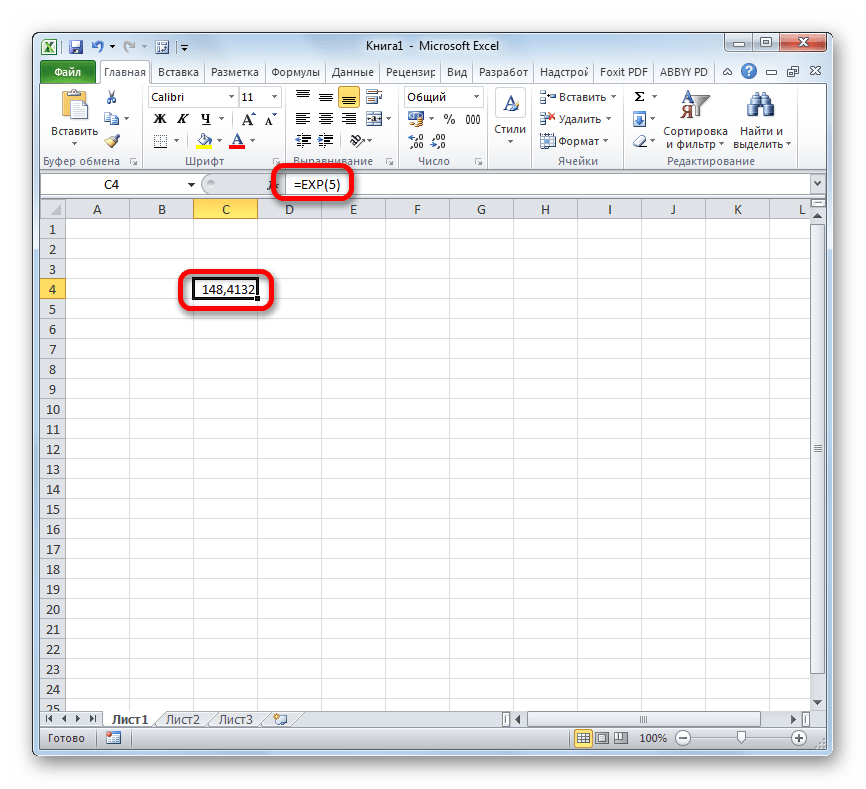
Способ 1: вычисление экспоненты при помощи ручного ввода функции
EXP(число)
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
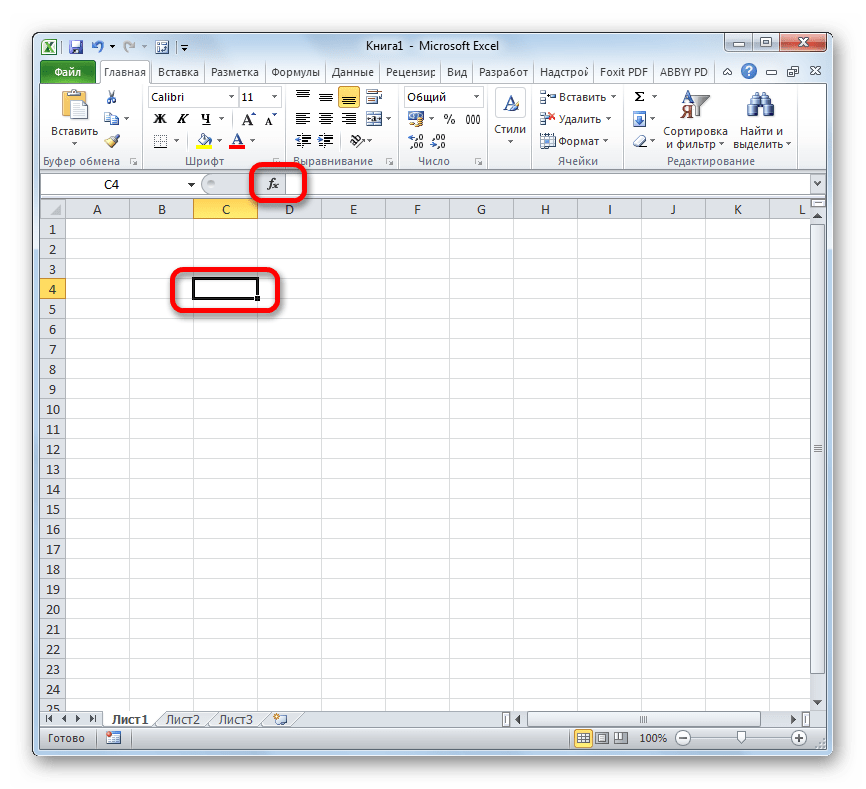
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций
. Рассмотрим, как это делается на примере.
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число»
и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK»
.
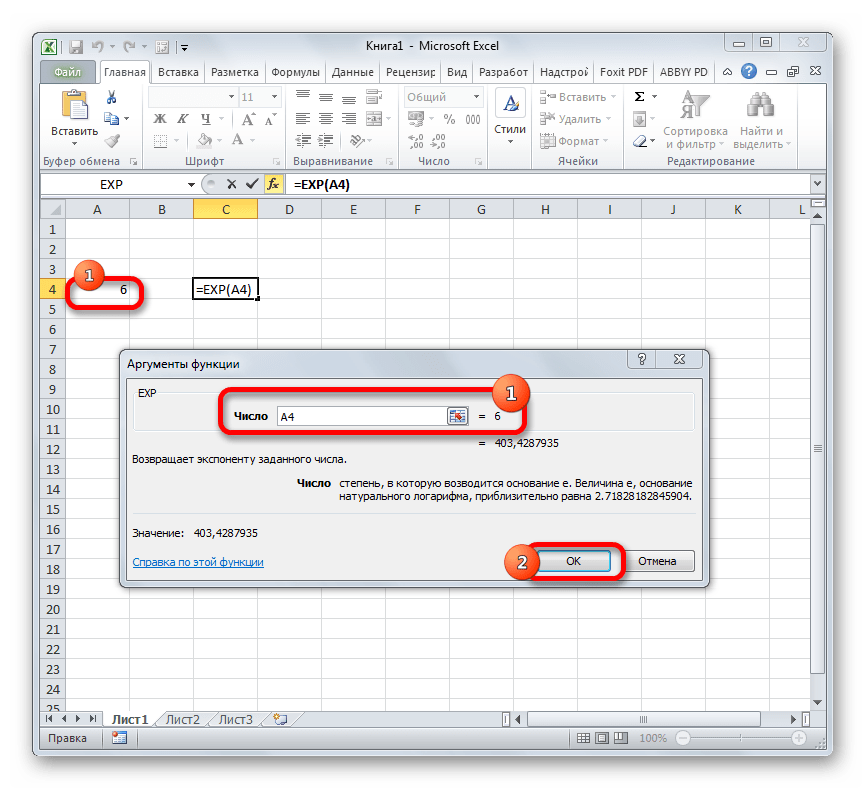
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
(x)
= e x
Экспоненту обозначают так ,
или .
Число e
Основанием степени экспоненты является число e
. Это иррациональное число. Оно примерно равное
≈ 2,718281828459045…
Число e
определяется через предел последовательности. Это, так называемый, второй замечательный предел
:.
Также число e
можно представить в виде ряда:.
И что все это значит
Экспонента — это наибольший возможный результат стопроцентного непрерывного роста за конкретный период времени. Да, изначально нам обещают 100% прибыли, то есть всего $2, но каждый цент приносит свои дивиденды и по итогам у нас оказывается ровно $2,71828 прибыли. Число е – это максимум, который мы можем получить при разбиении прибыли на суммы бесконечно малых величин.
Это означает, что если при потенциальной стопроцентной прибыли мы вложим в бизнес $1, то получим $2,718 чистой прибыли. Если $2, то мы получим 2е чистой прибыли, а если $100, то наш профит составит 100е. Таким образом, e — это предельная константа, которая ограничивает процессы роста точно так же, как скорость света ограничивает передвижение информации в пространстве. Число е – это максимально возможный результат, труднодостижимый на практике, поэтому в реальности многие процессы описываются с использованием частей экспоненты.
Дискретный рост
В качестве базового примера системы непрерывного удвоения можно привести размножение бактерий, которые удваиваются каждые сутки. Если удвоение происходит один раз, то математически мы получаем 2 в первой степени, то есть просто 2. Если удвоений x раз, то в итоге мы получаем 2 в степени x бактерий, денег или любого другого добра.
Однако система может изменяться не в 2 раза, а например на 20% или 120%. В этом случае мы можем представить удвоение не как двойку, а как 1+1 или 1+100%. В такой записи мы можем подставить любой коэффициент прироста и получить формулу роста как:
Рост = (1 + прирост) x ,
где x — это количество циклов прироста.
Благодаря этой формуле мы можем узнать, сколько бактерий мы получим из одной клетки через 30 дней. Однако бактерии делятся дискретно, то есть пока новая клетка не сформируется в течение суток, она не сможет производить новые организмы. Применяя эту формулу к деньгам, мы получим совсем другой результат.
Понятие экспоненциального роста
Давайте начнем с рассмотрения базовой системы, которая удваивается
за определенный период времени. Например:
- Бактерии делятся и «удваиваются» в количестве каждые 24 часа
- Мы получаем вдвое больше лапшинок, если разламываем их пополам
- Ваши деньги каждый год увеличиваются вдвое, если вы получаете 100% прибыли (везунчик!)
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
рост
= 2 x
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
рост
= (1+100%) x
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
рост
= (1+прирост
) x
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.































