Пример задач на использование формул разности квадратов и суммы и разности кубов
Пример 4
Разложить на множители.
а) ${(a+5)}^2-9$
в) $-x^3+\frac{1}{27}$
Решение:
а) ${(a+5)}^2-9$
\
Применяя формулу разности квадратов, получим:
\
Запишем данное выражение в виде:
Применим формулу кумы кубов:
в) $-x^3+\frac{1}{27}$
Запишем данное выражение в виде:
\
Применим формулу кумы кубов:
\
Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.
Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.
Квадрат суммы
Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
Квадрат разности
Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
Разность квадратов
Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).
Куб суммы
Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.
Сумма кубов
Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).
Пример.
Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.
Если значения сторон небольшие, то выполнить вычисления просто.
Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.
Куб разности
Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.
Разность кубов
Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).
Пример.
Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.
Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.
Разность кубов двух выражений
Найдем продукт двучлена
и трехчлена
. По правилу умножения многоэлементного на многоэлементное получаем:
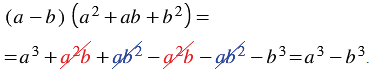
Итак, мы получили тождество:
, которые находят формулой разности кубов двух врезей.
Многочлен
, стоящий в правой части, выглядит как многочленный
, что равно квадрату суммы
и
, так много членов
найти непольским квадратом суммы.
Правило:
| Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. |
Пример:
Разместите на множители .
Решение:
Используя свойства степеней, представим этот полином как разность кубов двух выражений, получим:
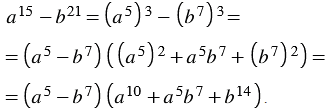
Дополнительные формулы сокращенного умножения
К таблице базовых ФСУ следует добавить еще несколько важных тождеств, полезных для решения задач.
Бином Ньютона
Формула разложения на отдельные члены всей неотрицательной степени суммы двух переменных. Записано так: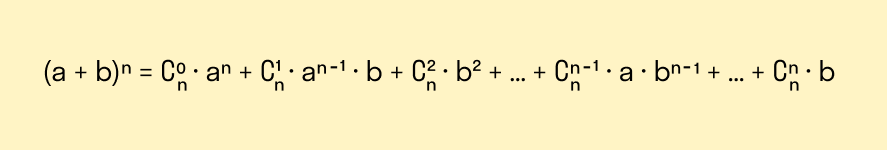
Пример расчета биномиальных коэффициентов, стоящих в очереди под номером n в треугольнике Паскаля: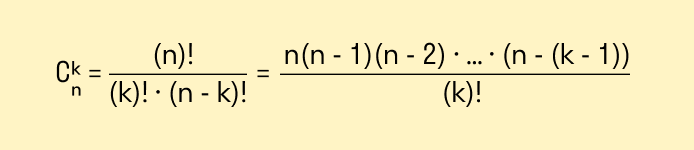
ФСУ для кварта и куба суммы и разности — частные случаи биномиальной формулы Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Полезно, если сумма сумм, которые нужно возвести в степень, больше двух.
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+2*ан-1*ан
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
ан − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частные кассовые работы разности квартир и кубов при n = 2 и n = 3.
Примеры применения ФСУ
Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.
Пример 1. ФСУ
Упростим выражение 9 y — (1 + 3 y) 2 .
Применим формулу суммы квадратов и получим:
9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2
Пример 2. ФСУ
Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .
Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.
8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .
Сокращаем и получаем:
8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z
Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.
Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:
79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .
Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.
Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.
Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.
Квадрат суммы
Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
Квадрат разности
Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
Разность квадратов
Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).
Куб суммы
Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 – b2 = (a – b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a – b) * (a + b) = a2 – b2.
Важно знать, что разность квадратов не равна квадрату разности: a2 – b2 ≠ (a – b)2. Докажем, что a2 – b2 = (a – b) * (a + b)
Докажем, что a2 – b2 = (a – b) * (a + b).
Поехали:
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b – a * b = 0
a2 – b2 = a2 – b2 + ab – ab
- Сгруппируем иначе: a2 – b2 + a * b – a * b = a2 – a * b + a * b – b2
- Продолжим группировать: a2 – a * b – b2 +a * b = (a2 – a * b) + (a * b – b2)
- Вынесем общие множители за скобки:
(a2 – a * b) + (a * b – b2) = a *(a – b) + b *(a – b)
- Вынесем за скобки (a – b). a * (a – b) + b * (a – b) = (a – b) * (a + b)
- Результат доказательства: a2 – b2 = (a – b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a – b) * (a + b) = a2 – b2, нужно раскрыть скобки: (a – b) * (a + b) = a * a + a * b – b * a – b * b = a2 – b2.
Остальные ФСУ можно доказать аналогичным методом.
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
(a − b)(a + b)
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
То есть выражение (a − b)(a + b) равно a2 − b2
(a − b)(a + b) = a2 − b2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:
(2x − 5)(2x + 5) = (2x)2 − 52
Вычислим правую часть, получим 4×2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4×2 − 25
Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4×2 − 25
(2x − 5)(2x + 5) = 4×2 − 10x + 10x − 25 = 4×2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16×2 − 25y2
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.
Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.
Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9×2 − 49
Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.
Далее вычисляем выражение в скобках:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25×2 − 9y2)
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25×2 − 9y2) = −25×2 + 9y2
УПРАЖНЕНИЯ
1. а) Известно, что a и b — цифры. Выпишите формулу, выражающую число х, состоящее из a сотен, 7 десятков и b единиц:
1) х=100b+70+a; 2) x=100a+70+b; 3) x=ab; 4)x=700+10a+b. б) Известно, что m и n — цифры. Выпишите формулу, выражающую число у, состоящее их 5 сотен, m десятков и n единиц: 1) y=100m+50+n; 2)y=100n+50+m; 3) y=5mn; 4) y=500+10m+n.
Решение:а) а сотен — это 100а, 7 десятков — это 70, b единиц — это просто b. Число х=100а+70+b/Ответ: 2)
2. а) Известно, что s-t=-1,3. Укажите выражение, значение которого равно 2,6:1) (t-s)2; 2)
(t-s):2; 3) 2(t-s); 4) s-t-1,3. б) Известно, что m-n=-2,1. Укажите выражение, значение которого равно 4,2:1) (n-m)2; 2) (m-n):2; 3) -2(m-n); 4) m-n-2,1.
Решение:а) Т.к. s-t=-1,3,то t-s=1,3. 1) (t-s)2=1,32=1,69; 2) (t-s):2=1,3:2=0,65; 3) 2(t-s)=2×1,3=2,6; 4) s-t-1,3=-1,3-1,3=-2,6.Ответ: 3).
3. Разложите на множители квадратный трехчлен:а) х2-7х+10;б)
х2-10х+16.
Решение:а) Найдем дискриминант: D=49-40=9. Вычислим корни: x1=(7+3):2=5; x2=(7-3):2=2.Тогда х2-7х+10=(х-5)(х-2).Ответ: (х-5)(х-2).
4. Сократите дробь:
Решение:а) В числителе вынесем за скобки общий множитель 9b:
5. Сократите дробь:
Решение:
а) В числите воспользуемся формулой разности квадратов, в знаменателе вынесем общий множитель 3 за скобки.
6. Упростите выражение:
Решение:
а)
7. Разложите многочлен на множители:
а) 2x+4y-xy-2y2; б) xy-6x+3y-2×2.
Решение:а) Сгруппируем первое со вторым слагаемые и третье с четвертым:2x+4y-xy-2y2=(2x+4y)+(-xy-2y2)=2(x+2y)-y(x+2y)=(x+2y)(2-y).Ответ: (х+2у)(2-у).
8. Найдите, при каких значениях переменной не имеет смысла выражение:
Решение:а) Выражение не имеет смысла, если знаменатель равен нулю. Найдем значения переменной х, при которых a2-16a равно нулю:a2-16a=0,а(а-16)=0,а=0 или а-16=0,а+0 или а=16.Ответ: 0; 16.
9. Сократите дробь:
Решение:а) Вынесем в числителе общий множитель а за скобки, в знаменателе за скобки вынесем общий множитель b:
10. Сократите дробь:
Решение:
11. Разложите на множители:
а)2х2-20ху+50у2-2; б)3х2+12у2+12ху-12.
Решение:а) Вынесем общий множитель 2 за скобки, затем воспользуемся формулой квадрата разности и формулой разности квадратов: 2х2-20ху+50у2-2=2(x2-10xy+25y2-1)=2((x-5y)2-1)=2(x-5y-1)(x-5y+1). Ответ: 2(x-5y-1)(x-5y+1).
12. Сократите дробь (№ 2/4/17 :
Решение:
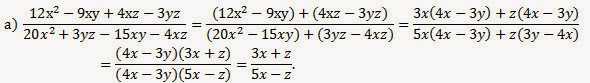
13. Упростите выражение:
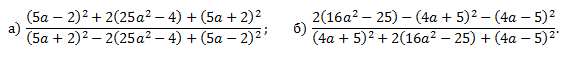Решение:а) 2(25a2-4) можно представить в виде 2(5а-2)(5а+2), тогда в числителе воспользуемся формулой квадрата суммы, а в знаменателе — квадрата разности:
14. а) Первое натуральное число при делении на 5 дает остаток 2, а другое — остаток 3. Найдите, какой остаток получится при делении на 5 удвоенного произведения этих чисел. б) Первое натуральное число при делении на 9 дает остаток 6, а другое — остаток 1. Найдите, какой остаток получится при делении на 9 произведения суммы и разности этих чисел.
Решение:а) Обозначим первое число х, тогда используя формулу деления с остатком его можно записать следующим образом: х=5b+2. Обозначим второе число у, по формуле деления с остатком у=5а+3. Найдем удвоенное произведение этих чисел:2ху=2(5b+2)(5a+3)=(10b+4)(5a+3)=50ab+30b+20a+12=5(10ab+6b+4a+2)+2.Мы представили удвоенное произведение в виде формулы деления с остатком на 5, следовательно остаток равен 2.Ответ: 2.
15. Найдите х из пропорции (№ 2.5.28 :
Решение:а) Преобразуем числитель первой дроби: 25-n2-2mn-m2=25-( n2 +2mn+m2)=52-(n+m)2=(5-(n+m))(5+(n+m))=(5-n-m)(5+n+m).Преобразуем знаменатель первой дроби:
n2+nm+5m-25=(n2
-25)+(nm+5m)=(n-5)(n+5)+m(n+5)=(n+5)(n-5+m).
Подставим в пропорцию результаты, которые получили:
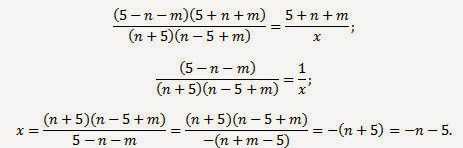
Куб суммы и куб разности
\( \displaystyle {{(a+b)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\)
Формулы куба суммы и куба разности выводятся аналогичным образом, как квадрат суммы и квадрат разности: раскрытием скобок при перемножении членов друг на друга.
Если квадрат суммы и квадрат разности запомнить весьма легко, то возникает вопрос «как запомнить кубы?»
Посмотри внимательно на две описываемые формулы в сравнении с возведением аналогичных членов в квадрат:
| \( {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\) | \( {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\) |
| \( {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\) | \( {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\) |
Какую ты видишь закономерность?
- При возведении в квадрат у нас есть квадрат первого числа и квадрат второго. При возведении в куб – есть куб одного числа и куб другого числа.
- При возведении в квадрат, у нас есть удвоенное произведение чисел (числа в 1 степени, что на одну степень меньше чем та, в которую возводим выражение). При возведении в куб – утроенное произведение, при котором одно из чисел возводится в квадрат (что так же на 1 степень меньше, чем степень, в которую возводим выражение).
- При возведении в квадрат знак в скобках в раскрытом выражении отражается при прибавлении (или вычитании) удвоенного произведения – если в скобках сложение, то прибавляем, если вычитание – отнимаем. При возведении в куб правило такое: если у нас куб суммы, то все знаки «+», а если куб разности, то знаки чередуются: «\( +\)» — «\( —\)» — «\( +\)» — «\( —\)».
Всё перечисленное, кроме зависимости степеней при умножении членов, изображено на рисунке.
Применение формул сокращенного умножения
Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.
- a2 + 2a + 1 = (a + 1)2
- (aс − 4b)(ac + 4b) = a2c2 − 16b2
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители:
вынесение общего множителя за скобки и
способ группировки.
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.
Вспомним, как выглядит формула разности кубов.
Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.
Важно понимать, что любая формула сокращённого умножения действует и в. (a − b)(a2 ab + b2) = a3 − b3
(a − b)(a2 ab + b2) = a3 − b3
Как разложить на множители разность кубов
Рассмотрим пример. Необходимо разложить на множители разность кубов.
Обратим внимание, что «» — это «», значит, для формулы разности кубов вместо «» мы используем «». Используем формулу разности кубов
На месте «» у нас стоит «», а на месте «», как и в формуле, стоит «»
Используем формулу разности кубов. На месте «» у нас стоит «», а на месте «», как и в формуле, стоит «».
Применение разности кубов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.
Обратите внимание, что произведение многочленов «(x − 1)(x2 + x + 1)» напоминает правую часть формулы разности кубов
«a3 − b3 = (a − b)(a2 ab + b2)», только вместо «» стоит «», а на месте «» стоит «».
Используем для «(x − 1)(x2 + x + 1)» формулу разности кубов в обратную сторону.
Рассмотрим пример сложнее. Требуется упростить произведение многочленов.
Если сравнить «(y2 − 1)(y4 + y2 + 1)» с правой частью формулы разности кубов «a3 − b3 = (a − b)(a2 ab + b2)», то можно понять, что на месте «» из первой скобки стоит «, а на месте «» стоит «».
Одночлены, которые стоят на месте «» или «» могут стоять в степени.
Например, в рассматриваемом примере на месте «» стоит «». Это означает, что именно «» мы рассматриваем как «».
Представим скобку «(y4 + y2 + 1)» таким образом, чтобы она соответствовала правой части формулы разности кубов.
Используем формулу разности кубов и решим пример до конца.
Вспомним, как выглядит формула суммы кубов.
a3 + b3 = (a + b)(a2 ab + b2)
Формула суммы кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.
(a + b)(a2 ab + b2) = a3 + b3
Как разложить на множители сумму кубов
Рассмотрим пример. Необходимо разложить на множители сумму кубов.
Обратим внимание, что «» — это «», значит, для формулы суммы кубов вместо «» мы используем «». Используем формулу суммы кубов
Только вместо «» у нас будет «», а вместо «» будет «»
Используем формулу суммы кубов. Только вместо «» у нас будет «», а вместо «» будет «».
Применение суммы кубов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов в сумму кубов, используя формулу сокращенного умножения.
Обратите внимание, что произведение многочленов «(p + 1)(p2 − p + 1)» напоминает правую часть формулы суммы кубов
«a3 + b3 = (a + b)(a2 ab + b2)», только вместо «» стоит «», а на месте «» стоит «».
Используем для произведения многочленов «(p + 1)(p2 − p + 1)» формулу сумму кубов в обратную сторону.
В этом произведении многочленов не так очевидно, что будет являться в формуле «», а что «».
Если сравнить «(2a + 3)(4a2 − 6a + 9)» с формулы суммы кубов «a3 + b3 = (a + b)(a2 ab + b2), то можно понять, что в первой скобке «(2a + 3)» на месте «» стоит «», а на месте «» стоит «».
Теперь представим скобку «(4a2 − 6a + 9)» таким образом, чтобы она соответствовала правой части формулы суммы кубов.
Используем формулу суммы кубов и решим пример до конца.
В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, разложение разности кубов на множители. Также разберем примеры решения задач для закрепления представленного материала.
Квадрат суммы
\( \displaystyle {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\)
Название «Формулы сокращенного умножения» совсем не случайно, потому что эти формулы позволяют сократить время на умножение. Вот смотри…
Возьмем самую простую первую формулу квадрата суммы \( {{\left( a+b \right)}^{2}}\) — и попробуем возвести сумму в скобках в квадрат, то есть, умножить \( \left( a+b \right)\) само на себя:
Приведи подобные слагаемые и ты получишь формулу сокращенного умножения квадрат суммы:
Таким образом выводятся все формулы сокращенного умножения.
Ты можешь выводить их каждый раз самостоятельно, а можешь не тратить на это время и быстро посчитать необходимый пример, зная конечное значение формул.
Конечно, квадрат суммы посчитать вручную не так сложно, но что ты скажешь насчет куба суммы или куба разности?
Куб суммы означает, что необходимо \( \left( a+b \right)\) само умножить на себя три раза:
И это мы расписали перемножение только первой скобки, а тоже самое необходимо сделать со второй и с третьей… Согласись, запутаться очень легко, а, как правило, от того, как ты посчитаешь это простое действие, зависит ответ всего примера.
Таким образом, формулы сокращенного умножения позволяют сократить трудоемкое перемножение членов друг на друга и получить быстрый результат.
Куб суммы и куб разности
Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Формулу куба суммы двух выражений можно прочитать так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
А формулу куба разности двух выражений можно прочитать так:
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.
Выведем формулу куба суммы самостоятельно:
(a + b)3
Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)
(a + b)3 = (a + b)(a + b)(a + b)
Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2
(a + b)3 = (a + b)(a + b)2
При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.
Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).
(a + b)3 = (a + b)(a2 + 2ab + b2)
А это есть умножение многочлена на многочлен. Выполним его:
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Аналогично можно вывести формулу куба разности двух выражений:
(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3×2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2×2 + x + x2 + 2x + 1 = x3 + 3×2 + 3x + 1
Пример 2. Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(6a2 + 3b3)3= (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9
Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Пример 4. Преобразовать выражение (2×2 − x3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(2×2 − x3)3 = (2×2)3 − 3 × (2×2)2 × x3 + 3 × 2×2 × (x3)2 − (x3)3 =8×6 − 3 × 4×4 × x3 + 3 × 2×2 × x6 − x9 =8×6 − 12×7 + 6×8 − x9