Определение степени с натуральным показателем

Действия со степенями: правила вычисления степеней с разными основаниями или натуральными показателями по математике и порядок этого

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.

В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.

Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.

Что такое степень числа

Что же подразумевают под выражением «возвести число в степень»?

Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом: an = a * a * a * …an.

Причем, левая часть уравнения будет читаться, как a в степ. n.

Например:

• 23 = 2 в третьей степ. = 2 * 2 * 2 = 8,
• 42 = 4 в степ. два = 4 * 4 = 16,
• 54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625,
• 105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000,
• 104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.

Ниже будет представлена таблица квадратов и кубов от 1 до 10.

Таблица степеней от 1 до 10

Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».

Ч-ло	2-ая ст-нь	3-я ст-нь
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

• an * am = (a)(n+m),
• an : am = (a)(n-m),
• (ab ) m=(a)(b*m).

Проверим на примерах:

23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.

Аналогично:

• 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
• (23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

33 + 24 = 27 + 16 = 43,
52 – 32 = 25 – 9 = 16

Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.. Как производить вычисления в более сложных случаях? Порядок тот же:. Как производить вычисления в более сложных случаях? Порядок тот же:

Как производить вычисления в более сложных случаях? Порядок тот же:

• при наличии скобок – начинать нужно с них,
• затем возведение в степень,
• потом выполнять действия умножения, деления,
• после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

1. Корень n-ой степени из числа a в степени m запишется в виде: am/n.
2. При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
3. При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
4. При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
5. Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
6. Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Степень с отрицательным показателем

Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5 (смотри пункт выше), получается:

A(-n) = 1 / An, 5(-2) = 1 / 52 = 1 / 25.

И наоборот:

1 / A(-n) = An, 1 / 2(-3) = 23 = 8.

А если дробь?

(A / B)(-n) = (B / A)n, (3 / 5)(-2) = (5 / 3)2 = 25 / 9.

Степень с натуральным показателем

Под ней понимают степень с показателями, равными целым числам.

Что нужно запомнить:

• A0 = 1, 10 = 1, 20 = 1, 3.150 = 1, (-4)0 = 1… и т. д.
• A1 = A, 11 = 1, 21 = 2, 31 = 3 … и т. д.

Кроме того, если (-a)2n+2, n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот. Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.

Урок и презентация на тему: «Степень с отрицательным показателем. Определение и примеры решения задач»

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Определение степени с отрицательным показателем

Мы хорошо знаем, что любое число в нулевой степени равно единице. $a^0=1$, $a≠0$.
Возникает вопрос, а что будет, если возвести число в отрицательную степень? Например, чему будет равно число $2^{-2}$?
Первые математики, задавшиеся этим вопросом, решили, что изобретать велосипед заново не стоит, и хорошо, чтобы все свойства степеней оставались прежними. То есть при умножении степеней с одинаковым основанием, показатели степени складываются.
Давайте рассмотрим такой случай: $2^3*2^{-3}=2^{3-3}=2^0=1$.
Получили, что произведение таких чисел должно давать единицу. Единица в произведении получается при перемножении обратных чисел, то есть $2^{-3}=\frac{1}{2^3}$.

Такие рассуждения привели к следующему определению.
Определение. Если $n$ – натуральное число и $а≠0$, то выполняется равенство:
$a^{-n}=\frac{1}{a^n}$.

Важное тождество, которое часто используется: $(\frac{a}{b})^{-n}=(\frac{b}{a})^n$.
В частности, $(\frac{1}{a})^{-n}=a^n$

Примеры решения

Решение. Рассмотрим каждое слагаемое по отдельности.
1. $2^{-3}=\frac{1}{2^3}=\frac{1}{2*2*2}=\frac{1}{8}$.
2. $(\frac{2}{5})^{-2}=(\frac{5}{2})^2=\frac{5^2}{2^2}=\frac{25}{4}$.
3. $8^{-1}=\frac{1}{8}$.
Осталось выполнить операции сложения и вычитания: $\frac{1}{8}+\frac{25}{4}-\frac{1}{8}=\frac{25}{4}=6\frac{1}{4}$.
Ответ: $6\frac{1}{4}$.

Пример 2. Представить заданное число в виде степени простого числа
$\frac{1}{729}$.

Решение. Очевидно, что $\frac{1}{729}=729^{-1}$.
Но 729 — не простое число, заканчивающиеся на 9. Можно предположить, что это число является степенью тройки. Последовательно разделим 729 на 3.
1) $\frac{729}{3}=243$; 2) $\frac{243}{3}=81$; 3) $\frac{81}{3}=27$; 4) $\frac{27}{3}=9$; 5) $\frac{9}{3}=3$; 6) $\frac{3}{3}=1$.
Выполнено шесть операций и значит: $729=3^6$.
Для нашей задачи:
$729^{-1}=(3^6)^{-1}=3^{-6}$.
Ответ: $3^{-6}$.

Пример 3. Представьте выражение в виде степени:
$\frac{a^6*(a^{-5})^2}{(a^{-3}*a^8)^{-1}}$.
Решение. Первое действие выполняется всегда внутри скобок, затем умножение
$\frac{a^6*(a^{-5})^2}{(a^{-3}*a^8)^{-1}}=\frac{a^6*a^{-10}}{(a^5)^{-1}}=\frac{a^{(-4)}}{a^{(-5)}}=a^{-4-(-5)}=a^{-4+5}=a$.
Ответ: $a$.

Пример 4. Докажите тождество:
$(\frac{y^2 (xy^{-1}-1)^2}{x(1+x^{-1}y)^2}*\frac{y^2(x^{-2}+y^{-2})}{x(xy^{-1}+x^{-1}y)}):\frac{1-x^{-1} y}{xy^{-1}+1}=\frac{x-y}{x+y}$.

Решение.
В левой части рассмотрим каждый сомножитель в скобках отдельно.
1.
$\frac{y^2(xy^{-1}-1)^2}{x(1+x^{-1}y)^2}=\frac{y^2(\frac{x}{y}-1)^2}{x(1+\frac{y}{x})^2}
=\frac{y^2(\frac{x^2}{y^2}-2\frac{x}{y}+1)}{x(1+2\frac{y}{x}+\frac{y^2}{x^2})}=\frac{x^2-2xy+y^2}{x+2y+\frac{y^2}{x}}=\frac{x^2-2xy+y^2}{\frac{x^2+2xy+y^2}{x}}=\frac{x(x^2-2xy+y^2)}{(x^2+2xy+y^2)}$.
2. $\frac{y^2(x^{-2}+y^{-2})}{x(xy^{-1}+x^{-1}y)}=\frac{y^2(\frac{1}{x^2}+\frac{1}{y^2})}{x(\frac{x}{y}+\frac{y}{x})}
=\frac{\frac{y^2}{x^2}+1}{\frac{x^2}{y}+y}=\frac{\frac{y^2+x^2}{x^2}}{{\frac{x^2+y^2}{y}}}=\frac{y^2+x^2}{x^2} *\frac{y}{x^2+y^2}=\frac{y}{x^2}$.
3. $\frac{x(x^2-2xy+y^2)}{(x^2+2xy+y^2)}*\frac{y}{x^2}=\frac{y(x^2-2xy+y^2)}{x(x^2+2xy+y^2)}=\frac{y(x-y)^2}{x(x+y)^2}$.
4. Перейдем к дроби, на которую делим.
$\frac{1-x^{-1}y}{xy^{-1}+1}=\frac{1-\frac{y}{x}}{\frac{x}{y}+1}=\frac{\frac{x-y}{x}}{\frac{x+y}{y}}=\frac{x-y}{x}*\frac{y}{x+y}=\frac{y(x-y)}{x(x+y)}$.
5. Выполним деление.
$\frac{y(x-y)^2}{x(x+y)^2}:\frac{y(x-y)}{x(x+y)}=\frac{y(x-y)^2}{x(x+y)^2}*\frac{x(x+y)}{y(x-y)}=\frac{x-y}{x+y}$.
Получили верное тождество, что и требовалось доказать.

В конце урока еще раз запишем правила действий со степенями, здесь показатель степени — это целое число.
$a^s*a^t=a^{s+t}$.
$\frac{a^s}{a^t}=a^{s-t}$.
$(a^s)^t=a^{st}$.
$(ab)^s=a^s*b^s$.
$(\frac{a}{b})^s=\frac{a^s}{b^s}$.

Задачи для самостоятельного решения

В этой статье мы разберемся, что такое степень числа
. Здесь мы дадим определения степени числа, при этом подробно рассмотрим все возможные показатели степени, начиная с натурального показателя, заканчивая иррациональным. В материале Вы найдете массу примеров степеней, покрывающих все возникающие тонкости.

Навигация по странице.

Таблица примеров

Проверьте на рабочем листе книги Excel следующие примеры. Чтобы все заработало корректно, вам необходимо использовать смешанную ссылку при копировании формулы. Закрепите номер столбца, содержащего возводимое число, и номер строки, содержащей показатель. Ваша формула должна иметь примерно следующий вид: «=$B4^C$3».

Число / Степень

Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях. Не возникает проблем и с возведением любых чисел в целые показатели. А вот возведение отрицательного числа в дробную степень обернется для вас ошибкой, поскольку невозможно выполнить правило, указанное в начале нашей статьи про возведение отрицательных чисел, ведь четность — это характеристика исключительно ЦЕЛОГО числа

А вот возведение отрицательного числа в дробную степень обернется для вас ошибкой, поскольку невозможно выполнить правило, указанное в начале нашей статьи про возведение отрицательных чисел, ведь четность — это характеристика исключительно ЦЕЛОГО числа.

Начальный уровень

Стандартный вид числа.

Очень большие и очень малые числа принято записывать в стандартном виде: a∙10n, где 1≤а  и n  (натуральное или целое) – есть порядок числа, записанного в стандартном виде.

•  Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.
•  Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.
•  Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.

Как возводить в отрицательную степень – числа от 0 до 1

Вспомним, что при возведении числа в промежутке от 0 до 1 в положительную степень, значение уменьшается с возрастанием степени. Так например, 0,5 2 = 0,25. 0,25

Пример 3: Вычислить 0,5 -2
Решение: 0,5 -2 = 1/1/2 -2 = 1/1/4 = 1×4/1 = 4.
Ответ: 0,5 -2 = 4

Разбор (последовательность действий):

Переводим десятичную дробь 0,5 в дробную 1/2. Так легче.
Возводим 1/2 в отрицательную степень. 1/(2) -2 . Делим 1 на 1/(2) 2 , получаем 1/(1/2) 2 => 1/1/4 = 4

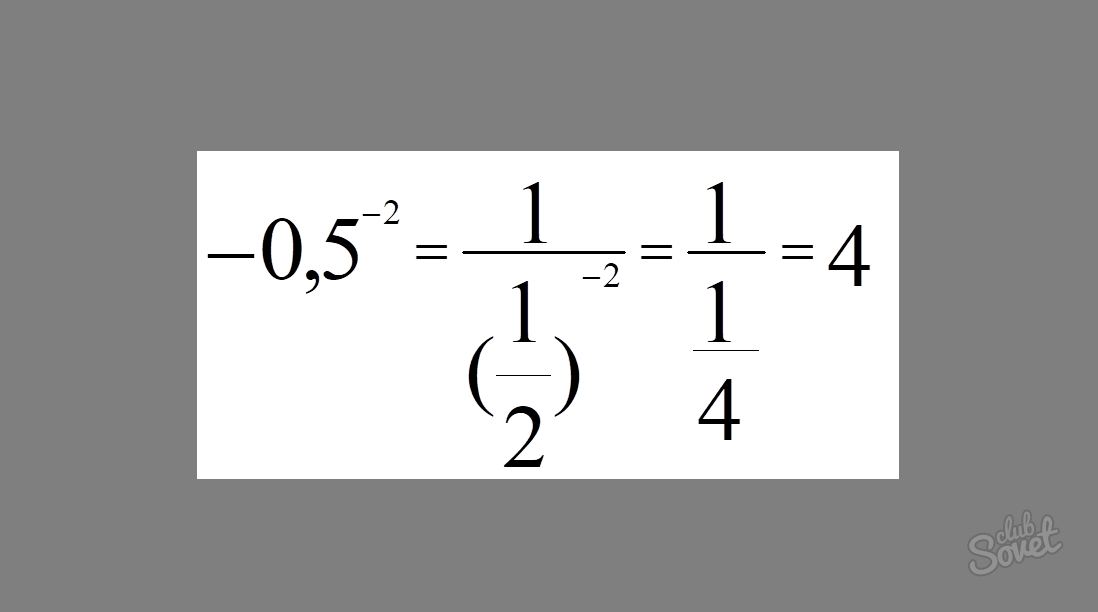
Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8

Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8

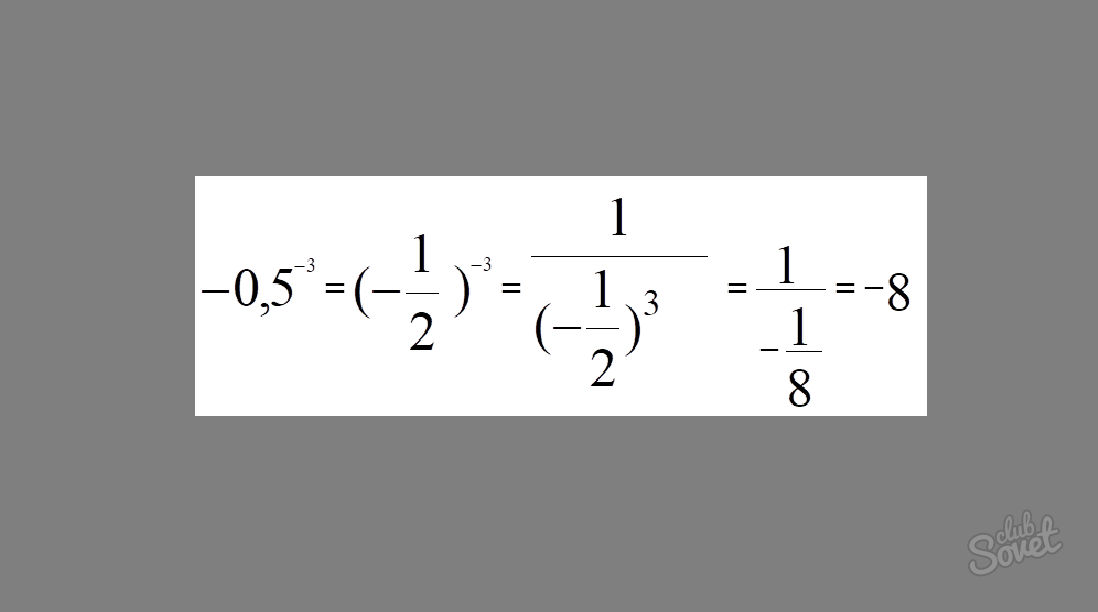
Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:

• Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным. При этом, чем больше степень, тем больше значение.
• Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным. При этом, чем больше степень, тем меньше значение.

Преобразование дробей, содержащих степени

Степенные выражения могут содержать дроби со степенями или представлять собой такие дроби. К таким дробям в полной мере применимы любые из основных преобразований дробей, которые присущи дробям любого вида. То есть, дроби, которые содержат степени, можно сокращать, приводить к новому знаменателю, работать отдельно с их числителем и отдельно со знаменателем и т.д. Для иллюстрации сказанных слов рассмотрим решения нескольких примеров.

Пример.

Упростить степенное выражение .

Решение.

Данное степенное выражение представляет собой дробь. Поработаем с ее числителем и знаменателем. В числителе раскроем скобки и упростим полученное после этого выражение, используя свойства степеней, а в знаменателе приведем подобные слагаемые: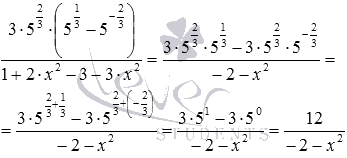

И еще изменим знак знаменателя, поместив минус перед дробью: .

Ответ:

Приведение содержащих степени дробей к новому знаменателю проводится аналогично приведению к новому знаменателю рациональных дробей. При этом также находится дополнительный множитель и выполняется умножение на него числителя и знаменателя дроби. Выполняя это действие, стоит помнить, что приведение к новому знаменателю может приводить к сужению ОДЗ. Чтобы этого не происходило, нужно, чтобы дополнительный множитель не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример.

Приведите дроби к новому знаменателю: а) к знаменателю a, б) к знаменателю .

Решение.

а) В этом случае довольно просто сообразить, какой дополнительный множитель помогает достичь нужного результата. Это множитель a0,3, так как a0,7·a0,3=a0,7+0,3=a. Заметим, что на области допустимых значений переменной a (это есть множество всех положительных действительных чисел) степень a0,3 не обращается в нуль, поэтому, мы имеем право выполнить умножение числителя и знаменателя заданной дроби на этот дополнительный множитель:

б) Присмотревшись повнимательнее к знаменателю, можно обнаружить, что
и умножение этого выражения на даст сумму кубов и , то есть, . А это и есть новый знаменатель, к которому нам нужно привести исходную дробь.

Так мы нашли дополнительный множитель . На области допустимых значений переменных x и y выражение не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:

Ответ:

а) , б) .

В сокращении дробей, содержащих степени, также нет ничего нового: числитель и знаменатель представляются в виде некоторого количества множителей, и сокращаются одинаковые множители числителя и знаменателя.

Пример.

Сократите дробь: а) , б) .

Решение.

а) Во-первых, числитель и знаменатель можно сократить на наибольший общий делитель (НОД) чисел 30 и 45, который равен 15. Также, очевидно, можно выполнить сокращение на x0,5+1 и на . Вот что мы имеем:

б) В этом случае одинаковых множителей в числителе и знаменателе сразу не видно. Чтобы получить их, придется выполнить предварительные преобразования. В данном случае они заключаются в разложении знаменателя на множители по формуле разности квадратов:

Ответ:

а)
б) .

Приведение дробей к новому знаменателю и сокращение дробей в основном используется для выполнения действий с дробями. Действия выполняются по известным правилам. При сложении (вычитании) дробей, они приводятся к общему знаменателю, после чего складываются (вычитаются) числители, а знаменатель остается прежним. В результате получается дробь, числитель которой есть произведение числителей, а знаменатель – произведение знаменателей. Деление на дробь есть умножение на дробь, обратную ей.

Пример.

Выполните действия .

Решение.

Сначала выполняем вычитание дробей, находящихся в скобках. Для этого приводим их к общему знаменателю, который есть , после чего вычитаем числители:

Теперь умножаем дроби:

Очевидно, возможно сокращение на степень x1/2, после которого имеем .

Еще можно упростить степенное выражение в знаменателе, воспользовавшись формулой разность квадратов: .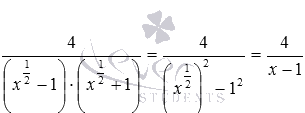

Ответ:

Пример.

Упростите степенное выражение .

Решение.

Очевидно, данную дробь можно сократить на (x2,7+1)2, это дает дробь . Понятно, что надо еще что-то сделать со степенями икса. Для этого преобразуем полученную дробь в произведение . Это дает нам возможность воспользоваться свойством деления степеней с одинаковыми основаниями: 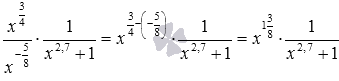. И в заключение процесса переходим от последнего произведения к дроби .

Ответ:

И еще добавим, что можно и во многих случаях желательно множители с отрицательными показателями степени переносить из числителя в знаменатель или из знаменателя в числитель, изменяя знак показателя. Такие преобразования часто упрощают дальнейшие действия. Например, степенное выражение можно заменить на .

Свойства степеней с целыми показателями

Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.

, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.

Итак, для любых действительных и отличных от нуля чисел a и b, а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями:

1. am·an=am+n;
2. am:an=am−n;
3. (a·b)n=an·bn;
4. (a:b)n=an:bn;
5. (am)n=am·n;
6. если n – целое положительное число, a и b – положительные числа, причем a<b, то an<bn и a−n>b−n;
7. если m и n – целые числа, причем m>n, то при 0<a<1 справедливо неравенство am<an, а при a>1 выполняется неравенство am>an.

При a=0 степени am и an имеют смысл лишь когда и m, и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0, а числа m и n – целые положительные.

Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q). Сделаем это.

Для положительных p и q равенство (ap)q=ap·q доказано в предыдущем пункте. Если p=0, то имеем (a)q=1q=1 и a0·q=a=1, откуда (a)q=a0·q. Аналогично, если q=0, то (ap)=1 и ap·0=a=1, откуда (ap)=ap·0. Если же и p=0 и q=0, то (a)=1=1 и a0·0=a=1, откуда (a)=a0·0.

Теперь докажем, что (a−p)q=a(−p)·q. По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1p=1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a−(p·q), которую в силу правил умножения можно записать как a(−p)·q.

Аналогично .

И .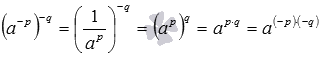

По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.

В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a−n>b−n, которое справедливо для любого целого отрицательного −n и любых положительных a и b, для которых выполняется условие a<b. Доказываемое неравенство по определению степени с целым отрицательным показателем можно переписать как . Запишем и преобразуем разность левой и правой частей этого неравенства: . Так как по условию a<b, то по свойству степени с натуральным показателем an<bn, следовательно, bn−an>0. Произведение an·bn тоже положительно как произведение положительных чисел an и bn. Тогда полученная дробь положительна как частное положительных чисел bn−an и an·bn. Следовательно, откуда a−n>b−n, что и требовалось доказать.

Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Пример 12

Представьте выражение x 1 9 · x · x 3 6 в виде степени.

Решение

Область допустимых значений переменной x
определяется двумя неравенствами x ≥ 0
и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞)
.

На этом множестве мы имеем право перейти от корней к степеням:

x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6

Используя свойства степеней, упростим полученное степенное выражение.

x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3

Ответ:
x 1 9 · x · x 3 6 = x 1 3 .

Умножение степеней с разными основаниями

Как умножить степени с разными основаниями и показателями? Умножение степеней с разными основаниями возможно, если основания степеней одинаковые. В этом случае нужно сложить показатели степеней и оставить основание неизменным. Например, если нужно умножить две степени x^4 и x^3, где основания одинаковые (x), то результатом будет x^(4+3) = x^7.

Однако, если основания степеней разные, то умножение степеней не производится. Вместо этого, результатом умножения степеней с разными основаниями будет произведение самих степеней. Например, если нужно умножить степени x^2 и y^3, то результатом будет x^2 * y^3.

Также, при умножении степени на степень с разными основаниями, можно применить правило степени степени. Правило гласит: при умножении степени на степень, нужно умножить показатели степеней и оставить основание неизменным. Например, если нужно умножить степень (x^3)^2 на степень (x^2)^3, то результатом будет (x^(3*2)) * (x^(2*3)) = x^6 * x^6 = x^12.

В некоторых случаях, при умножении степеней с разными основаниями, можно использовать таблицу умножения степеней. Таблица позволяет найти правило для умножения степеней оснований при различных показателях. Например, при умножении степеней x^m и y^n, можно использовать таблицу умножения степеней для определения правила x^m * y^n.

Правило умножения степеней с разными основаниями

Умножение степеней с разными основаниями — это операция, при которой необходимо умножить две или более степени с разными основаниями и показателями. Для выполнения этого действия существует определенное правило.

Правило умножения степеней с разными основаниями состоит в следующем: если у нас есть две степени с разными основаниями, то основания необходимо перемножить, а показатели сложить между собой.

Например, чтобы умножить степени 2^3 и 3^4, нужно перемножить их основания, то есть 2 и 3, и сложить показатели, то есть 3 и 4. В итоге получаем степень 6^7.

Правило умножения степеней с разными основаниями можно применять не только к двум, но и к более чем двум степеням. В этом случае основания всех степеней перемножаются, а показатели складываются.

Например, чтобы умножить степени 2^3, 3^4 и 4^2, нужно перемножить их основания 2, 3 и 4, и сложить показатели 3, 4 и 2. В итоге получаем степень 24^9.

Примеры умножения степеней с разными основаниями

Умножение степеней с разными основаниями представляет собой процесс, при котором перемножаются значения, возведенные в степень и имеющие разные основания. Для выполнения такого умножения необходимо учесть и основания, и показатели степеней.

Например, если нужно умножить две степени с разными основаниями, например, 2 в степени 3 и 3 в степени 4, нужно умножить основания (2 и 3) и сложить показатели степеней (3 и 4). Таким образом, получим результат: 2 в степени 3 умножить на 3 в степени 4 равно 2 * 3 в степени 3 + 4, то есть 6 в степени 7.

Еще один пример умножения степеней с разными основаниями: 5 в степени 2 умножить на 4 в степени 3. В данном случае необходимо умножить основания (5 и 4) и сложить показатели степеней (2 и 3). Таким образом, получим результат: 5 в степени 2 умножить на 4 в степени 3 равно 5 * 4 в степени 2 + 3, то есть 20 в степени 5.

Еще одним примером умножения степеней с разными основаниями может быть: 2 в степени 5 умножить на 3 в степени 2 умножить на 4 в степени 3. Здесь нужно умножить основания (2, 3 и 4) и сложить показатели степеней (5, 2 и 3). Таким образом, получим результат: 2 в степени 5 умножить на 3 в степени 2 умножить на 4 в степени 3 равно 2 * 3 * 4 в степени 5 + 2 + 3, то есть 24 в степени 10.

Таким образом, умножение степеней с разными основаниями осуществляется путем умножения оснований и сложения показателей степеней. Результатом является степень, в которой новое основание получается путем перемножения оснований, а показатель равен сумме показателей исходных степеней.

Свойство степени с натуральным показателем и особенности вычисления

Определение

Натуральный показатель степени и его свойства — это, где показателем степени является натуральное, положительное числовое значение.

Натуральный показатель степени имеет следующие свойства:  

а) Главное свойство:  

xnxm =xn+m

ynym =xn+m

Равенство является верным при любых значениях m и n. И действительном значении а. 

(x x …x) — n множителей 

(x x …x) — m множителе 

Равенство мы разберем на конкретном  числовом примере:

Мы имеем две степени с основание четыре.

Натуральные показатели имеют значения три, и пять соответственно. 

Составим равенство, подставляя числовые значения:

43 x45=(4·4·4)(4·4·4·4·4)=64×1024=65536 или 48=4·4·4·4·4·4·4·4=65536

Решив равенство, мы получаем: 4345=48

Тем самым, мы видим, что равенство доказано. 

Также, используя свойство умножения, можно обобщить свойства. Если в равенстве представлены от трех и более степеней. Натуральные числа обозначим m1, m2.

Составим равенство: xm1xm2……xmk

Составим  несколько равенство, подставляя числовые значения, для лучшего усвоения:

(2)2(2)3(2)3(2)4=(2)2+3+3+4=(2)12

(3)2(3)3(3)3(3)4=(3)2+3+3+4=(3)12

(5)2(5)3(5)3(5)4=(5)2+3+3+4=(5)12

б) Свойство частных  степени, когда основания имеют одинаковые значения

Свойство частных имеет следующий вид, в виде равенства:

xnxm =xn-m

Оно справедливо при любых натуральных значений n и m, любом значении x, кроме нуля.  Значение основания, нельзя принимать равным нулю. В противном случае при расчете, придется делить на ноль, что по правилам математики недопустимо. 

Так же, есть еще одно условие: значение n должно быть больше, значения m. После вычета должно получится положительное число.

Для доказательства условия, составим равенство:

xn-mxm=x(n-m)+m=xn

Преобразовав равенство, мы можем вывести следующий пример:

xn-mxm=xn

Для наглядности, подставим числовые значения:

2522=25-3=23

4542=45-3=42

в) Произведение степеней

Степень произведения можно выразить в виде равенства:

(xy)m=xmym

Равенство можно преобразовать в следующей вид:

(xy)m=(xy)(xy)……(xy), количество множителей равно числовому значению степени.

Рассмотрим несколько  равенств с числовыми значениями: 

— Вариант для положительных значений:

(45)3=(4)3(5)3

(58)3=(5)3(8)3 

— Вариант для дробей:

(56×24)4=(56)4(24)4 

— Вариант отрицательных значений:

(56(-89))4=(56)4(-89)4

г) Возведение частного в натуральную степень.

Составим равенство для доказательства данного свойства.

(xy)m=xmym

Должны соблюдаться следующие условия:

• значения x и y, должны быть не равны нулю;
• степень (m) — натуральное число.

Для доказательств равенства распишем пример:

(xy)mym=((xy)y)n=xm

Для закрепления знаний, решим несколько примеров, заменяя буквенные значения числовыми.

(168)2=(16)2(8)2

(12(-7))2=(12)2(-7)2

(1,3(-3))3=(1,3)3(-3)3

(1,4(-3))3=(1,4)3(-3)3

д) Принцип возведения степени в степень

Составим равенство:

(xn)m=xnxm

(25)4=25×4=220

Также, данное свойство, может быть выражено и несколькими степенями, в виде:

((((xn)b)a)m=xn·x·b·a·m

Для решения равенства, такого типа, необходимо перемножить между собой значение степеней.

((((32)3)4)2=32342=348

((((5)3)4)2=52342=548

((((12)3)4)6=32346=3192

е) Принципы равенства и неравенства.

Данный принцип звучит следующим образом: большее значение имеет степень, у  которой значение основания степени большее или наоборот. 

Например:

x2<y2 или подставив числовые значения, образует вид: 45<55

Еще несколько примеров для закрепления, с разными числовыми значениями:

121,5<32 1.5

42>32

32>12

Как видно из примеров, равенство верно, в том случае если значение основания больше.

Принцип неравенства считается верным, если одна степень больше значения другой, а основание больше нуля, но не меньше единицы. То есть, числовое значение должно быть положительным.

xn>xm

45>42

Применение степеней и их свойств

Они активно применяются в алгебре и геометрии

Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять

Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений

Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.

Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.

Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.

Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.

Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.

Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.

С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.

Определение степени

Степень — это математическое понятие, которое позволяет увеличивать или уменьшать число с помощью умножения или деления на основание этой степени. Степень может иметь разные основания и показатели.

Для умножения степеней с разными основаниями и показателями необходимо перемножить основания и сложить показатели. Например, если у нас есть степень a^m и степень b^n, то результатом будет степень (a * b)^(m + n). При этом основания умножаются, а показатели складываются. Это правило справедливо для любых чисел или выражений.

В случае, если у нас есть несколько степеней с одним и тем же основанием, но разными показателями, мы можем перемножить показатели, не изменяя основание. То есть, если у нас есть степени a^m и a^n, где a — это основание, то результатом будет степень a^(m + n). Это правило называется свойством степени с одним и тем же основанием.

Определение степени имеет важное значение в математике и используется во многих областях, включая физику, экономику и программирование. На практике степени помогают упростить выражения, сравнивать и считать большие числа, решать задачи по процентам и многое другое

9 класс

№ урока	Тема
1	Повторение материала 8 класса 11 минут 54секунд
2	Повторение материала 8 класса. Решение систем уравнений 13 минут 57секунд
3	Квадратичная функция.y = ax2 12 минут 11секунд
4	Квадратичная функция y = ax2 + bx + c 14 минут 13секунд
5	Графиком квадратичной функции y = ax2 + bx + c. 14 минут 10секунд
6	Область определения функции 14 минут 11секунд
7	Промежутки возрастания и убывания функции 13 минут 51секунд
8	Чётность и нечётность функции 9 минут 51секунд
9	Неравенства и уравнения содержащие степень 14 минут 43секунд
10	Решение задач 12 минут 56секунд
11	Решение задач 11 минут 36секунд
12	Решение систем уравнений второго порядка. 14 минут 21секунд
13	Решение простейших систем, содержащих вторую степень 11 минут 37секунд
14	Решение простейших систем, содержащих вторую степень. 11 минут 37секунд
15	Различные способы решения систем уравнений. 11 минут 11секунд
16	Решение задач (1). 13 минут 5секунд
17	Решение задач.Закрепление (1). 11 минут 36секунд
18	Решение неравенств и систем неравенств второй степени с одной переменной. 9 минут 35секунд
19	Решение примеров. 17 минут 35секунд
20	Решение практических задач. 19 минут 35секунд
21	Решение квадратных неравенств методом интервалов 17 минут 5секунд
22	Решение примеров 15 минут 11секунд
23	Доказательство простых неравенств 14 минут 4секунд
24	Решение примеров 12 минут 17секунд
25	Решение примеров 11 минут 49секунд
26	Решение практических задач. 8 минут 11секунд
27	Решение практических задач. 9 минут 24секунд
28	Радианная мера угла 10 минут 32секунд
29	Поворот точки вокруг начала координат 14 минут 42секунд
30	Определение синуса. Косинуса. Тангенса и Котангенса угла 14 минут 6секунд
31	Решение примеров 13 минут 15секунд
32	Решение примеров 12 минут 38секунд
33	Зависимость между синусом, косинусом и тангенсом одного и того же аргумента 9 минут 39секунд
34	Решение примеров 12 минут 13секунд
35	Тригонометрические тождества 15 минут 18секунд
36	Радианная мера угла 10 минут 36секунд
37	Синус, косинус, тангенс и котангенс углов а И -а 12 минут 54секунд
38	Формулы сложения 11 минут 22секунд
39	Решение примеров 16 минут 16секунд
40	Синус и косинус двойного угла 16 минут 24секунд
41	Формулы приведения 10 минут 12секунд
42	Сумма и разность синусов. Сумма и разность косинусов 17 минут 20секунд
43	Синус, косинус, тангенс и котангенс углов а и -а 12 минут 44секунд
44	Числовые последовательности 17 минут 0секунд
45	Арифметические прогрессия 11 минут 4секунд
46	Сумма n первых членов арифметической прогрессии 11 минут 53секунд
47	Геометрическая прогрессия 10 минут 45секунд
48	Бесконечно убывающая геометрическая прогрессия 19 минут 29секунд
49	Решение задач 19 минут 29секунд
50	Бесконечно убывающая геометрическая прогрессия 10 минут 17секунд
51	Решение задач 9 минут 35секунд
52	Практические и мепредметные задачи (2 часть) 8 минут 26секунд
53	Решение задач (1 часть) 10 минут 1секунд
54	Решение задач (2 часть) 10 минут 1секунд
55	События 16 минут 3секунд
56	Решение задач 6 минут 30секунд
57	Вероятность события 9 минут 9секунд
58	Решение задач 8 минут 56секунд
59	Относительная частота случайного события 11 минут 40секунд
60	Случайные величины (1) 8 минут 5секунд
61	Случайные величины (2 часть) 8 минут 5секунд
62	Числовые характеристики случайных величин 10 минут 39секунд
63	Решение задач 9 минут 4секунд
64	Повторение 9 минут 58секунд